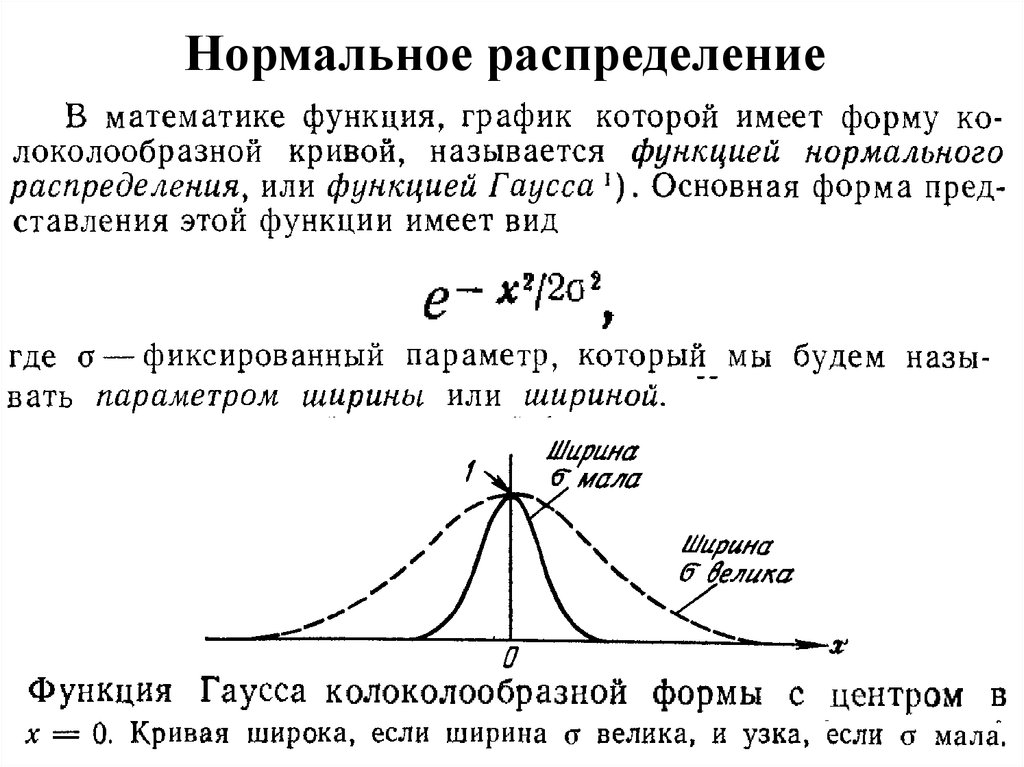
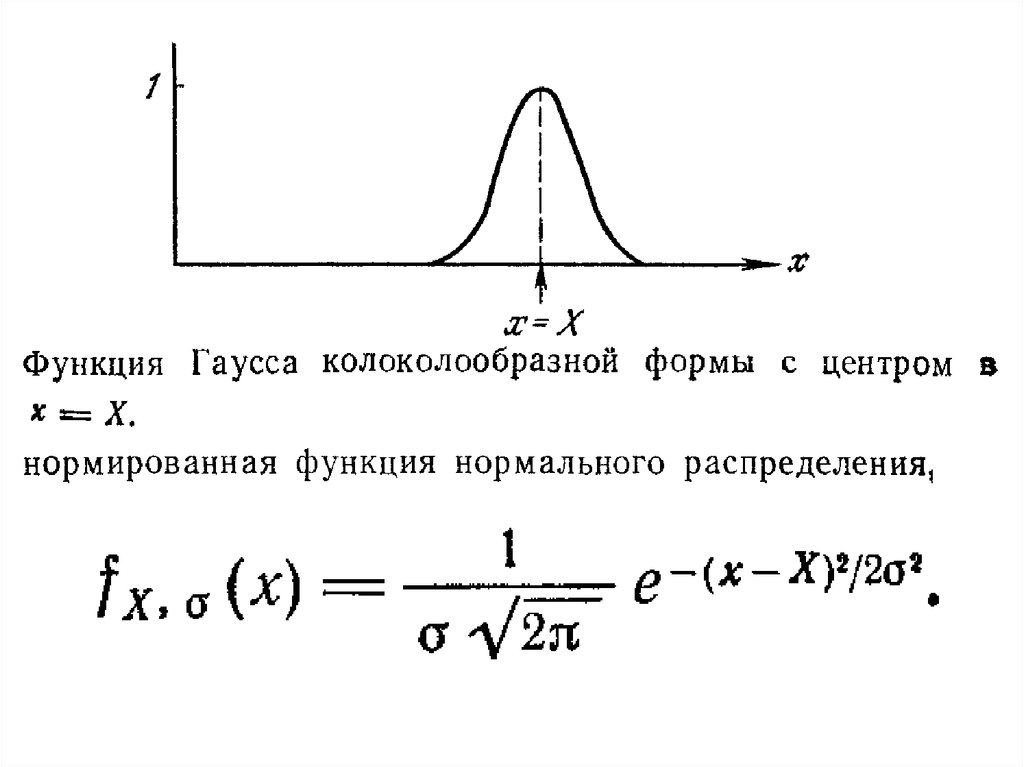
Нормальное распределение

1. Нормальное распределение

2. Гистограммы и распределения

Пусть измерено х (см) – расстояние от линзы до
изображения, создаваемого линзой.

3.

Сумма называется суммой с весовыми
множителями или взвешенной суммой,
поскольку каждое значение xk умножается на
весомый множитель – число nk, показывающее
сколько раз то значение реализовалось.
Если сложим все числа nk, то получим полное
число сделанных измерений.

4.

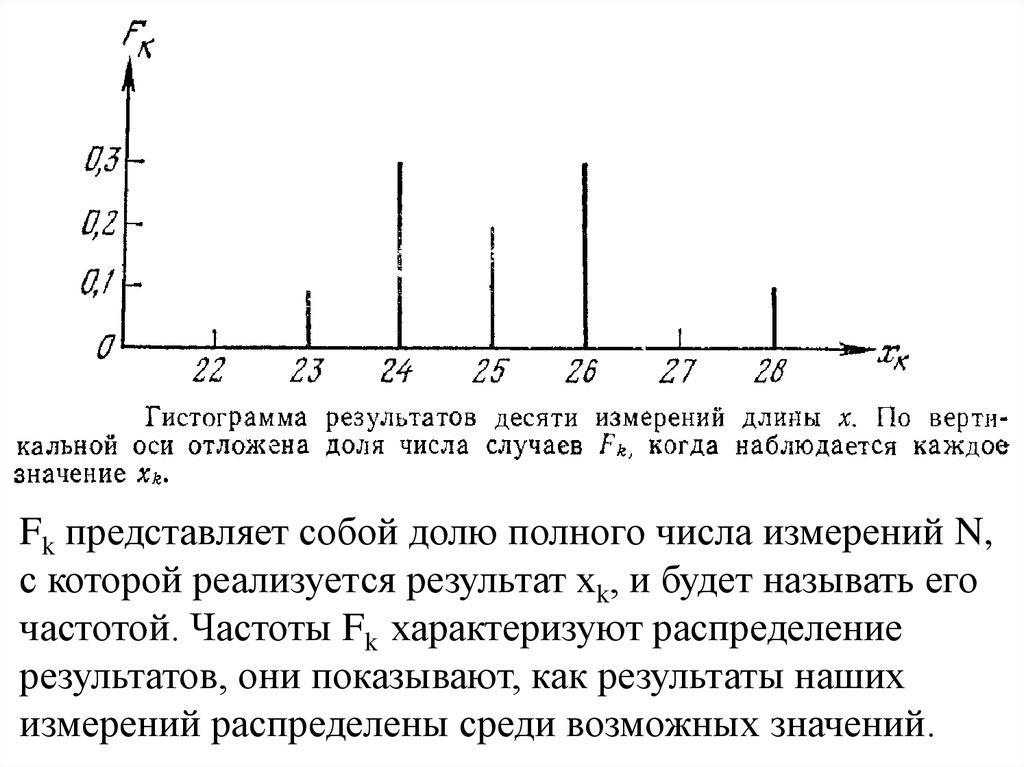
Fk представляет собой долю полного числа измерений N,
с которой реализуется результат хk, и будет называть его
частотой. Частоты Fk характеризуют распределение
результатов, они показывают, как результаты наших
измерений распределены среди возможных значений.

5.

Если сумма какого-то набора чисел равна 1, то эти числа
нормированы, потому то выражение называют условием
нормировки.
Гистограмма может быть названа гистограммой для
дискретной величины, так как распределение результатов
показано высотой вертикальных черточек над
дискретными значениями хk

6.

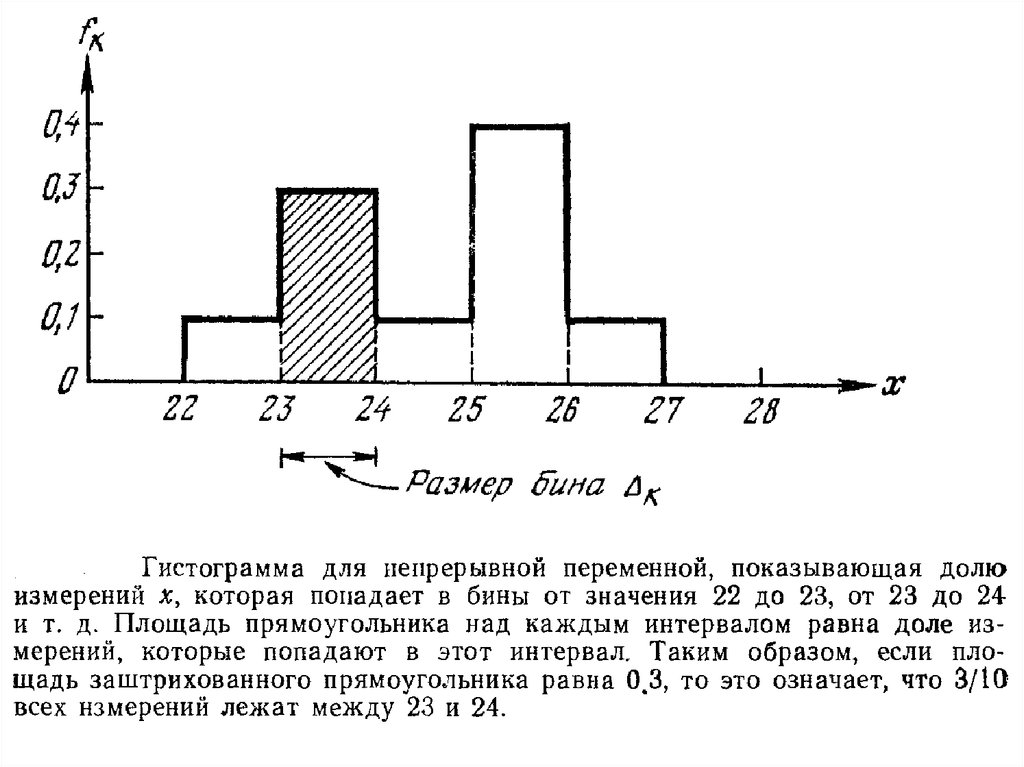
Если результаты измерений – не целые числа, то лучше
всего разбить диапазон возможных значений на
подходящее число интервалов или «бинов», и сосчитать,
сколько значений попадет в каждый бин.

7.

8.

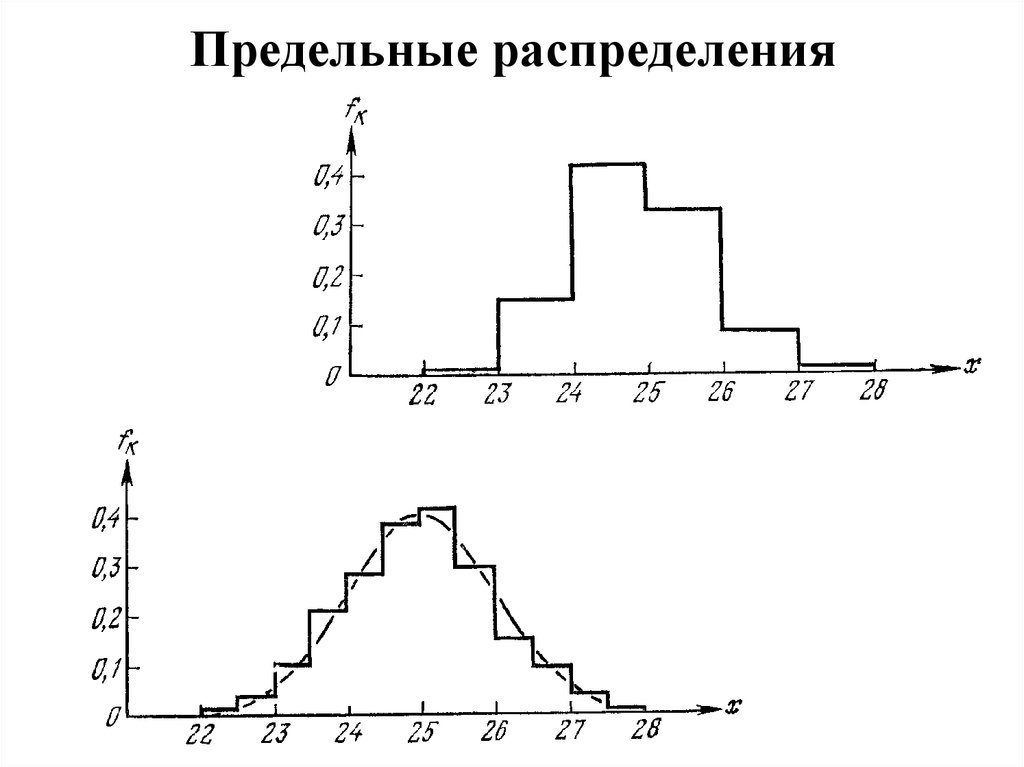
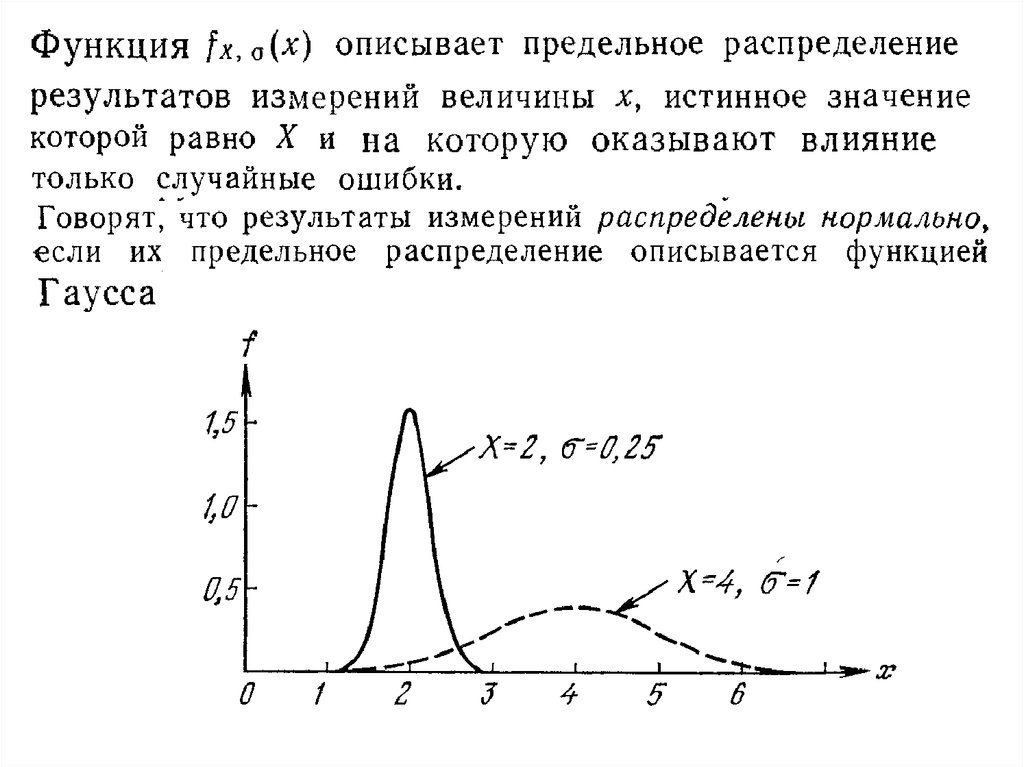
9. Предельные распределения

10.

С ростом числа измерений до бесконечности их
распределение стремится к некоторой определенной
непрерывной кривой. Получающаяся непрерывная
кривая называется предельным распределением.
Почти для всех измерений существует предельное
распределение, к которому гистограмма все более
приближается по мере того, как мы делаем все большее
число измерений.
Предельное распределение, подобное гладкой кривой,
определяет функцию, обозначим f(x).
С ростом числа измерений величины х гистограмма
будет приближаться к предельной кривой. Доля
измерений, которая попадет в любой малый интервал от
х до x+dx будет равна площади f(x)·dx,заштрихованного
участка а)

11.

12.

13.

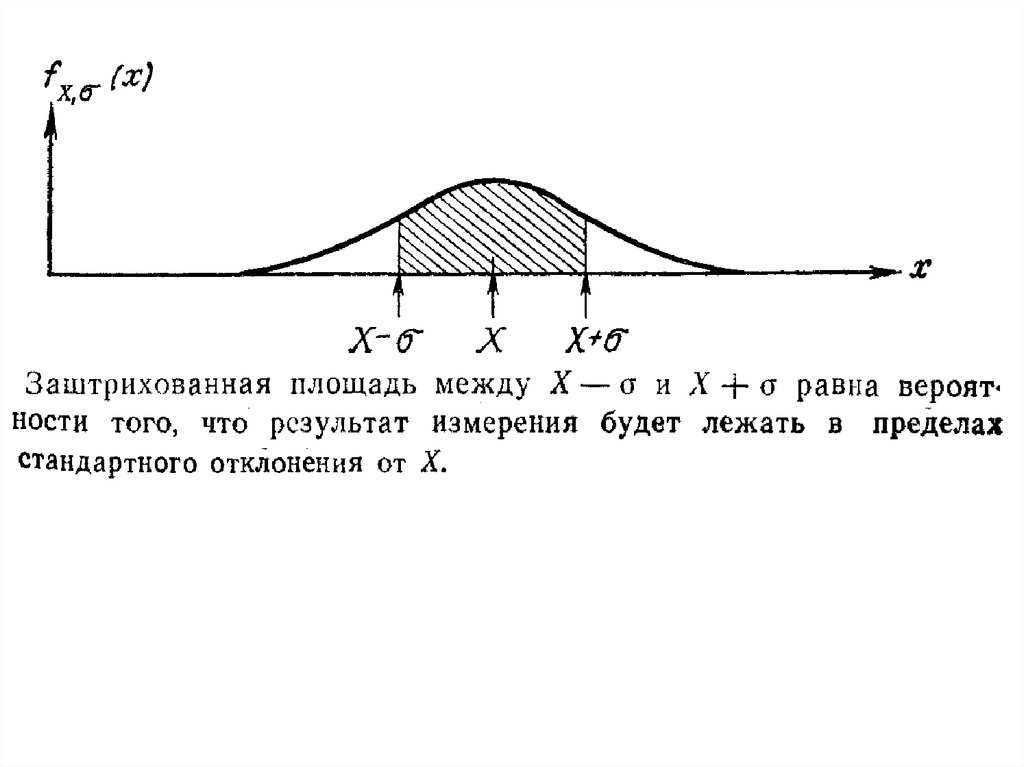
Заключение: если бы нам было известно предельное
распределение f(x) для результатов измерений данной
величины х, полученных с помощью данной
аппаратуры, то мы знали бы вероятность получения
результата в любом заданном интервале a≤x≤b

14.

15.

16.

17. Нормальное распределение