Метаболическая инженерия

1. Метаболическая инженерия

1
Метаболическая инженерия
J. Villadsen, J. Nielsen, G.Liden. Bioreaction engineering principles,
Springer, 2011
E. Klipp, W.Liebermeister, C. Wierling, A.Kowald, H.Lehrach, R.Herwig.
Systems Biology, Wiley-VCH Verlag GmbH & Co. KGaA, 2009.
Безбородов А.М. Ферментативные процессы в биотехнологии / А.М.
Безбородов, Н.А. Загустина, В.О. Попов; Ин-т биохимии им. А.Н. Баха
РАН. – М.: Наука, 2008. – 335 с.
O. Demin, I.Goryanin. Kinetic modeling in Systems Biology, Chapman and
Hall/CRC, 2008.
Бирюков В.В. Основы промышленной биотехнологии. / В.В. Бирюков
М.: КолосС, 2004. – 296 с.
Дж. Бейли, Д. Оллис. Основы биохимической инженерии. Пер с англ. В
2-х частях. Ч. 1. / М.: Мир, 1989. – 692 с.
Дж. Бейли, Д. Оллис. Основы биохимической инженерии. Пер с англ. В
2-х частях. Ч. 2. / М.: Мир, 1989. – 692 с.

2. Управление технологическими режимами периодических и полупериодических процессов

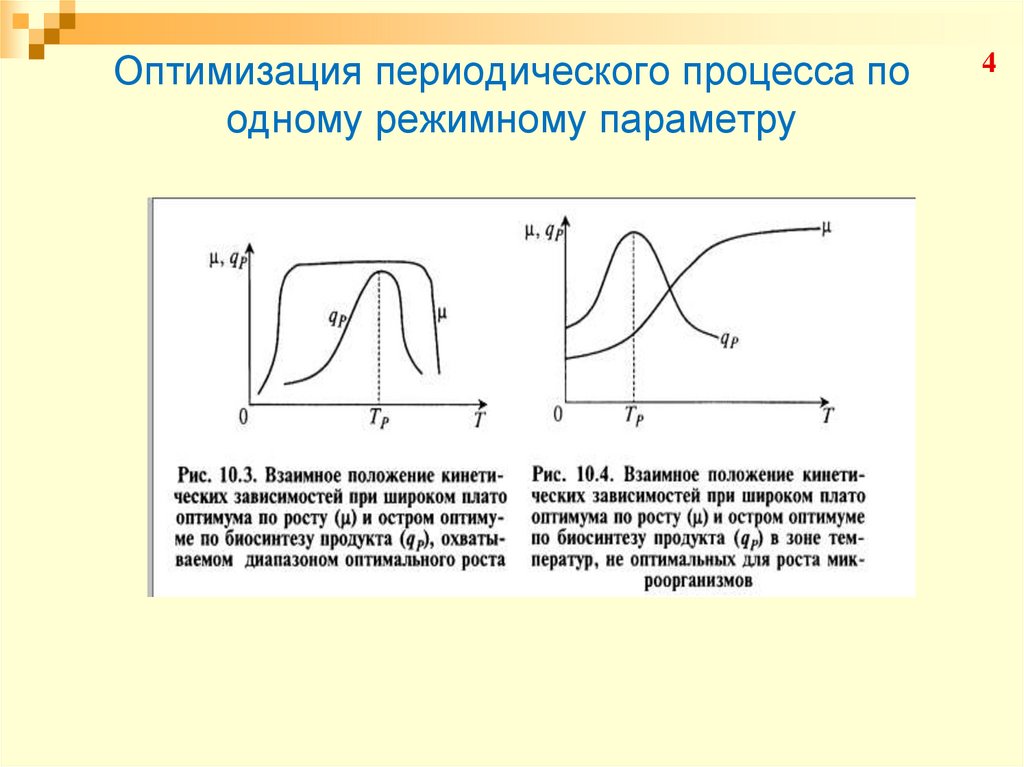
2

3. Оптимизация периодического процесса по одному режимному параметру

3

4. Оптимизация периодического процесса по одному режимному параметру

4

5. Оптимизация периодического процесса по одному режимному параметру

5

6. Оптимизация периодического процесса по одному режимному параметру

Конкординатными называются факторы, для которых
положение оптимума биосинтеза продукта
метаболизма находится в зоне, оптимальной и для
роста биомассы м/о
Дискординатными называются факторы, для которых
оптимум по биосинтезу продуктов метаболизма не
совпадает с оптимумом для роста м/о
6

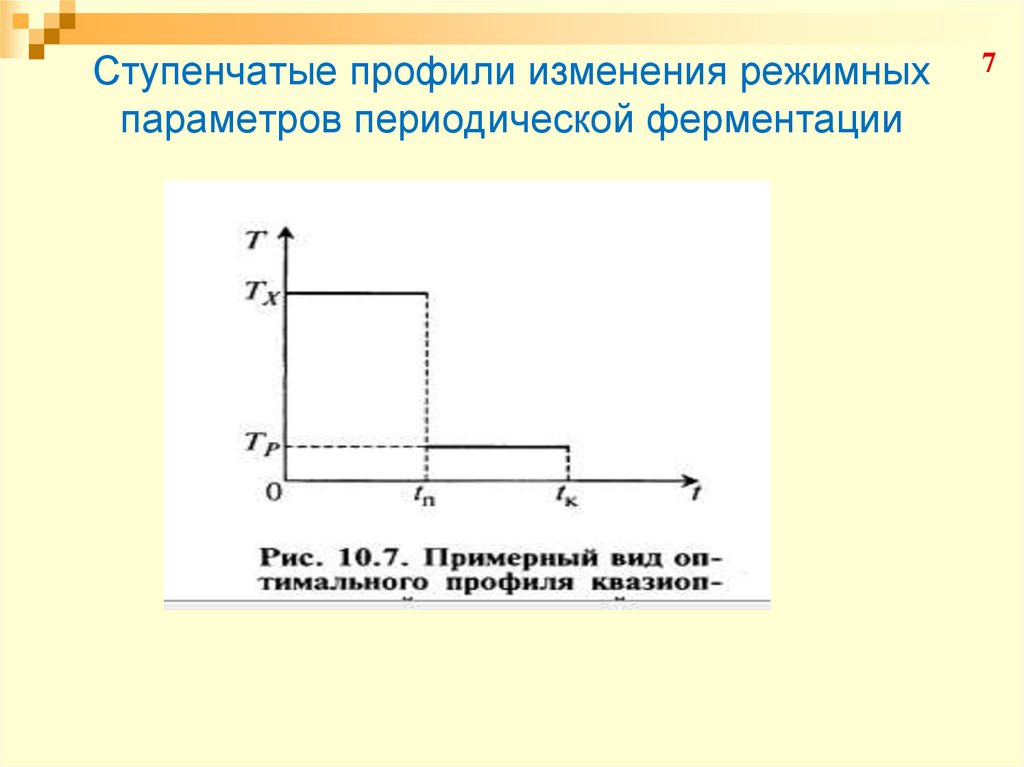
7. Ступенчатые профили изменения режимных параметров периодической ферментации

7

8. Ступенчатые профили изменения режимных параметров периодической ферментации

8

9. Ступенчатые профили изменения режимных параметров периодической ферментации

При (t = tк):
В первом периоде ферментации (при t > tп):
В точке переключения (при t = tп):
9

10. Ступенчатые профили изменения режимных параметров периодической ферментации

При (t > tк) рост биомассы подчиняется
выражению:
При t = tк :
10

11. Ступенчатые профили изменения режимных параметров периодической ферментации

Расчет квазиоптимальной программы управления:
11

12. Ступенчатые профили изменения режимных параметров периодической ферментации

Расчет квазиоптимальной программы управления:
12

13. Ступенчатые профили изменения режимных параметров периодической ферментации

Расчет квазиоптимальной программы управления:
13

14. Особенности регулирования концентрации субстрата в периодических и полупериодических процессах

14

15. Особенности регулирования концентрации субстрата в периодических и полупериодических процессах

15

16. Косвенные методы управления в процессах с подпиткой

Заранее рассчитывается программа u(t) изменения
подпитки во времени, и субстрат подается в аппарат без
информации о том, с какой скоростью его потребляется
культура (может привести как к избытку, так и недостатку
субстрата в среде);
Субстрат подается по одному из косвенных параметров,
связанных с ростом культуры. Это может быть величина
рН, концентрация растворенного кислорода,
интенсивность дыхания (подобно рН-стату, оксистату и
респиростату).
Процесс с подпиткой субстратом не может продолжаться сколь угодно
долго (объем жидкости возрастает). В этом случае переходят к
процессу с чередованием отбора части жидкости из аппарата с
продолжением подпитки между отборами (процесс ферментации с
повторяющимися попдитками «repeatead fed-batch»)
16

17. Оптимизация времени завершения периодической ферментации

Средняя продуктивность процесса:
17

18. Оптимизация времени завершения периодической ферментации

Способы, при которых можно улучшить ход процесса
ферментации:
изыскание более продуктивного штамма-продуцента;
поддержание в ходе процесса ферментации оптимальной
концентрации субстрата;
поддержание в ходе процесса ферментации оптимальных
значений температуры и величины рН (не обязательно на
постоянном уровне, а меняя их по определенной программе);
поддержание в ходе процесса оптимального режима по
параметрам аэрации – концентрации в среде растворенного
кислорода и растворенного углекислого газа;
поддержание оптимального режима перемешивания
ферментационной жидкости в аппарате.
18

19. Преимущества и недостатки периодических и полупериодических процессов ферментации

Преимущества:
малая стоимость аппарата и системы управления;
гибкость – возможность наработки в одном реакторе разных
продуктов;
процесс менее подвержен инфицированию и мутациям клеток
из-за отсутствия протока и притока и из-за относительно
малого времени процесса ферментации;
процесс удобен для получения малых количеств продукта;
условия культивирования можно поддерживать в оптимуме
как в фазе роста биомассы, так и в фазе биосинтеза
продукта (оптимальные условия биомассы и продукта могут
быть различны);
процесс удобен для реализации биосинтеза вторичных
метаболитов.
19

20. Преимущества и недостатки периодических и полупериодических процессов ферментации

Недостатки:
необходимость приготовления посевного материала;
велико непродуктивное время ферментации;
в связи с необходимостью частой стерилизации быстрее
изнашиваются измерительные приборы, особенно датчики
величины рН);
производительность по биомассе и продукту часто ниже, чем
в непрерывном процессе;
труднее поддерживать необходимые параметры из-за
нестационарности периодического процесса;
процесс более опасен для персонала ( аппарат чаще
открывают, моют, что сопряжено с контактом человека с
м/о и продуктами их жизнедеятельности.
20

21. Кинетика процессов ферментации

21
Кинетика процессов ферментации
Кинетика процессов ферментации изучает закономерности
изменения скорости роста м/о и биосинтеза продуктов
метаболизма в зависимости от текущих концентраций субстратов,
биомассы, продуктов метаболизма, температуры и рН

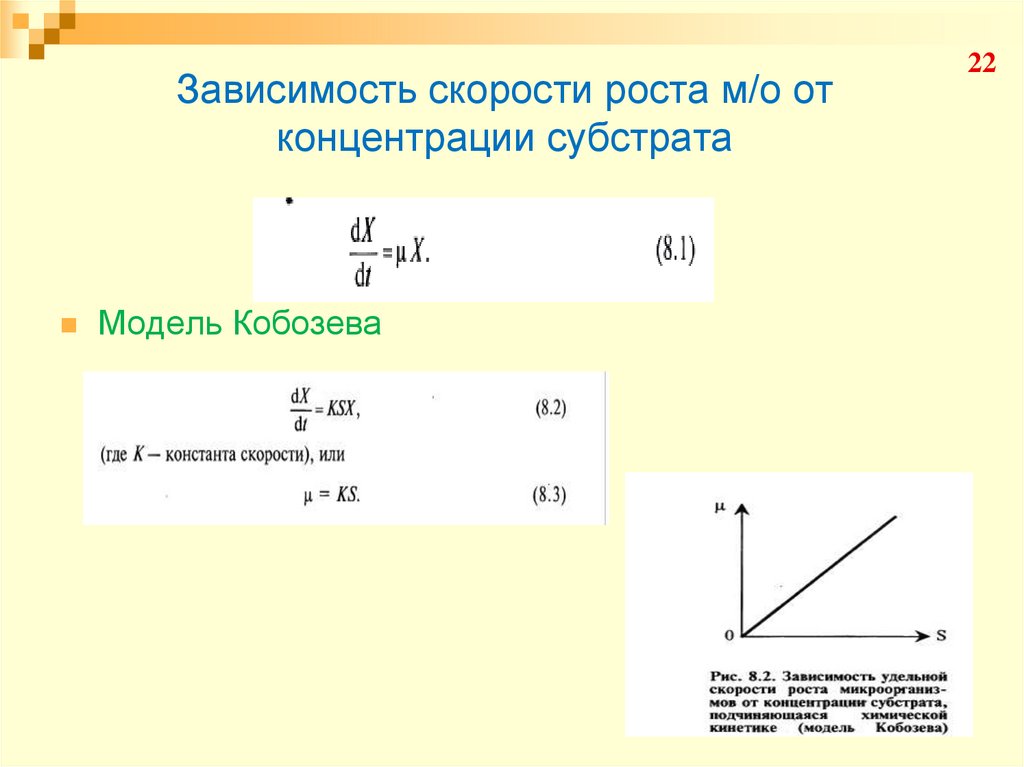
22. Зависимость скорости роста м/о от концентрации субстрата

Модель Кобозева
22

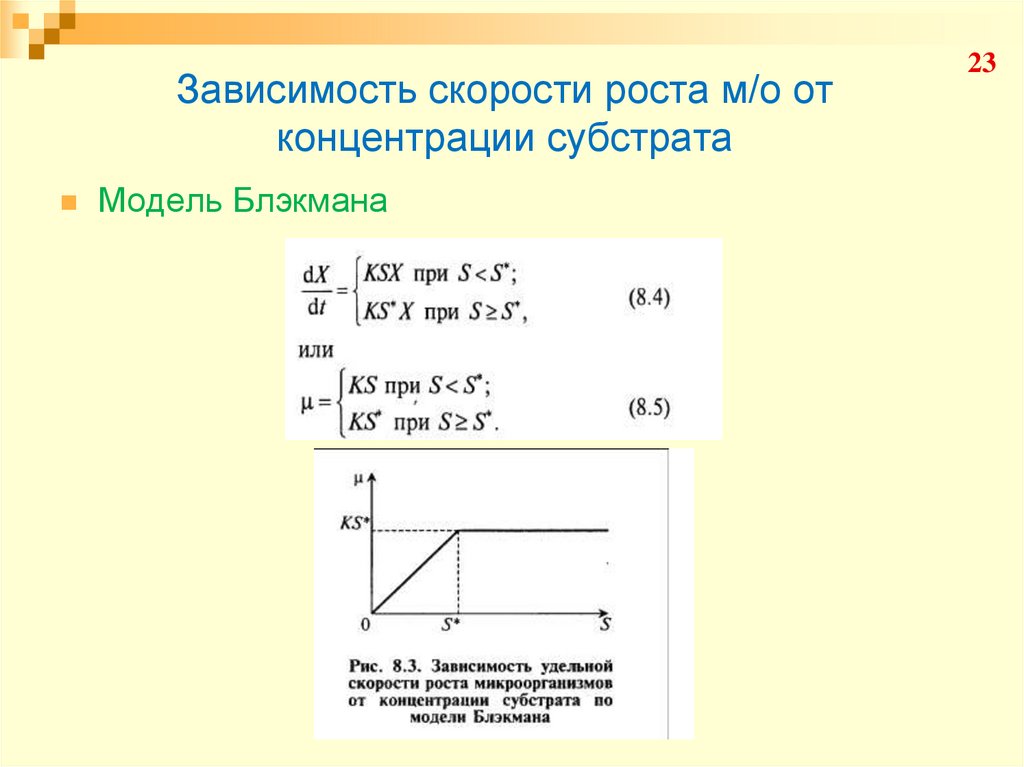
23. Зависимость скорости роста м/о от концентрации субстрата

Модель Блэкмана
23

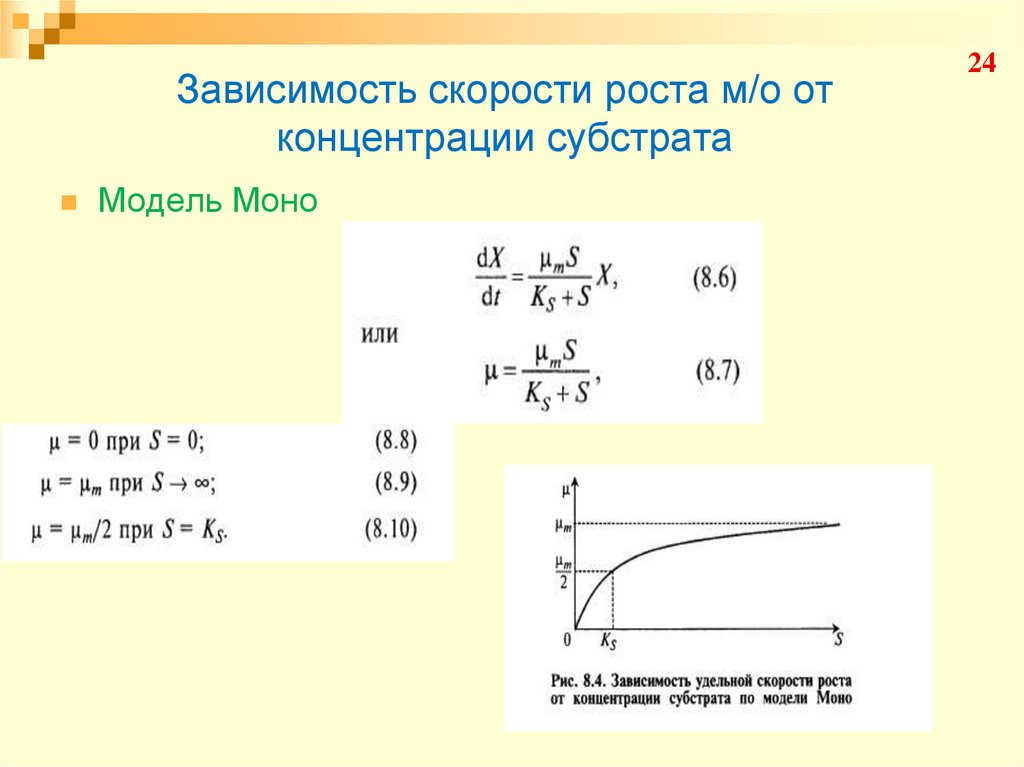
24. Зависимость скорости роста м/о от концентрации субстрата

Модель Моно
24

25. Зависимость скорости роста м/о от концентрации субстрата

Модель Моно
25

26. Зависимость скорости роста м/о от концентрации субстрата

Модель Моно
26

27. Зависимость скорости роста м/о от концентрации субстрата

Модель Мозера
27

28. Зависимость скорости роста м/о от концентрации субстрата

Модель Перта:
28

29. Зависимость скорости роста м/о от концентрации субстрата

Модель Андрюса:
29

30. Зависимость скорости роста м/о от концентрации субстрата

Модель Андрюса:
30

31. Зависимость скорости роста м/о от концентрации субстрата

Модель Андрюса:
31

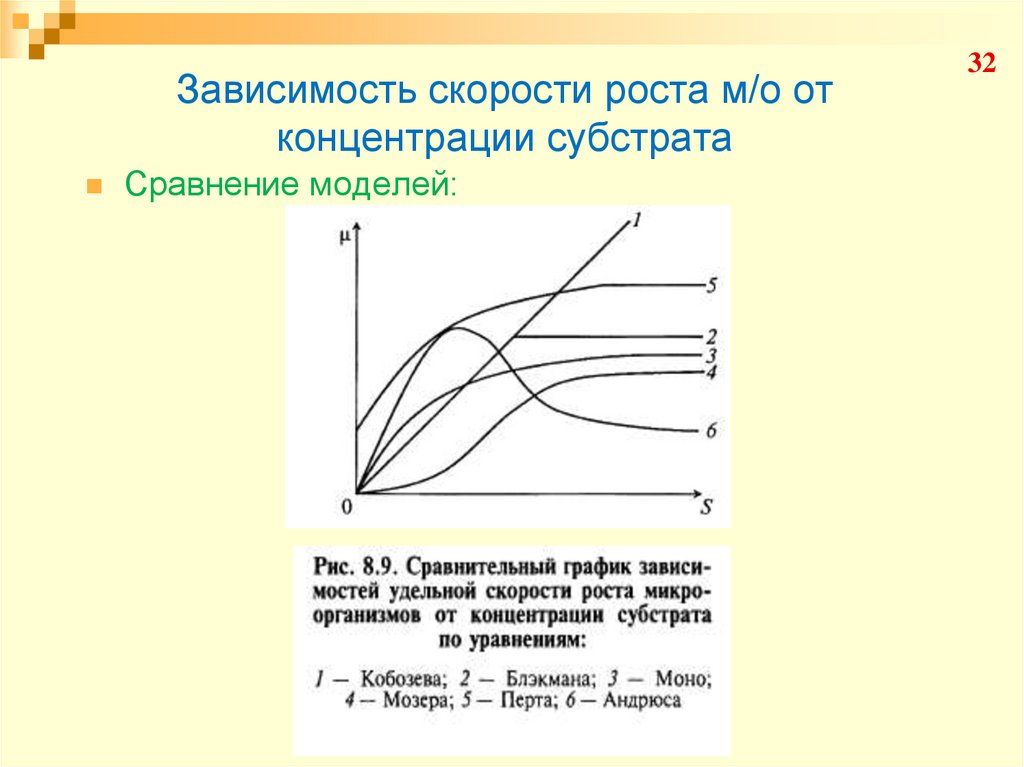
32. Зависимость скорости роста м/о от концентрации субстрата

Сравнение моделей:
32

33. Зависимость скорости роста м/о от концентрации продукта метаболизма

Модель Хишельвуда:
33

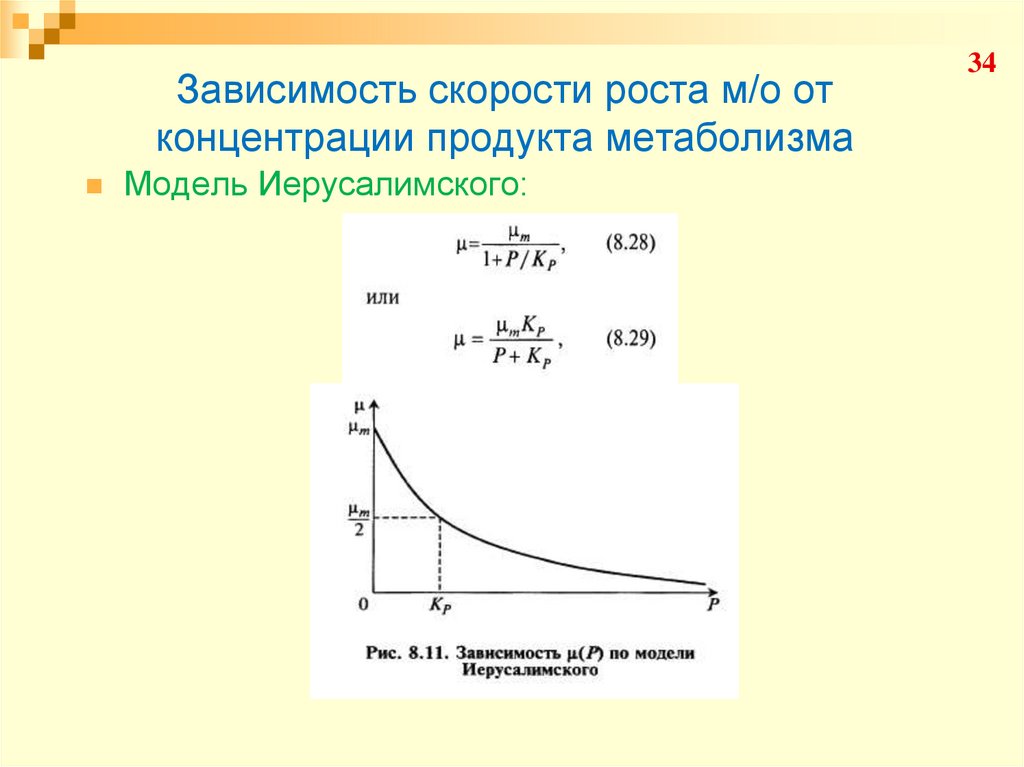
34. Зависимость скорости роста м/о от концентрации продукта метаболизма

Модель Иерусалимского:
34

35. Зависимость скорости роста м/о от концентрации продукта метаболизма

Модель Иерусалимского:
35

36. Зависимость скорости роста м/о от концентрации продукта метаболизма

Модель Иерусалимского:
36

37. Зависимость скорости роста м/о от концентрации продукта метаболизма

Модель Бергтера:
37

38. Зависимость скорости роста м/о от концентрации продукта метаболизма

Частично ингибирующий продукт:
38

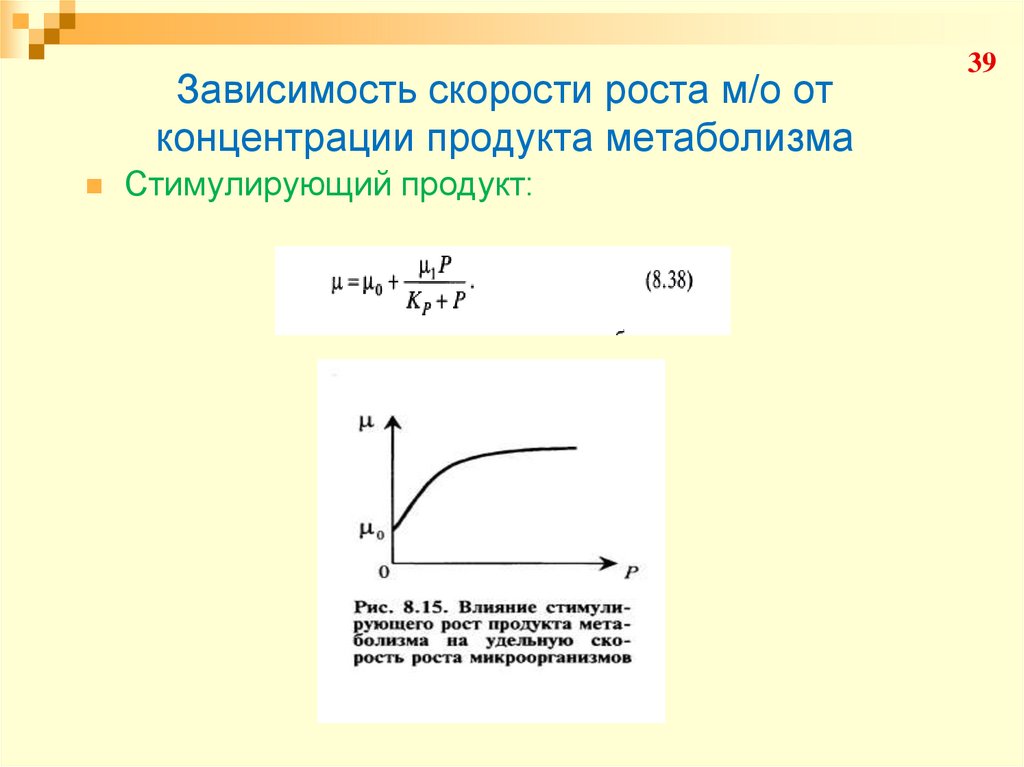
39. Зависимость скорости роста м/о от концентрации продукта метаболизма

Стимулирующий продукт:
39

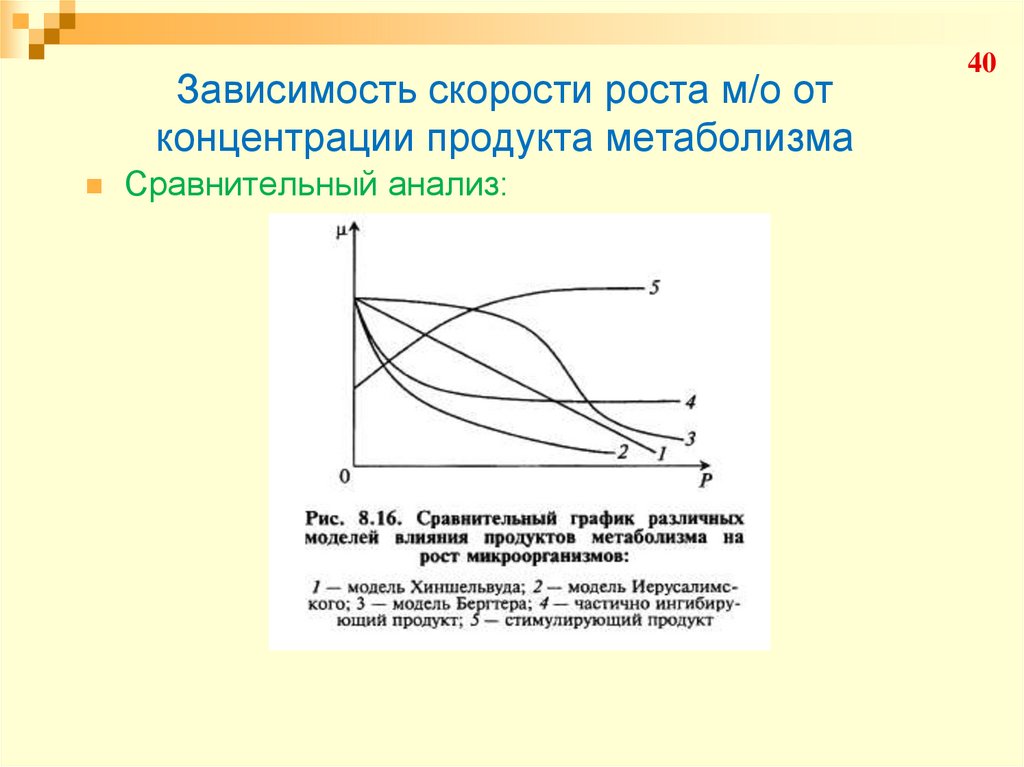
40. Зависимость скорости роста м/о от концентрации продукта метаболизма

Сравнительный анализ:
40

41. Многофакторные кинетические уравнения

1.
«Многосубстратные» уравнения:
Мультипликативные уравнения – функция является
произведением многофакторных зависимостей
Каждый фактор автономен и может иметь свою
собственную зависимость (один субстрат по Моно, а
второй – с ингибированием по Андрюсу):
41

42. Многофакторные кинетические уравнения

«Многосубстратные» уравнения:
2. Аддитивные уравнения – многофакторная функция
является суммой однофакторных:
3. Альтернативные уравнения – многофакторная
зависимость подчиняется принципу кинетического
минимума:
Уравнение показывает, что для каждого субстрата
существует зависимость μ(Si), когда лимитирующим
фактором является только этот субстрат
42

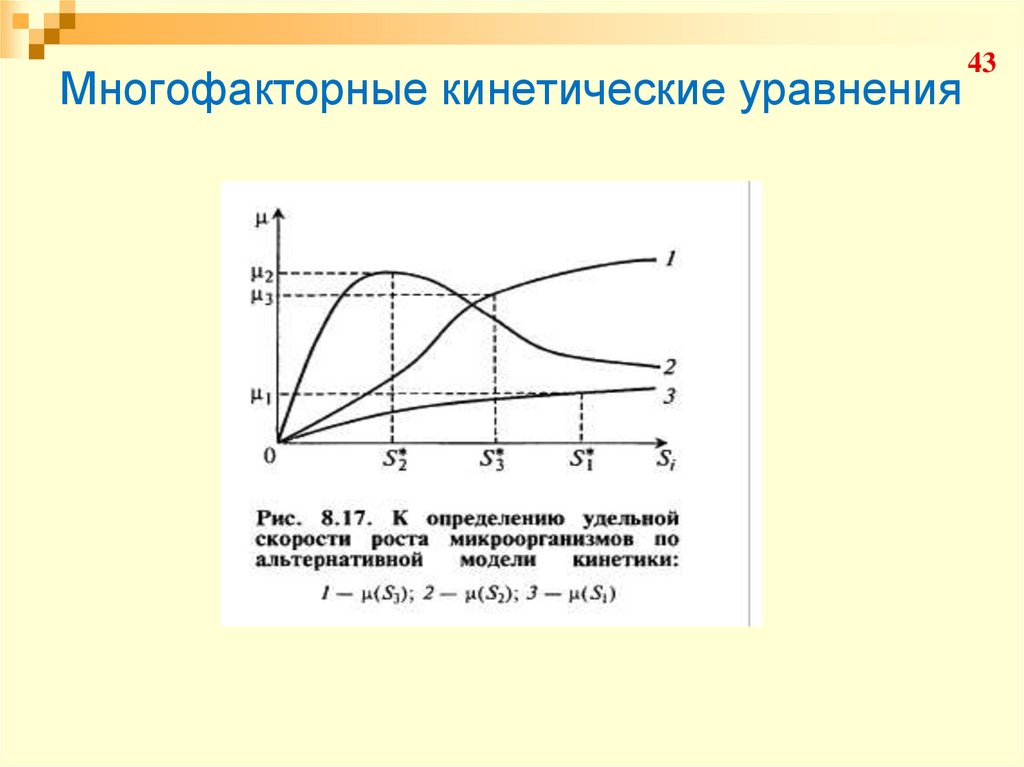
43. Многофакторные кинетические уравнения

43

44. Многофакторные кинетические уравнения

«Многосубстратные» уравнения:
4. Уравнения с неразделяющими переменными.
Существует уравнение конкурентного торможения
вторым субстратом:
44

45. Многофакторные кинетические уравнения

1.
Многофакторные уравнения со смешанными
факторами:
Моно-Иерусалимского:
2. Конкурентного торможения продуктом метаболизма:
3 . Контуа – учитывающее влияние концентрации
биомассы на вид зависимости удельной скорости роста
от концентрации субстрата:
45

46. Многофакторные кинетические уравнения

46

47. Многофакторные кинетические уравнения

47
Многофакторные уравнения со смешанными
факторами:
Если в ур-е Моно-Иерусалимского подставить комплекс
Николаева (S0 – S) вместо Р, то получается вместо
двухфакторного однофакторное кинетическое
уравнение:

48. Отмирание (диссимиляция) биомассы

Рост-диссимиляция
Отсутствие отмирания:
Уравнение Герберта (удельная скорость отмирания биомассы
является величиной постоянной):
Уравнение Ферхюльста( удельная скорость роста принята
пропорциональной концентрации биомассы, а общая скорость
отмирания пропорциональна квадрату концентрации биомассы)
48

49. Отмирание (диссимиляция) биомассы

49
Уравнение Рамкришны (удельная скорость диссимиляции биомассы
пропорциональна концентрации ингибирующих продуктов
метаболизма:
Уравнение Колпакова (связывает удельную скорость диссимиляции с
концентрацией субстрата):

50. Кинетика деградации (инактивации) продуктов метаболизма

Не всегда синтезированные продукты метаболизма отличаются
устойчивостью (часто они лабильны и разрушаются уже в процессе
самой ферментации), поэтому описывая материальный баланс по
продукту метаболизма, необходимо учитывать кинетику его
инактивации:
Варианты моделирования:
Деградация отсутствует:
Деградация идет с постоянной скоростью:
Реакция разложения первого порядка:
Реакция разложения по уравнению химической кинетики:
50

51. Кинетика деградации (инактивации) продуктов метаболизма

Варианты моделирования:
Реакция разложения зависит не только от концентрации продукта,
но и от концентрации биомассы:
Скорость реакции разложения зависит от концентрации биомассы и
возрастает с концентрацией продукта до какого-то предела::
51

52. Кинетика потребления субстрата

Чтобы «замкнуть» материальный баланс, в котором почти во всех
уравнениях участвует концентрация субстрата, необходимо
дополнить его уравнением кинетики потребления:
52

53. Кинетика потребления субстрата

Для каждого интервала времени Δt можно определить ΔX, ΔP и Х
(берут среднее значение для интервала). Подставив найденные
числовые значения, получаем линейное уравнение с тремя
неизвестными:
Для одного интервала для определения всех трех коэффициентов
недостаточно. Нужны минимум 3 точки, которые дадут три
уравнения (можно найти 3 коэффициента). Лучше взять больше
точек, чем число искомых коэффициентов, тогда получается
система уравнений, в которой коэффициенты находят методом
наименьших квадратов
53

54. Расчет коэффициентов выхода и скоростей роста и биосинтеза продукта по данным периодической ферментации

54

55. Расчет коэффициентов выхода и скоростей роста и биосинтеза продукта по данным периодической ферментации

55

56. Расчет коэффициентов выхода и скоростей роста и биосинтеза продукта по данным периодической ферментации

56

57. Графический метод расчет коэффициентов Yхs и m о экспериментальным данным

57

58. Потоки в центральном метаболизме Saccharomyces cerevisiae

58
Процесс оценки потоков сводится к поиску
наиболее подходящей модели, которая описывает
метаболизм. Для изучения метаболических потоков
в центральном метаболизме углерода модельной
системой S. Cerevisiae (клетки выращивают в
хемостате в аэробных условиях в режиме «stadystate» с удельной скоростью роста 0,1 ч-1 и в
«batch» культуре с удельной скоростью роста 0,37
ч-1. (глюкоза лимитирующий субстрат).

59.

59

60. Потоки в центральном метаболизме Saccharomyces cerevisiae

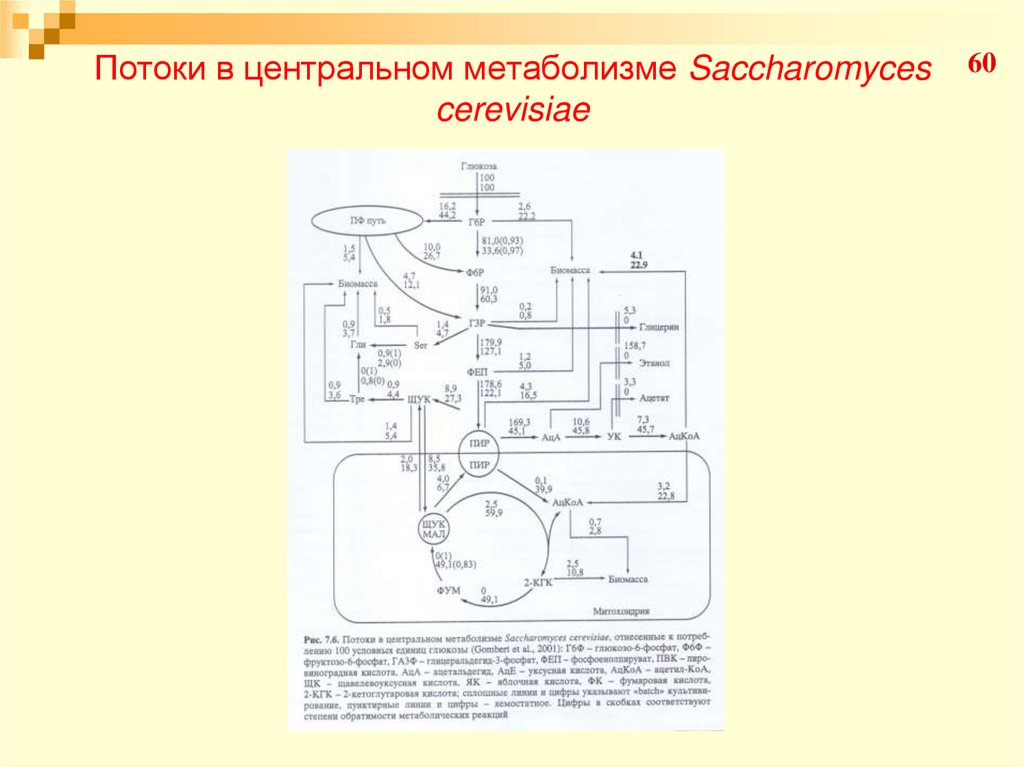
60

61. Потоки в центральном метаболизме Saccharomyces cerevisiae

61
В «batch» культуре16,2 молекул глюкозы из
каждых 100 расходуется по пентозофосфатному
пути, в хемостате – 44,2 молекул глюкозы на 100.
В противоположность культуре, растущей в
хемостате, ЦТК не функционировал как цикл в
«batch» культуре

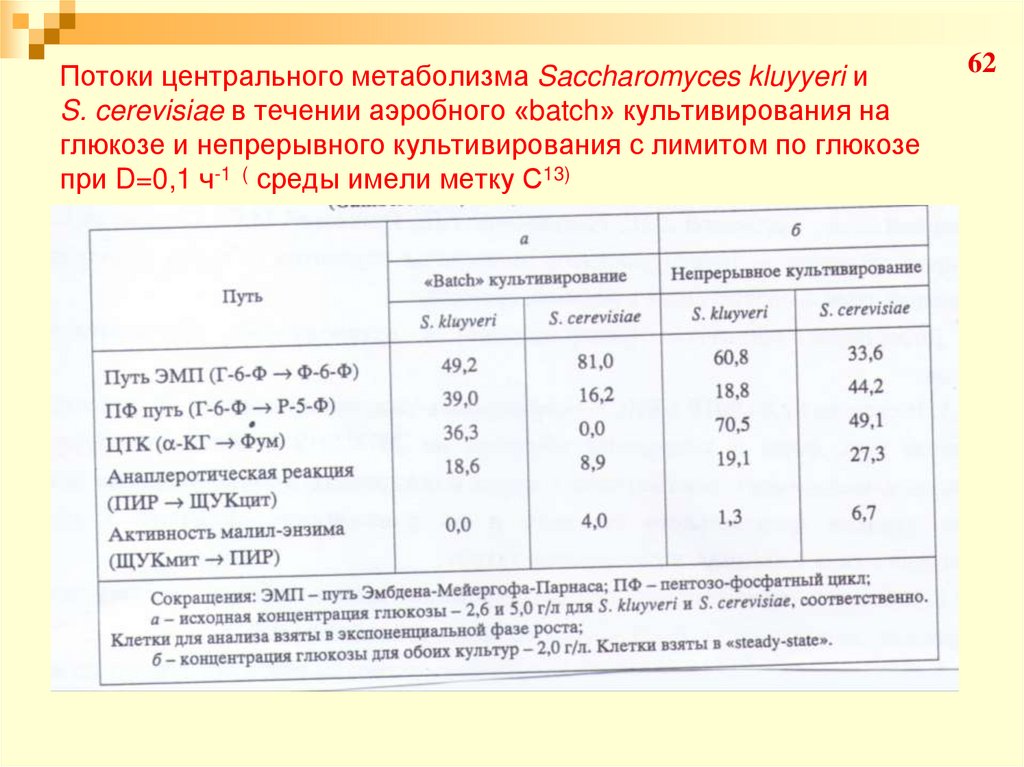
62. Потоки центрального метаболизма Saccharomyces kluyyeri и S. cerevisiae в течении аэробного «batch» культивирования на глюкозе и

непрерывного культивирования с лимитом по глюкозе
при D=0,1 ч-1 ( среды имели метку С13)
62

63. Потоки центрального метаболизма Saccharomyces kluyyeri и S. cerevisiae

63
Для S. Kluyyeri:
Потоки ЭМП : ПФ : биомасса распределились в соотношении 49
: 39 : 12 («batch») и 61 : 19 : 20 (непр.)
Увеличение потока ЭМП и потока в биомассе, падал поток в
направлении ПФ в непрерывной культуре по сравнению с «batch»
Для S. Cerevisiae:
ЭМП : ПФ : биомасса – 81 : 16 : 3 («batch») и 34 : 44 : 22 (непр.).
Увеличенную активность ПФ пути относительно потребления
глюкозы в непрерывной по сравнению с («batch»), объясняется
нарастающей потребностью в НАДФН для синтеза биомассы.
Наблюдаемое различие в потоках, расходящихся от глюкозо-6фосфата, как точки ответвления при «batch» сахаромицетов,
объясняет различие в выходе биомассы (0,39 и 0,11г/г глюкозы )

64. Потоки центрального метаболизма Saccharomyces kluyyeri и S.сerevisiae

64
Анализ потоков на уровне ЦТК необходимы для оценки этапов
метаболизма.
При («batch») культивировании S.сerevisiae поток от α-кетоглутаровой
кислоты до фумаровой практически отсутствует (ЦТК функционирует
как две ветви), а у S.kluyyeri он составлял 36 ммоль/100 ммоль
использованной глюкозы ( в («batch» условиях ЦТК функционирует как
цикл).
При непрерывном культивировании поток от α-кетоглутаровой кислоты
до фумаровой был определен величиной в 70,5 ммоль/100 ммоль
глюкозы у S.kluyyeri и 49 ммоль/100 ммоль глюкозы у S.сerevisiae .
Для оптимизации процесса получения лимонной кислоты была создана
модель идиофазы

65.

65