Similar presentations:
Построение и преобразование графиков тригонометрических функций
1.
Тригонометрическиефункции
Свойства.
Преобразование
графиков.
2.
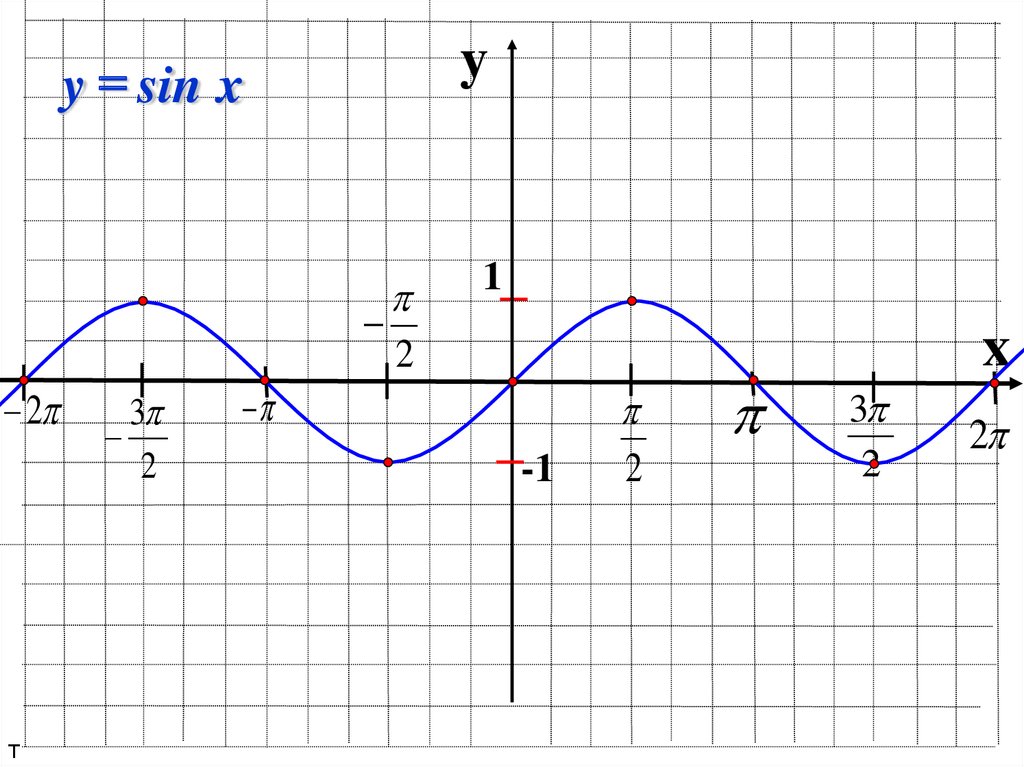
Функция y=sinx3.
yy = sin x
2
2
т
3
2
1
-1
2
x
3
2
2
4.
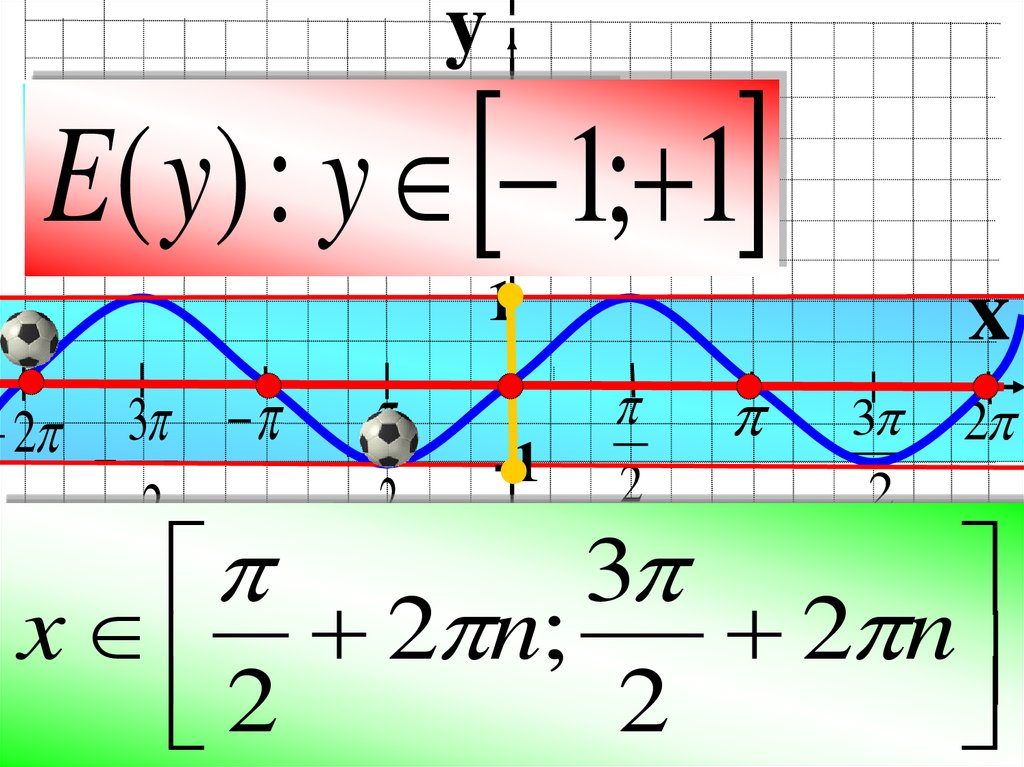
yED((yy))::yx R1; 1
x
1
2 3
2
2
-1
2
3
2
2
3
=2n ;n;n, n
xy = 0 x 2
2 nZ
22
22
5.
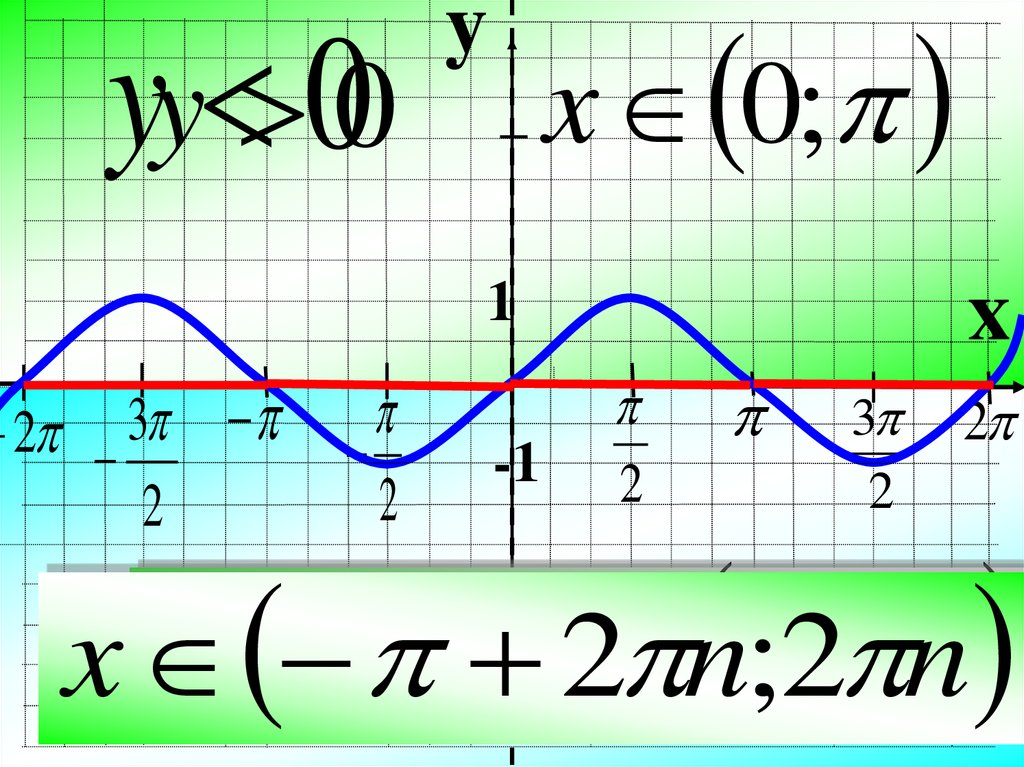
yy 00x 0;
y
x
1
2 3
2
2
-1
2
3
2
2
x
2 nx;2 n ;2 ;n0
x
6.
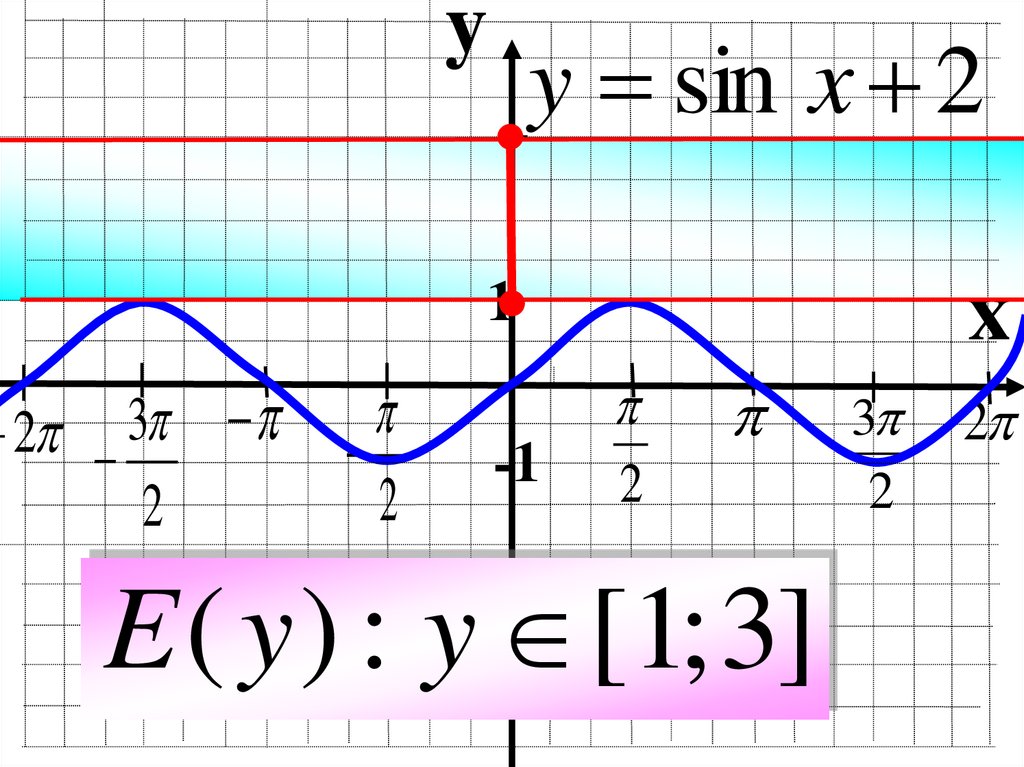
yy = sin x 2
x
1
2 3
2
2
-1
2
E ( y ) : y [1; 3]
3
2
2
7.
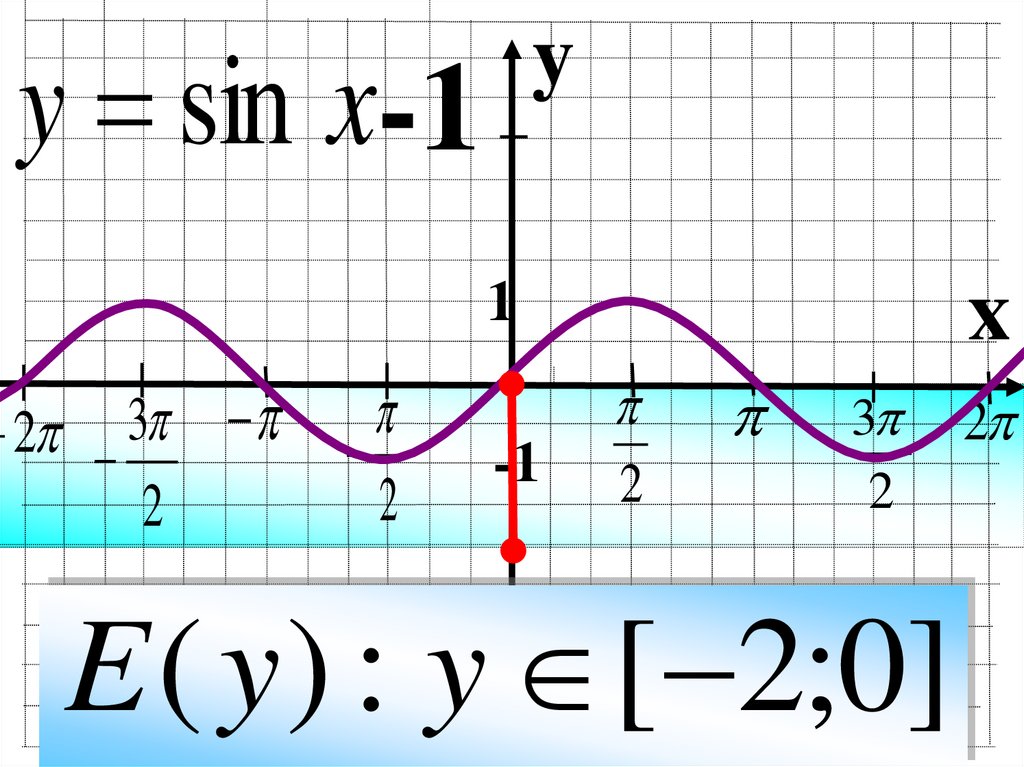
y = sin x-1y
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [ 2;0]
2
8.
y2
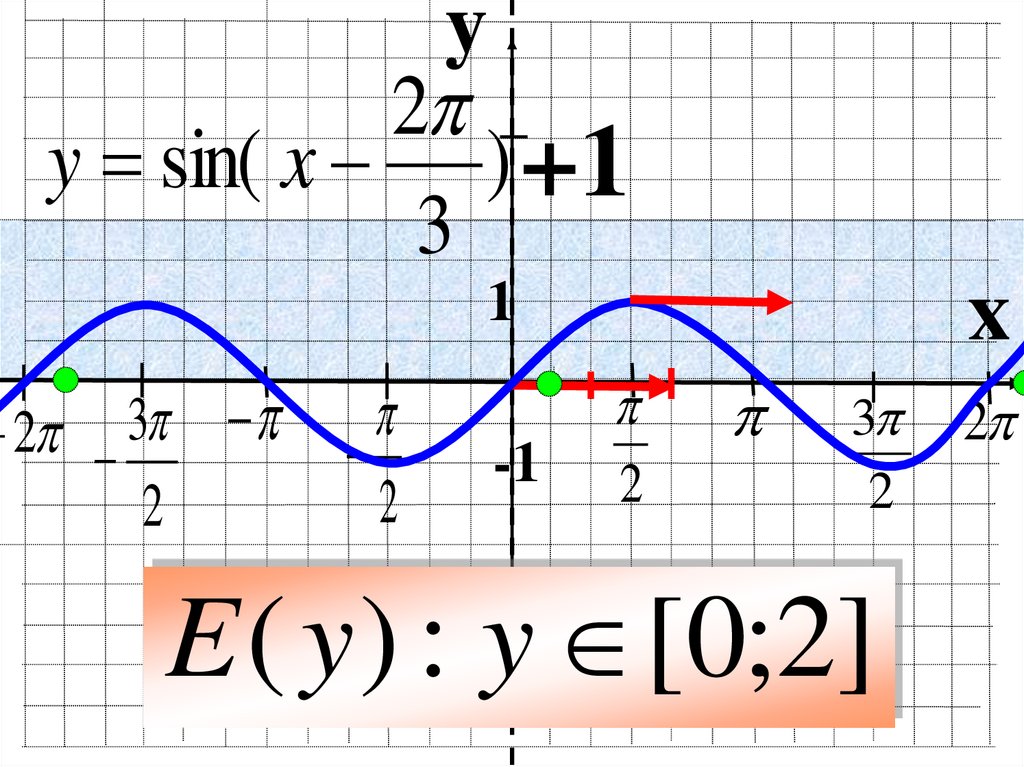
y = sin( x ) +1
3
x
1
2 3
2
2
-1
2
3
2
E ( y ) : y [0;2]
2
9.
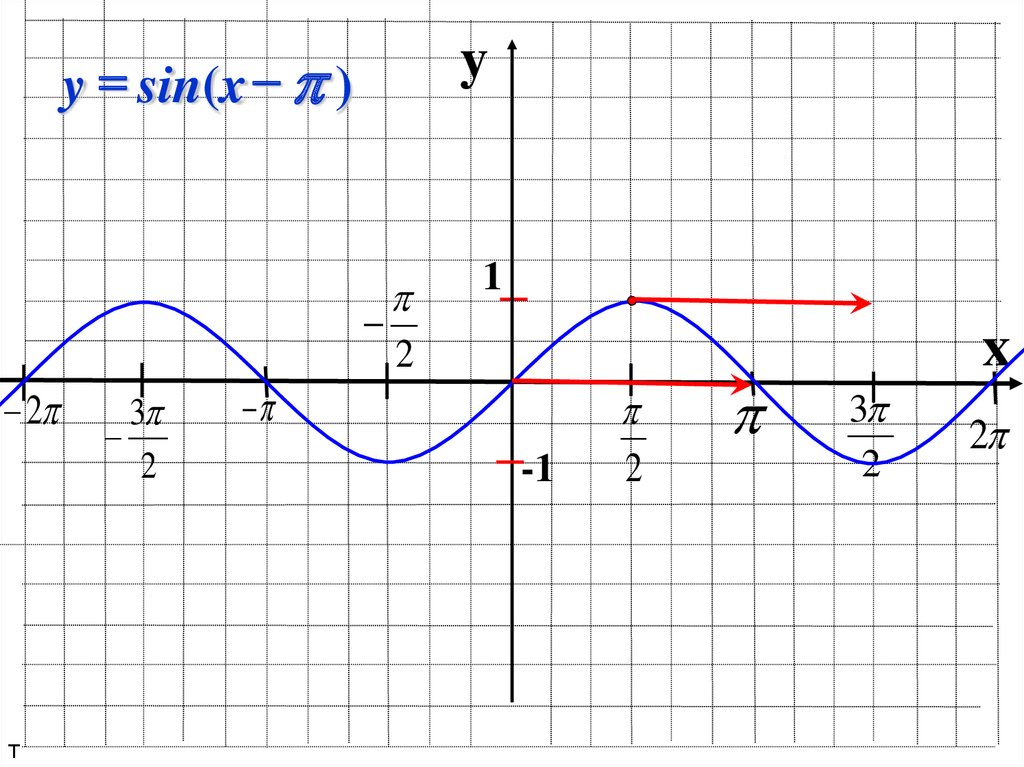
y = sin(x )y
2
2
т
3
2
1
-1
2
x
3
2
2
10.
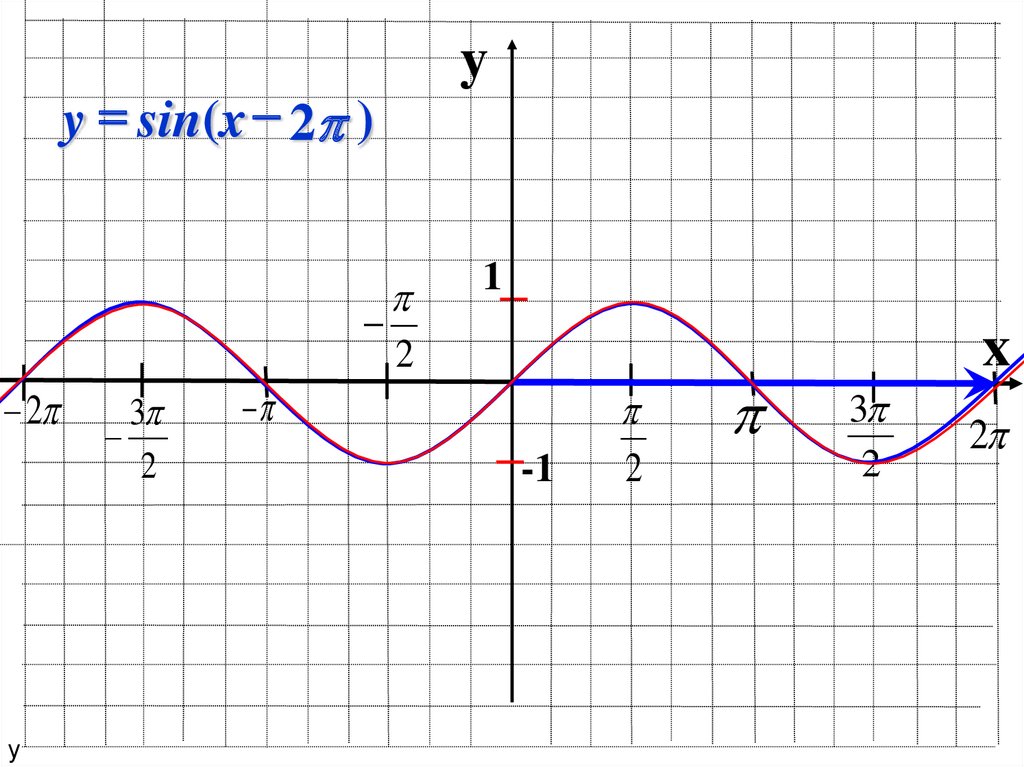
y = sin(x 2 )2
2
у
3
2
y
1
-1
2
x
3
2
2
11.
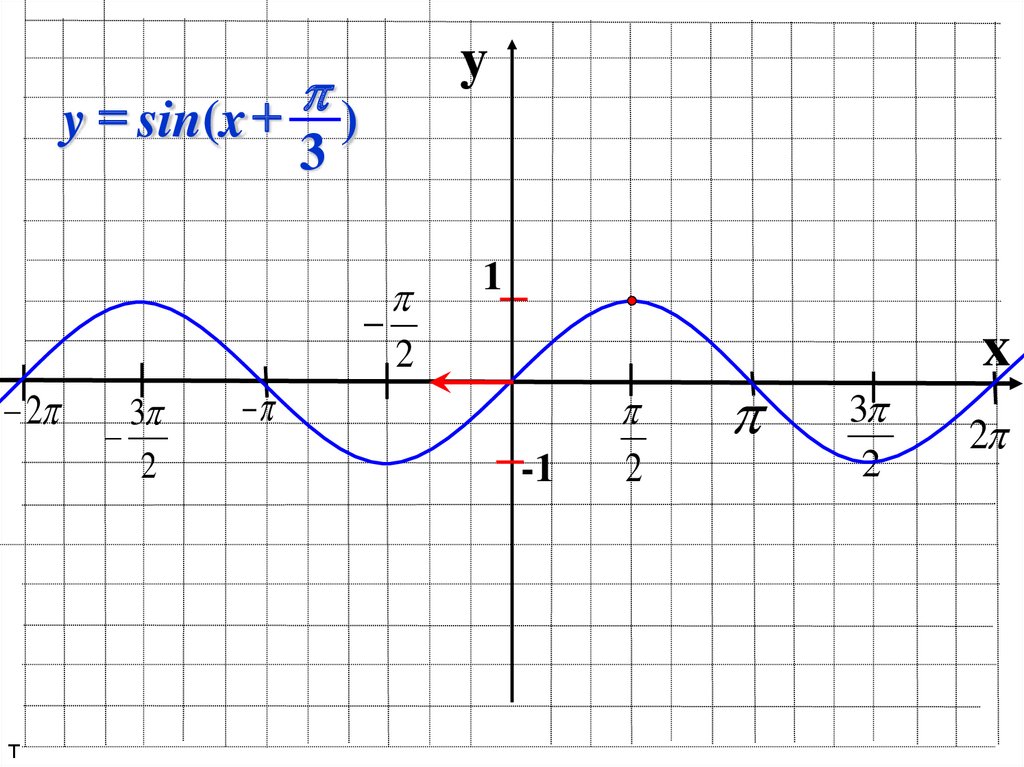
yy = sin(x )
3
2
2
т
3
2
1
-1
2
x
3
2
2
12.
13.
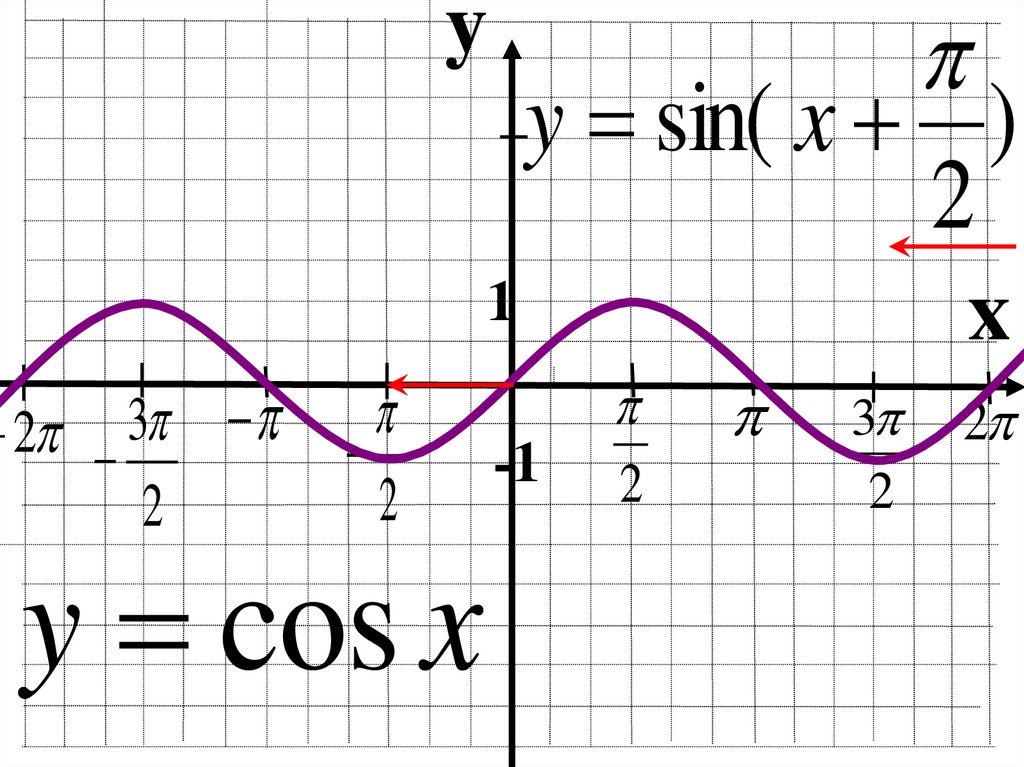
y = sin( x )2
y
x
1
2 3
2
2
y = cos x
-1
2
3
2
2
14.
y = cos x2
3
2
y
2
1
-1
2
x
3
2
2
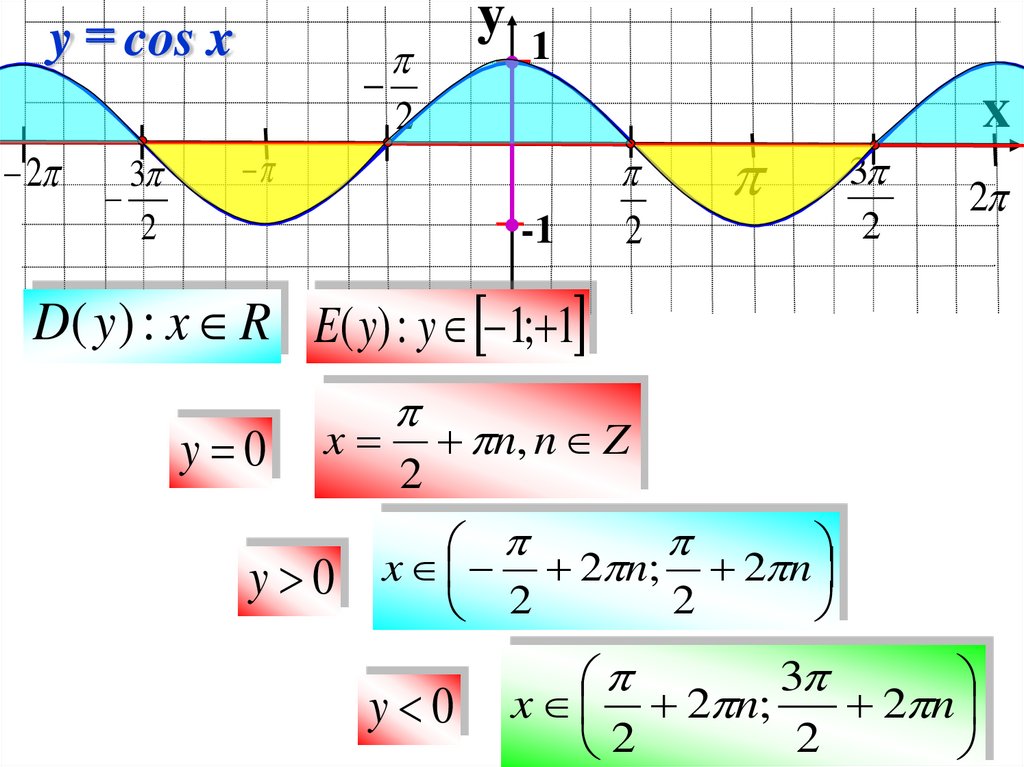
D( y ) : x R E( y) : y 1; 1
y=0
x=
y 0
2
n, n Z
x 2 n; 2 n
2
2
y 0
3
x 2 n;
2 n
2
2
15.
y = cos x2
3
2
2
y
1
-1
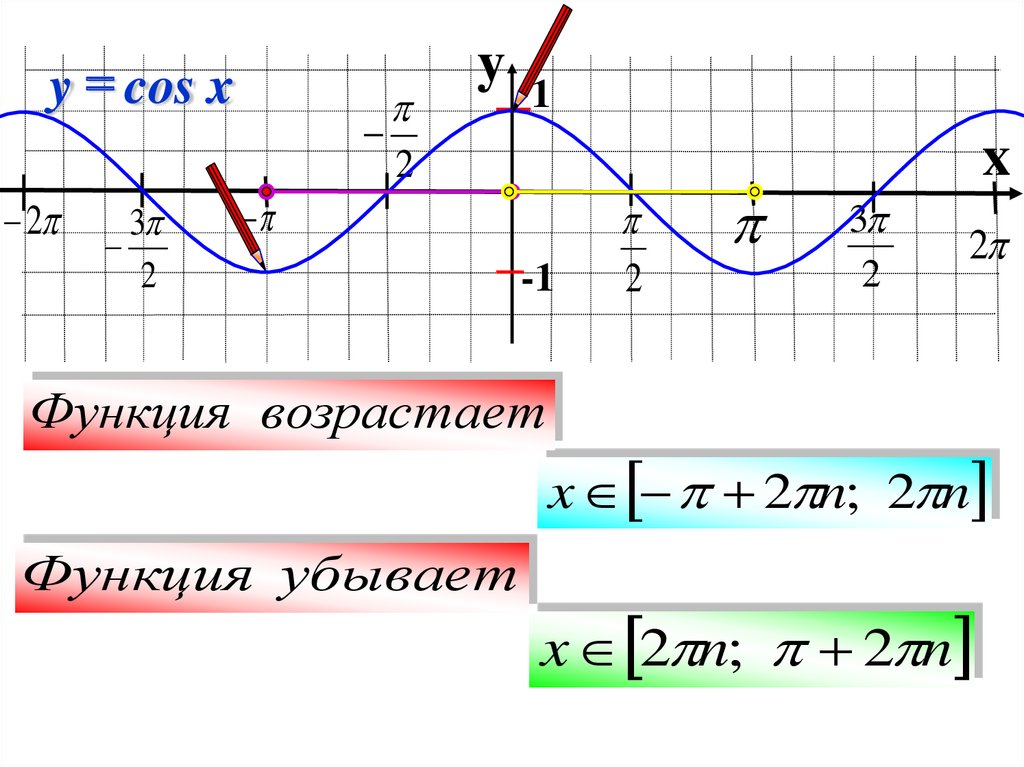
Функция возрастает
Функция убывает
2
x
3
2
2
x 2 n; 2 n
x 2 n; 2 n
16.
yy = cos x
2
3
2
2
1
-1
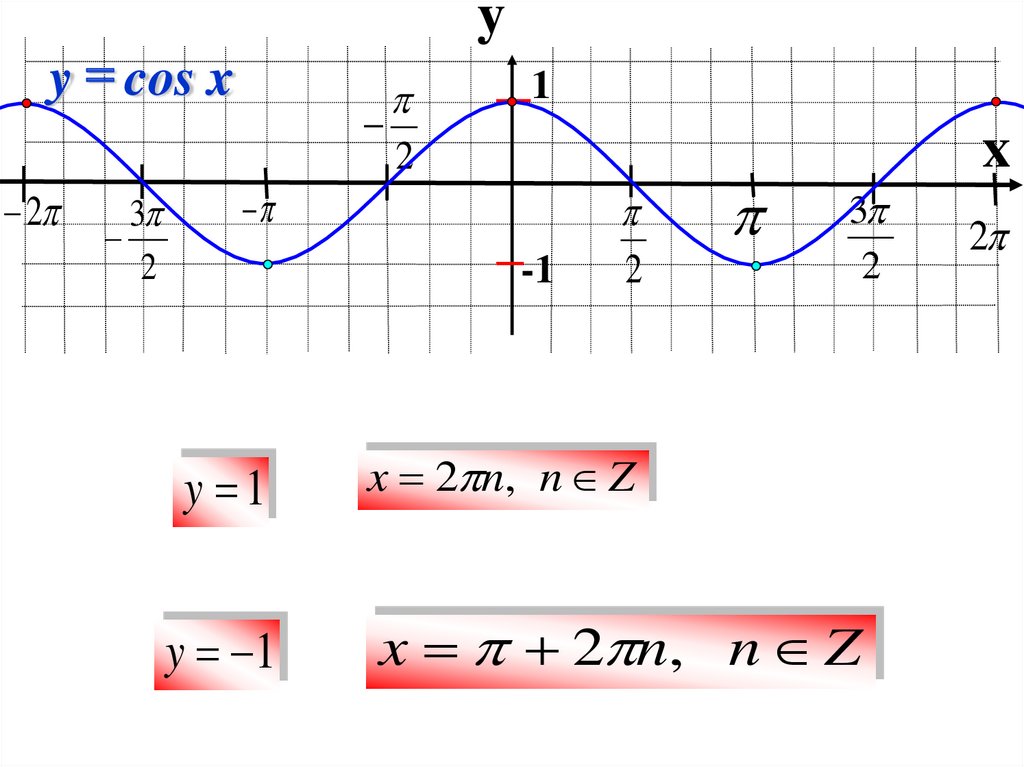
y =1
y = 1
2
x
3
2
x = 2 n, n Z
x = 2 n, n Z
2
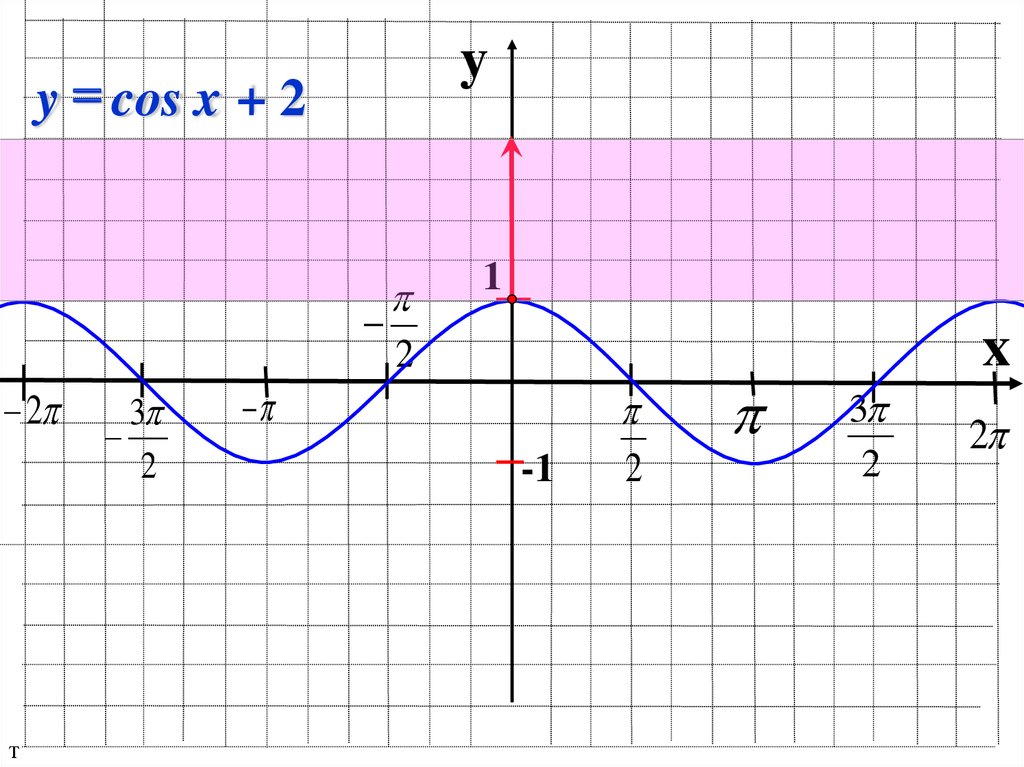
17.
yy = cos x + 2
2
2
т
3
2
1
-1
2
x
3
2
2
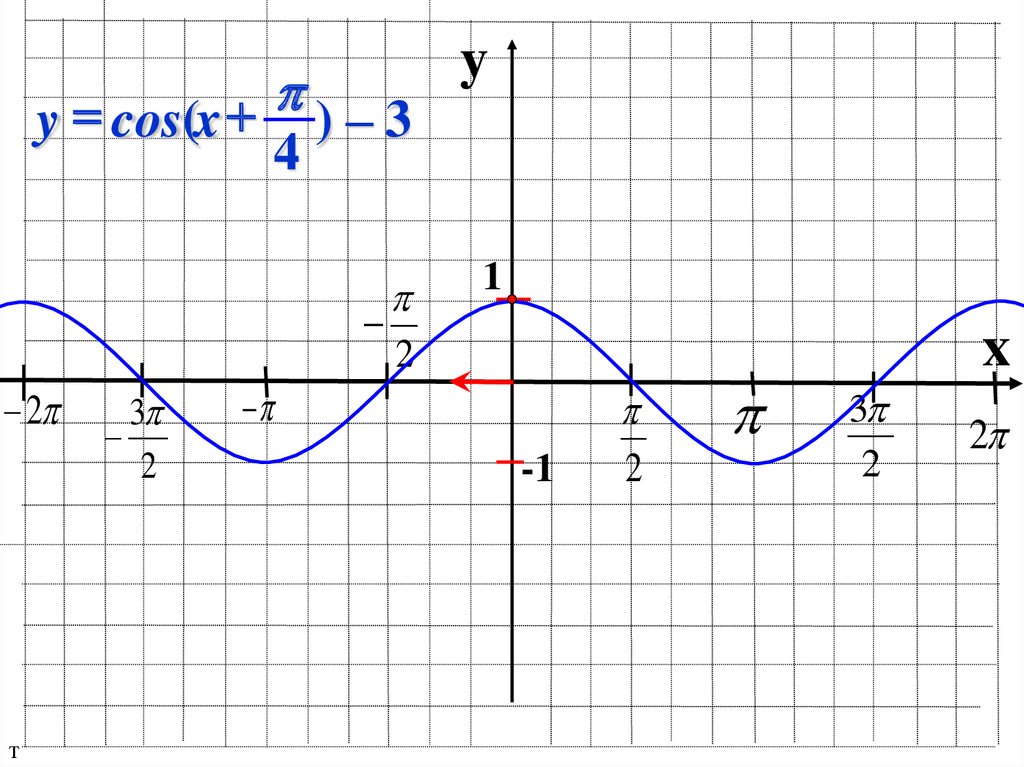
18.
y = cos(x ) – 3y
4
2
2
т
3
2
1
-1
2
x
3
2
2
19. Функция y=tg x
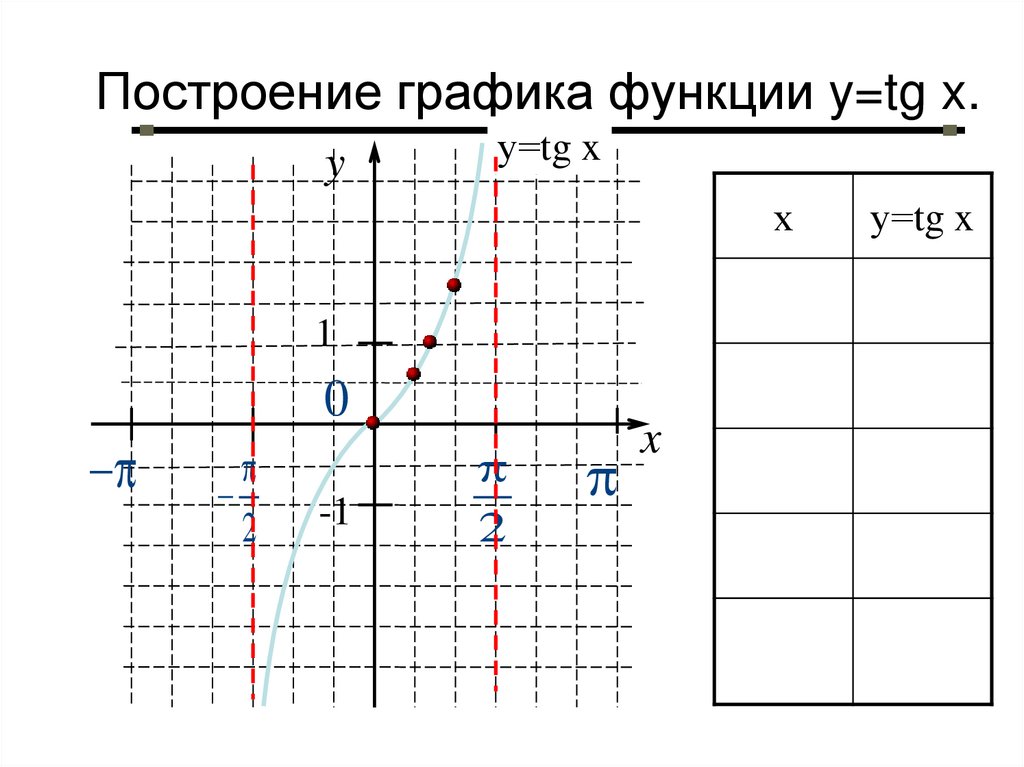
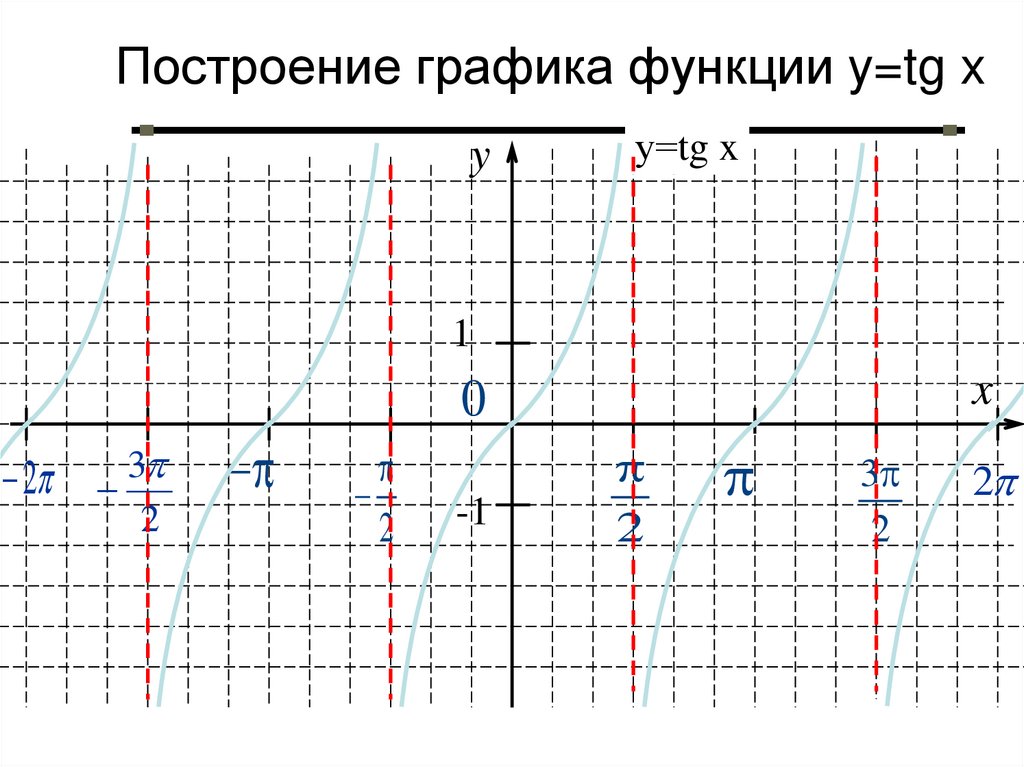
20. Построение графика функции y=tg x.
yу=tg x
1
0
2
-1
2
x
х
у=tg x
0
0
π ∕6
1∕ 3
π ∕4
1
π ∕3
3
π ∕2
Не
сущ.
21. Построение графика функции y=tg x
yу=tg x
1
x
0
2
3
2
2
-1
2
3
2
2
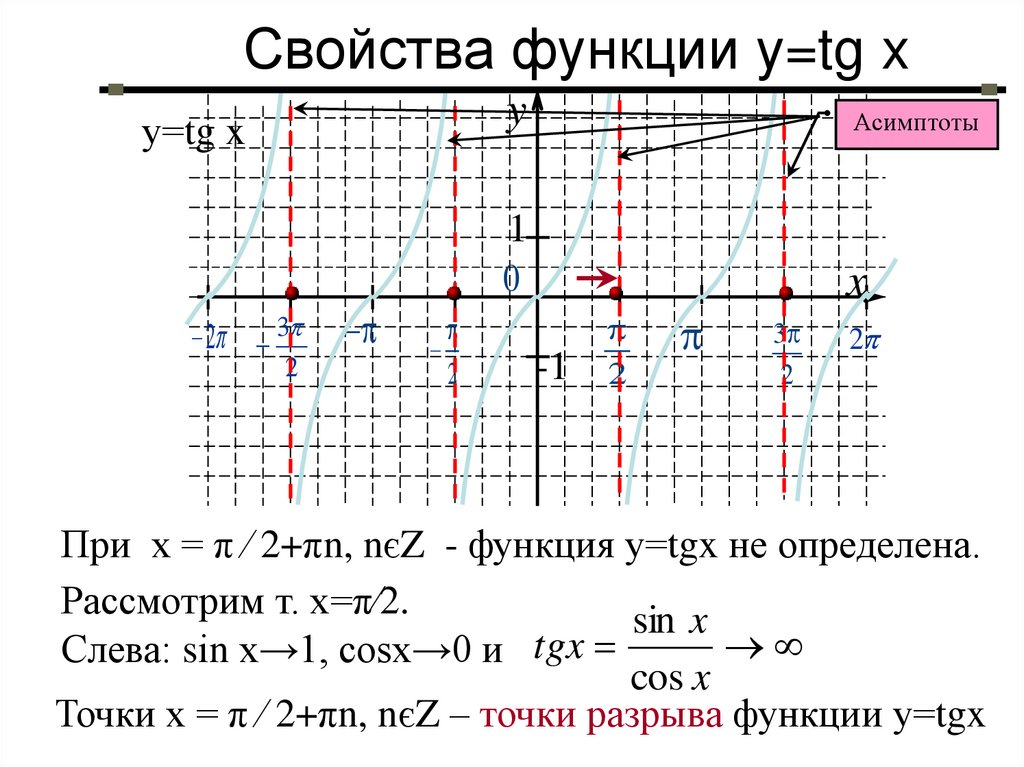
22. Свойства функции y=tg x
у=tg x2
3
2
2
y
Асимптоты
1
0
x
-1
2
3
2
2
При х = π ∕ 2+πn, nєZ - функция у=tgx не определена.
Рассмотрим т. х=π∕2.
sin x
Слева: sіn x→1, сosx→0 и tgx =
cos x
Точки х = π ∕ 2+πn, nєZ – точки разрыва функции у=tgx
23. Свойства функции y=tg x
1. Обл. определения: х n, n Z2
2. Множество значений функции: уєR
3. Периодическая, Т= π
4. Нечётная функция
5. Возрастает на всей области определения
6. Нули функции у (х) = 0 при х = πn, nєZ
7. у(х)>0 при хє (0; π/2) и при сдвиге на πn,nєZ
8. у(х)<0 при хє (-π/2; 0) и при сдвиге на πn, nєZ
9. При х = π ∕ 2+πn, nєZ - функция у=tgx не
определена Имеет точки разрыва графика и
асимптоты
24. Функция y=ctg x.
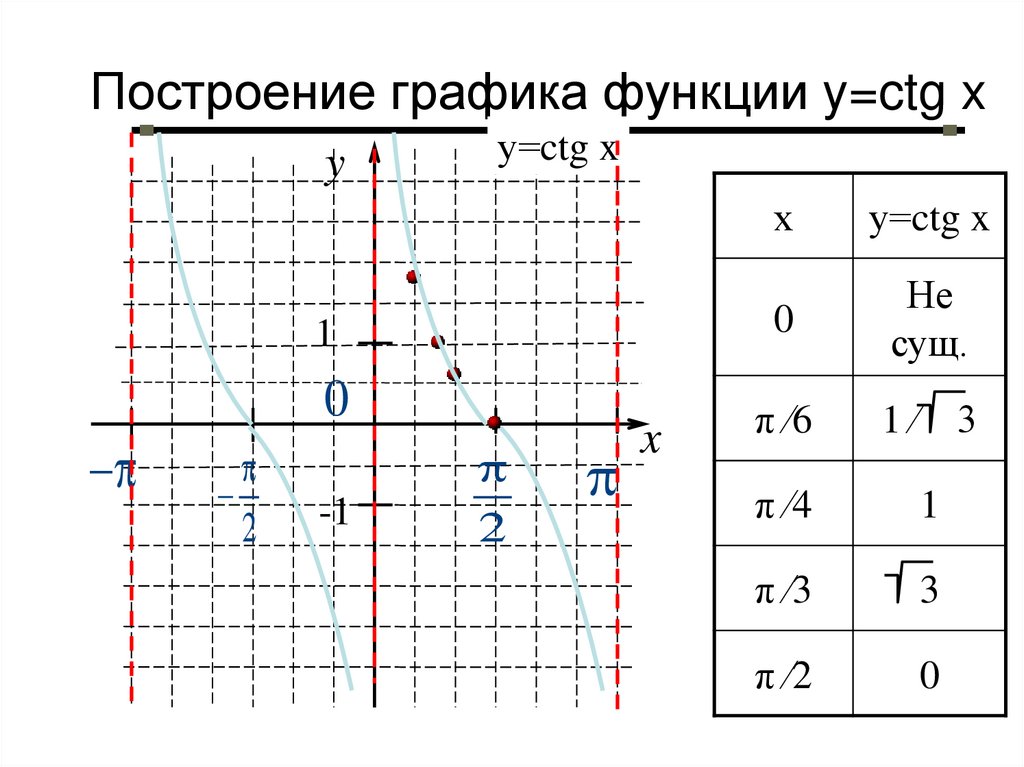
25. Построение графика функции y=ctg x
yу=ctg x
1
0
2
-1
2
x
х
у=ctg x
0
Не
сущ.
π ∕6
1∕
3
π ∕4
1
π ∕3
3
π ∕2
0
26.
Опишите свойства функции y = ctgx.1) D(f): множество всех действительных чисел, кроме чисел
вида x = k.
2) Периодическая с периодом .
3) Нечётная функция.
4) Функция убывает на любом интервале вида ( k; + k).
5) Функция не ограничена ни снизу, ни сверху.
6) Функция не имеет ни наибольшего, ни наименьшего
значений.
7) Функция непрерывна на любом интервале вида ( k; + k).
8) E(f) = (- ; + ).
27. Примеры построение графиков
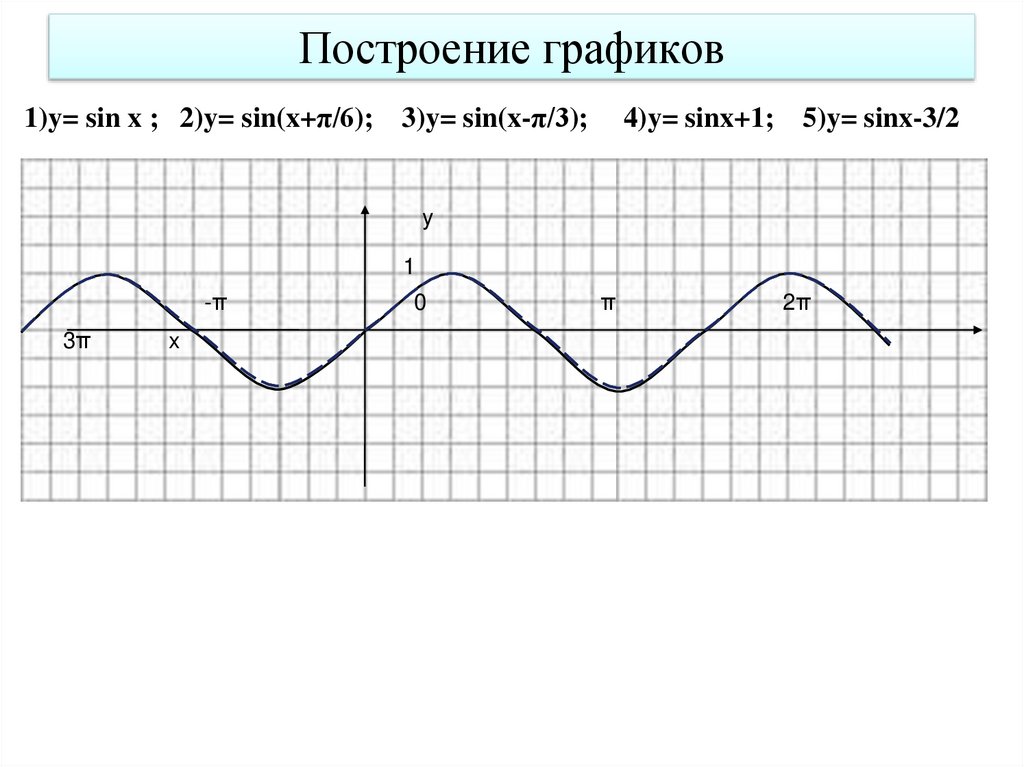
28. Построение графиков
1)y= sin x ; 2)y= sin(x+π/6); 3)y= sin(x-π/3);4)y= sinx+1; 5)y= sinx-3/2
y
1
-π
3π
x
0
π
2π
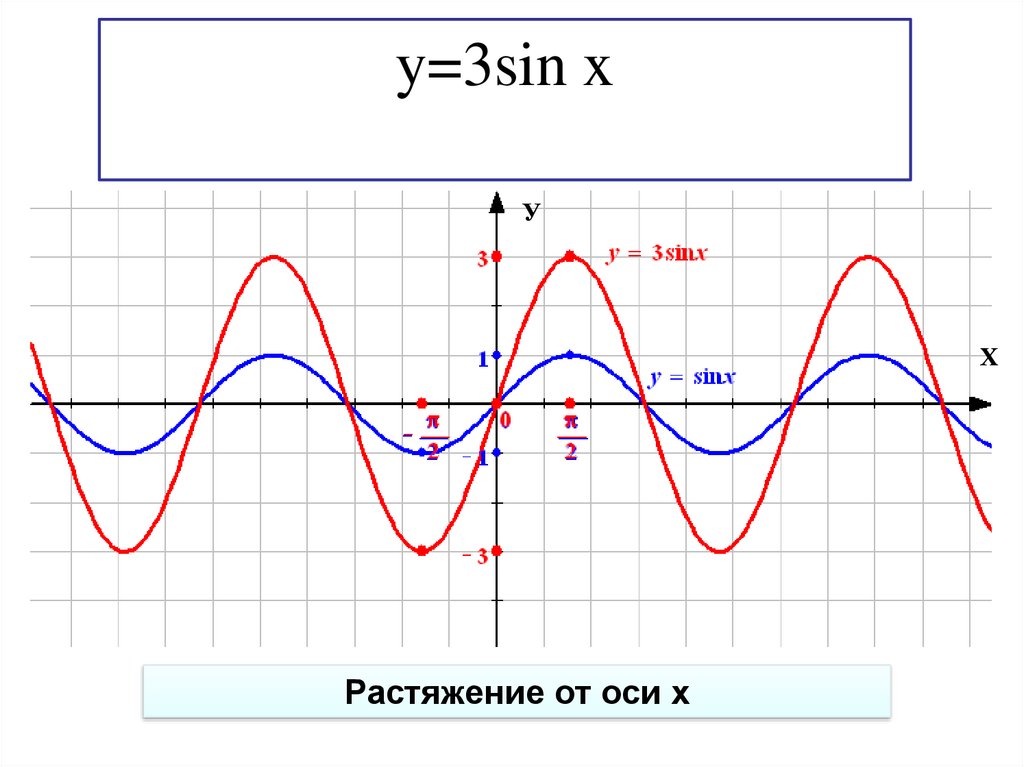
29.
y=3sin xУ
Х
Растяжение от оси х
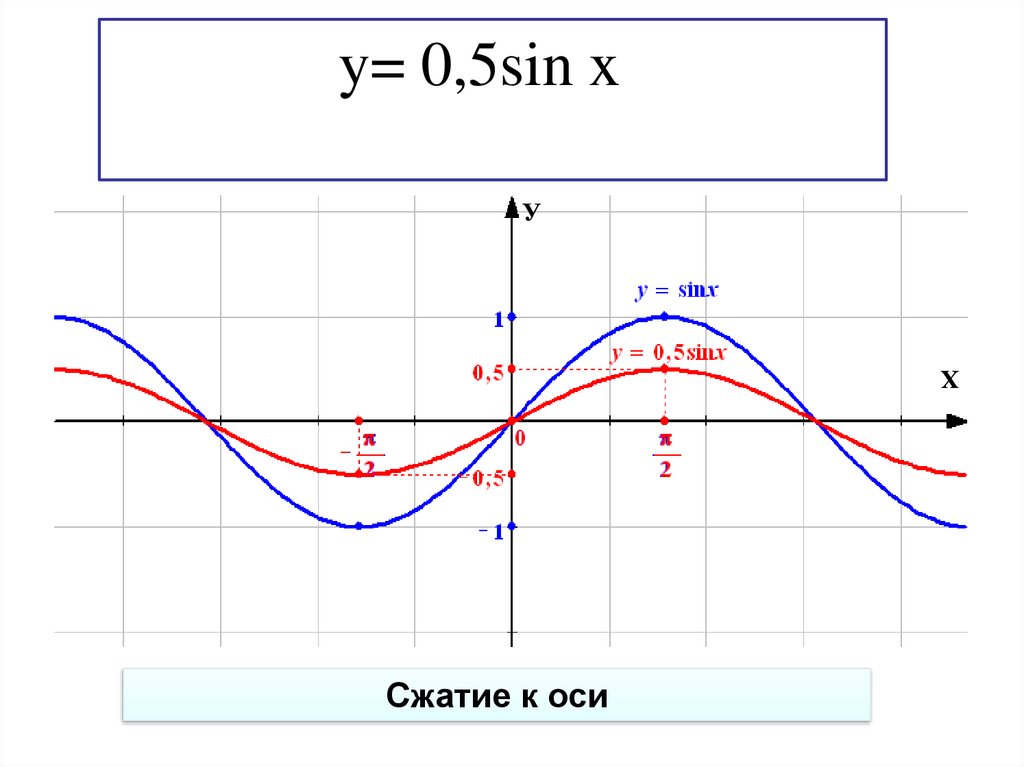
30.
y= 0,5sin xУ
Х
Сжатие к оси
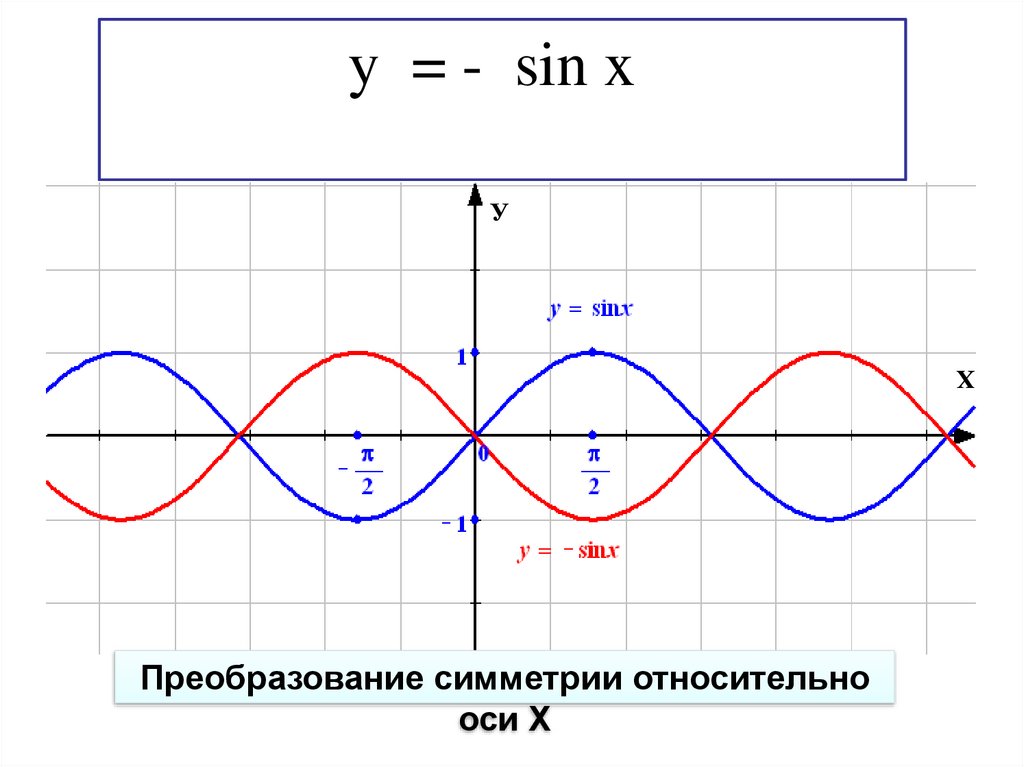
31.
y = - sin xУ
Х
Преобразование симметрии относительно
оси Х
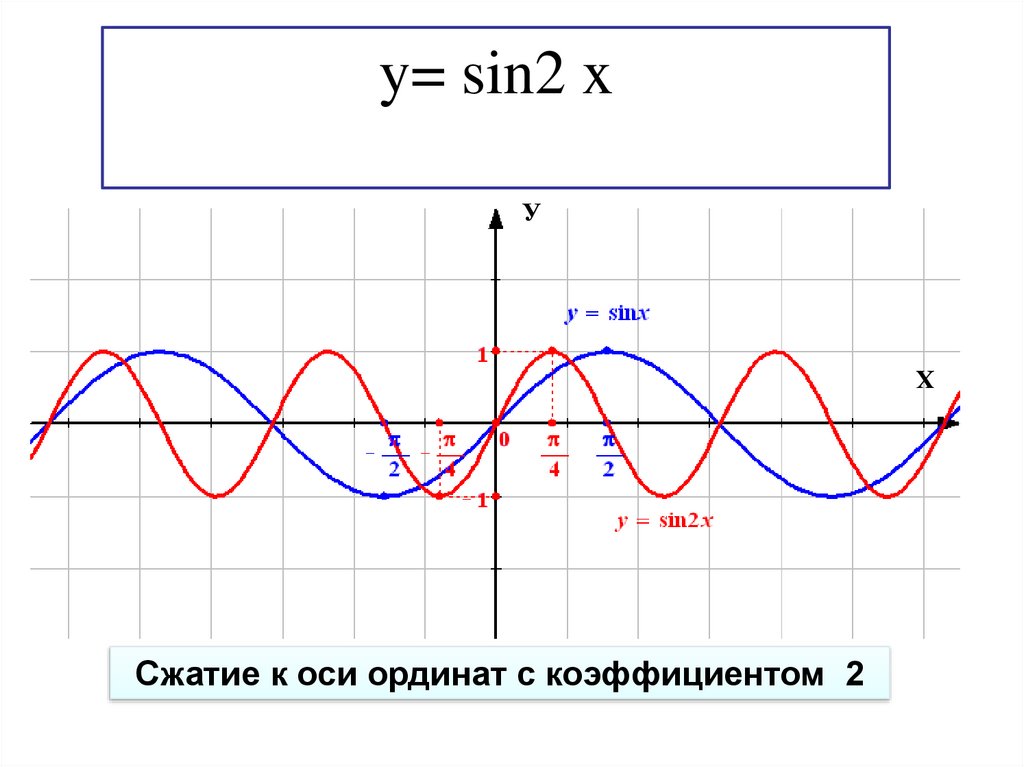
32.
y= sin2 xУ
Х
Сжатие к оси ординат с коэффициентом 2
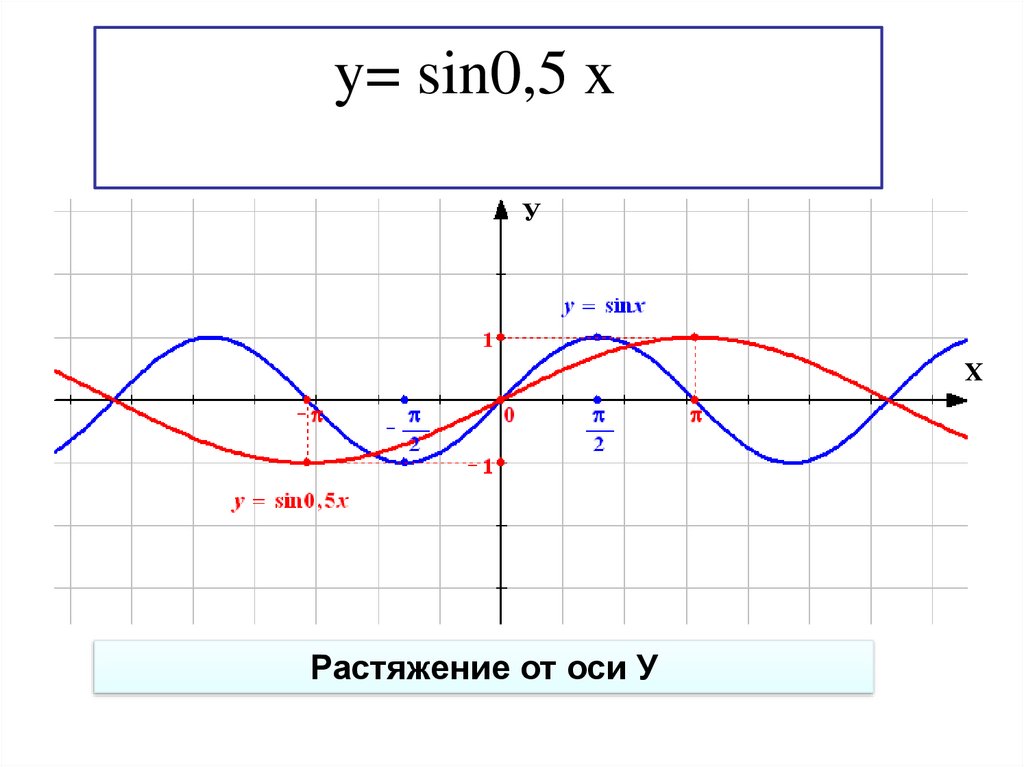
33.
y= sin0,5 xУ
Х
Растяжение от оси У
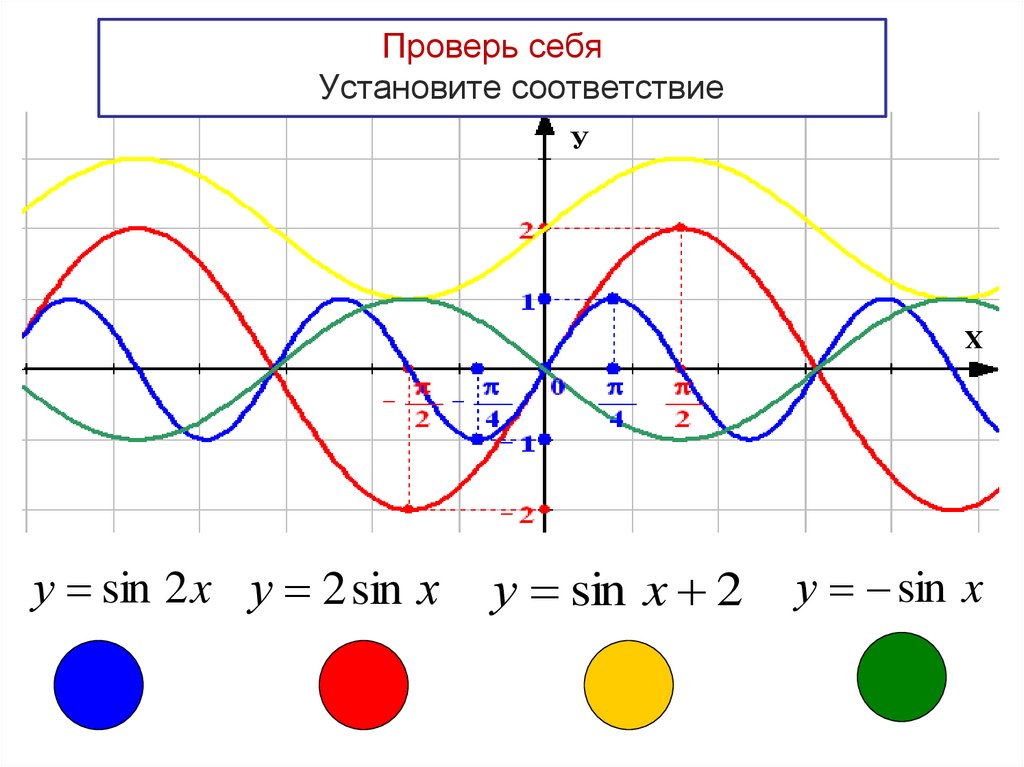
34.
Проверь себяУстановите соответствие
У
Х
у = sin 2 x у = 2 sin х
у = sin x 2
у = sin x
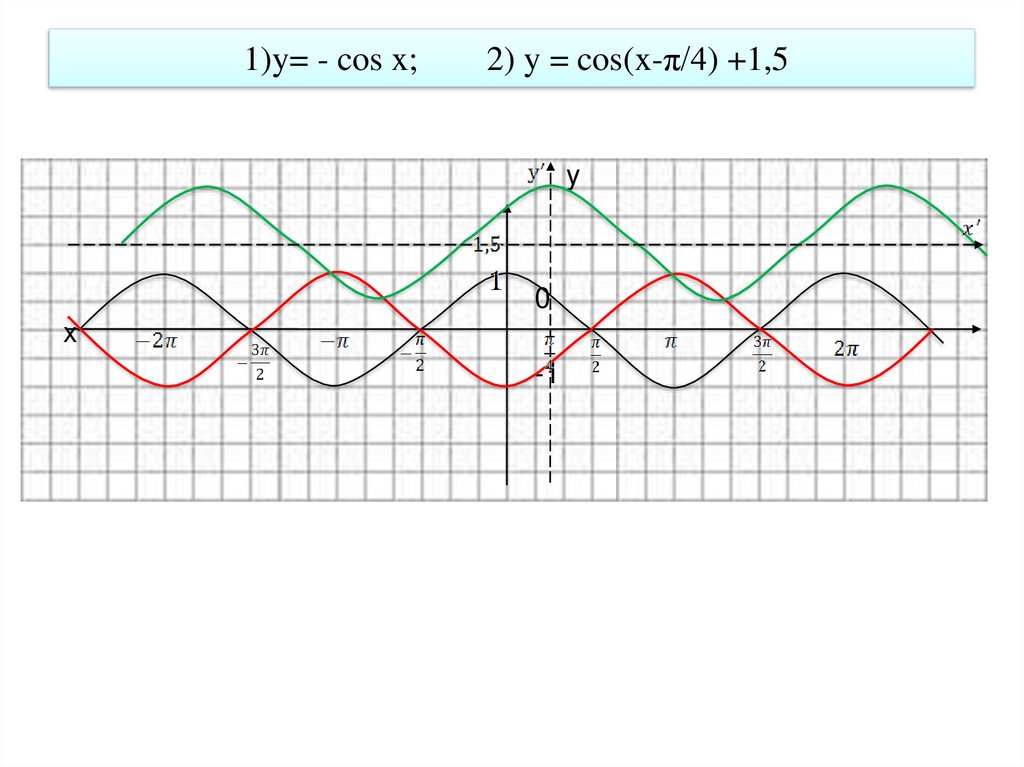
35. 1)y= - cos x; 2) y = cos(x-π/4) +1,5
y0
x
-1
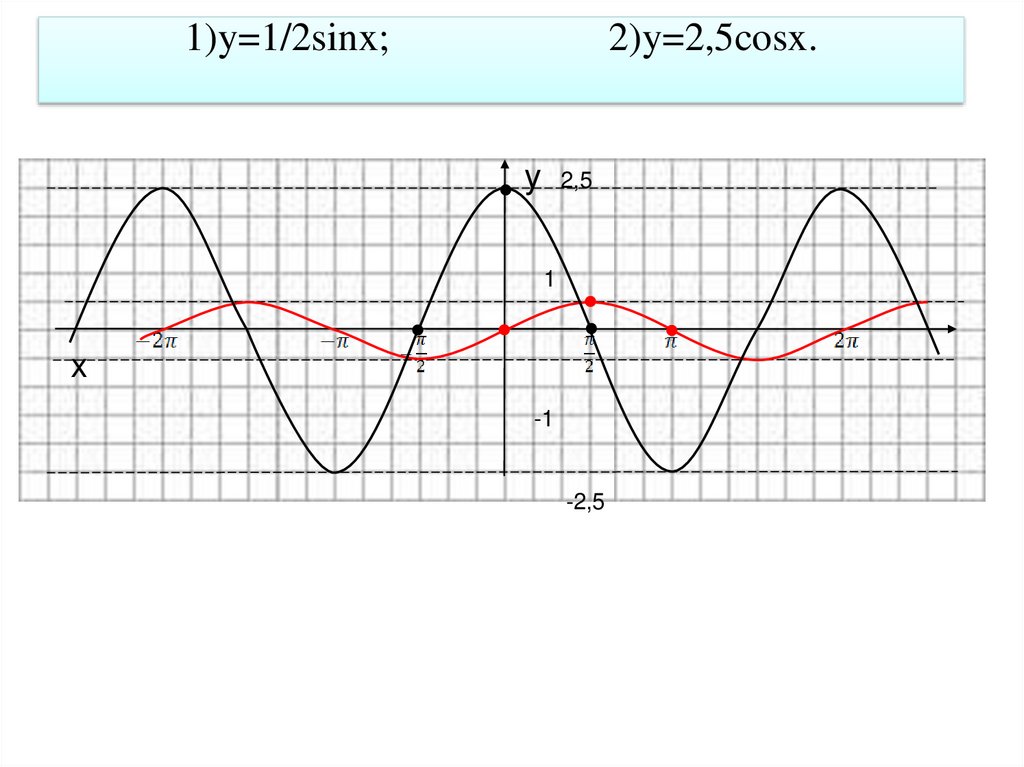
36. 1)y=1/2sinx; 2)y=2,5cosx.
y2,5
1
x
-1
-2,5




 mathematics
mathematics