Задачи на расстояния в пространстве

1.

Расстояния в
пространстве

2.

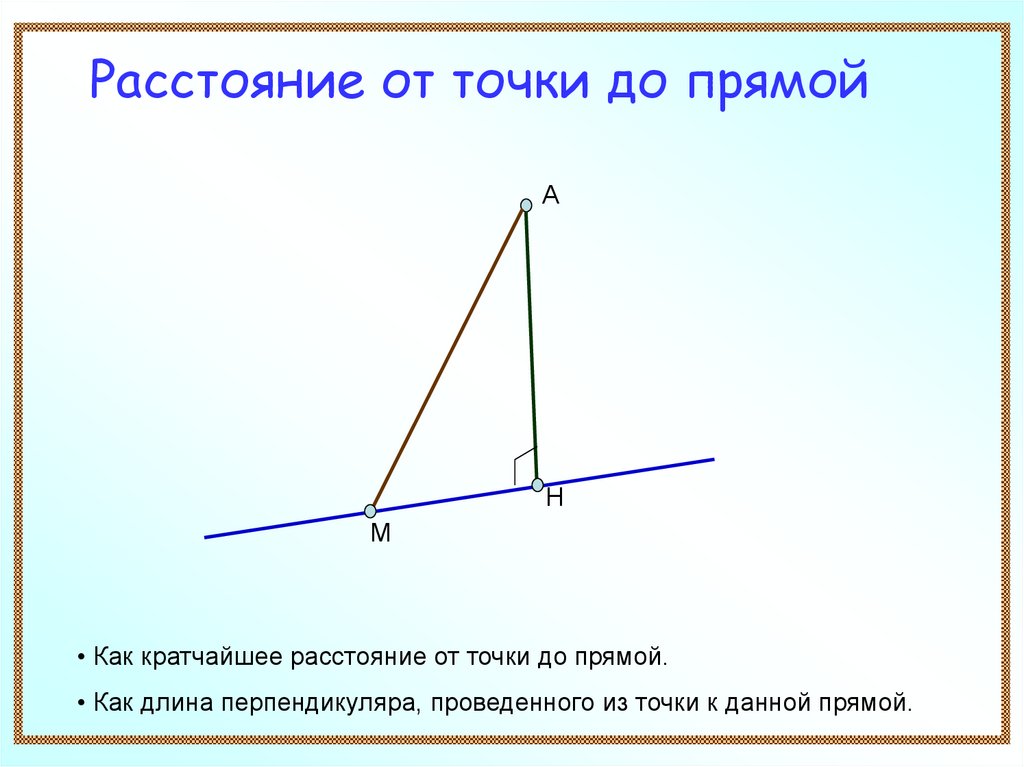
Расстояние от точки до прямой
А
Н
М
• Как кратчайшее расстояние от точки до прямой.
• Как длина перпендикуляра, проведенного из точки к данной прямой.

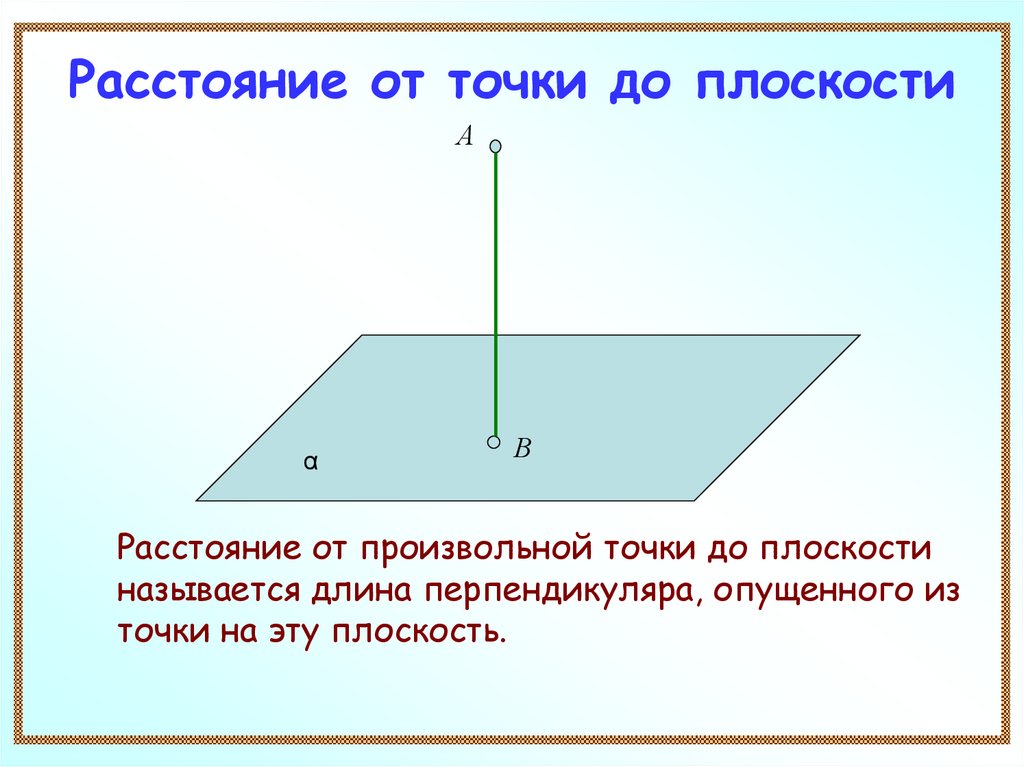
3. Расстояние от точки до плоскости

А
α
В
Расстояние от произвольной точки до плоскости
называется длина перпендикуляра, опущенного из
точки на эту плоскость.

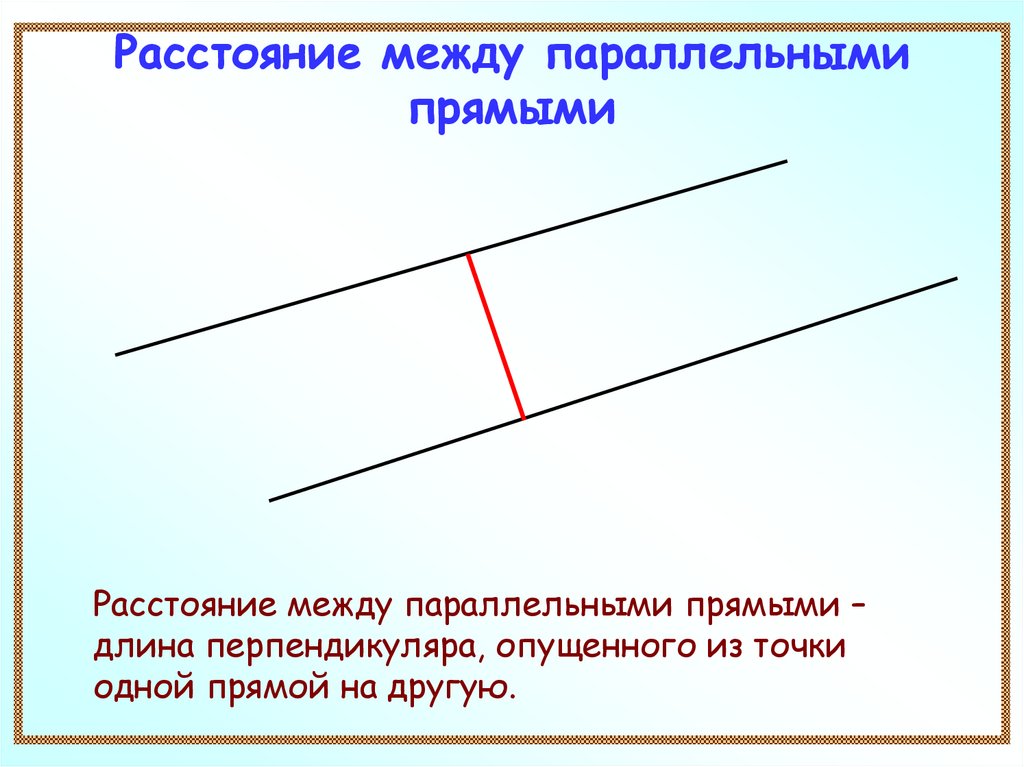
4. Расстояние между параллельными прямыми

Расстояние между параллельными прямыми –
длина перпендикуляра, опущенного из точки
одной прямой на другую.

5.

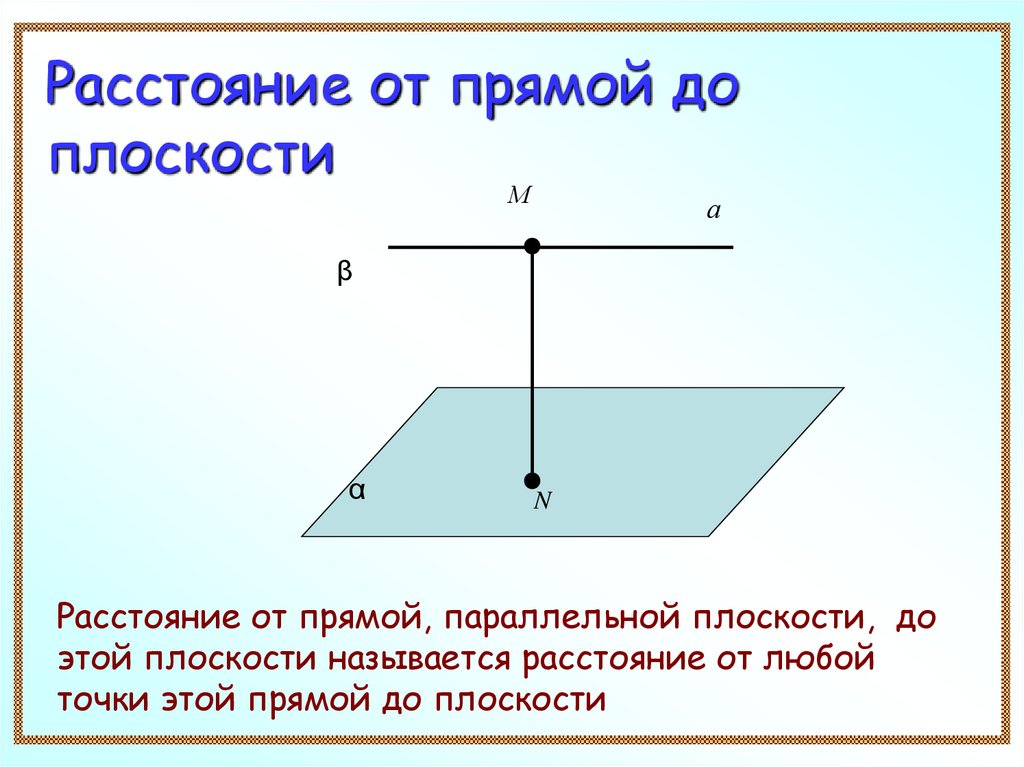
Расстояние от прямой до
плоскости
М
а
β
α
N
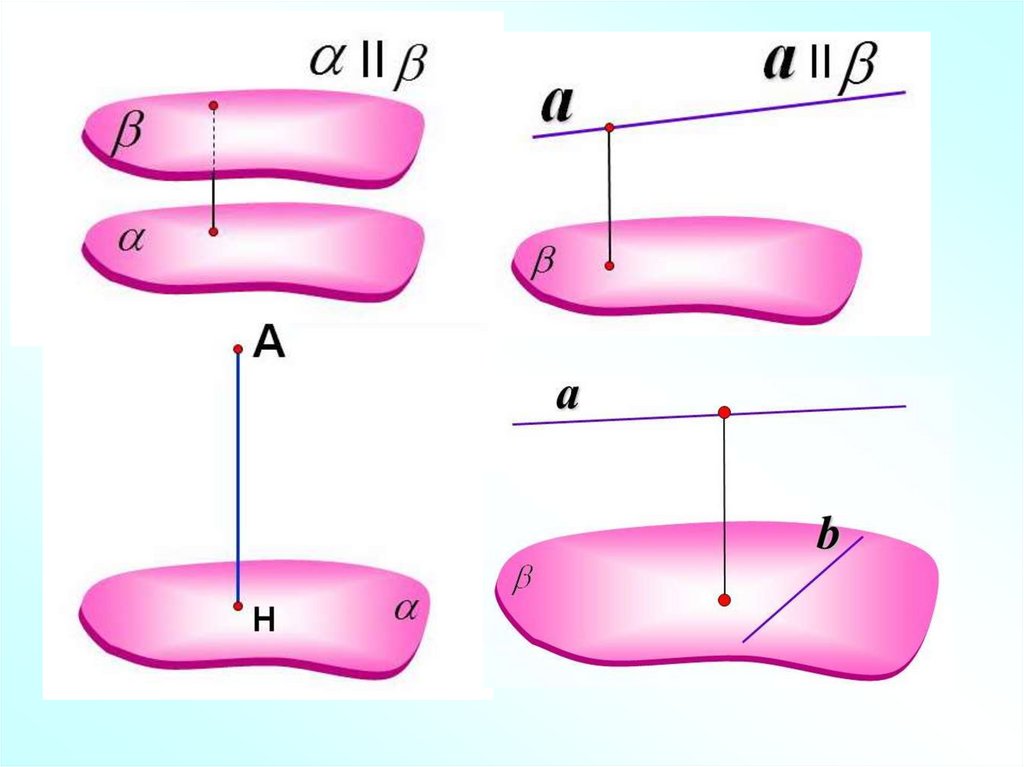
Расстояние от прямой, параллельной плоскости, до
этой плоскости называется расстояние от любой
точки этой прямой до плоскости

6.

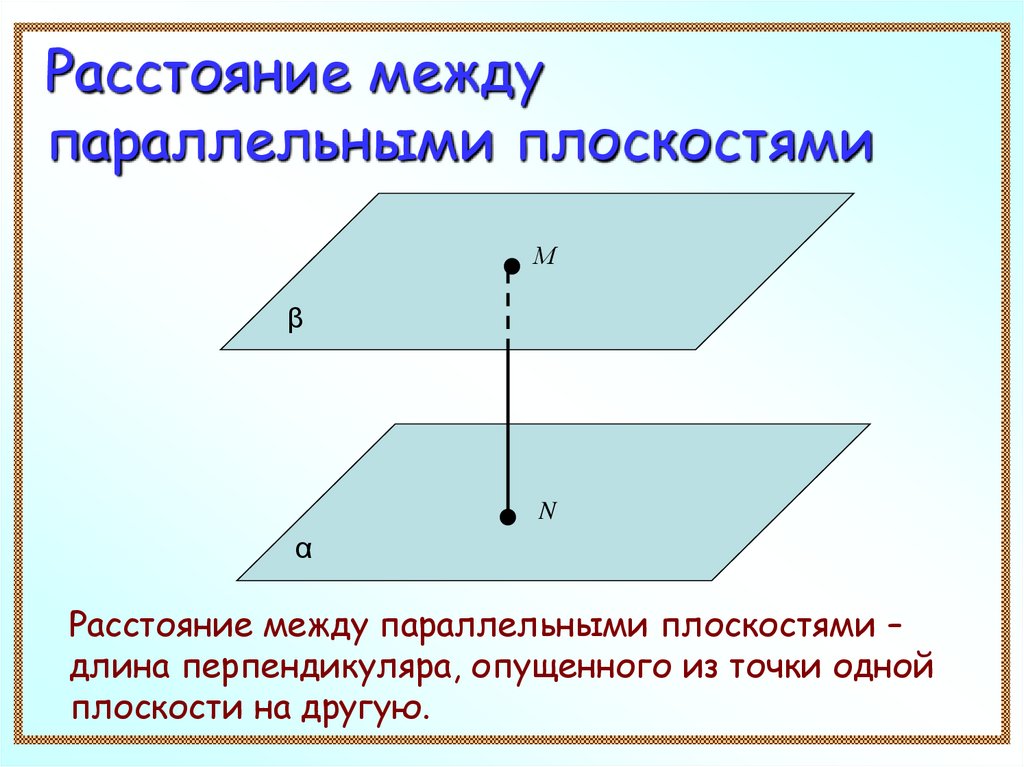
Расстояние между
параллельными плоскостями
М
β
N
α
Расстояние между параллельными плоскостями –
длина перпендикуляра, опущенного из точки одной
плоскости на другую.

7.

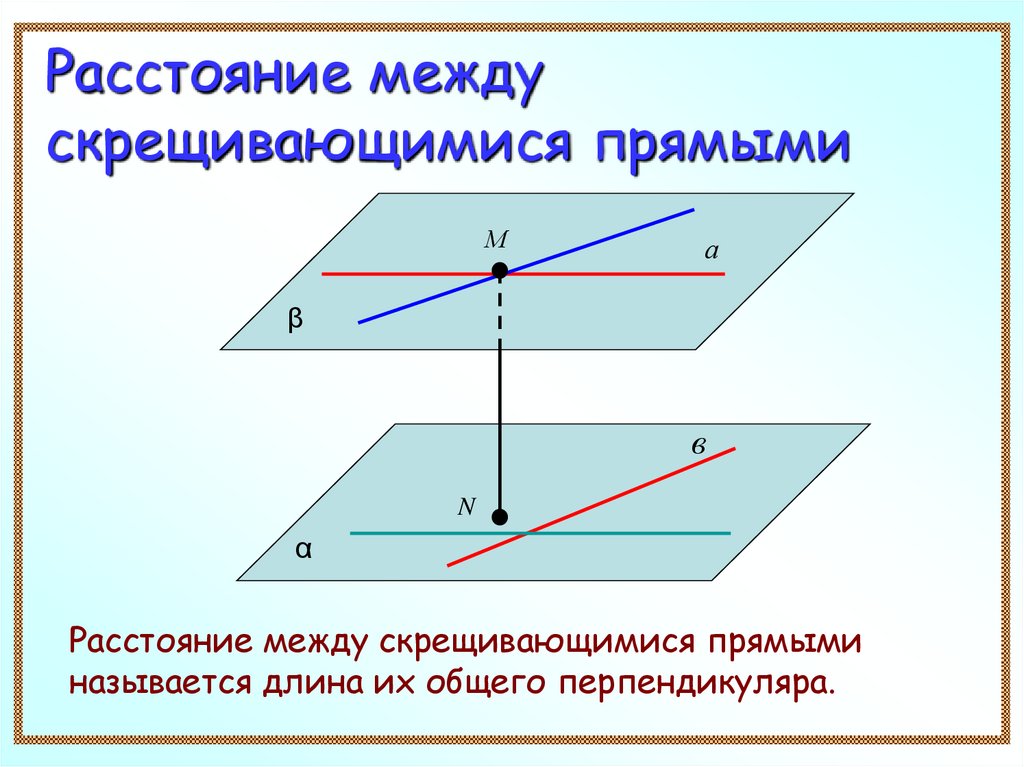
Расстояние между
скрещивающимися прямыми
М
а
β
в
N
α
Расстояние между скрещивающимися прямыми
называется длина их общего перпендикуляра.

8.

Расстояние
Отрезок, имеющий
между одной
концы
изна
скрещивающихся
двух скрещивающихся
прямых и
плоскостью,
прямых и перпендикулярный
проходящей черезкдругую
этим прямым,
прямую называется
параллельно
первой,
их общим
называется
перпендикуляром.
расстоянием между скрещивающимися
прямыми.
На рисунке АВ – общий перпендикуляр.
В
А

9.

10.

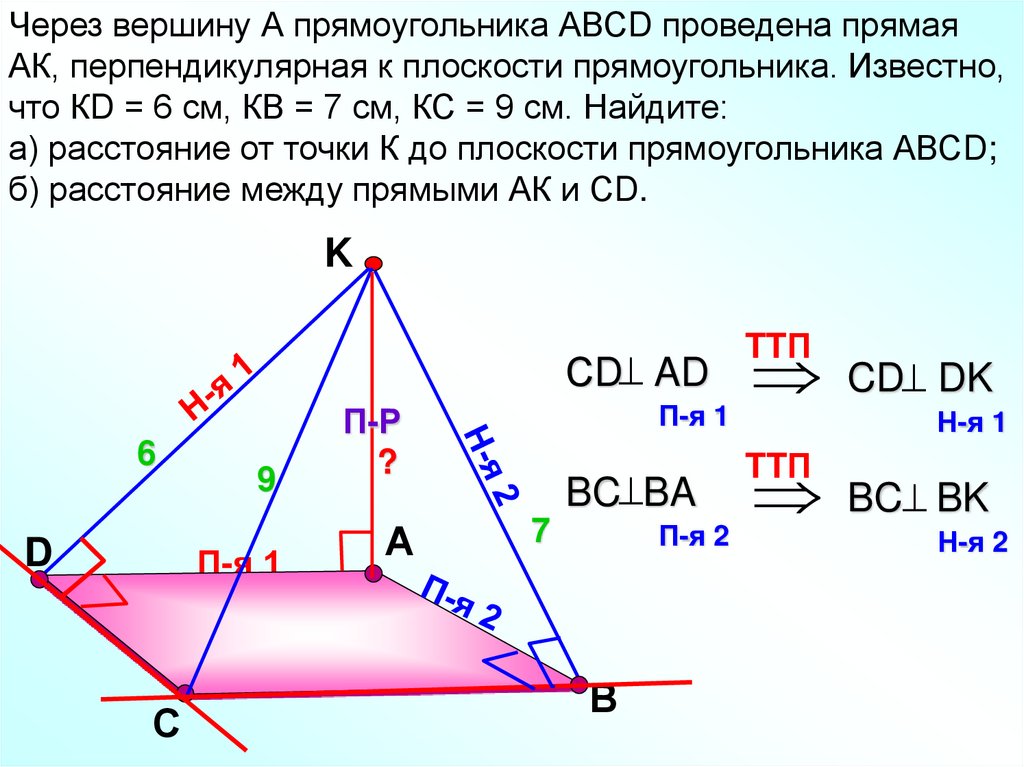
Через вершину А прямоугольника АВСD проведена прямая
АК, перпендикулярная к плоскости прямоугольника. Известно,
что КD = 6 см, КВ = 7 см, КС = 9 см. Найдите:
а) расстояние от точки К до плоскости прямоугольника АВСD;
б) расстояние между прямыми АК и СD.
K
СD AD
6
D
9
П-я 1
С
П-я 1
П-Р
?
А
BC BA
7
П-я 2
В
TTП
CD DK
Н-я 1
TTП
BC BK
Н-я 2

11.

12.

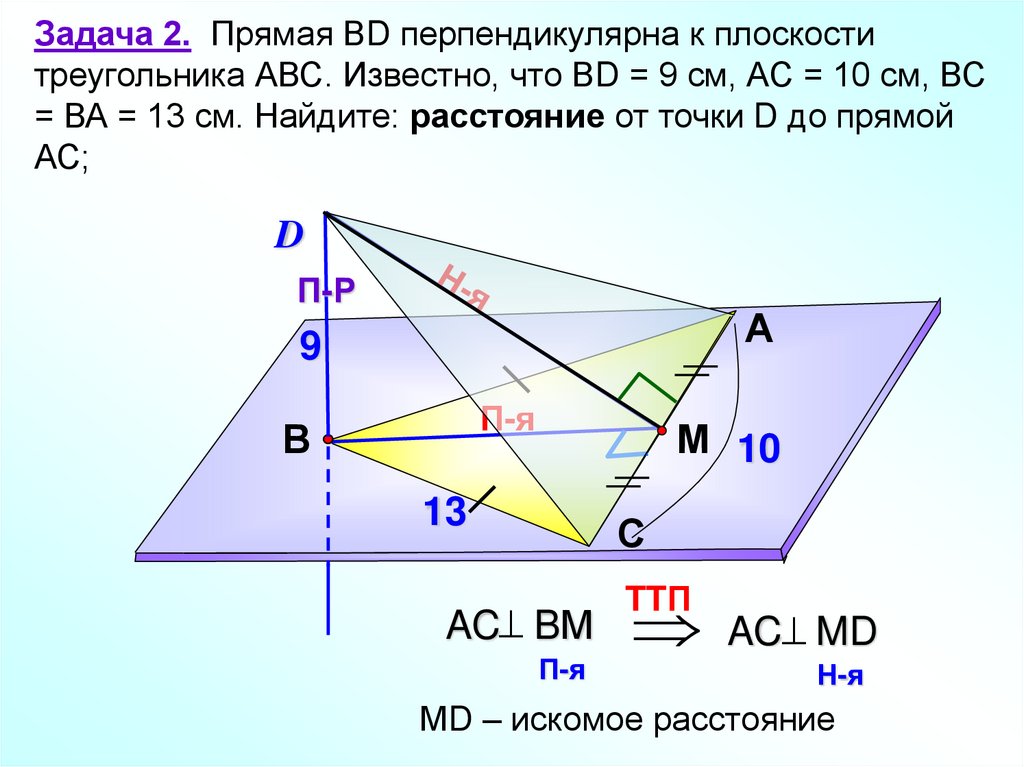
Задача 2. Прямая ВD перпендикулярна к плоскости
треугольника АВС. Известно, что ВD = 9 см, АС = 10 см, ВС
= ВА = 13 см. Найдите: расстояние от точки D до прямой
АС;
D
П-Р
А
9
П-я
В
М 10
13
С
AC BМ
П-я
TTП
AC MD
Н-я
МD – искомое расстояние

13.

14.

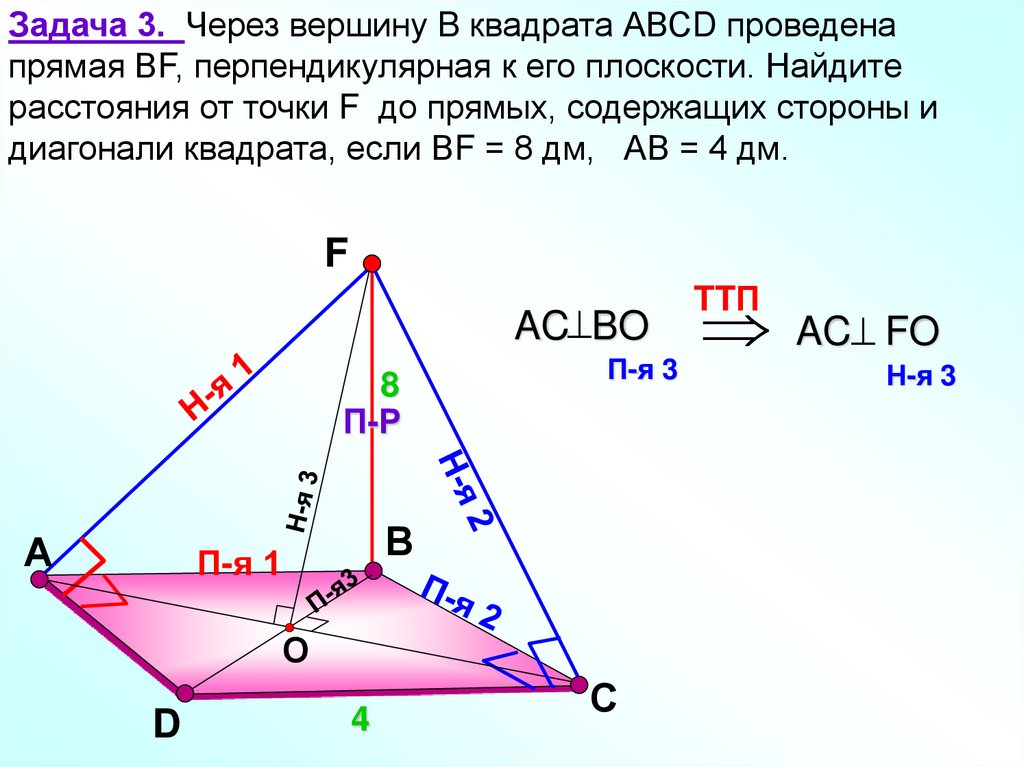
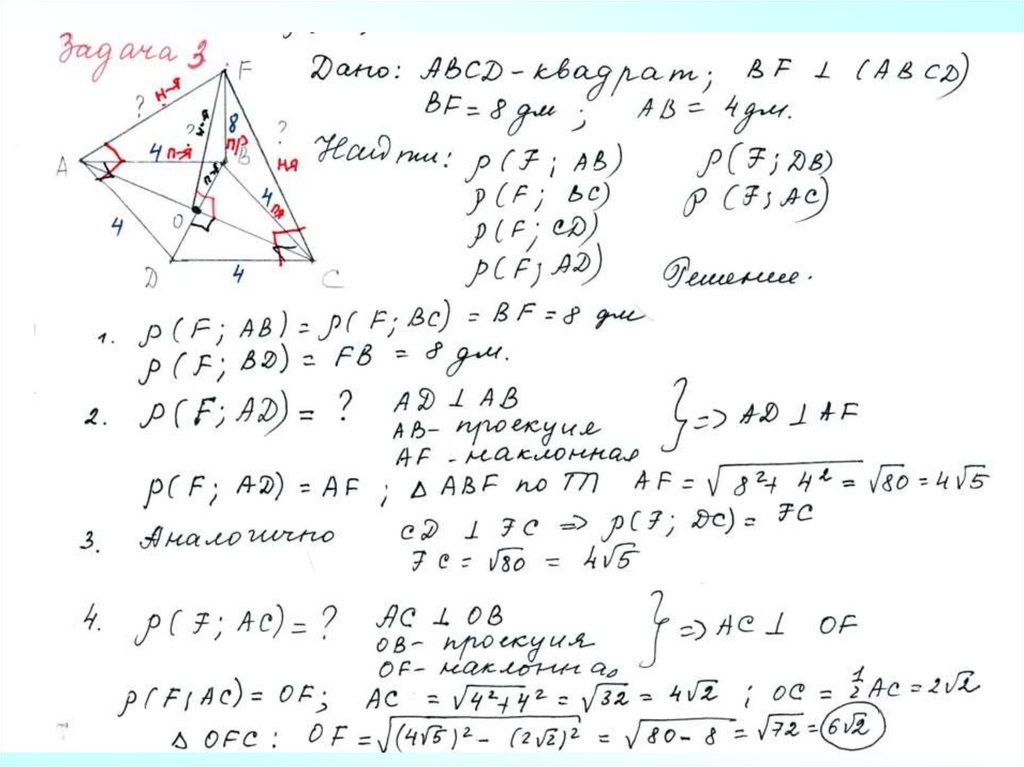
Задача 3. Через вершину B квадрата АВСD проведена
прямая ВF, перпендикулярная к его плоскости. Найдите
расстояния от точки F до прямых, содержащих стороны и
диагонали квадрата, если ВF = 8 дм, АВ = 4 дм.
F
AC BO
8
П-Р
А
П-я 3
В
П-я 1
О
D
4
С
TTП
AC FO
Н-я 3

15.

16.

Через вершину В ромба АВСD проведена прямая ВМ,
перпендикулярная к его плоскости. Найдите расстояние от
точки М до прямых, содержащих стороны ромба, если
АВ = 25 см, ВАD = 600, ВМ = 12,5 см.