Similar presentations:
Тренировочная работа №5 2019-2020. Вариант 1
1. Тренировочная работа №5 2019-2020 Вариант 1
2. 1. Даны числа: B816, 1768, 100110112. Выберите из них то, в двоичной записи которого наибольшее количество единиц. В ответе
запишите выбранное число в десятичной системесчисления.
B816 =101110002
1768 =11111102 =126
100110112
(2 вариант – 184)
3. 2. Логическая функция F задаётся выражением: (x → y) /\ (y ≡ ¬z) /\ (z \/ w). Дан частично заполненный фрагмент, содержащий
неповторяющиесястроки таблицы истинности функции F.
Определите, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Переменная 1 Переменная 2 Переменная 3 Переменная 4 Функция
???
???
???
???
F
1
1
1
1
1
1
1
1
1
xyzwF
00101
0 0 1 1 1 в) w- 2-ой столбец (по 2-ой строке)
0 1 0 1 1 б) y- 1-ый столбец (по «1» в 1-ой и 3-ей
строках)
1 1 0 1 1 а) z- 3-ий столбец (по 3-м «1» в 1-ой строке)
YWZX
(2 вариант – XZWY)
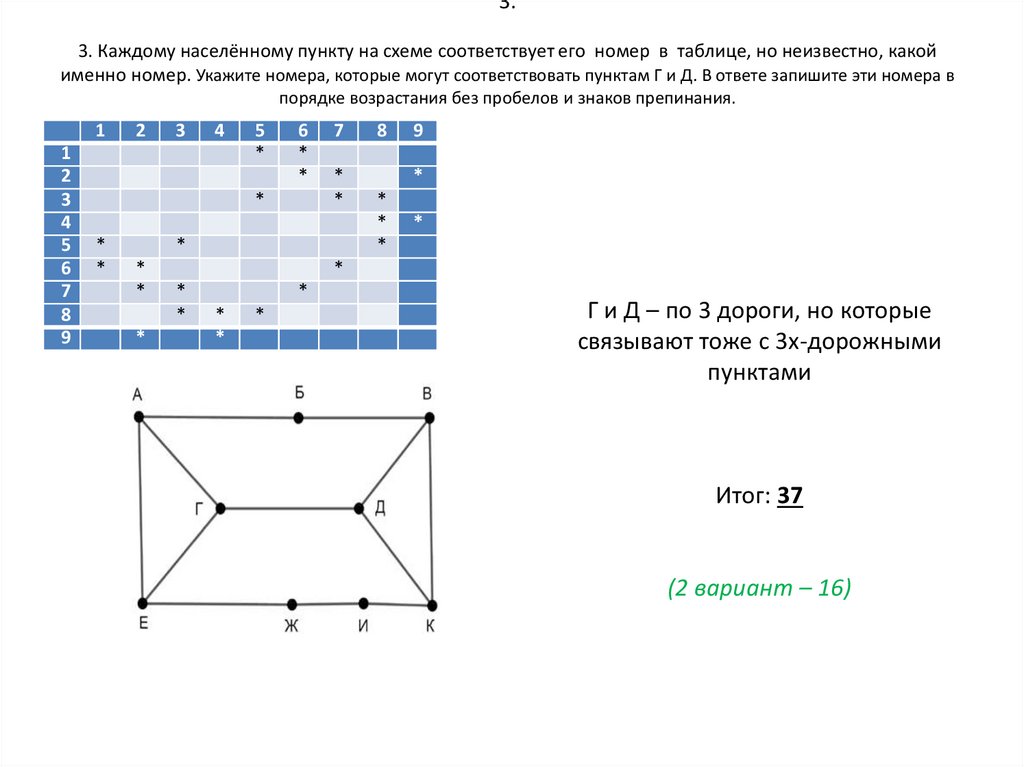
4. 3. 3. Каждому населённому пункту на схеме соответствует его номер в таблице, но неизвестно, какой именно номер. Укажите номера,
которые могут соответствовать пунктам Г и Д. В ответе запишите эти номера впорядке возрастания без пробелов и знаков препинания.
1
1
2
3
4
5
6
7
8
9
2
3
4
5
*
6
*
*
*
*
*
7
*
*
*
*
*
*
8
9
*
*
*
*
*
*
*
*
*
*
*
*
Г и Д – по 3 дороги, но которые
связывают тоже с 3х-дорожными
пунктами
Итог: 37
(2 вариант – 16)
5. 4. На основании имеющихся данных определите ID самой старшей из женщин, у которых первый ребёнок появился до достижения 25
полных лет.Таблица 1
ID Фамилия_И.О.
Пол
Дата
Таблица 2
ID_Родителя
ID_Ребёнка
рождения
162 Горбатко С.И.
Ж
09.05.1968
351
162
169 Горбатко Е.М.
Ж
11.11.2016
717
169
253 Попович П.Н.
М
12.05.1998
394
253
351 Климук А.П.
Ж
13.04.1940
351
394
394 Попович Н.И.
Ж
08.09.1971
844
529
529 Савиных Г.А.
Ж
13.11.2017
949
609
609 Климук Н.П.
Ж
24.08.2015
162
717
717 Горбатко М.И.
М
17.06.1988
351
748
748 Климук О.И.
М
14.07.1965
949
807
807 Климук И.П.
М
01.03.2012
748
844
844 Савиных А.О.
Ж
22.12.1991
966
844
918 Горбатко Н.М.
М
12.04.2018
717
918
949 Климук П.О.
М
19.10.1988
748
949
966 Климук И.С.
Ж
15.02.1966
966
949
…
…
…
…
…
162 (1968) – 717 (1988) V
351 (1940) – 394 (1971) x
748 (1965)
394 (1971) – 253 (1998) х
844 (1991) – 529 (2017) х
966(1966) – 844 (1991) V
949 (1988)
966
(2 вариант – 162)
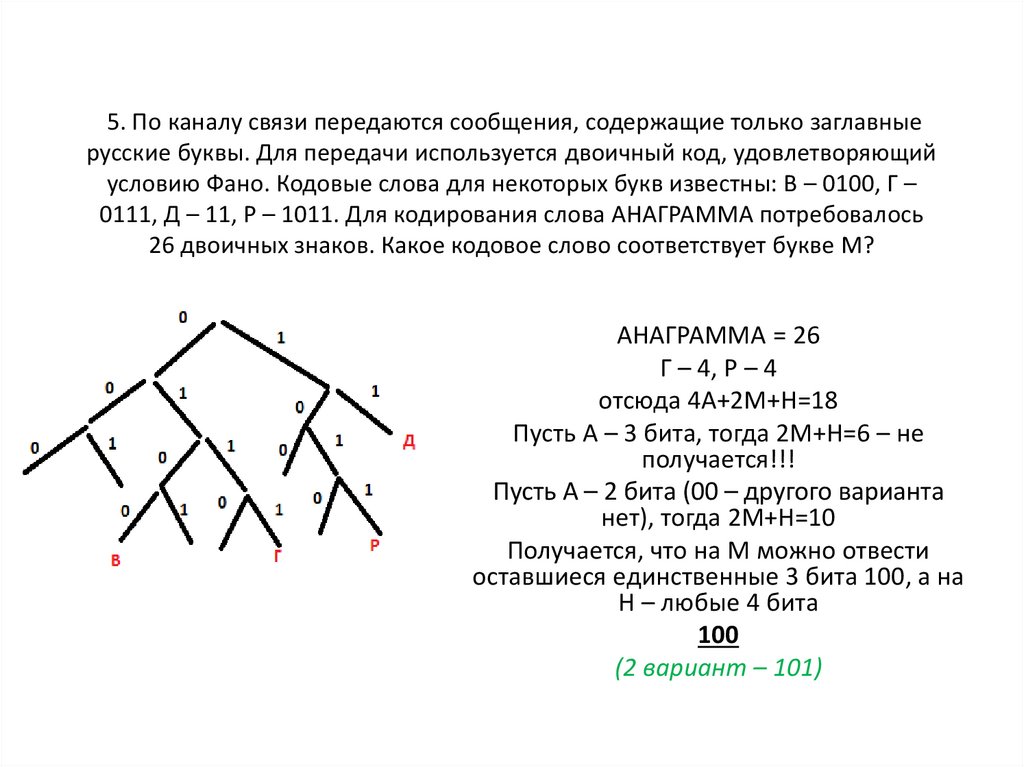
6. 5. По каналу связи передаются сообщения, содержащие только заглавные русские буквы. Для передачи используется двоичный код,
удовлетворяющийусловию Фано. Кодовые слова для некоторых букв известны: В – 0100, Г –
0111, Д – 11, Р – 1011. Для кодирования слова АНАГРАММА потребовалось
26 двоичных знаков. Какое кодовое слово соответствует букве М?
АНАГРАММА = 26
Г – 4, Р – 4
отсюда 4А+2М+Н=18
Пусть А – 3 бита, тогда 2М+Н=6 – не
получается!!!
Пусть А – 2 бита (00 – другого варианта
нет), тогда 2М+Н=10
Получается, что на М можно отвести
оставшиеся единственные 3 бита 100, а на
Н – любые 4 бита
100
(2 вариант – 101)
7. 6. Автомат обрабатывает натуральное число N по следующему алгоритму: Строится двоичная запись числа N. В конец двоичной записи
добавляются две первые цифры этой записи вобратном порядке.
Результат переводится в десятичную систему и выводится на экран.
Пример. Дано число N = 11. Алгоритм работает следующим образом:
Двоичная запись числа N: 1011.
В конец записи добавляются цифры 01 – первые две цифры в обратном порядке
(сначала вторая, затем первая), получается 101101.
На экран выводится число 45.
При каком наименьшем исходном N результат на экране автомата будет больше
90?
91 -10110112 - последние 2 цифры по алгоритму должны быть 01, следовательно
не это число.
92 -10111002 – аналогично не это число
93 -10111012 – последние 2 цифры по алгоритму добавлены верно,
следовательно исходное число 101112 =23
(2 вариант – 19)
8. 7. Дан фрагмент электронной таблицы. В ячейку C3 записали формулу = A4 + $B2. Затем формулу из ячейки C3 скопировали в ячейку
E2. Запишитев ответе сумму числовых значений, показанных в ячейках C3 и E2.
A
B
C
D
E
F
1
10
20
30
40
50
60
2
70
80
90
100
3
400
500
4
1200
1400
1600
300
700
800
900
1800
2000
2200
в С3 1200 + 80 = 1280
в Е2 будет формула
=С3 + $B1=1280 + 20 = 1300
Сумма в С3 и Е2
1300 + 1280 = 2580
(2 вариант - 6200)
9. 8. Запишите число, которое будет напечатано в результате выполнения следующей программы.
var s, n: integer;begin
s := 600;
n := 10;
while s + 2*n >= 400 do begin
s := s - 40;
n := n + 10
end;
writeln(s)
end.
S 600 560 520 480 440 400 360 320 280 240 200 160 120
N 10 20 30 40 50 60 70 80 90 100 110 120 130
120 + 2*130 = 360 < 400
Итог: 120
(2 вариант - 50)
10. 9. Для проведения эксперимента записывается звуковой фрагмент в формате квадро (четырёхканальная запись) с частотой
квадро (четырёхканальная запись) с частотой дискретизации 32 кГц и 32-битнымразрешением. Результаты записываются в файл, сжатие данных не
производится; дополнительно в файл записывается служебная информация,
необходимая для эксперимента, размер полученного файла 97 Мбайт. Затем
производится повторная запись этого же фрагмента в формате моно
(одноканальная запись) с частотой дискретизации 16 кГц и 16-битным
разрешением. Результаты тоже записываются в файл без сжатия и со служебной
информацией, размер полученного файла 7 Мбайт. Объём служебной
информации в обоих случаях одинаков. Укажите этот объём в мегабайтах. В
ответе укажите только число (количество Мбайт), единицу измерения указывать
не надо.
Пусть объем служебной инф-ции - k, время звучания - t
Объем файла квадро: 32000*32*t*4+k = 97*223
Объем файла моно: 16000*16*t +k= 7*223
Из 2-го уравнения t = (7*223 – k)/(16000*16)
Подставим t в 1-ое уравнение: (32000*32*4* (7*223 –
k))/(16000*16) +k = 97*223
Откуда k = 1*223 = 1 Мбайт
(2 вариант – 2)
11. 10. Борис составляет 6-буквенные коды из букв Б, О, Р, И, С. Буквы Б и Р нужно обязательно использовать ровно по одному разу,
букву С можно использоватьодин раз или не использовать совсем, буквы О и И можно использовать
произвольное количество раз или не использовать совсем. Сколько различных
кодов может составить Борис?
В этом задании без
формул комбинаторики
не обойтись – надо
подсчитать количество
размещений n букв на k
местах (количество
перестановок без
повторений):
Akn = n!/(n-k)!
(2 вариант – 1080)
1)Если буквы С нет вообще, то
сколько вариантов размещения букв
БиР
A26 = 6!/(6-2)! = 30
Один из таких вариантов
Б Р 2 2 22
2*2*2*2 = 16, но т.к. вариантов всего
30, то 30*16=480
2)Если буква С есть, то вариантов
размещения букв С, Р и Б
A36 = 6!/(6-3)! = 120
Один из таких вариантов
Б Р С 2 22
2*2*2 = 8, но т.к. вариантов всего
120, то 120*8=960
Итого 480 + 960 = 1440
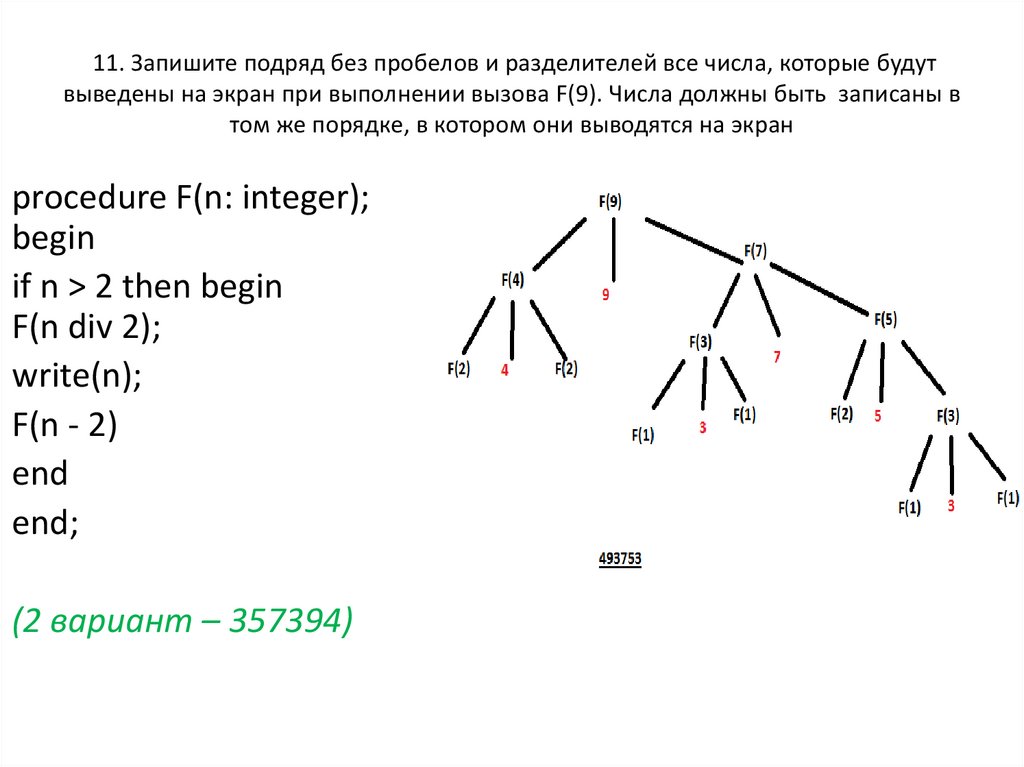
12. 11. Запишите подряд без пробелов и разделителей все числа, которые будут выведены на экран при выполнении вызова F(9). Числа
должны быть записаны втом же порядке, в котором они выводятся на экран
procedure F(n: integer);
begin
if n > 2 then begin
F(n div 2);
write(n);
F(n - 2)
end
end;
(2 вариант – 357394)
procedure F(n: integer);
begin
if n > 0 then begin
write(n);
F(n - 3);
F(n div 2) end
end;
13. 12. В терминологии сетей TCP/IP маской сети называется двоичное число, определяющее, какая часть IP-адреса узла сети относится
к адресу сети, акакая – к адресу самого узла в этой сети. При этом в маске сначала (в
старших разрядах) стоят единицы, а затем с некоторого места – нули. Обычно
маска записывается по тем же правилам, что и IP-адрес, – в виде четырёх байтов,
причём каждый байт записывается в виде десятичного числа. Адрес сети
получается в результате применения поразрядной конъюнкции к заданному IPадресу узла и маске. Например, если IP-адрес узла равен 231.32.255.131, а маска
равна 255.255.240.0, то адрес сети равен 231.32.240.0.
Для узла с IP-адресом 132.214.141.28 адрес сети равен 132.214.141.0. Укажите
наибольшее возможное значение последнего (самого правого) байта маски этой
сети. Ответ запишите в виде десятичного числа.
IP
2810= 000111002
сеть 010= 000000002
Несовпадение начинается с 4-го слева
разряда, следовательно с этого разряда
маска нулевая, т.е 111000002= 224
(2 вариант – 192)
14. 13. При регистрации на сервере каждый пользователь получает уникальный персональный код, состоящий из 21 символа, каждый из
которых может бытьодной из 26 заглавных латинских букв. При этом в базе данных сервера
формируется запись, содержащая этот код и дополнительную информацию о
пользователе. Для представления кода используют посимвольное кодирование,
все символы кодируют одинаковым минимально возможным количеством бит, а
для кода в целом выделяется минимально возможное целое количество байт.
Для хранения данных о 40 пользователях потребовалось 2400 байт. Сколько байт
выделено для хранения дополнительной информации об одном пользователе? В
ответе запишите только целое число – количество байт.
• 25>26 5 бит/символ
• 5*21=105 бит/код = 14 байт/код
• 2400 / 40 = 60 байта/пользователь
• 60 – 14 = 46 байт на допол. Сведения
(2 вариант – 29)
15. 14. Исполнитель Редактор получает на вход строку цифр и преобразует её. Известно, что исходная строка начинается с цифры 0, а
далее содержит12 цифр 1, 15 цифр 2 и 17 цифр 3, расположенных в произвольном порядке. Сколько цифр 2
будет в строке, которая получится после выполнения данной программы?
НАЧАЛО
ПОКА нашлось (01) ИЛИ нашлось (02)
ИЛИ нашлось (03)
заменить (01, 103)
заменить (02, 10)
заменить (03, 210)
КОНЕЦ ПОКА
КОНЕЦ
Т.е.
01 -> 103
02 -> 10
03 -> 210
(2 вариант – 32)
0111….11(12)222…….2(15)33……..33(17)
в произвольном порядке
Пусть в начале стоят 11……..1:
1031…..1(11)2………2(15)3……….3(17)
12101….1(11)2………2(15)3……….3(17)
1211031..1(10)2………2(15)3……….3(17
И т.д.
121121…121(12)02…2(15)3……….3(17)
121121…121(12)102…2(14)3……….3(17)
И т.д.
121121…121(12)11…1(15)03……….3(17)
121121…121(12)11…1(15)2103……3(16)
И т.д.
121121…121(12)11…1(15)21……….21(17)0
Больше цикл не выполняется.
12 + 17 = 29
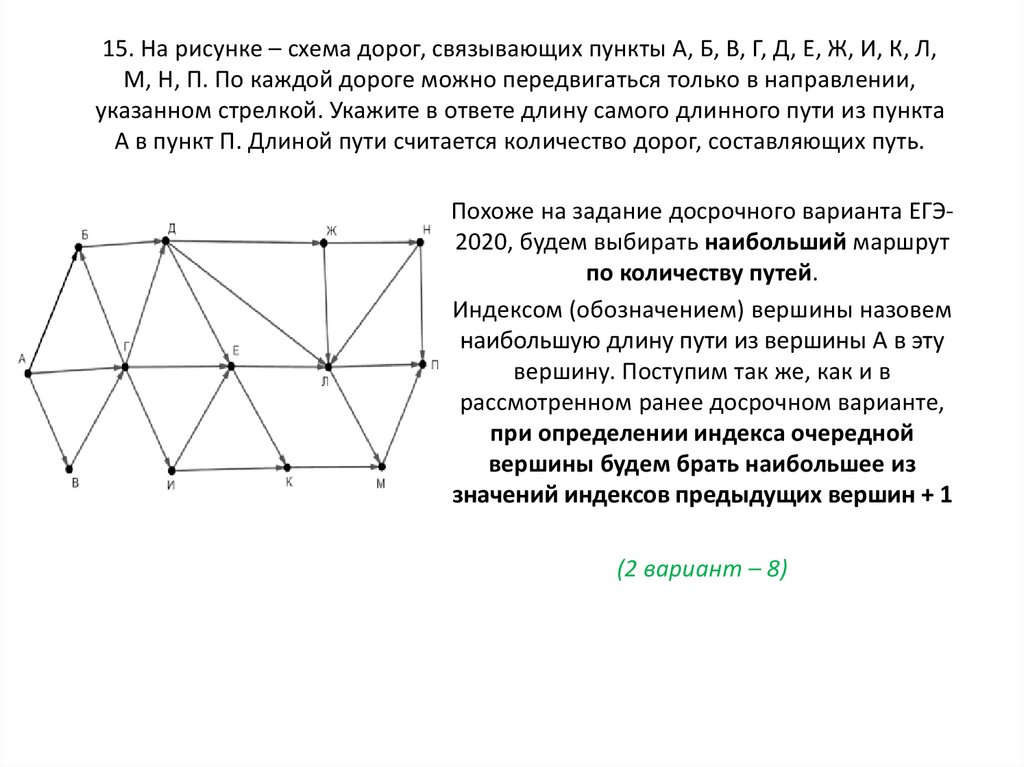
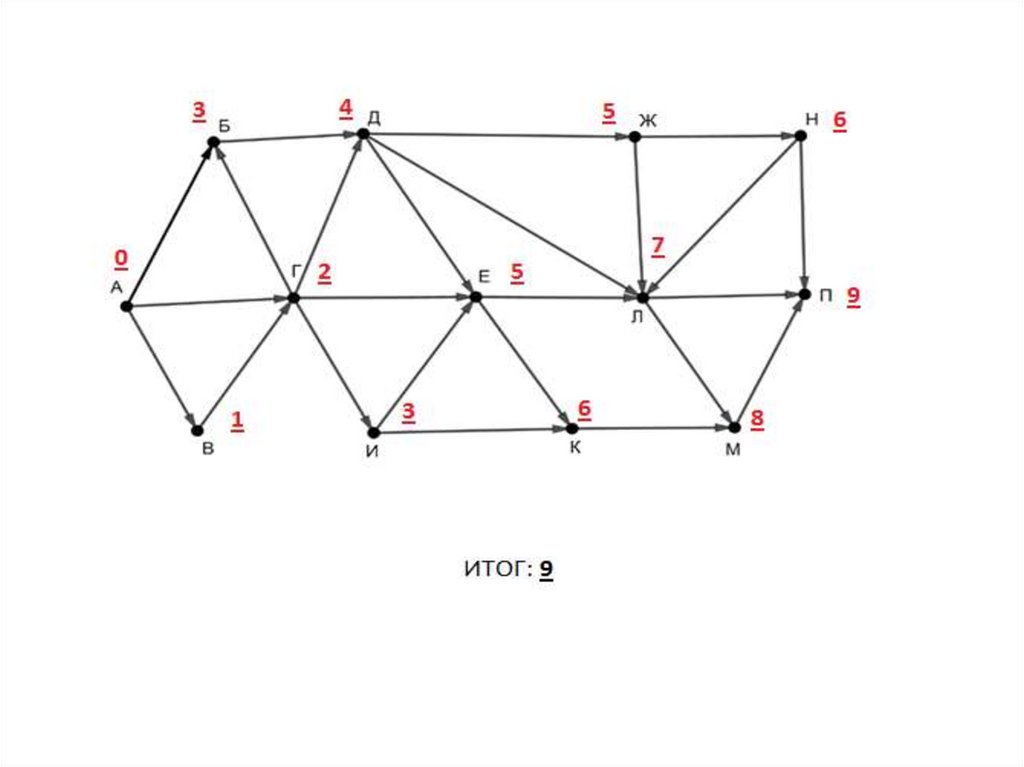
16. 15. На рисунке – схема дорог, связывающих пункты А, Б, В, Г, Д, Е, Ж, И, К, Л, М, Н, П. По каждой дороге можно передвигаться
только в направлении,указанном стрелкой. Укажите в ответе длину самого длинного пути из пункта
А в пункт П. Длиной пути считается количество дорог, составляющих путь.
Похоже на задание досрочного варианта ЕГЭ2020, будем выбирать наибольший маршрут
по количеству путей.
Индексом (обозначением) вершины назовем
наибольшую длину пути из вершины А в эту
вершину. Поступим так же, как и в
рассмотренном ранее досрочном варианте,
при определении индекса очередной
вершины будем брать наибольшее из
значений индексов предыдущих вершин + 1
(2 вариант – 8)
17.
18. 16. Значение выражения 497 × 720 – 78 – 28 записали в системе счисления с основанием 7. Сколько цифр 6 содержится в этой
16. Значение выражения 497 × 720 – 78 – 28 записаливсистеме
счисления с основанием 7. Сколько цифр 6 содержится в этой записи?
Вспомним формулы для любой системы счисления:
число aN в системе счисления с основанием a записывается как
единица и N нулей:
число aN-1 в системе счисления с основанием a записывается как N
старших цифр этой системы счисления, то есть, цифр (a-1):
число aN – aM = aM · (aN-M – 1) записывается в системе счисления с
основанием a как N-M старших цифр этой системы счисления, за
которыми стоят M нулей:
19.
497×720 – 78 – 28 = 714×720 – 78 – 4×71 =734 – 78 – 4×71
Из-за того, что в формуле 2 элемента со знаком минус, не получится
обойтись только формулами.
Если рассмотреть 734 – 78, то в этом выражении по формулам 34-8=26 «6»
и 8 «0». Вычитание же из этого 4×71 (т.е. 406) изменяет количество «6»:
6…………600000000
26
40
6………..6566666630
25
Итого: 25 + 6 = 31
(2 вариант – 28)
20. 17. В таблице приведены запросы и количество найденных по ним страниц некоторого сегмента сети Интернет. Какое количество
страниц (в тысячах) будет найдено по запросуСемёновский | Преображенский | Борменталь?
Запрос
Семёновский
Преображенский
Борменталь
Преображенский | Борменталь
Преображенский &
Семёновский
Семёновский | Борменталь
Найдено страниц (в тысячах)
136
318
93
331
92
229
Сразу заметим, что у множеств Семеновский и Борменталь нет ни одной общей
точки
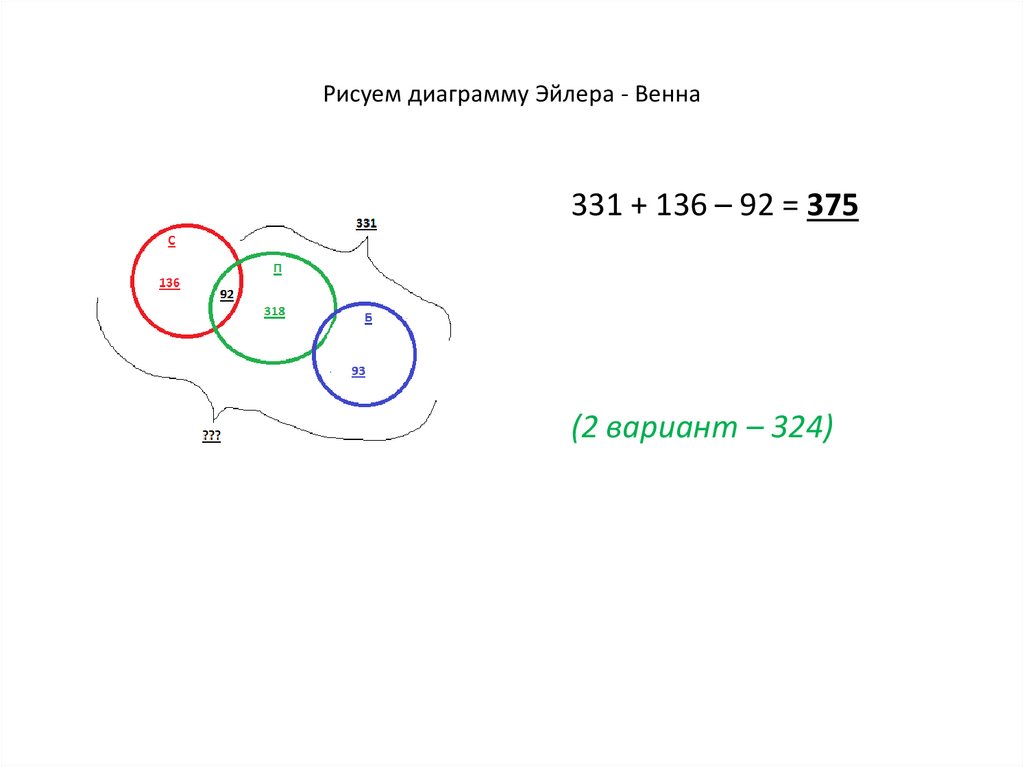
21. Рисуем диаграмму Эйлера - Венна
331 + 136 – 92 = 375(2 вариант – 324)
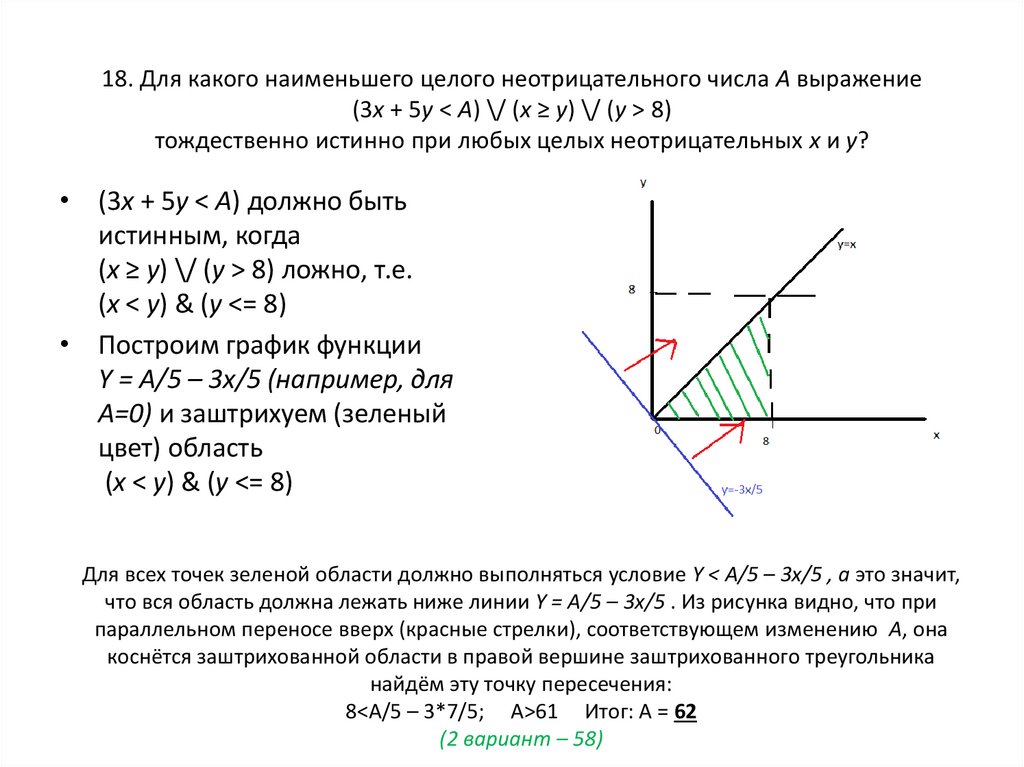
22. 18. Для какого наименьшего целого неотрицательного числа A выражение (3x + 5y < A) \/ (x ≥ у) \/ (y > 8) тождественно истинно
18. Для какого наименьшего целого неотрицательного числа A выражение(3x + 5y < A) \/ (x ≥ у) \/ (y > 8)
тождественно истинно при любых целых неотрицательных x и y?
• (3x + 5y < A) должно быть
истинным, когда
(x ≥ у) \/ (y > 8) ложно, т.е.
(x < y) & (y <= 8)
• Построим график функции
Y = A/5 – 3x/5 (например, для
А=0) и заштрихуем (зеленый
цвет) область
(x < y) & (y <= 8)
Для всех точек зеленой области должно выполняться условие Y < A/5 – 3x/5 , а это значит,
что вся область должна лежать ниже линии Y = A/5 – 3x/5 . Из рисунка видно, что при
параллельном переносе вверх (красные стрелки), соответствующем изменению A, она
коснётся заштрихованной области в правой вершине заштрихованного треугольника
найдём эту точку пересечения:
8<A/5 – 3*7/5; A>61 Итог: А = 62
(2 вариант – 58)
23. 19. Представленный ниже на пяти языках программирования фрагмент программы обрабатывает элементы одномерного целочисленного
массива A с индексами от 0 до 10. Значения элементов массивадо начала выполнения фрагмента представлены в таблице. Определите значение переменной s после
выполнения фрагмента.
k
0 1 2 3
4
5 6 7 8 9 10
A[k] 3 5 8 12 11 5 7 2 9 6 11
19
24 48
s := 0;
n := 6;
for k:=1 to 10 do begin
if s < A[n] then
s := s + A[k] else
A[n] := A[n] + A[k]
end;
s = 0 + 5 + 8 + 11 + 2 + 9 +
6 + 11 = 52
(2 вариант – 53)
24. 20. Ниже на пяти языках программирования записана программа, которая вводит натуральное число x, выполняет преобразования, а
затем выводит два числа.Укажите наименьшее возможное значение x, при вводе которого программа
выведет числа 14 и 24.
var x, a, b: integer;
begin
readln(x);
a := 0; b := 1;
while x > 0 do begin
a := a + x mod 8;
if x mod 2 = 0 then
b := b * (x mod 8);
x := x div 8
end;
writeln(a); write(b)
end.
а – сумма цифр в 8 сс (14)
b – произведение четных цифр
в 8 сс (24)
В 8 сс есть цифры 01234567,
отсюда произведение состоит
из цифр 4*6=24
Поскольку сумма цифр в 8 сс
14, то на оставшиеся цифры 14
– (4+6) = 4, при этом сюда
входят нечетные цифры, т.е. 1 и
3
Поскольку надо наименьшее
число, то 13468 = 742
(2 вариант – 670)
25. 21. Сколько существует различных целых положительных значений k, при вводе которых программа выводит тот же ответ, что и при k
= 15? Значение k = 15 тоже учитывается.var i, k : integer;
function f(n: integer): integer;
begin
f := n * n * n
end;
function g(n: integer): integer;
begin
g := 2*n*n + 5
end;
begin
readln(k); i := 1;
while f(i) < g(k) do i := i+1;
writeln(i)
end.
(2 вариант – 3)
сначала заметим, что функция f возвращает куб
переданного ей числа, а функция g – результат
вычисления 2*n*n+5
при некотором i работа цикла останавливается:
это происходит при нарушении условия
f(i)<g(k), то есть при выполнении обратного
условия f(i) g(k)
в то же время на предыдущем шаге цикла (для i1) условие его работы выполнялось, то есть
f(i-1)<g(k), откуда получаем
f(i-1)<g(k) f(i)
вспоминая, что f(i)=i3, делаем вывод, что g(k)
должно быть между кубами двух соседних чисел:
(i-1)3 < g(k) i3
для заданного k=15 находим g(15)=2·225+5=455,
так что i=8:
(7)3 < g(k)=455 83
осталось проверить, при каких k выполняется
условие
343 < g(k)=2k2+5 512
решая двойное неравенство относительно k
получаем
13 < k 15,9
таким образом, существует 2 целых числа (14 и
15), удовлетворяющих условию задачи
Итог: 2
26. 22. Исполнитель РазДва преобразует число на экране. У исполнителя есть две команды, которым присвоены номера: Прибавить 1
Умножить на 2Первая команда увеличивает число на экране на 1, вторая умножает его на 2.
Программа для исполнителя РазДва – это последовательность команд. Сколько
существует программ, которые преобразуют исходное число 1 в число 20, и
при этом траектория вычислений содержит ровно одно из чисел 9 и 10?
Траектория вычислений – это последовательность результатов выполнения всех
команд программы. Например, для программы 212 при исходном числе 4
траектория будет состоять из чисел 8, 10, 20.
.
Запишем рекурсивные формулы
по условию:
KN=KN-1+K N div 2 (если число кратно 2)
KN=KN-1 (если число не кратно 2)
По этим формулам заполним сначала таблицу для
траектории, содержащей число 9
N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
KN 1 2 2 4 4 6 6 10 10 0 0 ………………………. 0 10 10 10
0
27.
По этим же формулам заполним теперь таблицу длятраектории, содержащей число 10
N 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20
KN 1 2 2 4 4 6 6 10 0 4 4 ………………………. 4 4 4 8
0
Итого: 10 + 8 = 18
(2 вариант – 13)
28. 23. Сколько существует различных наборов значений логических переменных x1, x2, …, x8, которые удовлетворяют всем перечисленным
ниже условиям?(x1 /\ x2) → (x3 ≡ x4) = 1
(x3 /\ x4) → (x5 ≡ x6) = 1
(x5 /\ x6) → (x7 ≡ x8) = 1
В ответе не нужно перечислять все различные наборы значений переменных x1, x2, …, x8, при которых
выполнена данная система равенств. В качестве ответа Вам нужно указать количество таких наборов.
Поскольку в задании дано 3 подобных уравнения,
будем решать методом отображений:
1-ое из подобных уравнений имеет следующие
решения:
х1 х2 x3 x4 f
0 0 0 0 1
0 0 0 1 1
0 0 1 0 1
0 0 1 1 1
0 1 0 0 1
0 1 0 1 1
0 1 1 0 1
0 1 1 1 1
1 0 0 0 1
1 0 0 1 1
1 0 1 0 1
1 0 1 1 1
1 1 0 0 1
1 1 1 1 1
Изобразим отображение х1x2 на х3x4 (получили
вот такое дерево)
Запишем это формулами:
f(00)=f(00)+f(01)+f(10)+f(11)
f(01)= f(00)+f(01)+f(10)
f(10)= f(00)+f(01)+f(10)
f(11)=f(00)+f(01)+f(10)+f(11)
Для всех остальных уравнений формулы будут
такие же.
29.
f(00)=f(00)+f(01)+f(10)+f(11)f(01)= f(00)+f(01)+f(10)
f(10)= f(00)+f(01)+f(10)
f(11)=f(00)+f(01)+f(10)+f(11)
Заполним таблицу решений по формулам:
х1x2 х3x4 х5x6 х7x8
00
1
4
14
48
01
1
3
10
34
10
1
3
10
34
11
1
4
14
48
Итого по последнему столбцу 48*2+34*2= 164






















 mathematics
mathematics








