Решение тригонометрического уравнения (С 1, 28)

1.

а). Решите уравнение
2 sin х cos х
2
2
б). Найдите все корни этого уравнения, принадлежащие отрезку
2 cos х cos х 0
2
cos х 2 cos х 1 0
cos х 0
2 cos х 1 0
5
;
Применим формулу приведения:
2
Название «синус»
изменится на
«косинус», т.к.
2
sin x cos х
2
2
О четверти и о знаке не думаем,
1 2
т.к. синусиррационал
в квадрате. ьность
х n cos х
(исключим
2 2 2
2
3
2
arccos
arccos
будет
2 2
2 удобно4езаписать
вНам
знаменател
) 4
cos х
решение в виде двух множеств, т.к.
2
аналитическая запись ответа
2
в2виде:
х arccos
n
2
3 3
3 неудобна для
х х
2 n 2х n
; решения
2 n двойного неравенства.
4
4
4

2.

Отбор корней с помощью решения неравенств
5
;
б). Найдите все корни этого уравнения, принадлежащие отрезку
2
n=-1
х
5
2
2
n=-2
n=-3
n
:
5 1
1
n 1
2 2
2
1
3 n 1
2
3
n 2, x
2
5
n 3, x
2
3
х
2 n
4
:
:
3
х
2 n
4
5
5
2
2
5
3
5 33
3
2n
1 2n 1
2
4
2 44
4
13
3
7
1
:2
2n :22n 1
4
4
44
7
1 13 n 7
n
8
8
8 8
5
n 1, x
n Z
4
нет значений

3.

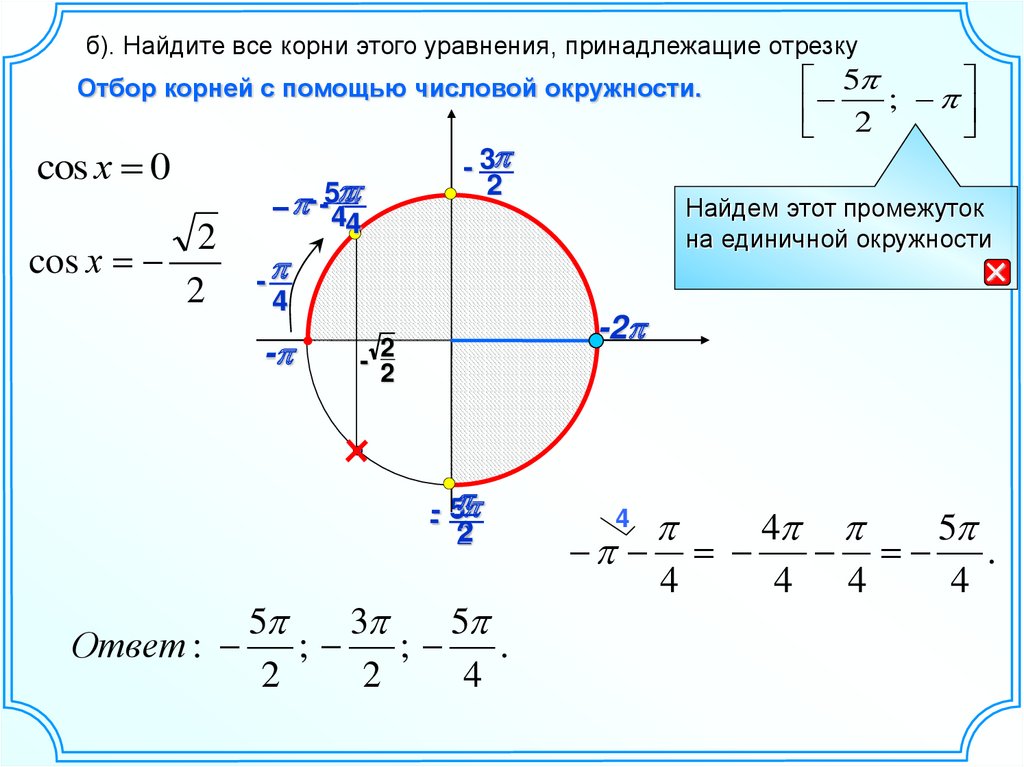
б). Найдите все корни этого уравнения, принадлежащие отрезку
Отбор корней с помощью числовой окружности.
cos х 0
2
cos х
2
– - -54
4
- 3
2
Найдем этот промежуток
на единичной окружности
-
4
-
5
;
2
-2
- 2
2
-- 5
2
5
3
5
Ответ :
;
;
.
2
4
2
4
5
.
4
4 4
4
4