Similar presentations:
Решение тригонометрического уравнения (С 1, 26)
1.
sin х cos 2 ха). Решите уравнение
б). Найдите все корни этого уравнения, принадлежащие отрезку
7p
2
p
;
2
Найдем ОДЗ для уравнения (область допустимых значений уравнения)
sin х 0
p
2
p
0
p
sin х 0
cos 2х 0
cos 2х 0
2pn 2 х
p
4
pn х
p
2
p
4
2pn : 2
pn
p
n – нечет.
n – чет.
0
0
Для аргумента 2х
х
2.
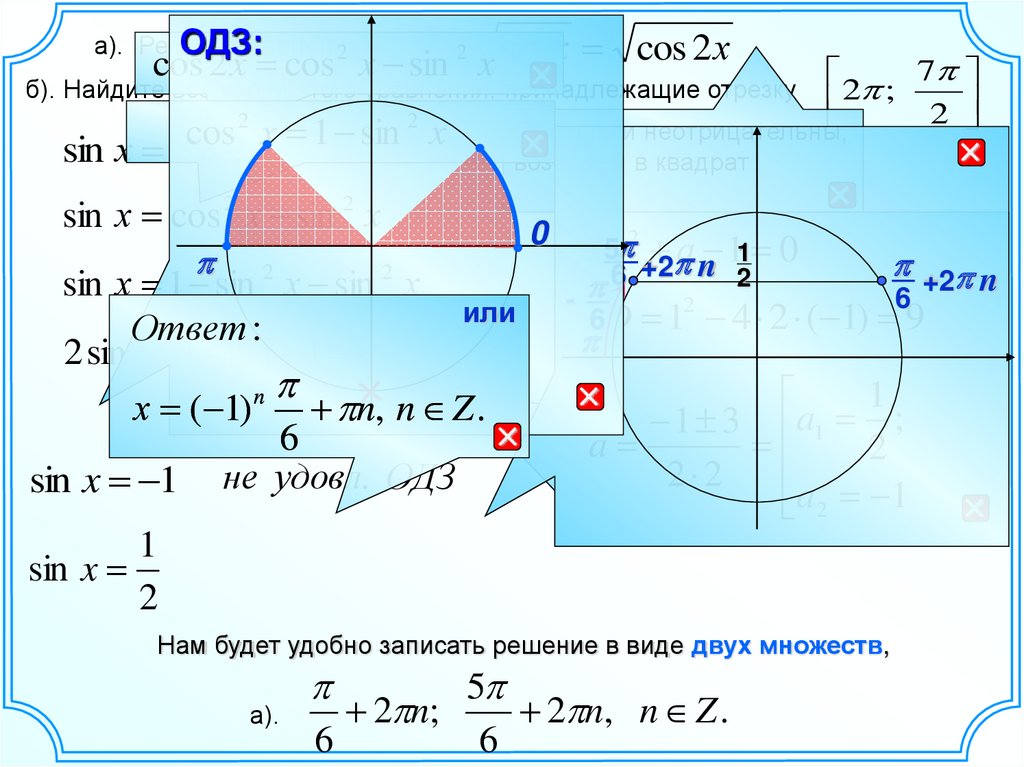
cos 2 x cos x sin 2 x sin х cos 2 хОДЗ:
а). Решите
уравнение
2
7p
2
p
;
2
Обе части неотрицательны,
б). Найдите все корни этого уравнения, принадлежащие отрезку
2
2
cos
x
1
sin
x
sin х cos 2х
возведем в квадрат
sin х cos х sin х
2
p
2
sin х 1 sin х sin х
Ответ
:
2
2 sin х sin х 1 0
2
0
или
p
х ( 1)
pn, n Z .
6
sin x 1 не удовл. ОДЗ
n
25ap2 +2
pa n 11 0
2
-
p6
6D 1
p
2
2
1
1 3 a1 ;
a
2
2 2
a2 1
Нам будет удобно записать решение в виде двух множеств,
а).
p +2p n
6
4 2 ( 1) 9
1
sin x
2
5p
2pn;
2pn, n Z .
6
6
p
3.
Отбор корней с помощью решения неравенствб). Найдите все корни этого уравнения, принадлежащие отрезку
p
n=1
х 2pn
6
7p
2 p;
2
1
7
1
2 2n
6
6
2
11
20
:2
2n
6
6
11
20
n
12
12
13p
n 1, x
6
:p
7p
2p ; 2
5p
х
2pn
6
7p
2
p;
2
5
7
2 2n
6
2
7
16
2n
6
6
n=1
:p
5
6
:2
7
16
n
12
12
n 1,
17p
x
6
4.
б). Найдите все корни этого уравнения, принадлежащие отрезкуОДЗ:
Отбор корней с помощью числовой окружности.
1
sin x
2
17pp
3p –
6
- p
6
7p
2
p
;
2
Найдем этот промежуток
на единичной окружности
5p
2
p
p p+ p
213
6 6
+p
6
1
2
3p
2p
7p
2
0
p
12p p 13p
.
6
6
6
6
6
p 18p p 17p
3p
.
6
6
6
6
6
2p
б).
13p 17p
;
6
6



 mathematics
mathematics