Диэлектрическая проницаемость сред с временной и пространственной дисперсией. (Лекция 3)

1.

Лекция 3. Диэлектрическая проницаемость сред с
временной и пространственной дисперсией
1. Комплексные тензоры проводимости и диэлектрической проницаемости
а. Интегральная формулировка материальных уравнений электродинамики
б. Комплексные проводимость и диэлектрическая проницаемость
2. Соотношения Крамерса-Кронига
а. Два свойства комплексных проводимости и диэлектрической проницаемости
б. Соотношения Крамерса-Кронига для проводимости
в. Соотношения Крамерса-Кронига для диэлектрической проницаемости
г. Применение соотношений Крамерса-Кронига
д. О материальных средах без временной дисперсии
3. Диэлектрическая проницаемость газа осцилляторов
а. Электронная теория диэлектрической проницаемости
б. Нормальная и аномальная дисперсия
4. Диэлектрическая проницаемость изотропной горячей плазмы в
гидродинамическом приближении
а. Уравнения многожидкостной гидродинамики
б. Продольная и поперечная диэлектрические проницаемости изотропной плазмы
5. Диэлектрическая проницаемость плазмы в магнитном поле

2.

j σˆ E , D εˆ E
t
t
ji (t , r )
dt dr ˆ
ij
(t , t , r, r ) E j (t , r ) ,
ji (t , r )
dt dr ˆ
t
t
Di (t , r )
dt dr ˆ
ij
(t , t , r, r ) E j (t , r ) .
Di (t , r )
ij
dt dr ˆ
ij
(t t , r r ) E j (t , r ) ,
(t t , r r ) E j (t , r ) .
E(t , r ) E( , k ) exp( i t ik r )
ji ( , k )
t
dt dr ˆ
ij
(t t , r r ) exp[i (t t ) ik (r r )] E j ( , k )
ji ( , k ) ij ( , k ) E j ( , k )
Di ( , k ) ij ( , k ) E j ( , k )
0
0
ij ( , k ) d dρ ˆ ij ( , ρ) exp(i ik ρ) ij ( , k ) d dρ ˆij ( , ρ) exp(i ik ρ)
ij ( , k ) ij
4 i
ij ( , k )

3.

ˆ ij ( , ρ) ˆ ij ( ) (ρ),
ˆij ( , ρ) ˆij ( ) (ρ) .
0
0
ij ( ) d ˆ ij ( ) exp(i ), ij ( ) d ˆij ( ) exp(i ).
Re ij ( ) Re ij ( ), Im ij ( ) Im ij ( ),
Re ij ( ) Re ij ( ), Im ij ( ) Im ij ( ).
ˆ ij ( ) 0
lim ij ( ) 0 , lim ij ( ) ij
| |
| |
5
ij ( ~ ) ~ ij ( ~ ) ~ ij ( ~ ) ~
ij ( ~ ) ~
ij ( ~ ) ~
d
d
d
d
~
~
~
~
~ d 0
С
С
4
( ~ ) ~
1
ij ( )
V.p. ~ij
d
i
Im ij ( ~ ) ~
1
Re ij ( ) V.p. ~
d ,
Re ij ( ~ ) ~
1
Im ij ( ) V.p. ~
d .
ij ( ~ )
~
3
2
1
4
2
2
4

4.

ij ( ~ ) ij ~ 4 ij (0)
1
ij ( ) ij
V.p.
d i
~
i
Im ij ( ~ ) ~
1
Re ij ( ) ij V.p. ~
d ,
Re ij ( ~ ) ij ~ 4 ij (0)
1
Im ij ( ) V.p.
d
.
~
ij ( ) ( 0 i 0 ) ij , ij (0) 0
02
Re ( )
4 2 2
02 1
( ) i
,
4 i
02
( ) 1
( i )
2
1
1
0
~
Im ( )
V.p. ~
d
2
2
2
2
~
4
4
(
)(
)
2
0
0
(
)
ˆ ij ( ) ( ) ij
ij
0
ij
ij ( ) ij
4 i 0
ij ˆij ( ) ij ( ) 4 ij0

5.

ji ( , k ) ij ( , k ) E j ( , k )
ij ( , k ) ij
Di ( , k ) ij ( , k ) E j ( , k )
4 i
ij ( , k )
d s2d e Re{E( , k ) exp[ i t ik (r d)]}
d
m
P (t , r ) еn0d(t , r )
e 2 n0
1
P (t , r ) P( , k ) exp( i t ik r ), P ( , k )
E( , k )
2
2
m s i
02
2
4
e
n0 m
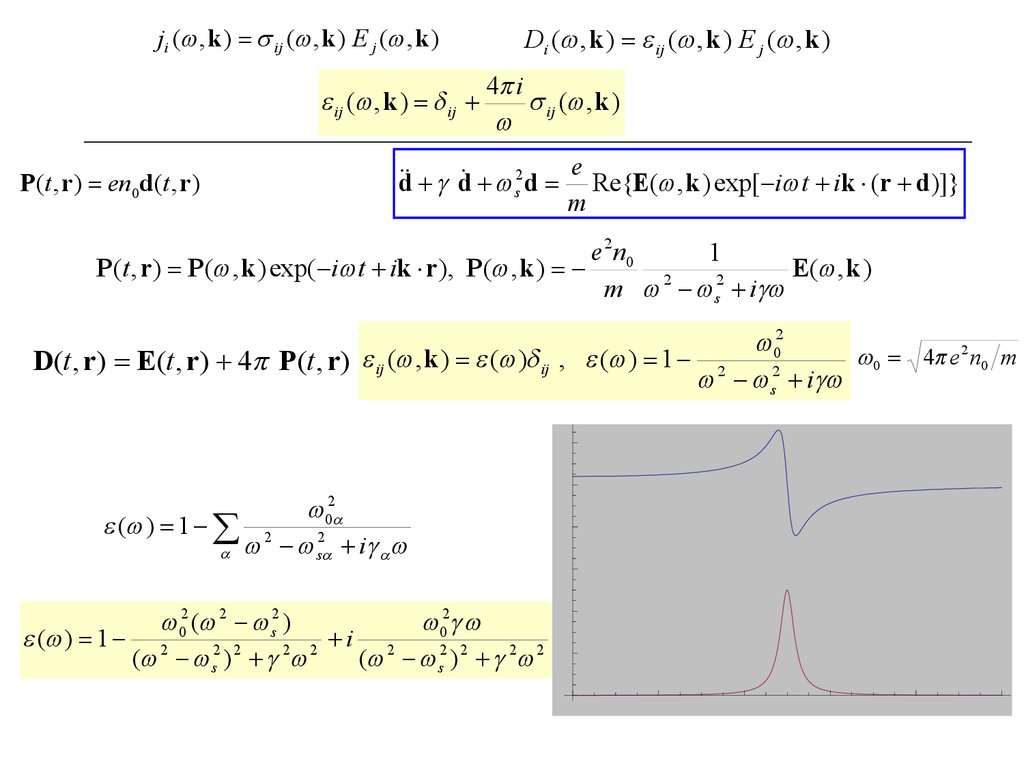
D(t , r ) E(t , r ) 4 P(t , r ) ij ( , k ) ( ) ij , ( ) 1 2
0
2
s i
1 .2
( ) 1
2 s2 i
2
0
02 ( 2 s2 )
02
( ) 1 2
i 2
2 2
2 2
( s )
( s2 ) 2 2 2
1 .0
0 .8
0 .6
0 .4
0 .2
2
4
6
8
10

6.

N
N V 0,
t
V
N e
1
V V V 2
E
V
B
V .
t
N
m
c
j e N V ,
e N ,
2 j
L2 E
j
2
V
(
j
)
t 2
4 t
t
l
tr
k 2V 2
L2
E
j ( , k ) i
E 1
2 2
4 [ ( i ) k V ]
( i )
L2
( , k ) 1
2 2
( i ) k V
l
L2
( , k ) 1
2 2
( i ) k V
tr
k 2V 2
1
( i )
D( , k ) l ( , k )E l ( , k ) tr ( , k )E tr ( , k )
2
L
l ( , k ) tr ( , k ) ( ) 1
( i )

7.

ki k j
k (k E)
l
E
Ei 2 E j ,
2
k
k
l
ki k j
E E E E ij 2 E j ,
k
tr
l
tr
i
l
ki k j
ki k j
tr
Di ( , k ) ( , k ) 2 ( , k ) ij 2
k
k
ij ( , k )
ki k j
k2
ki k j
( , k ) ij 2
k
l
E j ( , k )
tr
( , k )
V
e
V b 0
E V
t
m
j e N 0 V
L2
i ( i ) j ( , k ) j ( , k ) b 0
E( , k )
4

8.

(4 ) 1 L2
j x i
[( i ) E x i E y ] ,
2
2
( i )
(4 ) 1 L2
j y i
[( i ) E y i E x ] ,
( i ) 2 2
(4 ) 1 L2
j z i
Ez .
( i )
ji ( , k ) ij ( , k ) E j ( , k ) , i, j x, y, z
0
xx ( ) xy ( )
ij ( , k ) ij ( ) yx ( ) yy ( )
0 ,
0
0
zz ( )
xx ( ) yy ( ) (4 ) 1 i
( i )
,
2
2
( i )
2
L
L2 ( i )
xx ( ) yy ( ) 1
,
2
2
[( i ) ]
2
L
1
(
)
(
)
i
,
xy ( ) yx ( ) (4 )
,
xy
yx
2
2
2
2
[( i ) ]
( i )
L2
L2
1
zz ( ) 1
,
zz ( ) (4 ) i
.
(
i
)
i
xz yz zx zy 0 .
2
L