Engineering Mechanics Part II: Dynamics. Lectures 1 - 3

1. Engineering Mechanics Part II: Dynamics Dr. Bahaa Saleh

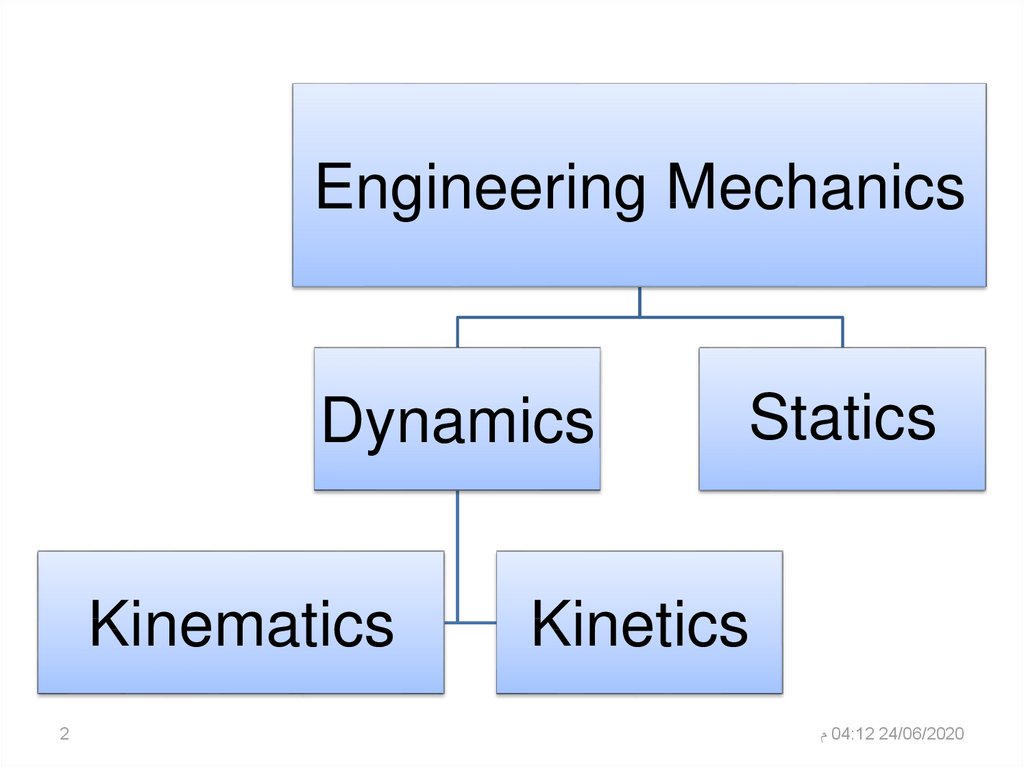
2.

Engineering Mechanics
Dynamics
Kinematics
2
Statics
Kinetics
‫ م‬04:12 24/06/2020

3.

Course Supplemental Materials
Textbook - Engineering Mechanics:
Dynamics, R. C. Hibbeler, 8th Edition,
Pearson Prentice Hall, 1998.
References: Engineering Mechanics:
Dynamics , J . L. Meriam and L. G. Kraige ,
6th Edition, John Wiley & Sons, Inc., 2008.
Lectures Notes prepared by instructors.

4. Course Grading System

• 20%
• 20%
• 20%
• 40%
Attendance, participation,
Quizzes and assignments
1st Midterm Exam
2nd Midterm Exam
Final Exam

5. Course Topics

• Chapter 1: Introduction to dynamics
• Chapter 2: Kinematics of a Particle:
Topic # 1: Particle motion along a straight line
Topic # 2: Particle motion along a curved path
Topic # 3: Dependent motion of connected particles
Topic # 4: Relative motion of two particles
• Chapter 3: Kinetics of a Particle:
Topic # 1: Force and Acceleration
Topic # 2: Work and energy
Topic # 3: Impulse and momentum

6. Course Topics – Cont.

• Chapter 4: Planer Kinematics of a Rigid
Body.
• Chapter 5: Planar Kinetics of a Rigid
Body: Force and Acceleration.
• Chapter 6: Introduction to Mechanical
Vibration.
6
‫ م‬04:12 24/06/2020

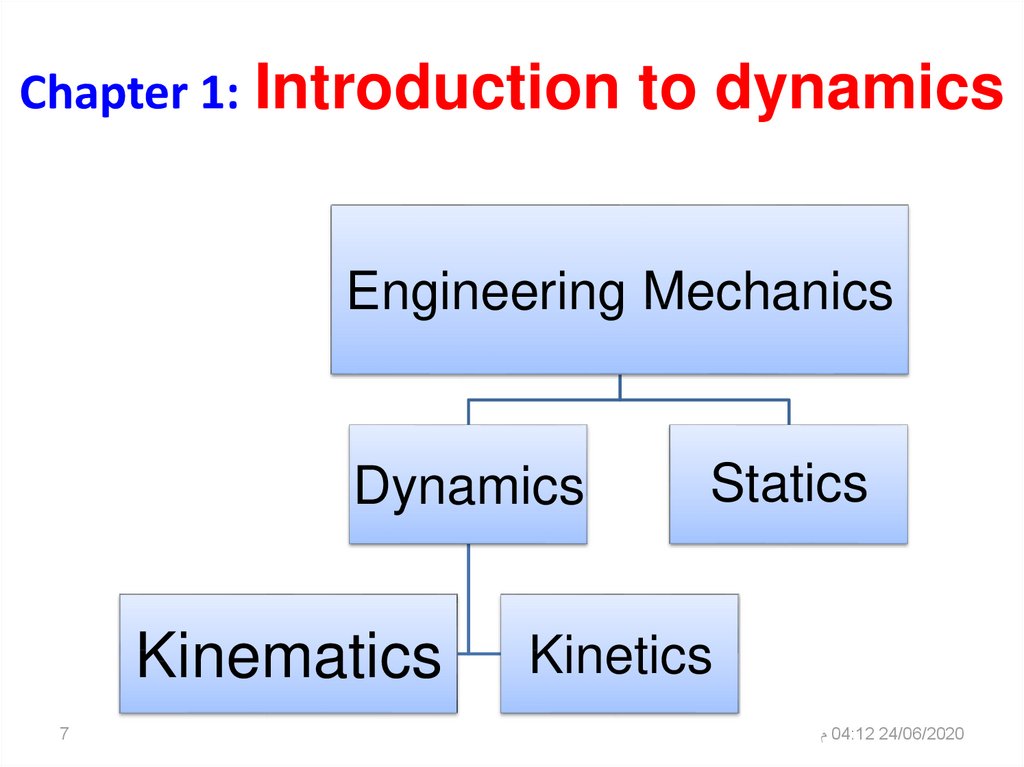
7. Chapter 1: Introduction to dynamics

Engineering Mechanics
Dynamics
Kinematics
7
Statics
Kinetics
‫ م‬04:12 24/06/2020

8. Definitions

• Statics: concerned with the
equilibrium of a body that is
either at rest or moves with
constant velocity.
8
‫ م‬04:12 24/06/2020

9. Definitions – Cont.

Dynamics
1- Kinematics: study of the motion of
particles/rigid
bodies
(relate
displacement, velocity, acceleration,
and time, without reference to the
cause of the motion).
• 2- Kinetics: study of the forces acting
on the particles/rigid bodies and the
motions resulting from these forces.
9
‫ م‬04:12 24/06/2020

10. Definitions – Cont.

• Rigid Body
• Particle
10
‫ م‬04:12 24/06/2020

11. Review of Vectors and Scalars

• A Scalar quantity has magnitude only.
• A Vector quantity has both magnitude and
direction.

12.

• Scalars (e.g)
– Distance
– Mass
– Temperature
– Pure numbers
– Time
– Pressure
– Area
– Volume
• Vectors (e.g.)
– Displacement
– Velocity
– Acceleration
– Force

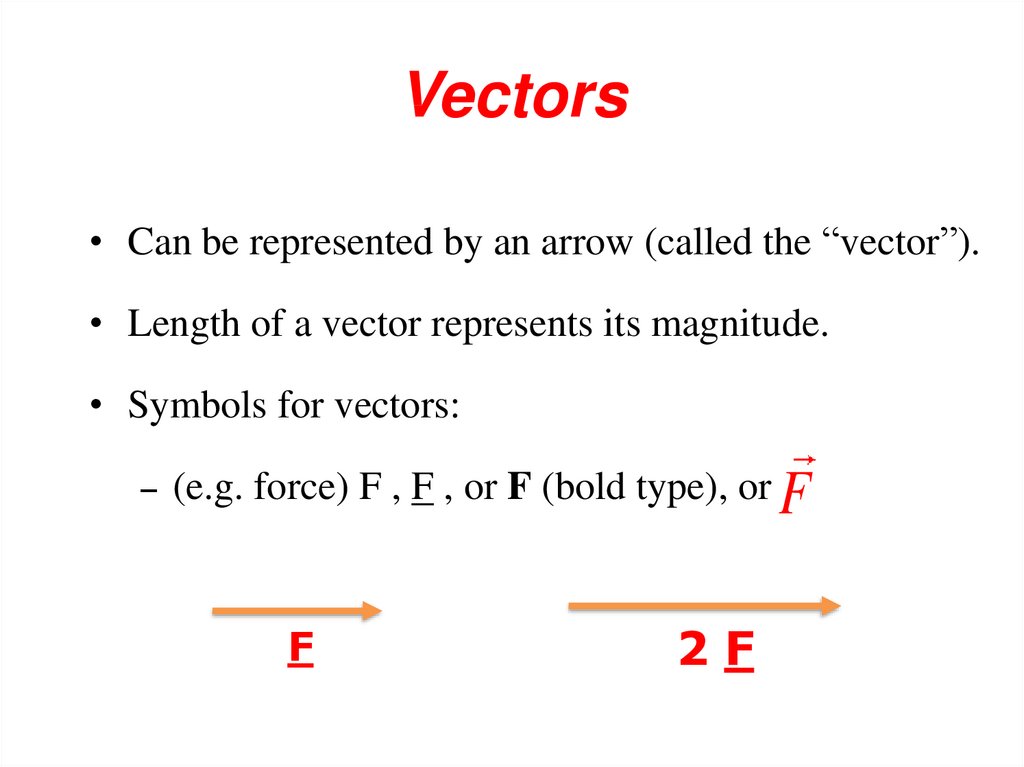
13. Vectors

• Can be represented by an arrow (called the “vector”).
• Length of a vector represents its magnitude.
• Symbols for vectors:
–
(e.g. force) F , F , or F (bold type), or F
F
2F

14. Chapter 2: Kinematics of a Particle: Topic # 1: Particle motion along a straight line (Rectilinear Motion)

15. Definition

Rectilinear motion: A particle moving
along a horizontal/vertical/inclined straight
line.

16. Position of the particle (horizontal)

• Since the particle is moving, so the
position is changing with time (t):
• OP = Position = S = S (t)

17. Displacement of the particle (horizontal)

• Displacement (∆s) : The displacement
of the particle is the change in its
position.

18. Displacement of the particle (horizontal)

1- ∆S is positive since the particle's final
position is to the right of its initial position,
i.e., s` > s.
2- If the final position to the left of its initial
position, ∆S would be negative.

19. Velocity of the particle (horizontal)

• Velocity (v) : If the particle displacement ∆s during
time interval ∆t, the average velocity of the
particle during this time interval is (displacement
per unit time)
• The magnitude of the velocity is known as the
speed, and it is generally expressed in units of m/s
v av
s
t

20. Velocity of the particle (horizontal)

• Instantaneous velocity :
s
V lim
t 0 t
ds
v
dt
• So (v) is a function of time (t):
v v(t)

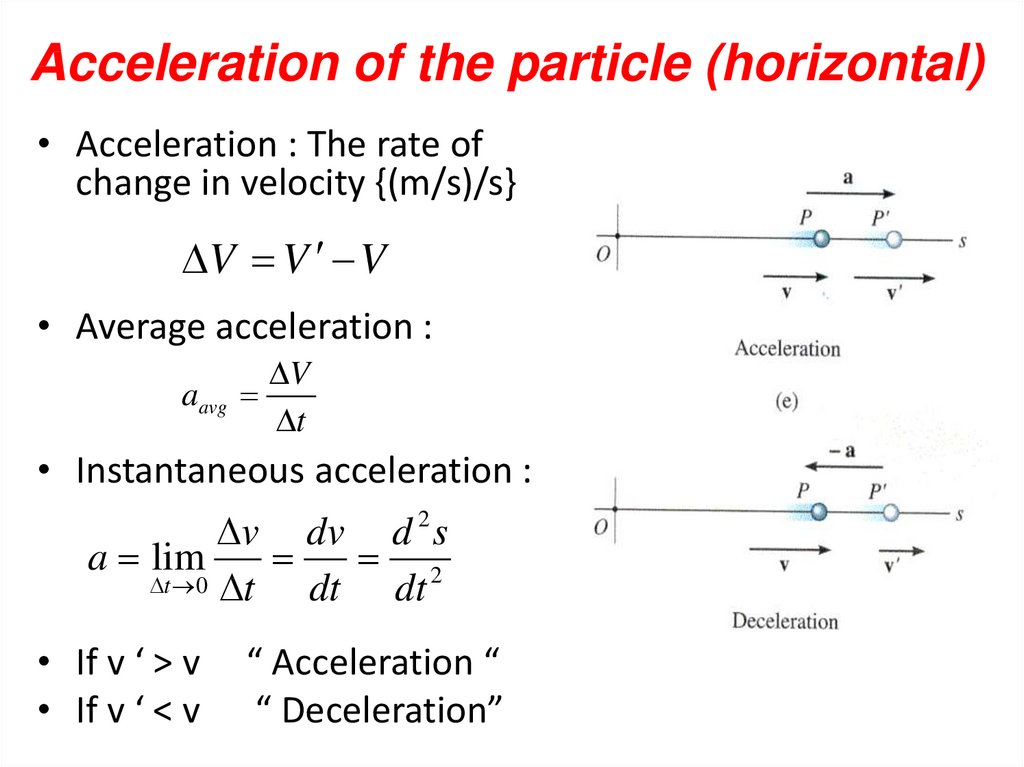
21. Acceleration of the particle (horizontal)

• Acceleration : The rate of
change in velocity {(m/s)/s}
V V V
• Average acceleration :
aavg
V
t
• Instantaneous acceleration :
v dv d 2 s
a lim
2
t 0 t
dt dt
• If v ‘ > v
• If v ‘ < v
“ Acceleration “
“ Deceleration”

22. Acceleration of the particle (horizontal)

• Acceleration (a) : is the rate of change of
velocity with respect to time.
2
dv d s
a
2
dt dt

23. Solved Examples

Example 1
• A particle moves along a straight line such that its
position is defined by s = (t3 – 3 t2 + 2 ) m.
Determine the velocity of the particle when t = 4 s.
ds
2
v
3t 6t
dt
At t = 4 s,
the velocity (v) = 3 (4)(4) – 6(4) = 24 m/s

24.

Example 2
• A particle moves along a straight line such that its
position is defined by s = (t3 – 3 t2 + 2 ) m.
Determine the acceleration of the particle when
t = 4 s.
ds
v
3t 2 6t
dt
dv
a
6t 6
dt
• At t = 4
a(4) = 6(4) - 6 = 18 m/s2

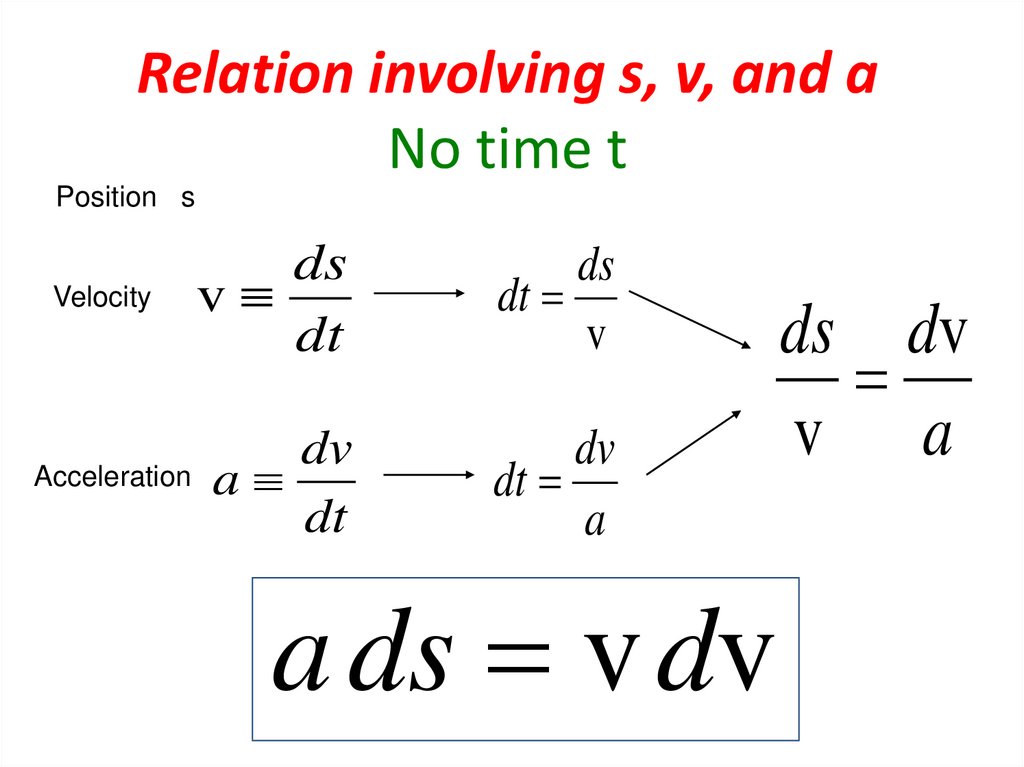
25. Relation involving s, v, and a No time t

Position s
Velocity
Acceleration
ds
v
dt
ds
dt
v
dv
a
dt
dv
dt
a
a ds v dv
ds dv
v a

26. Motion with uniform/constant acceleration a

dv
a
dt
v
t
vo
0
dv
a
dt
dv a dt
v v 0 at
v v 0 at

27. Motion with uniform/constant acceleration a

ds
v
v0 a t
dt
s
t
so
0
ds
(
v
a
t
)
dt
0
1 2
s s0 v 0 t a t
2

28. Motion with uniform/constant acceleration a

v dv a ds
v
s
v0
s0
v
d
v
a
ds
1 2 1 2
v v 0 ac ( s s 0 )
2
2
v v 2 a ( s s0 )
2
2
0

29. Summary

• Time dependent acceleration
• Constant acceleration
s s (t )
v v0 a t
ds
v
dt
2
dv d s
a
2
dt dt
a ds v dv
1 2
s s0 v 0 t a t
2
v v 2 a ( s s0 )
2
2
0

30.

Example 3
• A car moves in a straight line such that for a short time its
velocity is defined by v = (3t^2 + 2t) m/s, where t is in
seconds. Determine its position and acceleration when t =
3 s. (When t = 0, s = o).
When t = 3 s
s 3 3 36 m
3
2
a 6 * 3 2 20 m s
2

31. Chapter 2: Kinematics of a Particle: Topic # 2: Particle Motion along a Curved Path

32.

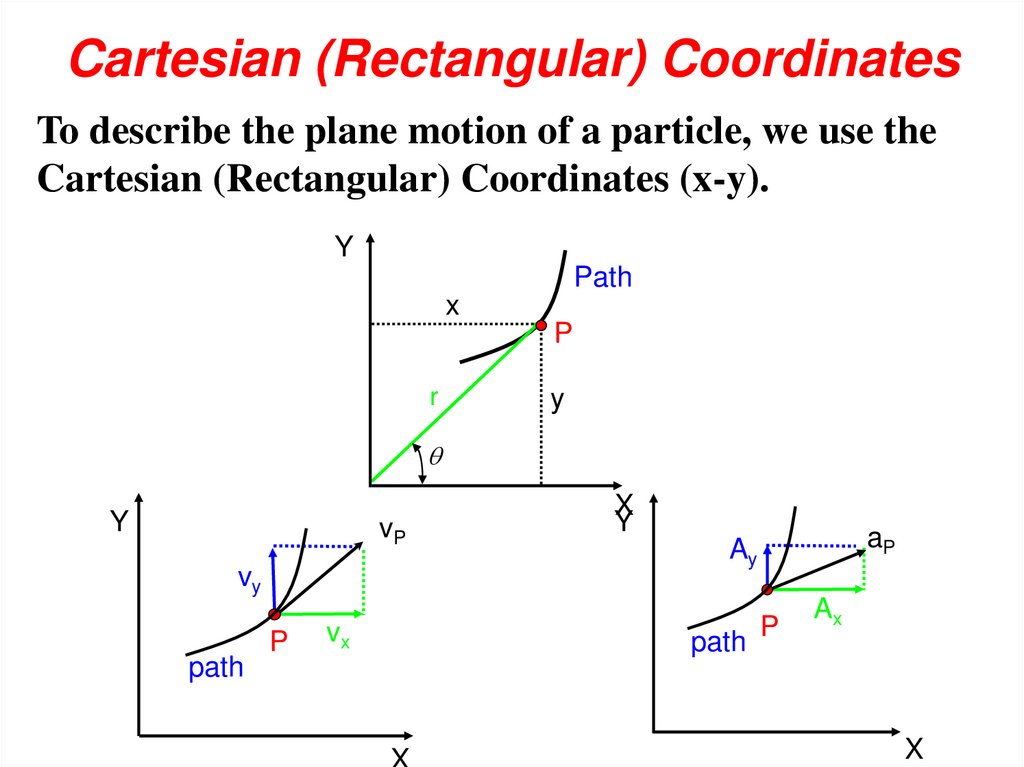
Cartesian (Rectangular) Coordinates
To describe the plane motion of a particle, we use the
Cartesian (Rectangular) Coordinates (x-y).
Y
Path
x
P
r
y
Y
vP
vy
path
P
vx
X
Y
path
X
aP
Ay
P
Ax
X

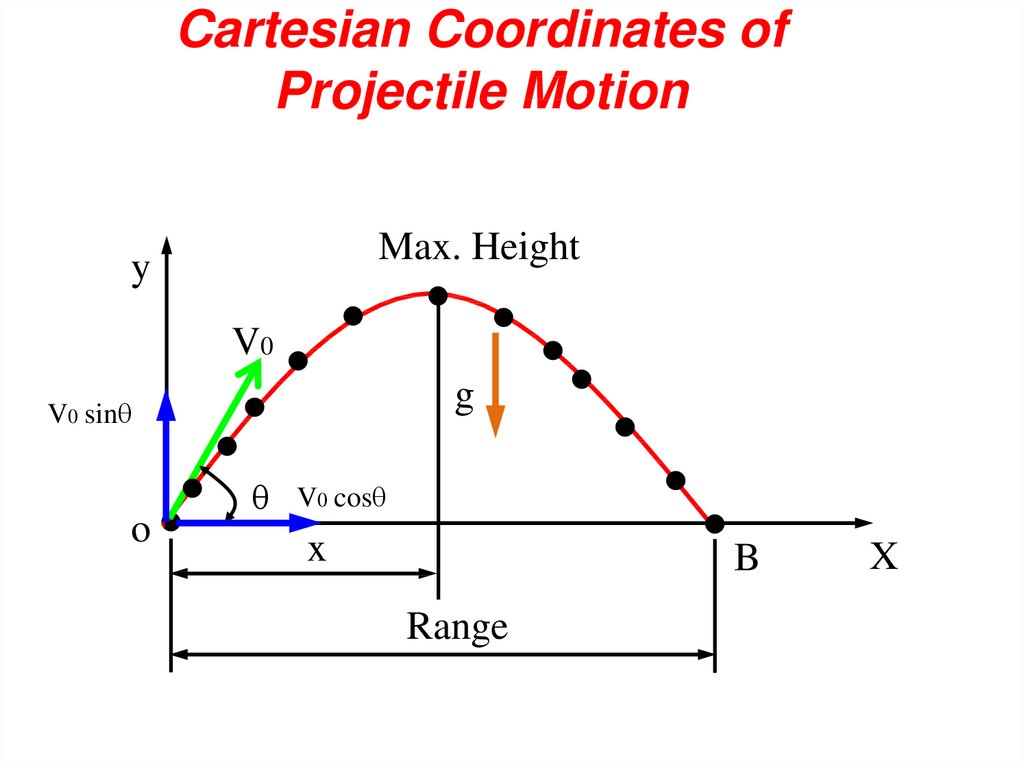
33. 12Projectile Motion

• Projectile: any body that is given an initial
velocity and then follows a path determined by
the effects of gravitational acceleration and air
resistance.
• Trajectory – path followed by a projectile

34.

Cartesian Coordinates of
Projectile Motion
Max. Height
y
V0
g
V0 sin
o
V0 cos
x
B
Range
X

35.

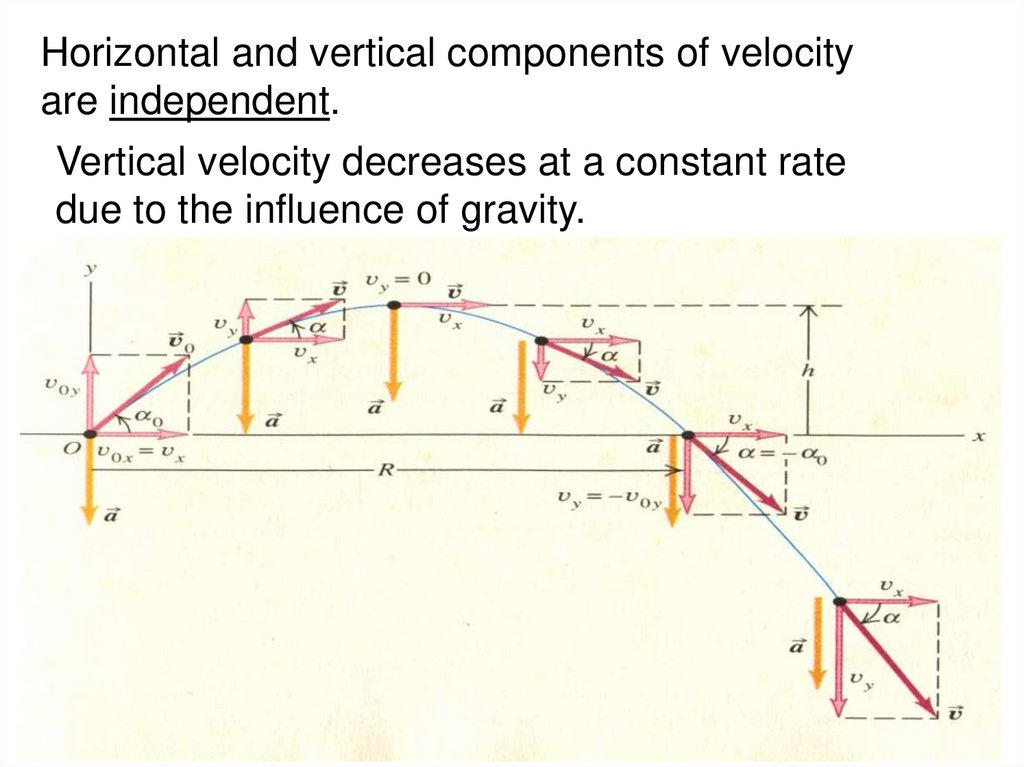
Horizontal and vertical components of velocity
are independent.
Vertical velocity decreases at a constant rate
due to the influence of gravity.

36.

Cartesian Coordinates of
Projectile Motion
• Assumptions:
(1) free-fall acceleration
(2) neglect air resistance
• Choosing the y direction as positive upward:
ax = 0;
ay = - g (a constant)
y
v0
• Take x0= y0 = 0 at t = 0
• Initial velocity v0 makes an
x
angle with the horizontal
v 0x v 0 cosθ
v 0y v 0sin θ

37. Horizontal Motion of Projectile

• Acceleration in X-direction: ax= 0
• Integrate the acceleration yields:
( ) v x v 0 cosθ constant
• Integrate the velocity yields:
( ) x v 0 t cosθ

38. Vertical Motion of Projectile

• ay = ac= -g = -9.81 m/s2
• Integrate the acceleration yields:
( ) v v0 ac t
( )
v y (v0 ) y gt
v y v 0 sinθ gt
• Integrate the velocity yields:
( )
gt 2
y v 0 t sinθ
2

39.

• ax = 0;
ay = - g (a constant)
• Integration of these acceleration yields
v x v0 cosθ constant
v y v 0 sin θ g t
x v 0 t cosθ
(1)
y v 0 t sin θ g t /2
2
(2)
• Elimination of time t from Eqs. 1 & 2 yields
• Equation of the path of projectile
y x tan θ (g x sec θ / 2 v )
2
2
2
o
(3)

40.

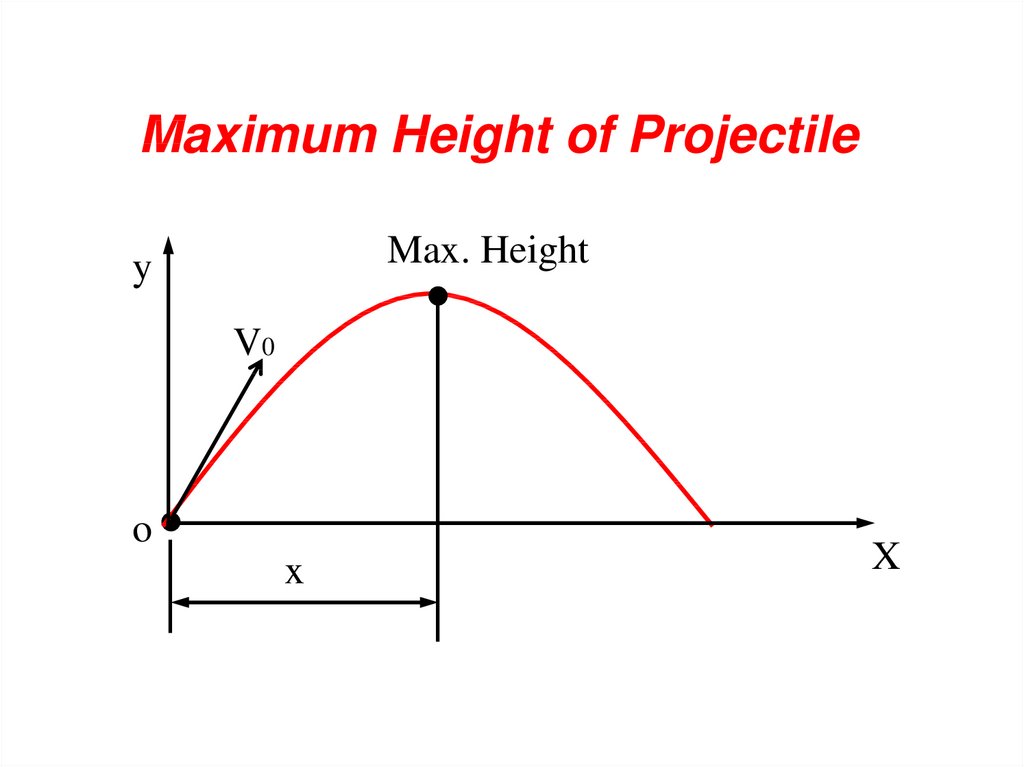
Maximum Height of Projectile
Max. Height
y
V0
o
x
X

41.

Maximum Height of Projectile
At the peak of its trajectory, vy = 0.
v y v 0y a t v o sin gt 0
v 0 sin
Time t1 to reach the peak t1
g
g
1 2
Substituting into: y v 0 sin t gt
2
v 0y
h y max
v 0sinθ 1 v 0 sinθ
g
v 0sinθ
g 2 g
v 0sinθ
2
h y max
g
1 v 0sinθ
2
g
2
2

42.

Maximum Height of Projectile
v 0 sin
1 v 0 sin
2
g
2
h y max
h y max
2
g
(v o sin )
v sin v
2g
2g
2g
2
2
o
2
2
0y
v 0 sinθ
v 0 sinθ
x v 0x t v 0x
v 0 cosθ
g
g
2
v o sin 2θ
sin2θ
x
sinθ cosθ
2g
2

43.

Maximum Height of Projectile and
the corresponding time and X
h y max
v sin
2g
2
o
2
o
v sin 2θ
x
2g
v 0 sin
t1
g
2

44.

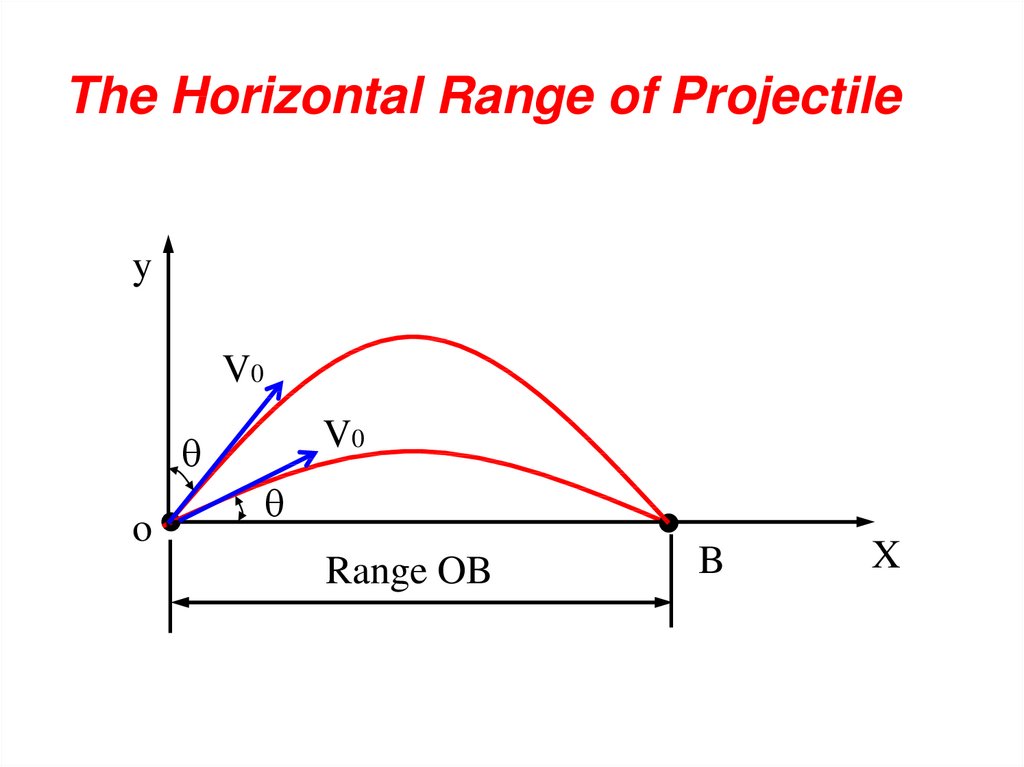
The Horizontal Range of Projectile
y
V0
V0
o
Range OB
B
X

45.

The Horizontal Range of Projectile
The range (OB) where y = 0.
1 2
y v 0 sin t gt
2
Time for the range OB
2 v 0 sin
tB
g
For the rang OB substitute into:
x v 0 t B cosθ
2
o
2v o
v
X OB v o cosθ
sinθ
2 sinθ cosθ
g
g
2
2
vo
vo
X OB
sin2(90 - θ)
sin2 θ
g
g

46.

The Horizontal Range of Projectile
From the Rang equation it is clear that an
angle of firing with the horizontal gives the
same range OB as an angle of firing (90 - )
with the horizontal or as an angle of with
vertical.

47.

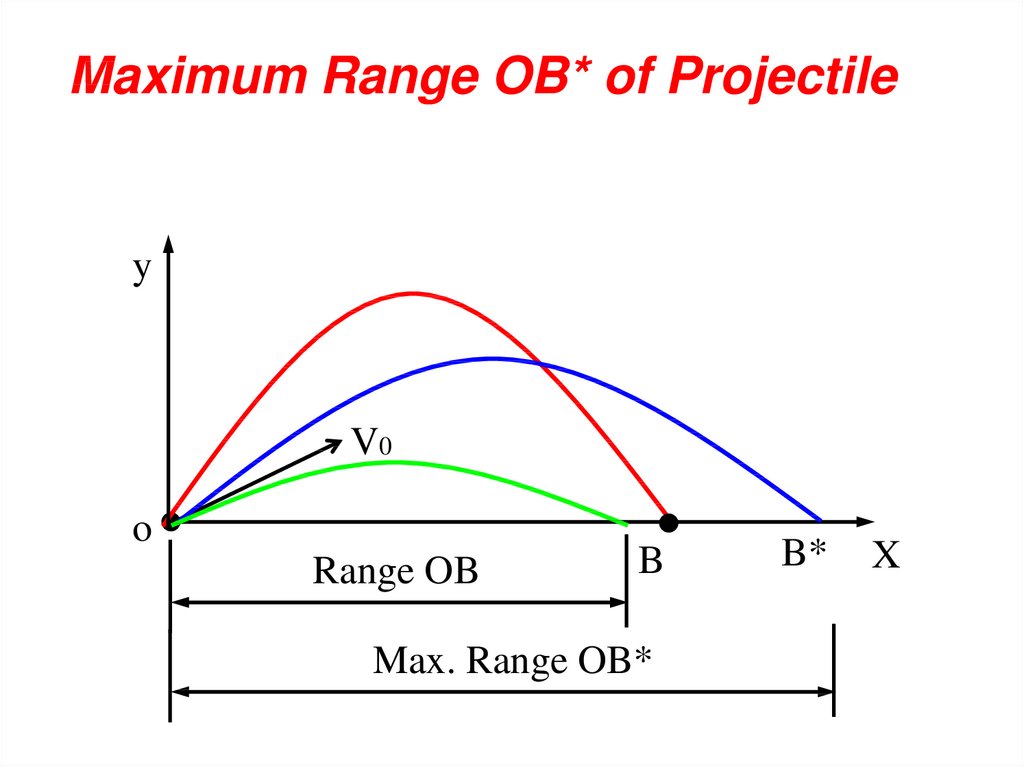
Maximum Range OB* of Projectile
y
V0
o
Range OB
B
Max. Range OB*
B*
X

48.

Maximum Range OB* of Projectile
To calculate max. Range (OB*) and its angle
2
o
v
X OB
sin2(90 - θ)
g
sin2(90 - θ) 1 sin(2 )
θ 45
2
vo
OB
g
*
o

49.

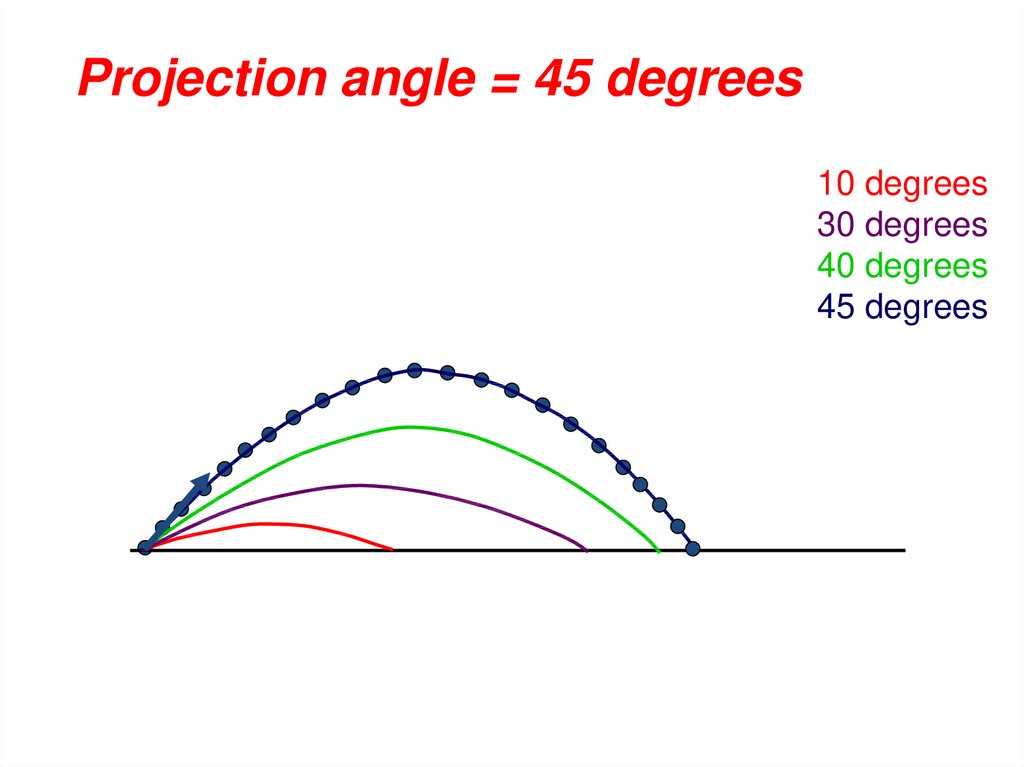
Projection Angle
• The optimal angle of projection is dependent
on the goal of the activity.
• For maximal height the optimal angle is 90o.
• For maximal horizontal distance the optimal
angle is 45o.

50.

Projection angle = 10 degrees
10 degrees

51.

Projection angle = 45 degrees
10 degrees
30 degrees
40 degrees
45 degrees

52.

Projection angle = 60 degrees
10 degrees
30 degrees
40 degrees
45 degrees
60 degrees
80 degrees

53.

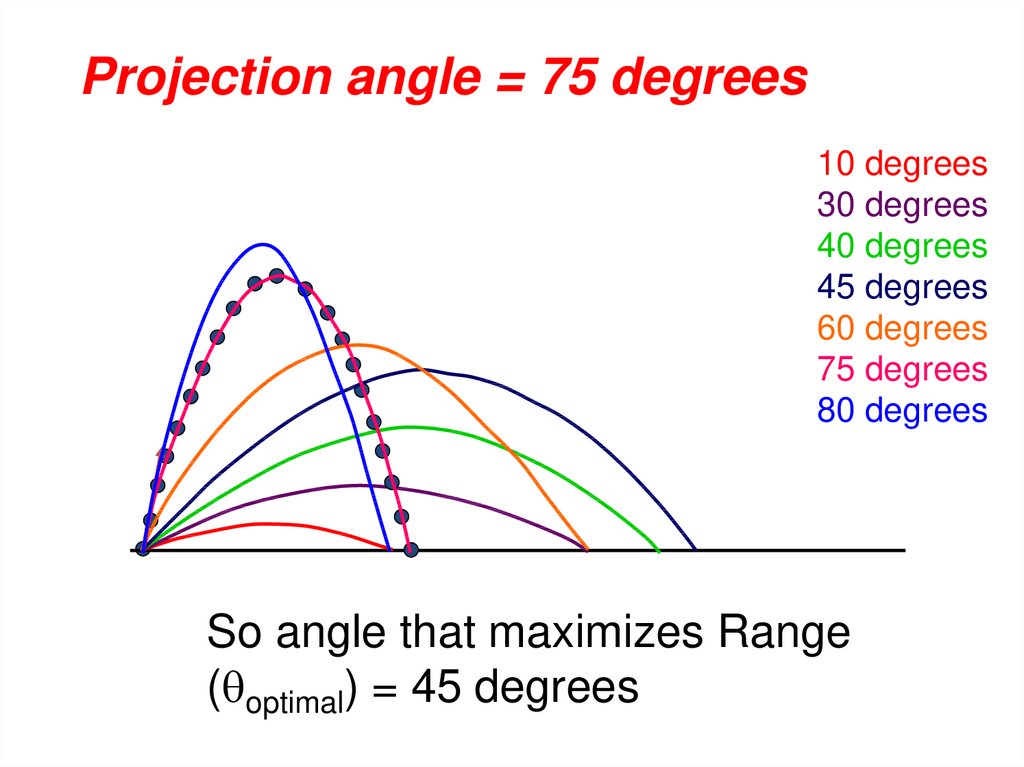
Projection angle = 75 degrees
10 degrees
30 degrees
40 degrees
45 degrees
60 degrees
75 degrees
80 degrees
So angle that maximizes Range
( optimal) = 45 degrees

54.

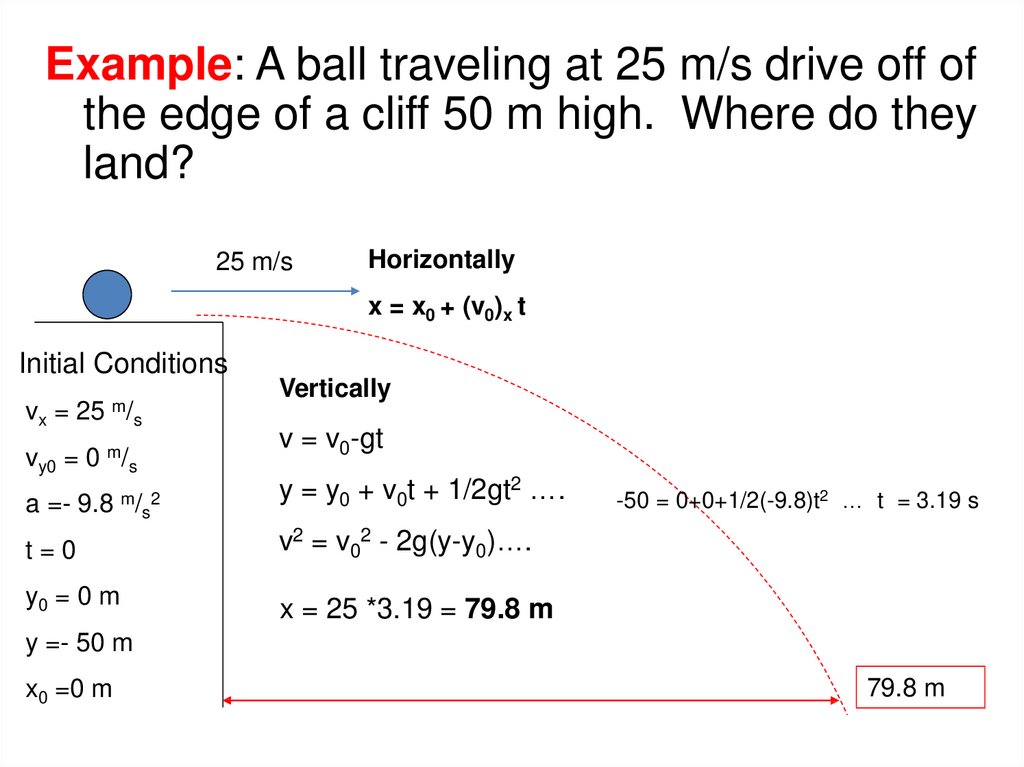
Example: A ball traveling at 25 m/s drive off of
the edge of a cliff 50 m high. Where do they
land?
25 m/s
Horizontally
x = x0 + (v0)x t
Initial Conditions
vx = 25
m/
s
vy0 = 0 m/s
a =- 9.8
m/ 2
s
Vertically
v = v0-gt
y = y0 + v0t + 1/2gt2 ….
t=0
v2 = v02 - 2g(y-y0)….
y0 = 0 m
x = 25 *3.19 = 79.8 m
-50 = 0+0+1/2(-9.8)t2 … t = 3.19 s
y =- 50 m
x0 =0 m
79.8 m