Построение сечений тетраэдра

1.

.

2.

D
M
N
K
L
C
A
B
P
E
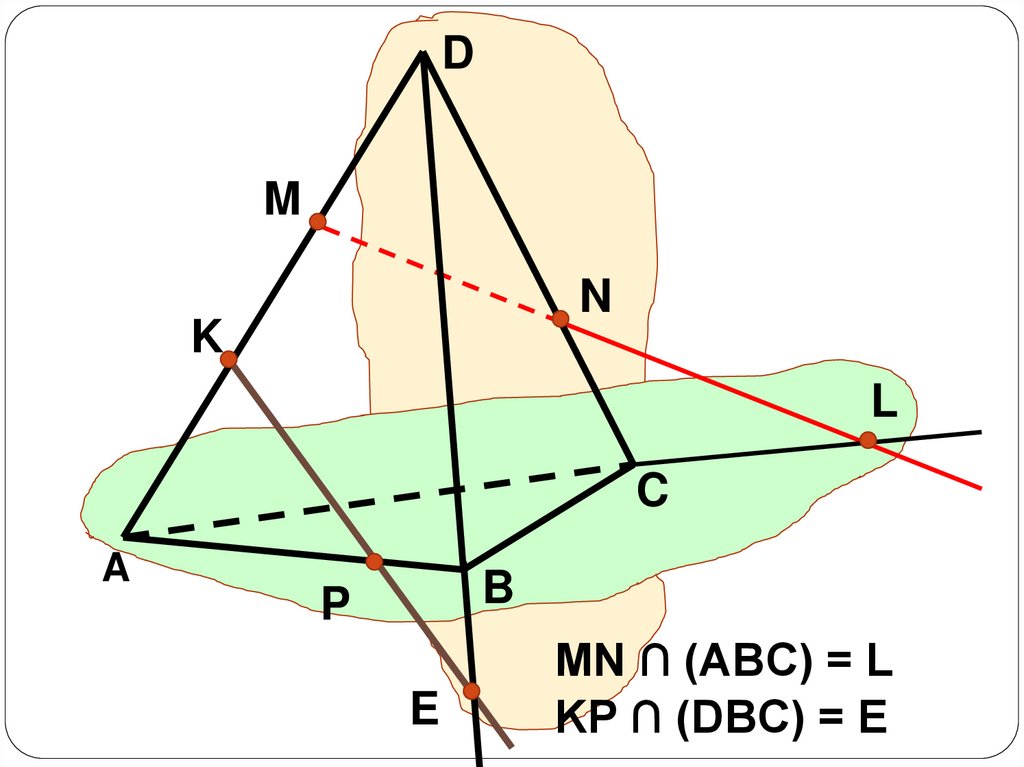
MN ∩ (ABC) = L
KP ∩ (DBC) = E

3.

M
M
P
D
H
N
K
X
К
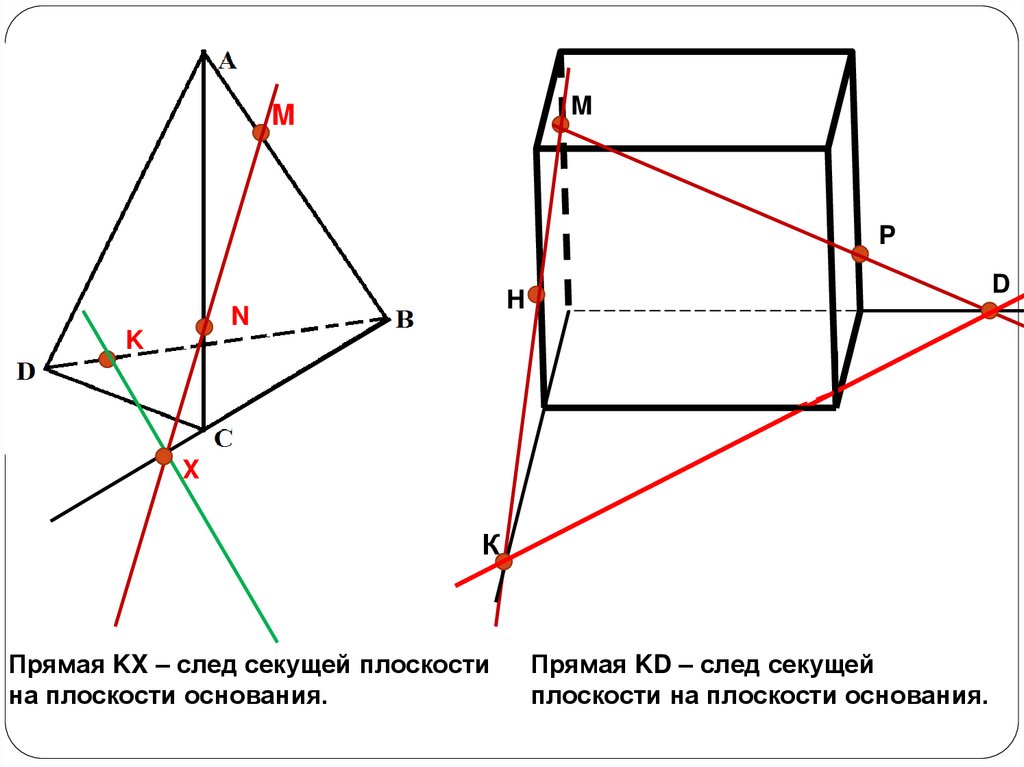
Прямая KX – след секущей плоскости
на плоскости основания.
Прямая KD – след секущей
плоскости на плоскости основания.

4.

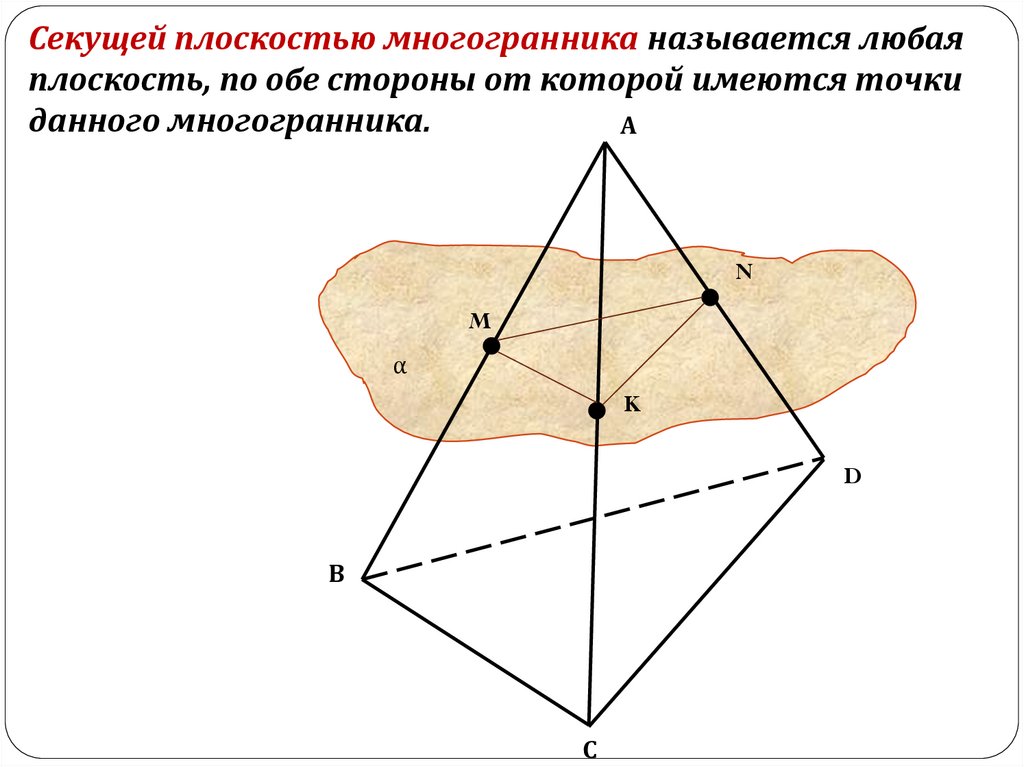
Секущей плоскостью многогранника называется любая
плоскость, по обе стороны от которой имеются точки
данного многогранника.
А
N
M
α
K
D
В
С

5.

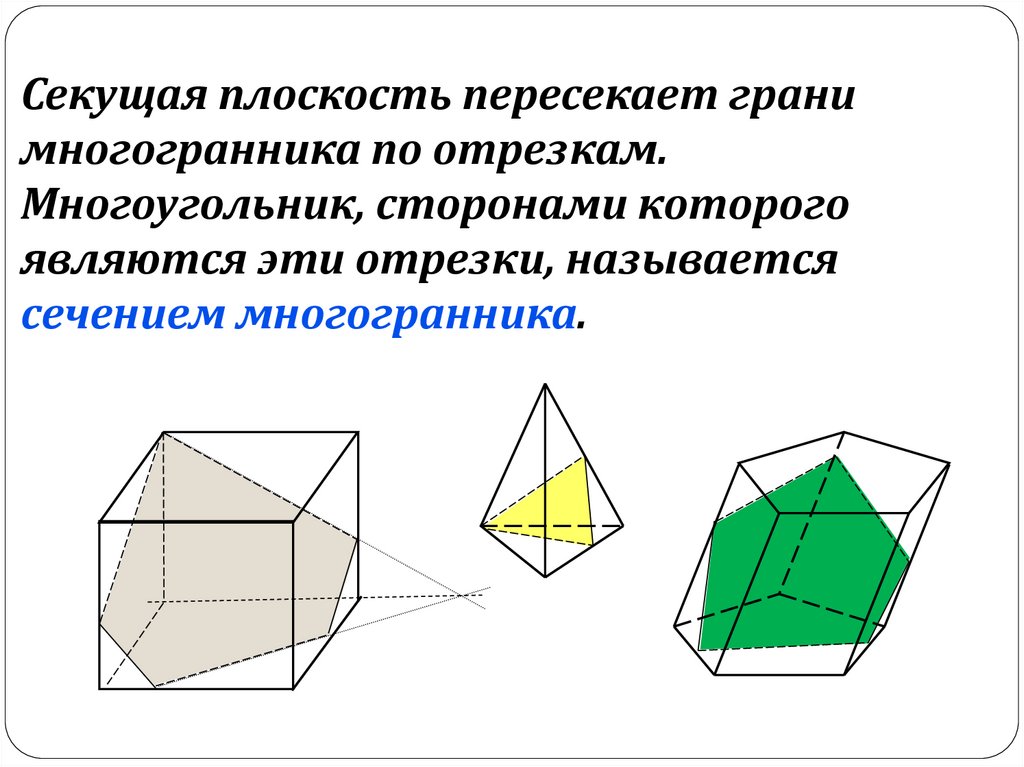
Секущая плоскость пересекает грани
многогранника по отрезкам.
Многоугольник, сторонами которого
являются эти отрезки, называется
сечением многогранника.

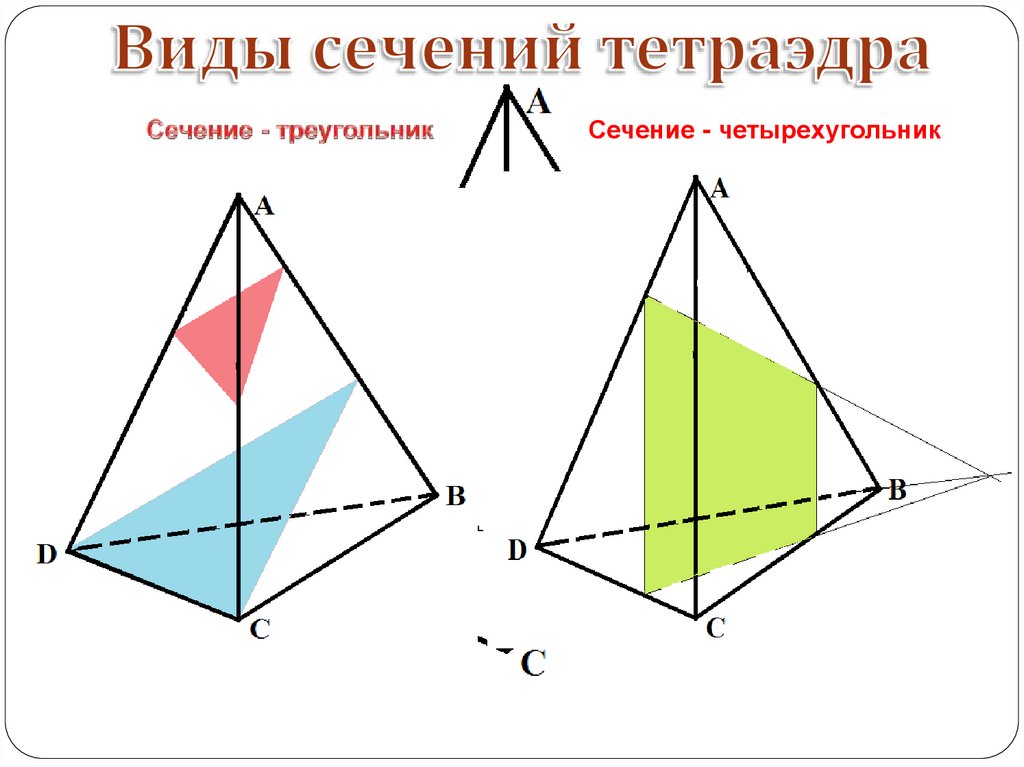
6.

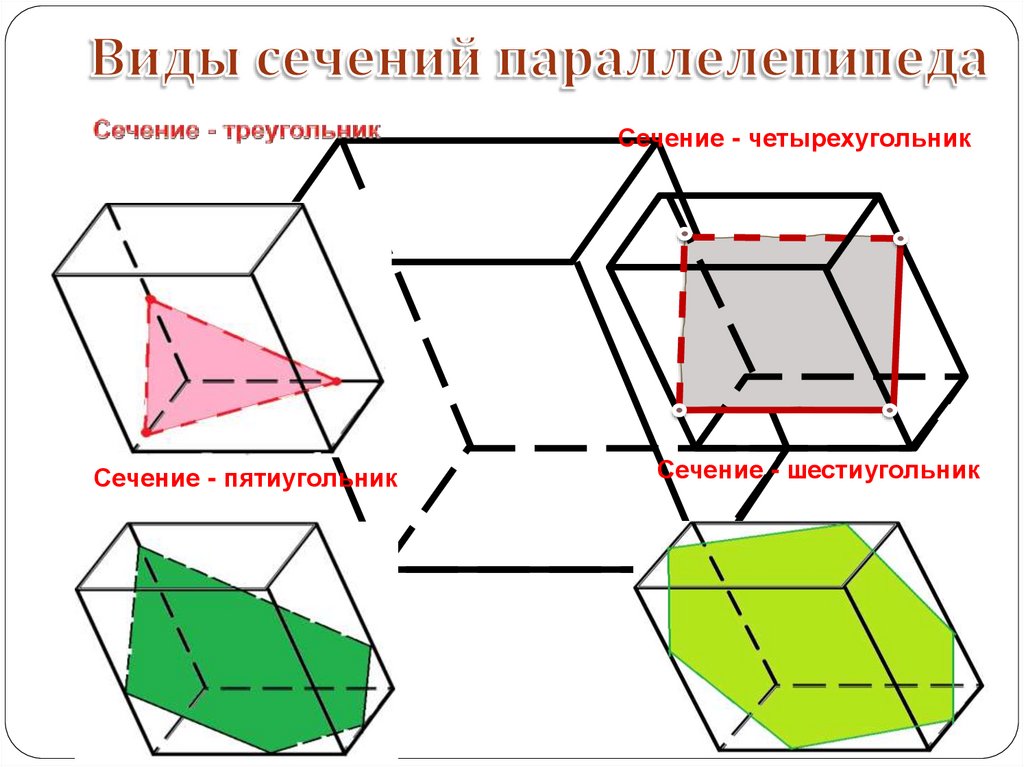
Сечение - четырехугольник

7.

Сечение - четырехугольник
Сечение - пятиугольник
Сечение - шестиугольник

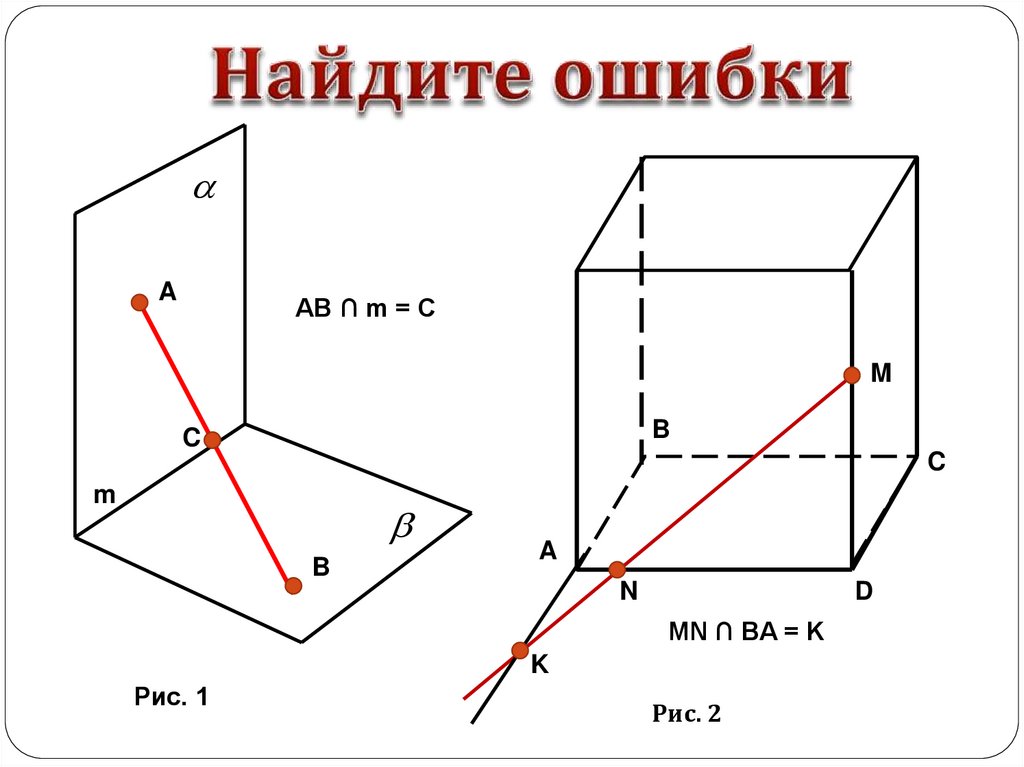
8.

A
AB ∩ m = C
M
B
C
C
m
B
A
N
D
MN ∩ BA = K
K
Рис. 1
Рис. 2

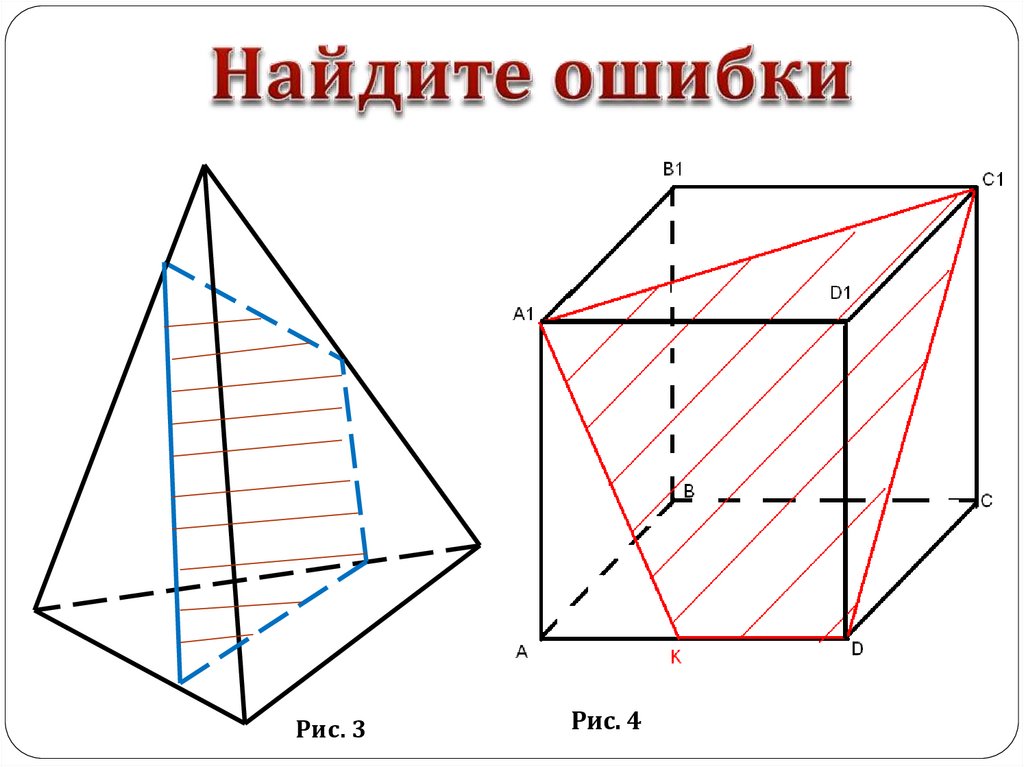
9.

Рис. 3
Рис. 4

10.

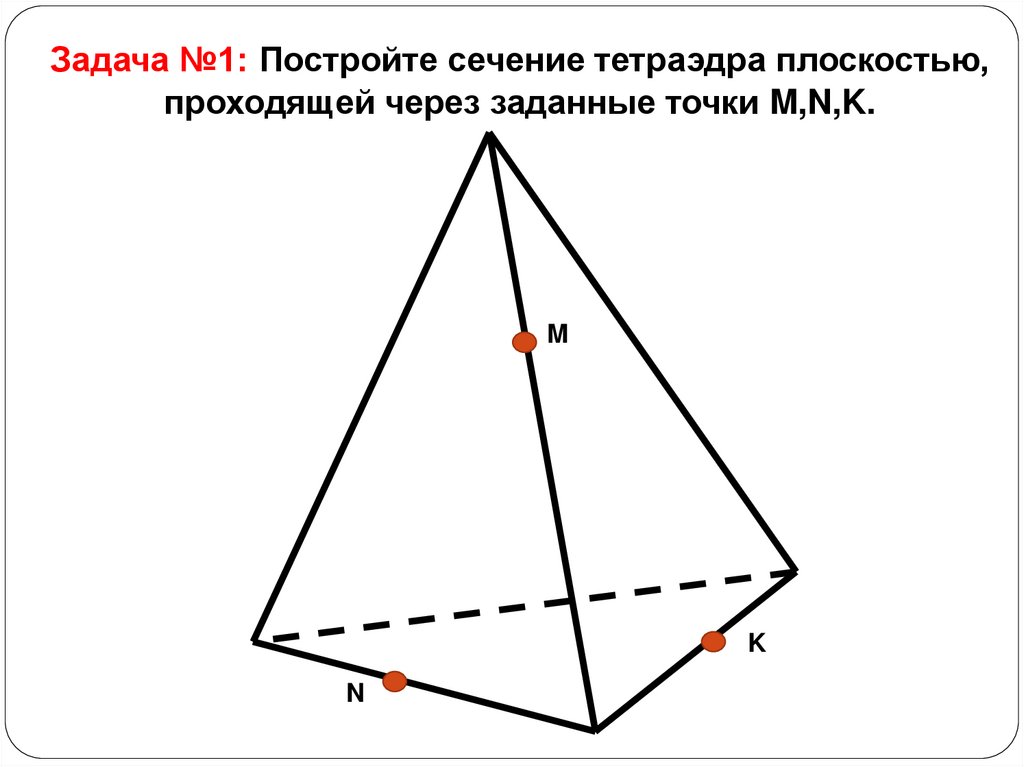
Задача №1: Постройте сечение тетраэдра плоскостью,
проходящей через заданные точки M,N,K.
M
K
N

11.

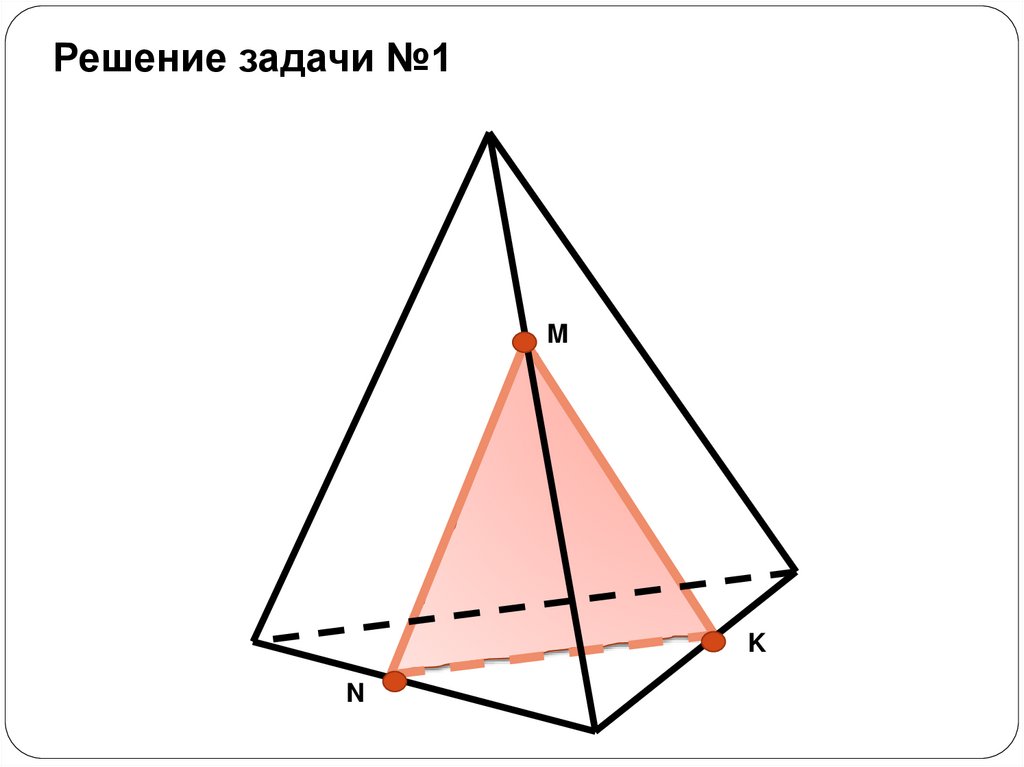
Решение задачи №1
M
K
N

12.

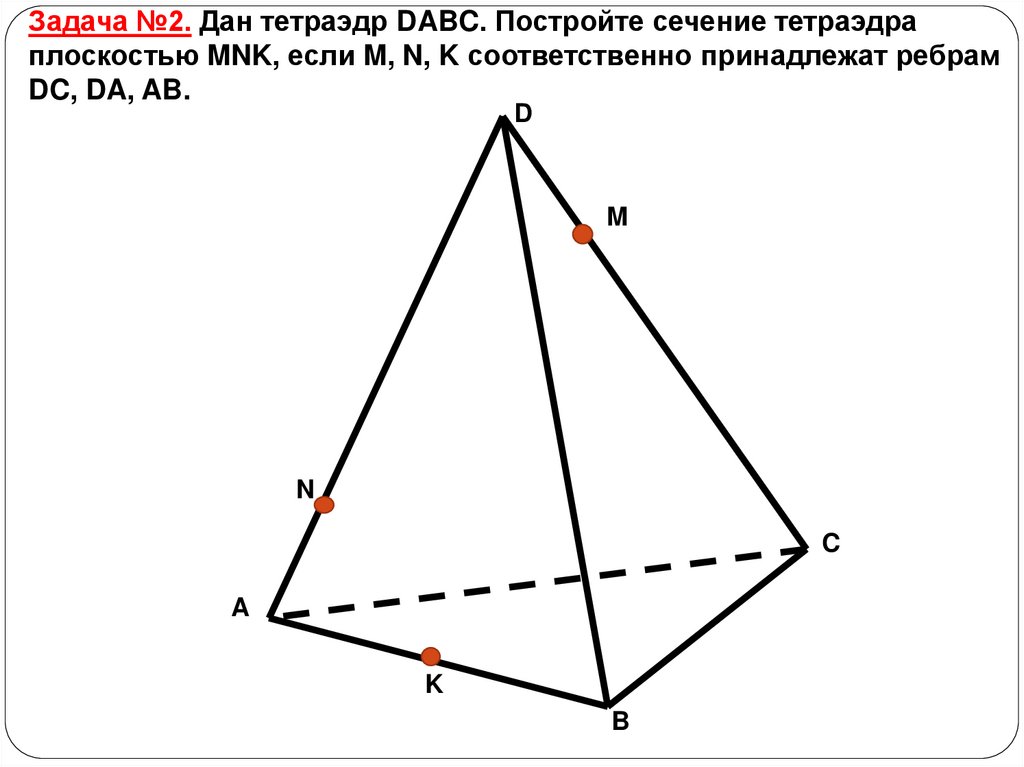
Задача №2. Дан тетраэдр DABC. Постройте сечение тетраэдра
плоскостью MNK, если M, N, K соответственно принадлежат ребрам
DC, DA, AB.
D
M
N
C
A
K
B

13.

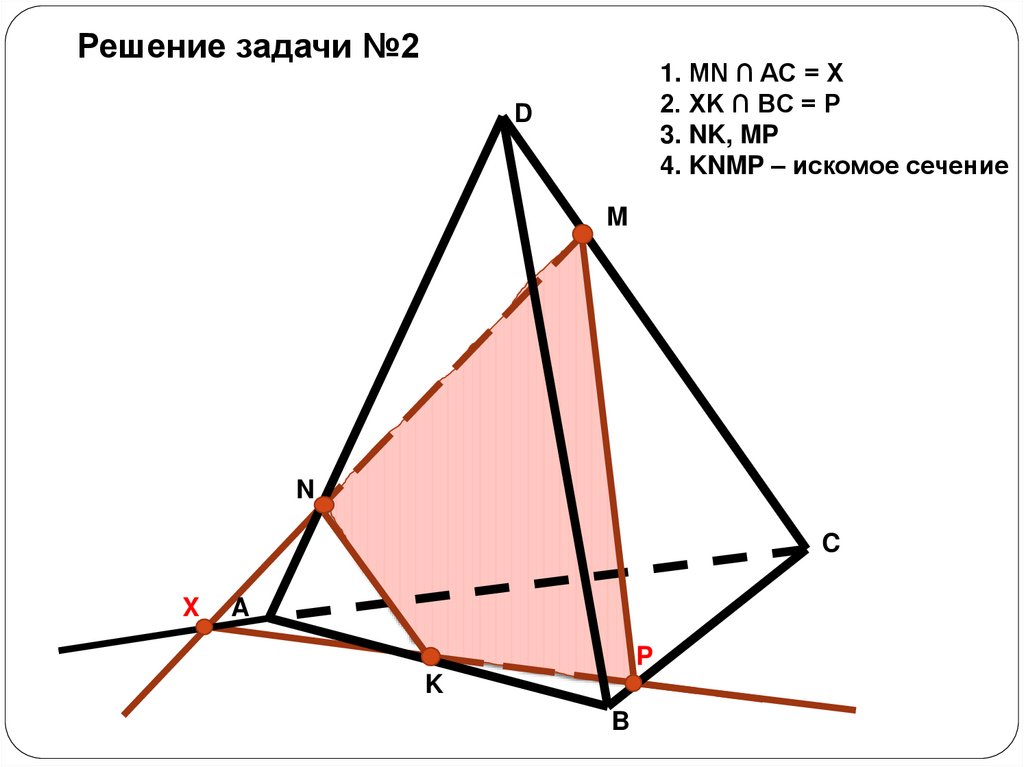
Решение задачи №2
1. MN ∩ AC = X
2. XK ∩ BC = P
3. NK, MP
4. KNMP – искомое сечение
D
M
N
C
X
A
P
K
B

14.

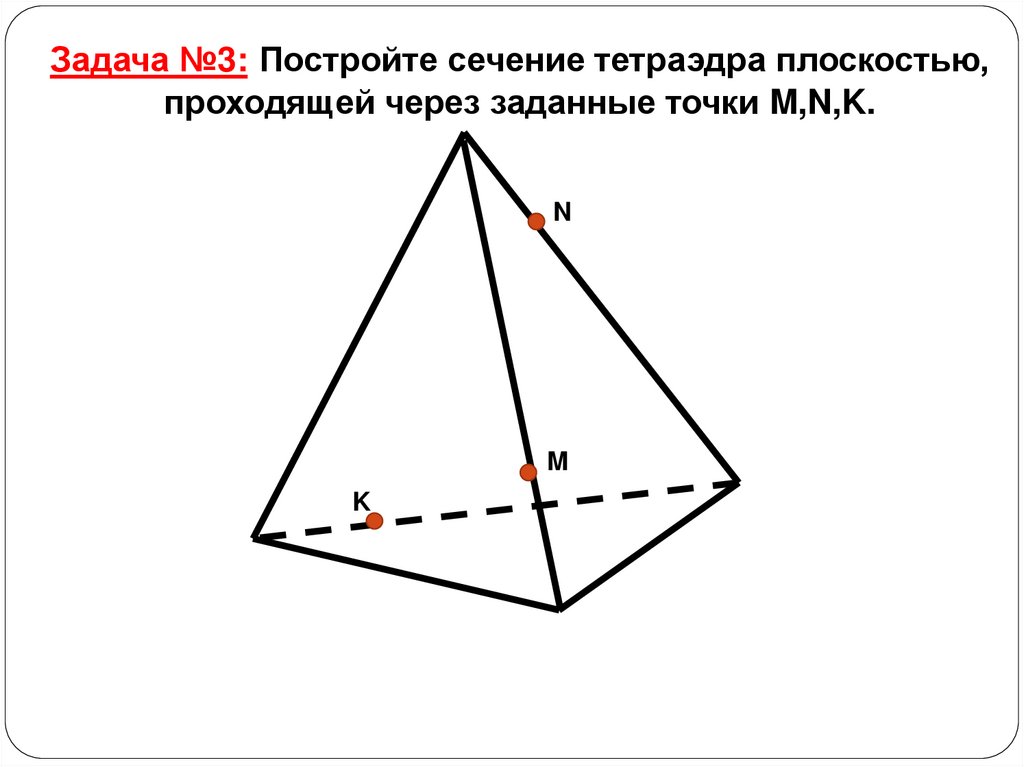
Задача №3: Постройте сечение тетраэдра плоскостью,
проходящей через заданные точки M,N,K.
N
M
K

15.

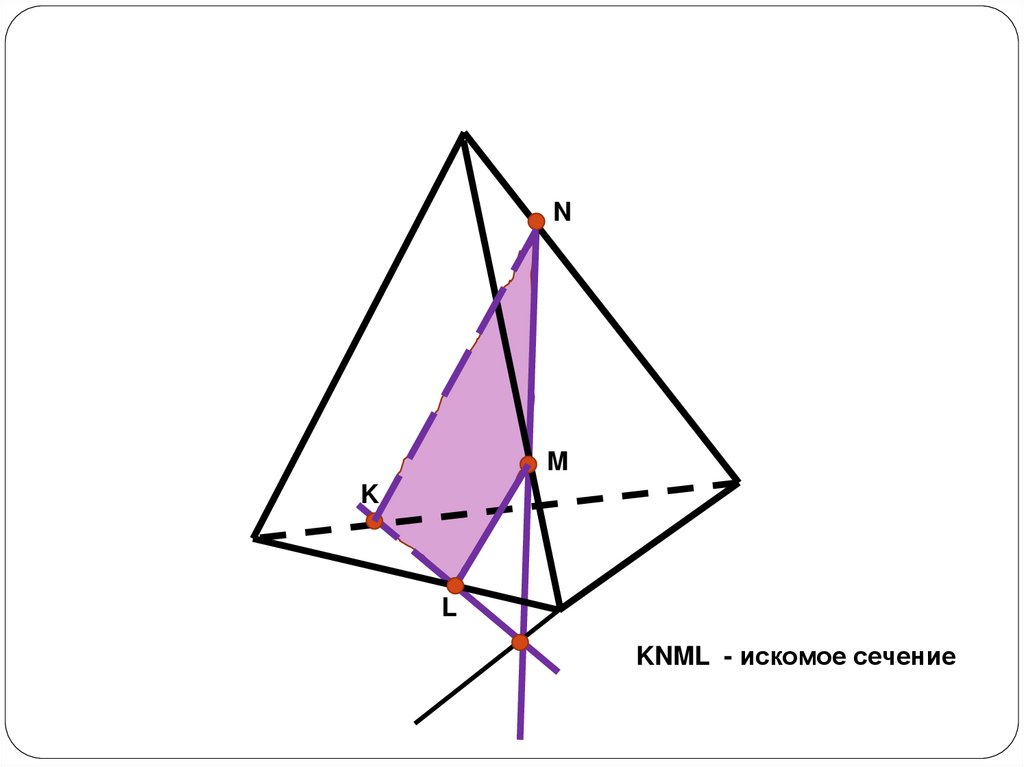
N
M
K
L
KNML - искомое сечение

16.

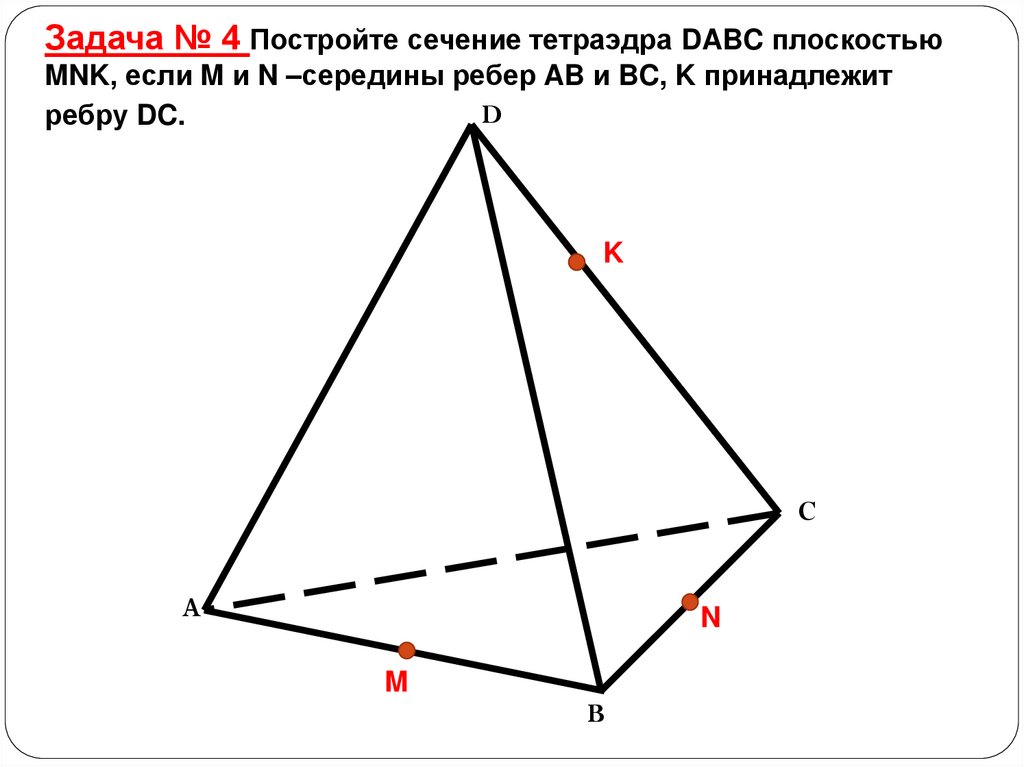
Задача № 4 Постройте сечение тетраэдра DABC плоскостью
MNK, если M и N –середины ребер AB и BC, K принадлежит
D
ребру DC.
K
C
A
N
M
B

17.

1. MN
2. NK
3. LK II MN
4. ML
5. MNKL – искомое сечение
D
K
L
C
A
N
M
B