Виробничі функції в землевпорядному проектуванні. Етапи моделювання та критерії оптимальності. Лек. 2

1. Виробничі функції в землевпорядному проектуванні. Етапи моделювання та критерії оптимальності

ВИРОБНИЧІ ФУНКЦІЇ В ЗЕМЛЕВПОРЯДНОМУ
ПРОЕКТУВАННІ.
ЕТАПИ МОДЕЛЮВАННЯ ТА КРИТЕРІЇ
ОПТИМАЛЬНОСТІ
к.е.н., доцент Тимошевський В.В.

2. ФУНКЦІЯ

3. Залежність змінної y від змінної x називається функцією, якщо кожному значенню x відповідає єдине значення y. При цьому x

називають аргументом
(незалежною змінною), y - функцією (залежною
змінною).
Записують цю відповідність наступним чином:
y=f(x)

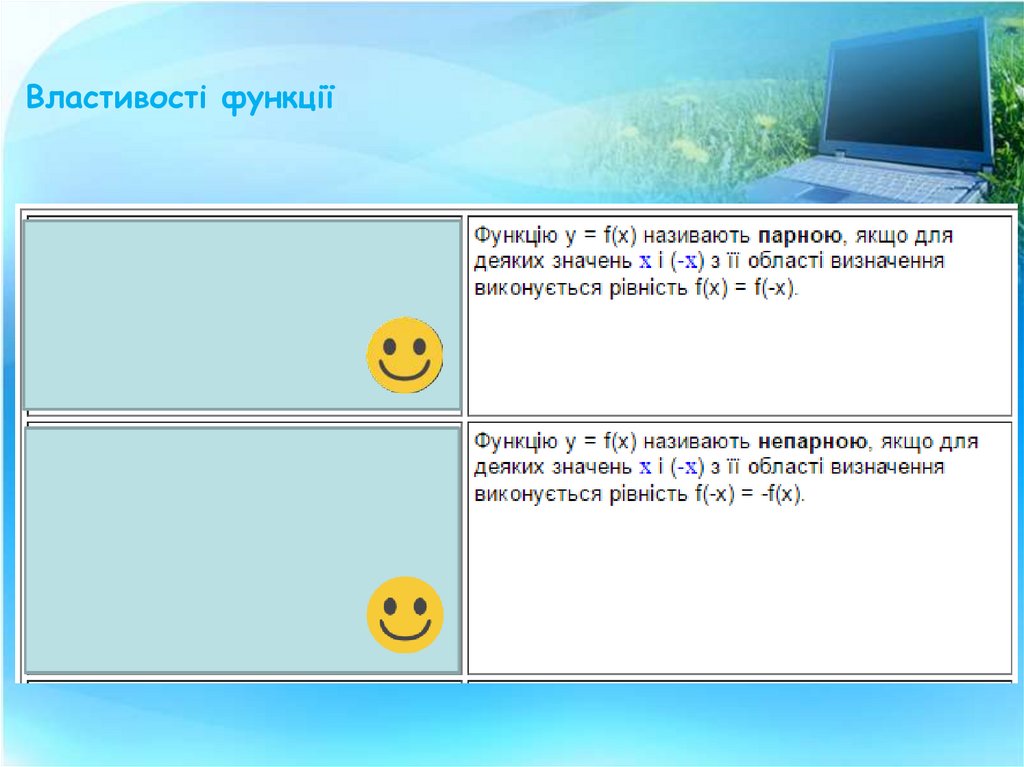
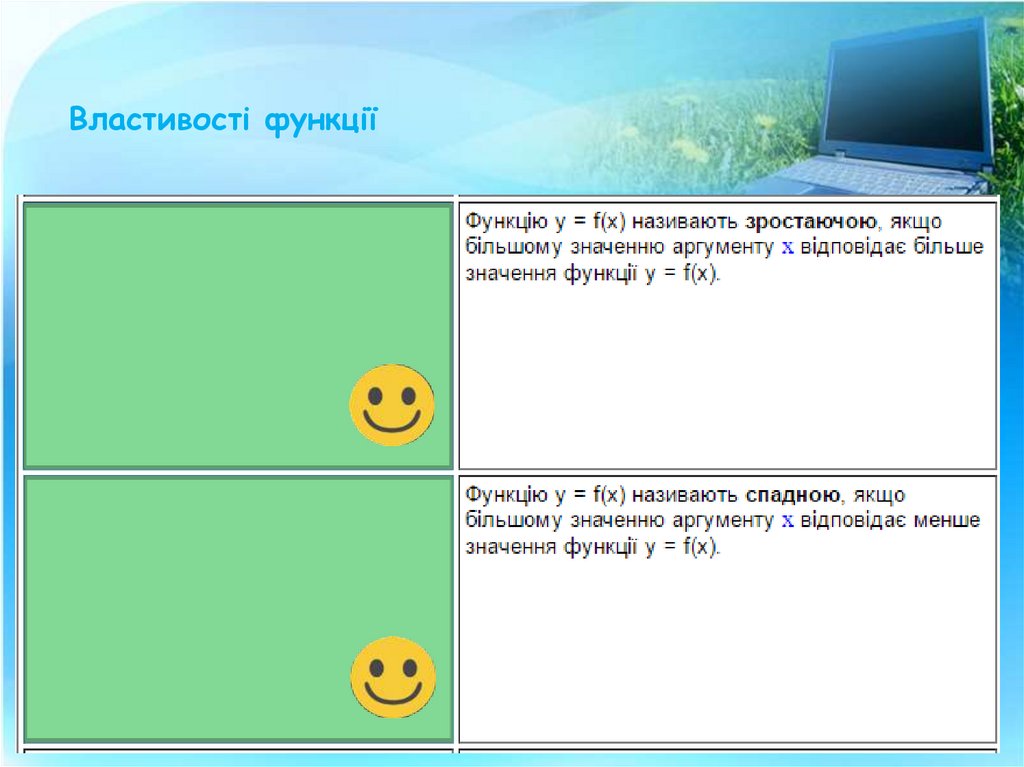
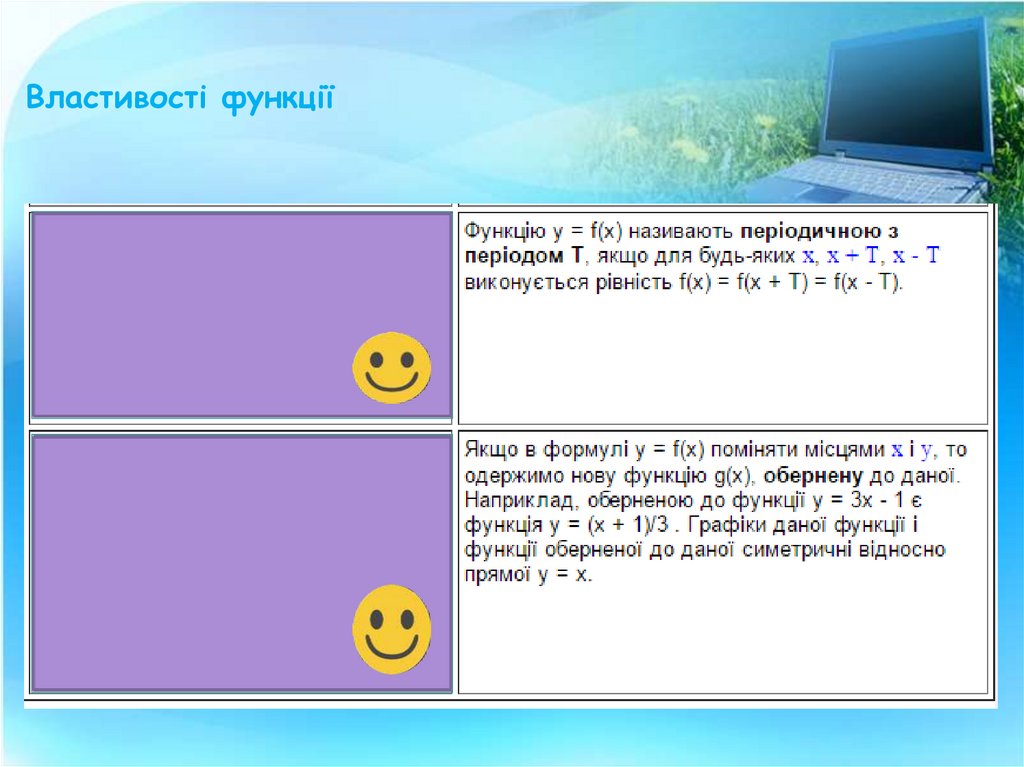
4. Властивості функції

5.

Властивості функції

6. Властивості функції

7. Якщо при деякому x функція y = f(x) набуває найбільшого значення, то цю точку називають точкою максимуму цієї функції. Якщо в

точці x функція y = f(x) набуває
найменшого значення, то цю точку
називають точкою мінімуму функції.
Точки максимуму і точки мінімуму
називають точками екстремуму функції.

8. Диско алгебра

9. Кожна економічна система має мету (ціль) розвитку та функціонування. Ступінь досягнення мети, здебільшого, має кількісну міру,

тобто може бути описаний
математично.
Нехай F – обрана мета (ціль). За цих умов вдається, як
правило, встановити залежність між величиною F, якою
вимірюється ступінь досягнення мети, і незалежними
змінними та параметрами системи

10. Функцію F називають цільовою функцією. Для економічної системи це є функція ефективності її функціонування та розвитку,

оскільки значення F
відбиває ступінь досягнення певної мети.
Задача математичного моделювання полягає у
знаходженні таких значень змінних щоб цільова
функція набувала екстремального (максимального чи
мінімального) значення.

11. Обмеженість тих або інших ресурсів можна описати системою математичних рівнянь та нерівностей Набір символів {≤,=,≥} означає,

що для деяких значень поточного
індексу r виконуються нерівності типу ≤, для інших – рівності
(=), а для решти – нерівності типу ≥.

12. Система називається системою обмежень, або системою умов задачі. Вона описує внутрішні технологічні та економічні процеси

функціонування й розвитку виробничоекономічної системи, а також процеси
зовнішнього середовища, які впливають на
результат діяльності системи.
Для економічних систем змінні Xj мають бути
невід'ємними:

13. Вирази є економіко-математичною моделлю економічної системи.

14. При моделюванні, особливо при формалізованому записі умов завдання, використовують різні символічні позначення. З формальних

позицій не має значення, якими символами
будуть позначатися окремі параметри моделі, головне,
щоб вони мали чіткий та однозначний сенс.
Але такий підхід не завжди сприяє гарному сприйняттю
модельних записів, так як доводиться постійно
відволікатися в пошуках тлумачення символів.
Тому слід вважати розумним найчастіші параметри
моделей позначати загальноприйнятими символами і
індексами і тільки в окремих випадках залучати нові
символи, з додатковими поясненнями.

15. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

ІНДЕКСИ
n - загальна кількість змінних, що позначають шукані
інтенсивності (шуканий розвиток, розміри) видів
діяльності;
j - номер змінної (порядковий номер галузі, виду
діяльності тощо)
J – множина змінних
m - загальна кількість обмежень, які визначають
умови вирішення завдання, баланс ресурсів,
виробництво продукції тощо
і - порядковий номер обмежень
І - множина обмежень

16. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

КОЕФІЦІЄНТИ
Коефіцієнти - величини, що характеризують
розміри витрат-випуску в розрахунку на
одиницю розмірності, прийнятої для шуканої
змінної.
Коефіцієнти супроводжуються індексами
приналежності, перший з них позначає
приналежність до обмежень, наступний до
змінних.

17. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

КОЕФІЦІЄНТИ
Для позначення будь-яких видів витрат,
випуску продукції тощо може прийматися
коефіцієнт а
Наприклад аij – розміщення і-тої с.-г.
культури на j-тій агровиробничій групі
грунтів

18. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

КОЕФІЦІЄНТИ
Коефіцієнти цільової функції позначають
символом с, з відповідними індексами
приналежності до змінної.
Сумарне значення цільової функції
позначають символами С і F

19. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

КОНСТАНТИ
Константами називають величини, що
представляють значення правих частин
рівнянь і нерівностей, що моделюють
систему.
Індекси при символах константах
відповідають індексам обмежень

20. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

КОНСТАНТИ
b - орні угіддя;
b’ - землі сільськогосподарського призначення;
b’’ - природні сіножаті;
D - трудові ресурси;
А - сільськогосподарська техніка;
Н - основні виробничі фонди;
R - виробництво продукції;
L - матеріальні ресурси;
S - грошові ресурси;
Q - кормові ресурси;
N. Р, К - добрива за видами

21. Як «загальноприйняті» індекси, символи та змінні можуть використовуватися наступні

ЗМІННІ
Шукані змінні, що представляють види діяльності,
зазвичай позначають символом х.
Додаткові шукані змінні можна позначати тим же
символом з рисками, іншими додатковими
позначеннями

22. Розробляючи модель, слід керуватися певними правилами: 1. Модель має адекватно описувати реальні технологічні та економічні

процеси.
2. У моделі потрібно враховувати все істотне,
суттєве в досліджуваному явищі чи процесі,
нехтуючи всім другорядним, неістотним у
ньому.

23. Математичне моделювання – це мистецтво, вузька стежка між переспрощенням та переускладненням. Справді, прості моделі не

забезпечують відповідної
точності, і «оптимальні» розв'язки за такими
моделями, як правило не відповідають реальним
ситуаціям, дезорієнтують користувача, а
переускладнені моделі важко реалізувати як з огляду на
неможливість інформаційного забезпечення, так і через
відсутність відповідних методів оптимізації.

24. 3. Модель має бути зрозумілою для користувача, зручною для реалізації. 4. Потрібно забезпечити, щоб множина наборів Хj була не

порожньою.
З цією метою в економіко-математичних моделях по змозі
слід уникати обмежень типу «=», а також суперечливих
обмежень. Наприклад, ставиться обмеження щодо виконання
контрактів, але ресурсів недостатньо, аби їх
виконати. Якщо система має єдиний розв'язок, то не існує
задачі вибору оптимального плану.

25. Будь-яка класифікація передбачає вибір критерію, згідно з яким вона здійснюється. Оскільки математичне програмування передусім

класифікація задач математичного програмування
Будь-яка класифікація передбачає вибір критерію,
згідно з яким вона здійснюється.
Оскільки математичне програмування передусім є
строгою математичною дисципліною, то критеріями
класифікації мають бути в основному математичні
структури (властивості) задач і методів їх
розв'язування.
Зауважимо, що одна й та сама задача з погляду різних
математичних критеріїв може належати до кількох
класів.

26. Задачі математичного програмування поділяються на два великі класи лінійні та нелінійні. Якщо цільова функція та обмеження є

лінійними
функціями, тобто вони містять змінні у першому
або нульовому степені.
В усіх інших випадках задача буде нелінійною.
Важливою перевагою лінійних задач є
те, що для їх розв'язування розроблено
універсальний метод, який називається
симплексним методом.

27. Економічні та технологічні процеси, як правило, є нелінійними, стохастичними, розвиваються в умовах невизначеності. Лінійні

економіко-математичні моделі часто є
неадекватними, а тому доводиться будувати нелінійні та
стохастичні моделі. Розв'язувати нелінійні задачі набагато
складніше, ніж лінійні, оскільки немає універсального
методу розв'язування таких задач.
Для окремих типів нелінійних задач розроблено численні
спеціальні ефективні методи розв'язування. Проте слід
зазначити, що на практиці застосовують, здебільшого,
лінійні економіко-математичні моделі.
Часто нелінійні залежності апроксимують (наближають)
лінійними. Такий підхід на практиці є доволі ефективним.

28. У нелінійному програмуванні виокремлюють такий клас як опукле програмування. Для задач опуклого програмування існує низка добре

обґрунтованих та ефективних методів їх
розв'язування.
Задачі лінійного програмування є частковим
випадком задач опуклого програмування.

29. Квадратичне програмування – цільова функція квадратична, а обмеження лінійні.

30. Задачі математичного програмування поділяють на дискретні і неперервні. Дискретними називають задачі, в яких одна, кілька або

всі змінні набувають лише дискретних значень.
Окремий клас становлять задачі, в яких одна або
кілька змінних набувають цілочислових значень,
тобто задачі цілочислового програмування.
Якщо всі змінні можуть набувати будь-якого
значення в деяких інтервалах числової осі, то задача
є неперервною.

31. Задачі математичного програмування поділяються також на детерміновані і стохастичні. Детерміновані задачі не містять випадкових

змінних і
параметрів, котрі набувають значень відповідно до функції
розподілу.
У противному разі адекватна економіко-математична модель
має бути стохастичною, тобто містити випадкові функції та
величини. Структура та розв'язування таких задач
вивчаються в окремому розділі, який називається
стохастичним програмуванням.

32. Особливий клас становлять задачі теорії ігор, які широко застосовуються в ринковій економіці. Адже тут діють дві чи більше

конфліктних
сторін, які мають цілі, що не збігаються, або
протилежні цілі.

33. Математичне моделювання економічних процесів передбачає наступні етапи: 1) вивчення сутності економічного процесу з

літературних джерел і
на конкретному прикладі;
2) постановка економіко-математичної задачі;
3) вибір математичного методу вирішення задачі;
4) формалізація планово-економічної задачі;
5) аналіз кількісних залежностей параметрів задачі;
6) побудова структурної математичної моделі задачі;
7) отримання, обробка та встановлення достовірності необхідної
інформації;
8) побудова розширеної економіко-математичної моделі задачі та її
корегування в метод вирішення;
9) вирішення задачі;
10) аналіз результатів вирішення задачі і корегування економікоматематичної задачі;
11) вирішення задачі по скорегованій моделі;
12) економічний аналіз різних варіантів і вибір проекту розвитку
економічного процесу.

34. Моделювання економічного процесу треба починати з ретельного вивчення його за різними джерелами інформації. При цьому необхідно

виявити зовнішні і
внутрішні зв’язки економічного процесу.

35. Великого значення набуває правильна постановка економіко-математичної задачі. Слід добре знати обчислювальні можливості

існуючих математичних
методів.
В постановці задачі повинна бути чітка
відповідь, що в ній є невідомим, що треба
шукати, яка переслідується мета, на які
питання необхідно відповісти, які відносини
треба передбачити.

36. Вибір математичного методу вирішення задачі залежить від розвитку вичислювальної математики і класу задачі. Одним із методів,

що є найбільш розробленим і
доступним є методи лінійного програмування.

37. При формалізації економічного процесу слід встановити перелік його характеристик і проаналізувати їх зв’язки. Розробка

математичної моделі задачі передбачає побудову
спеціальної таблиці, в якій всі економічні, технологічні і інші
умови і вимоги представлені у вигляді системи нерівностей
і рівнянь, які об’єднані єдиною цільовою функцією.

38. Послідовність побудови економіко-математичної моделі може бути різною, але найбільш доцільно спочатку сформувати критерій

Послідовність побудови економікоматематичної моделі може бути різною,
але найбільш доцільно спочатку сформувати
критерій оптимальності і побудувати цільову
функцію, потім визначити види виробничої
діяльності та їх інтенсивність, встановити
склад обмежень і розробити техніко-економічні
коефіцієнти.

39. Вибір критерію оптимальності диктується економічною сутністю задачі. Він формується у вигляді функції від вхідних і вихідних

змінних, від параметрів задачі,
значення якої досягає максимуму або мінімуму
при заданих конкретних умовах, які враховані в
моделі.

40. Вибір і обґрунтування критеріїв оптимальності для обґрунтування проекту землеустрою тощо - одна з найбільш важливих, складних і

недостатньо розроблених
проблем теорії оптимального управління.
Оптимальне управління передбачає, що з усіх можливих
при сформованих умовах рішень вибирається найкраще,
що забезпечує найкращий варіант розвитку системи.
Оптимальність системи - це найкращий її стан, що
відповідає меті її функціонування в процесі розвитку.

41. Поняття «найкраще рішення», «найкращий варіант плану», «найкращий стан системи» і т.п. страждають невизначеністю, вимагають

конкретизації.
Необхідно їх кількісне вираження, що
дозволяє математично формалізувати
процес вибору найкращих рішень.

42. Принцип оптимальності в загальному вигляді полягає в досягненні заданої мети розвитку системи з найбільшою при заданих умовах

ефективністю.
Оптимум існує лише відносно конкретного
показника ефективності.

43. Проблема критеріїв оптимальності пов'язана з необхідністю розгляду наступних двох аспектів: 1. Визначення сутності економічної

категорії «критерій
оптимальності», що безпосередньо пов'язано з поняттям мети
функціонування тієї чи іншої економічної системи, частини її або
деякого економічного процесу в конкретних умовах і в даний
період розвитку.
2. Розробка економіко-математичних методів оптимізації
економічних процесів (явищ), яка пов'язана з необхідністю
визначення спеціальних показників якості критеріїв, то
екстремальних значень яких оцінювалася б порівняльна
ефективність тих чи інших варіантів рішень, планів. Інакше кажучи,
потрібні суворі правила вибору найкращого варіанта з багатьох
можливих (допустимих в даних умовах) рішень.

44. Поняття «критерій оптимальності» не слід ототожнювати з поняттям «мета системи». Мета функціонування - це деякий бажаний стан

економічної системи і тому в змістовному відношенні
істотно ширше поняття критерію оптимальності
функціонування системи.
Досягнення мети завжди, пов'язане з певними
витратами. Співвідношення ж витрат і досягнутих
результатів утворюють систему показників
ефективності функціонування системи в процесі
руху до заданої мети.

45. Критерій оптимальності є показником якості, показником ефективності функціонування системи з точки зору досягнення заданої

мети.

46. Аналітична форма вираження критерію оптимальності називається цільовою функцією (функціоналом, функцією цілі) процесу

економіко-математичної моделі