Similar presentations:
Економіка та сучасний правовий процес в землеустрої. Лек. 1
1. Економіка та сучасний правовий процес в землеустрої
к.е.н., доцент Тимошевський В.В.2. Поняття про моделі і моделювання. Економіко-математичні методи і моделі в землеустрої
ПОНЯТТЯ ПРО МОДЕЛІ ІМОДЕЛЮВАННЯ.
ЕКОНОМІКО-МАТЕМАТИЧНІ
МЕТОДИ І МОДЕЛІ В
ЗЕМЛЕУСТРОЇ
3. Термін «модель» походить від латинського modulus — зразок, норма, міра.
4. Найбільш відомі три типи моделей: геометричні, фізичні, математичні.
5. Геометричні моделі представляють деякий об'єкт, геометрично подібний до свого прототипу (оригіналу). Вони дають зовнішню уяву
про оригінал і здебільшого служать длядемонстраційних цілей.
6. Фізичні моделі відбивають подобу між оригіналом і моделлю не тільки з погляду їх форми й геометричних пропорцій, але й з
погляду фізичних процесів, що відбуваються вних. По своїй природі вони можуть бути
механічними, гідравлічними, електричними.
7. Математичні моделі являють собою абстрактні описи об'єктів, явищ або процесів за допомогою знаків (символів), тому їх називають
також абстрактними або знаковими.8. Всі моделі володіють рядом загальних властивостей: вони подібні до досліджуваного об'єкта й відбивають його найбільш істотні
сторони;при дослідженні моделі здатні заміщати
досліджуваний об'єкт, явище або процес;
вони подають інформацію не тільки про сам
об'єкт моделювання, але й про його
передбачуване поводження при умовах, що
змінюються.
9. Mодель – це такий матеріально або розумово зображуваний об’єкт, який у процесі дослідження зaмінює об’єкт-оригінал таким чином,
що його безпосереднє вивчення даєнові знання про цей об’єкт.
10. В означенні моделі можна визначити декілька важливих моментів: • модель може бути матеріальним об’єктом або абстрактним
представленням, і, як наслідок, конкретневтілення моделі не буде суттєвим для мети
моделювання;
• основна властивість моделі – здатність представити
об’єкт при дослідженні його властивостей;
• моделлю може бути тільки така структура, яка
дозволить отримати на її основі більш повну
інформацію, в порівнянні з безпосереднім
дослідженням об’єкта.
11. Моделювання у вузькому змісті - побудова моделі об'єкта, що досліджується, явища або процесу. Об'єкт — це фізичне (матеріальне)
тіло, річ.Явище — це зовнішні властивості й ознаки
предмета, що осягаються через відчуття,
сприйняття, подання.
Процес — це хід, розвиток явища, послідовна
зміна станів об'єкта.
12. Метод «проб і помилок» у наші дні непридатний, дуже мало часу залишається для «проб» і досить дорогими можуть бути «помилки».
13. Під математичним моделюванням розуміється опис реальної дійсності в математичній формі, тобто математична модель - це
математичнасистема, що описує певними знаками та
символами об'єкти, явища, ті чи інші економічні
процеси.
Математичні моделі в економіці прийнято
називати економіко-математичними.
Економіко-математична модель завжди не є точною
копією, а деякою схемою, абстракцією економічного
процесу.
14. При розробці економіко-математичних моделей застосовується принцип так званого гомоморфізму. Так гомоморфізм, або гомоморфне
відображення, групи G нагрупу Н є відображенням, при якому кожному елементу g з групи
G належить елемент h з групи Н (так званий образ g); такий,
що кожен елемент з Н є образом деякого елемента з G, і
добутку (сумі) двох елементів з G відповідає добуток (сума) їх
образів.
Гомоморфний образ – це неповне, приблизне
відображення структури оригіналу.
15. Мета моделювання полягає у знаходженні оптимального поєднання змінних, що дають найкращий результат за обраним критерієм
оптимальності.Цільова функція є залежністю узагальненого
показника від параметрів моделі. Залежно від
обраного критерію оптимальності напрямок
оптимізації виражається у формі максимізації
або мінімізації цільової функції.
16. Економіко-математичні моделі дозволяють знаходити оптимальні (мінімальні, максимальні) значення цільових функцій, яким
відповідають певні числові характеристикипроектних землевпорядних рішень, отримані з
урахуванням обмеженості ресурсів.
Лімітуючими (цінними) ресурсами при
побудові моделей є гроші, матеріали, праця,
земля.
17. Математична модель являє собою систему нерівностей і рівнянь, що зв'язують параметри моделі, оптимальне сполучення яких
необхідно визначитивідповідно до визначеного критерія
оптимальності.
18. Першовідкривач лінійного програмування у світовій науці. У книжці «Економічний розрахунок найкращого використання ресурсів»
Леоні́д Віта́лійовичКанторо́вич
(1912 –1986)
Першовідкривач лінійного програмування у
світовій науці. У книжці «Економічний
розрахунок найкращого використання
ресурсів» (1959) застосував власну теорію
лінійного програмування для дослідження
широкого кола проблем планування.
За внесок у теорію оптимального розподілу
ресурсів в 1975 р. було
присуджено Нобелівську премію.
Л. Канторович серед усіх Нобелівських
лауреатів — єдиний професійний математик.
19. Linear programming (LP) emerged in the United States in the early postwar years. One may to a considerable degree see the
George Bernard Dantzig(November 8, 1914 –
May 13, 2005)
Linear programming (LP) emerged in the United
States in the early postwar years. One may to a
considerable degree see the development of LP as a
direct result of the mobilization of research efforts
during the war.
George B. Dantzig, who was employed by the US
Armed Forces, played a key role in developing the
new tool by his discovery in 1947 of the Simplex
method for solving LP problems. Linear programming
was thus a military product, which soon appeared to
have very widespread civilian applications.
The US Armed Forces continued its support of
Dantzig’s LP work, as the most widespread textbook
in LP in the 1960s, namely Dantzig (1963), was
sponsored by the US Air Force.
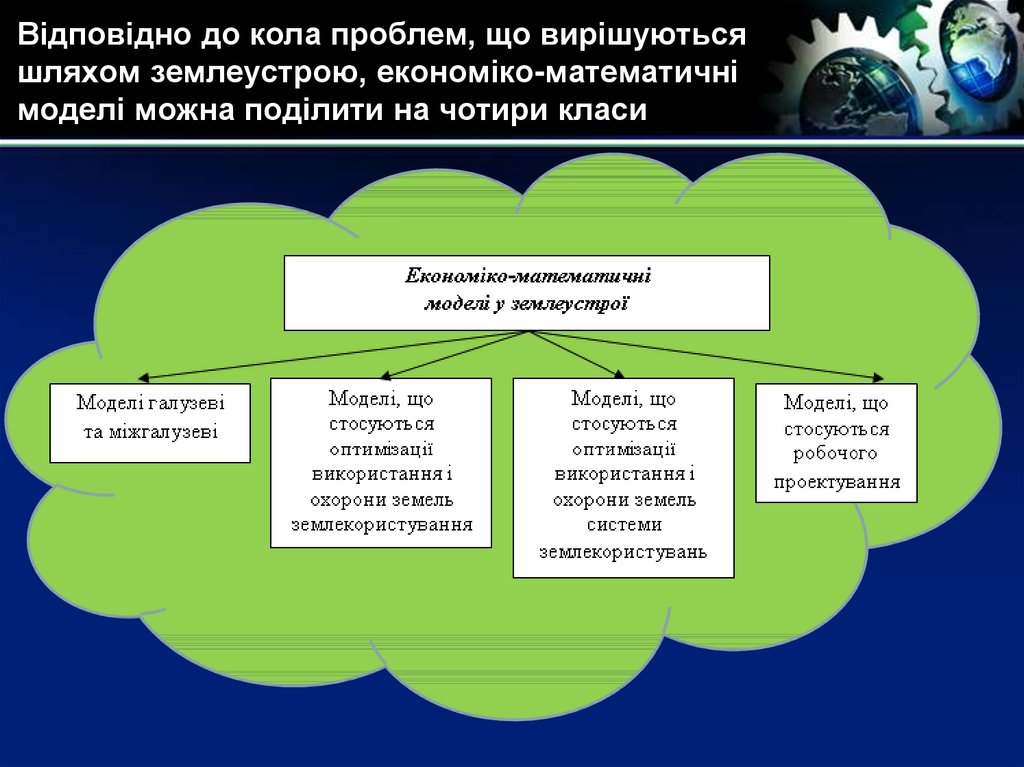
20. Відповідно до кола проблем, що вирішуються шляхом землеустрою, економіко-математичні моделі можна поділити на чотири класи
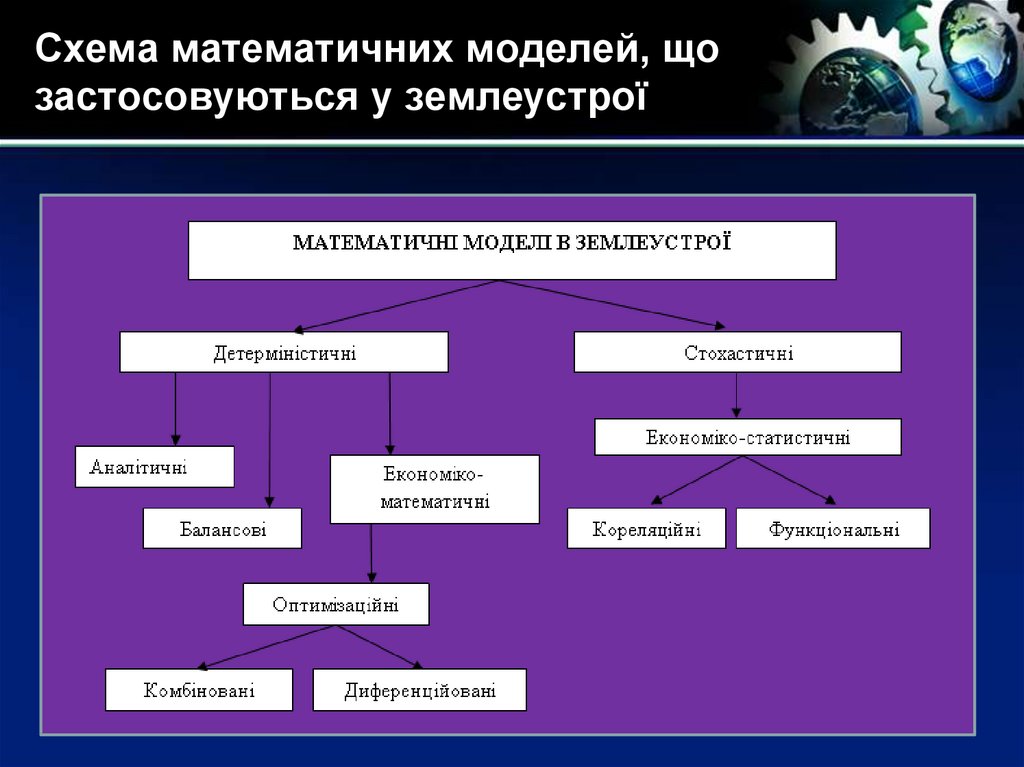
21. Схема математичних моделей, що застосовуються у землеустрої
22. Доцільність застосування економіко-математичного моделювання в землеустрої обумовлена наступними факторами: 1. Математичні
методи дозволяють знаходити найбільшдоцільні рішення щодо перерозподілу, використання та
охорони земельних ресурсів.
2. Оптимальні плани використання виробничих ресурсів,
пов'язаних із землею, сприяють досягненню заданих
обсягів виробництва при мінімальних затратах праці і
коштів.
23. 3. Результати, отримані математичними методами, дозволяють створити найкращі організаційно-територіальні умови, сприяють
3. Результати, отримані математичними методами,дозволяють створити найкращі організаційнотериторіальні умови, сприяють призупиненню
деградаційних процесів тощо.
4. Завдяки застосуванню математичних методів
поліпшується якість підготовки інформації і її
використання.
5. Застосування математичних методів сприяє не тільки
поліпшенню економічних показників, а й екологічних,
соціальних і технічних показників проекту землеустрою.
24. 6. Математичні методи, по суті, є сполучною ланкою між землеустроєм і технічними науками, що вивчають сільське господарство як
з природоохоронного, так і зекономічного і соціального боку.
7. Впровадження математичних методів
дозволить оптимізувати всю систему землеустрою
25. Класифікація математичних моделей, що використовуються у землеустрої
Класифікаційні ознакиВид проектної документації
Види моделей
Графічні
Економічні
Детерміністичні
Стохастичні
Міжгалузеві
Вид землеустрою або
Міжгосподарського землеустрою
землевпорядна дія
Внутрігосподарського землеустрою
Робочого проектування
Аналітичні (диференціального обчислення)
Економіко-статистичні (Математичної статистики)
Математичні методи, які лежать Оптимізаційні (математичного програмування)
в основі моделі
Балансові (міжгалузевого балансу)
Сіткового планування і управління
Інші
Клас проекту землеустрою
Розподіляється по класам проектів землеустрою
Ступінь визначення інформації


























 mathematics
mathematics








