Similar presentations:
Оптимізаційні економіко- математичні моделі (Лекція 2)
1. ЛЕКЦІЯ 2 ОПТИМІЗАЦІЙНІ ЕКОНОМІКО-МАТЕМАТИЧНІ МОДЕЛІ
2. План
2.1 Постановка задачі економікоматематичного моделювання.2.2 Приклади задач економікоматематичного моделювання
(самостійна робота) .
2.2.1 Задача визначення оптимального
плану виробництва.
2.2.2 Задача про «дієту».
2.2.3 Транспортна задача.
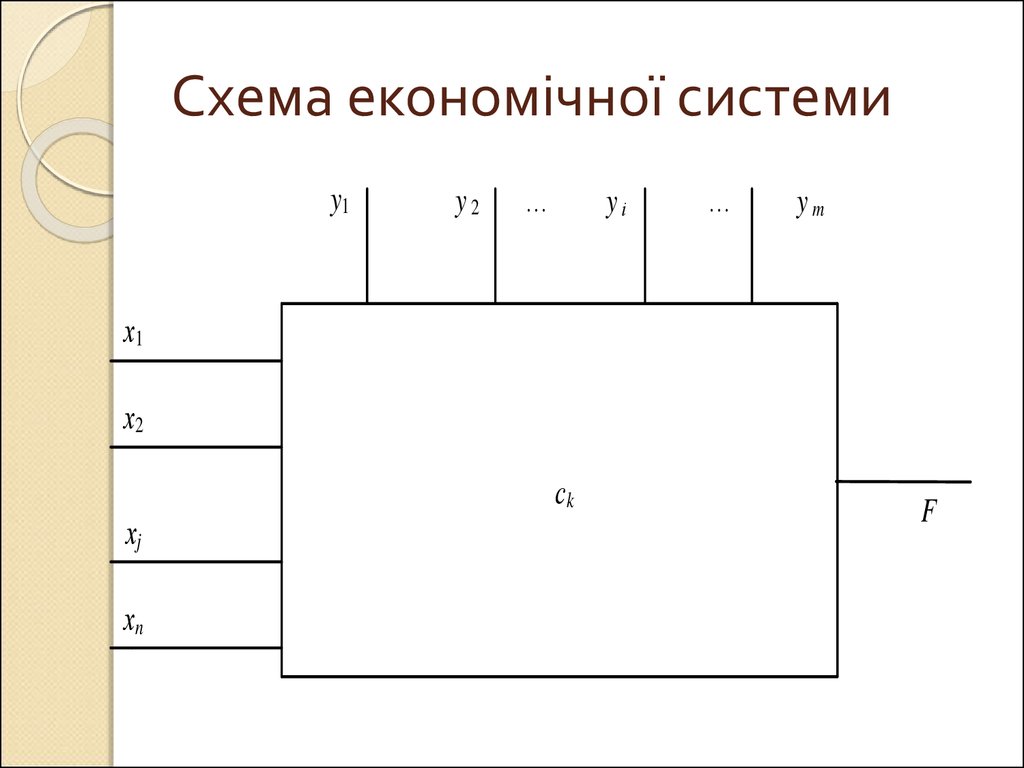
3. Схема економічної системи
y1y2
…
yі
…
ym
х1
х2
сk
хj
хn
F
4.
Цільова функція, або функція метиF = f (x1, x2,..., xn; y1, y2,..., ym; c1, c2,..., cl)
(2.1)
У загальному вигляді задача економікоматематичного моделювання формулюється
так:
Знайти такі значення керованих змінних xj, щоб
цільова функція набувала екстремального
(максимального чи мінімального значення).
max (min) F * f ( x1 , x 2 , , x n ; y1 , y 2 , , y m ; c1 , c 2 , , cl ) (2.2)
xj
5.
Система обмежень,або система умов задачі
qi ( x1 , x 2 , , x n ; y1 , y 2 , , y m ; c1 , c 2 , , cl ) , , 0;
(2.3)
(i 1, 2, , S ).
x j 0 ( j 1, 2, ..., n)
Залежності (2.2)—(2.4) утворюють
економіко-математичну модель
економічної системи.
(2.4)
6. Розробляючи економіко-математичну модель, слід дотримуватись певних правил:
1.2.
3.
4.
Модель має адекватно описувати реальні
технологічні та економічні процеси.
У моделі потрібно враховувати все істотне,
суттєве в досліджуваному явищі чи процесі,
нехтуючи всім другорядним, неістотним у
ньому.
Модель має бути зрозумілою для
користувача, зручною для реалізації на ЕОМ.
Необхідно, щоб множина змінних xj була не
порожньою.
7. Приклад Таблиця 2.1 – Інформація, необхідна для складання виробничої програми
Норми витрат на одиницюпродукції
Вид
продукції
робочого
часу,
люд.-год.
листового скла,
заліза, м2 м2
Ціна одиниці
продукції, ум. од.
Морозильна
камера
9,2
3
—
300
Електрична
плита
4
6
2
200
520
240
40
—
Загальний запас ресурсу
на місяць
8.
max F 300 x1 200 x 29,2 x1 4 x 2 520
3x1 6 x 2 240
2 x 2 40
x1 0, x 2 0
9.
m , Fi(i 1, m)
F k1 F1 k 2 F2 ... k m Fm
(2.5)
Fn 1 ,..., Fm
F1 ,..., Fn
n
F
*
Fi
i 1
m
Fi
i n 1
.
(2.6)
10.
Fi i 1, mmin F
F1 F1
F1
F2 F2
F2
...
Fm Fm
Fm
(2.7)
Fi (i 1, m)
min F k1
F1 F1
F1
k2
F2 F2
F2
... k m
Fm Fm
Fm
(2.8)
11.
FkFi zi
Fi z i
F1 max F1 F1
Математичне програмування — один із
напрямків прикладної математики,
предметом якого є задачі на знаходження
екстремуму деякої функції за певних
заданих умов.
12. Класифікація задач математичного програмування
Задачі математичного програмуванняЗадачі теорії
ігор
Детерміновані
Стохастичні
Статичні
Нелінійні
Дискретні
Лінійні
Нелінійні
Неперервні
Лінійні
Нелінійні
Дискретні
Лінійні
Нелінійні
Лінійні
Неперервні
Динамічні







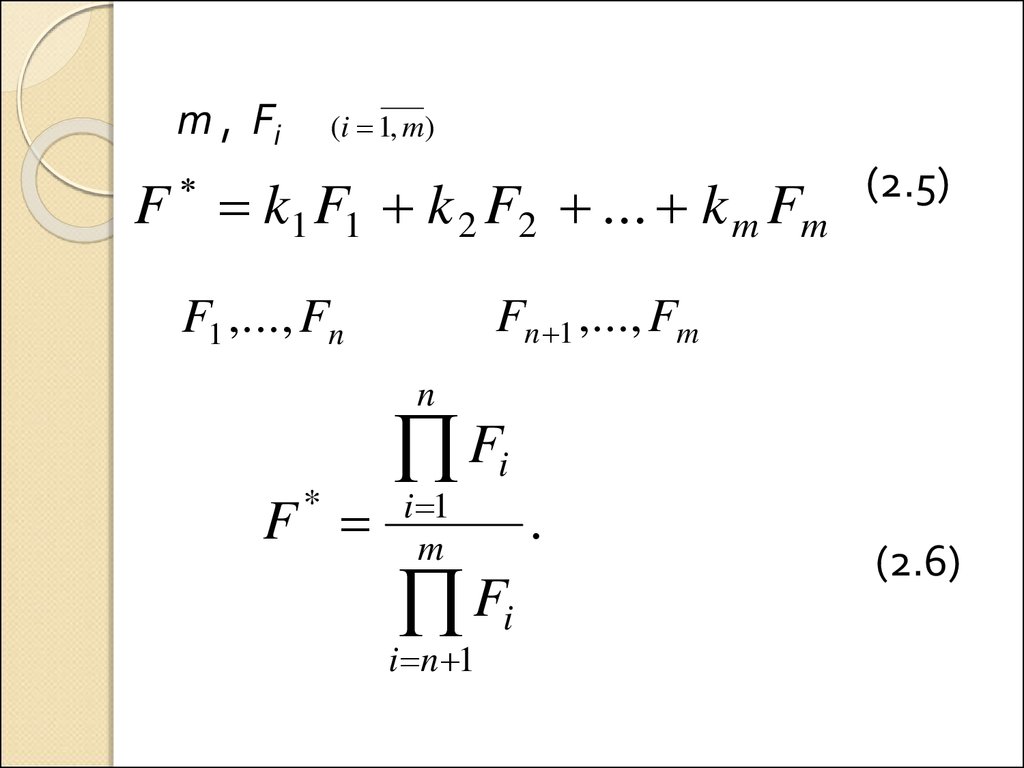



 mathematics
mathematics economics
economics








