Similar presentations:
Электростатика. Электрический заряд. Закон сохранения заряда. Закон Кулона. Электрический диполь
1. Электростатика
Лекция 1Электростатика
CEE
2.
План лекции1.1.Электрический заряд. Закон
сохранения заряда.
1.2. Закон Кулона.
1.3. Напряженность электрического поля.
1.4. Принцип суперпозиции
электрических полей.
1.5. Силовые линии электрического поля.
1.6. Электрический диполь.
CEE
3.
1.1.Электрический заряд.Закон сохранения заряда
!
Величина, количественно характеризующая способность наэлектризованных тел оказывать электрическое воздействие на другие тела
и подвергаться самим этому
воздействию, называется электрическим зарядом.
CEE
4.
1.1.Электрический заряд.Закон сохранения заряда
е – элементарный заряд.
q = ne
n – число
элементарных
зарядов.
!
mе – масса электрона.
mе = 9,1 · 10-31 кг
Любой заряд кратен элементарному.
CEE
5.
1.1.Электрический заряд.Закон сохранения заряда
H
He
– -е
е
+
2е
++
-е –
!
– -е
Li
-е –
– -е
+ 3е
++
– -е
Атом – нейтральная частица. Он состоит
из ядра и электронов. Число электронов
q− = −ze равно числу протонов в ядре q+ =
+ze (где z ─ порядковый номер элемента в таблице
Менделеева).
CEE
6.
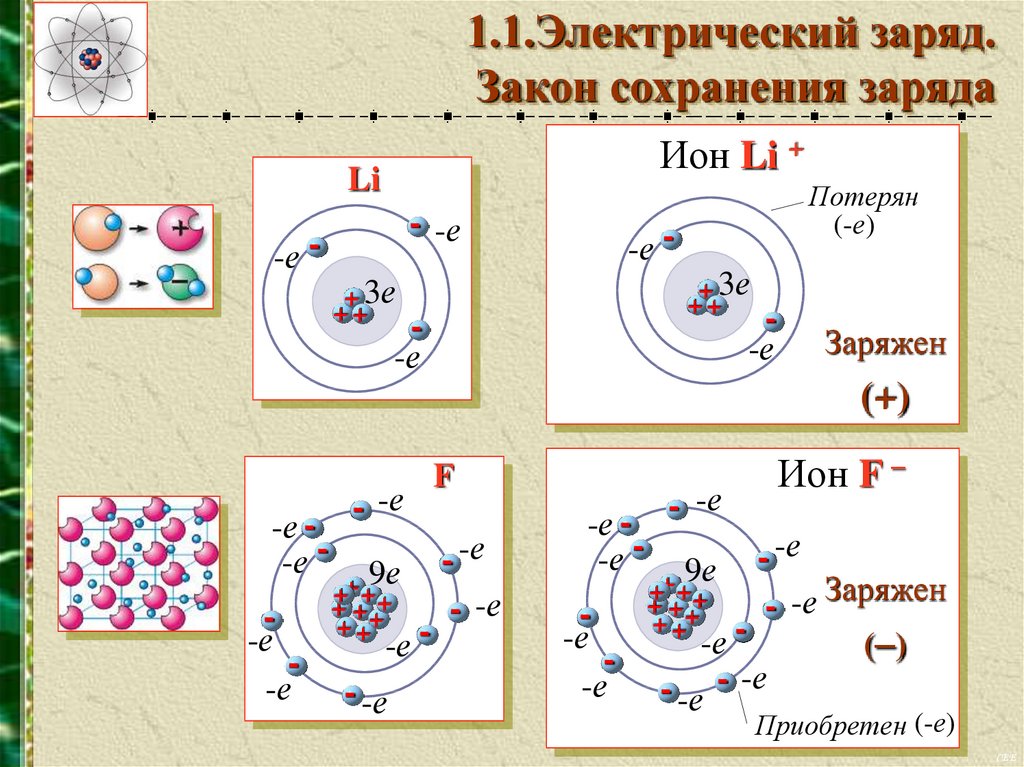
1.1.Электрический заряд.Закон сохранения заряда
Ион Li +
Li
- -е
-е -
Потерян
(-е)
-е + 3е
++
+ 3е
++
-е
-е
Заряжен
(+)
-е -е -е
-е
- -е
9е
++ + +
+ ++
++
-е -
- -е
F
- -е
- -е
-е -е -
- -е
Ион F –
-е
9е
++ + +
Заряжен
-е
+
+
+ ++ -е
-е
(– )
-е
- -е - -е
Приобретен (-е)
CEE
7.
1.1.Электрический заряд.Закон сохранения заряда
!
В замкнутой системе алгебраическая
сумма зарядов всех тел остается
постоянной.
q1 + q2 + ...+ qn = const
n
q
i 1
i
const
CEE
8.
1.2. Закон Кулона(14.VI.1736–23.VIII.1806)
Основной закон
электростатики был
экспериментально
установлен
французским физиком
Шарлем Кулоном в
1785 г.
CEE
9.
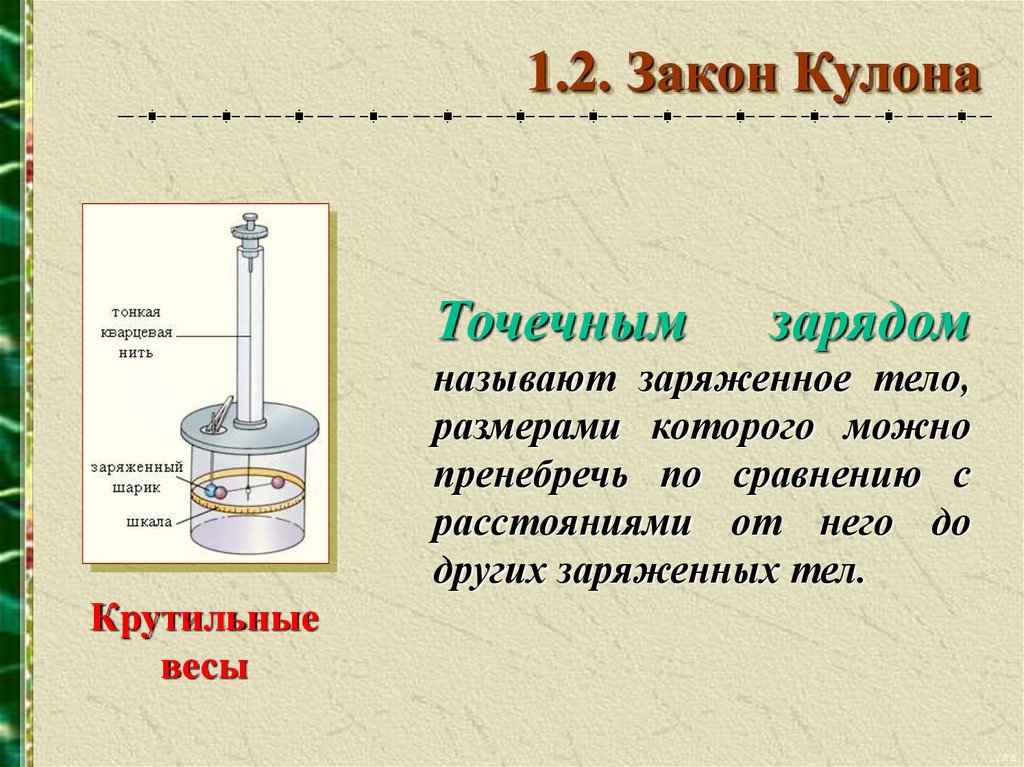
1.2. Закон КулонаТочечным
зарядом
называют заряженное тело,
размерами которого можно
пренебречь по сравнению с
расстояниями от него до
других заряженных тел.
Крутильные
весы
CEE
10.
1.2. Закон Кулона!
Сила взаимодействия двух точечных
неподвижных электрических зарядов в
вакууме
прямо
пропорциональна
произведению величин этих зарядов и
обратно пропорциональна квадрату
расстояния между ними.
CEE
11.
1.2. Закон КулонаF k
q1 q2
r
2
,
где |q1| и |q2| — модули зарядов,
r — расстояние между ними,
k
— коэффициент пропорциональности, зависящий
от выбора системы единиц.
В СИ
k = 9·109 Нּм2/Кл2.
CEE
12.
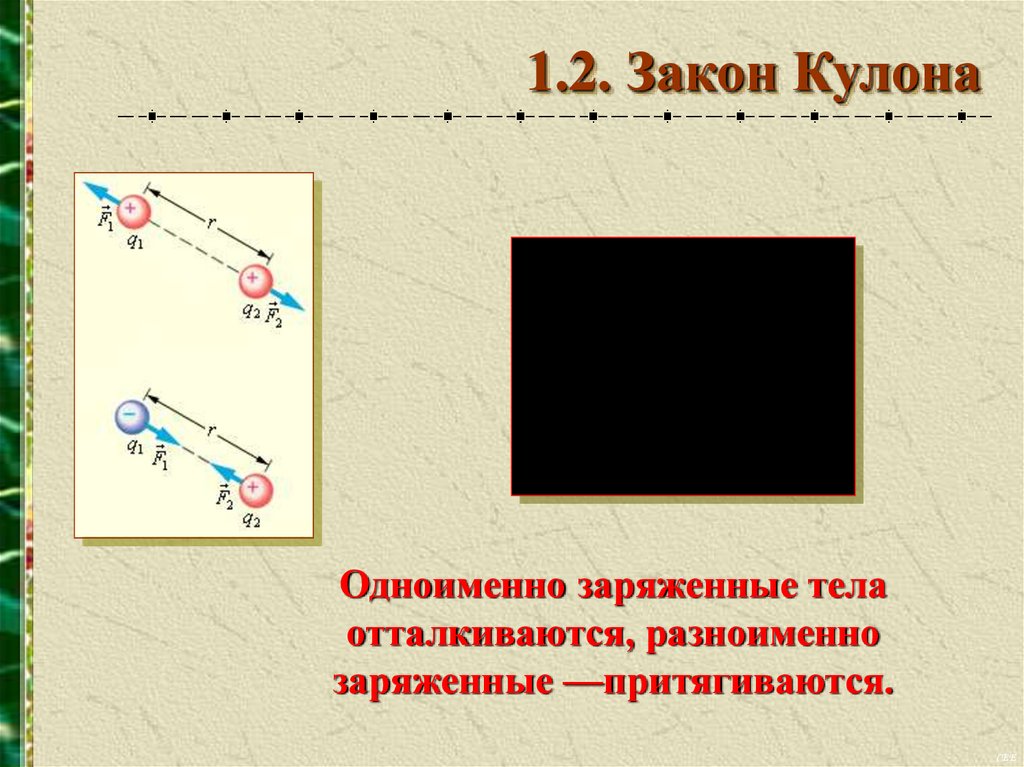
1.2. Закон КулонаОдноименно заряженные тела
отталкиваются, разноименно
заряженные —притягиваются.
CEE
13.
1.2. Закон КулонаКоэффициент k в СИ
обычно записывают в виде:
где
0 8,85 10
12
F
k
2
Kл
2
Н м
1
4 0
1
4 0
,
– электрическая
постоянная.
q1 q2
r
2
CEE
14.
1.2. Закон КулонаЗакон Кулона можно выразить в векторной форме:
1 q1q2 r
F
2
4 0 r r
или
F
q1q2
r
3
4 0 r
1
где
сила, действующая
на заряд, к которому направлен
радиус-вектор r.
─ сила, действующая на
заряд q1 со стороны заряда q2;
2 ─ сила, действующая на
заряд q2 со стороны заряда q1.
1
q1
q2
CEE
15.
1.2. Закон КулонаЕсли заряды находятся не в вакууме, а в какой-либо
непроводящей среде, то закон Кулона можно
записать в виде:
F k
где
q1 q2
r
ε
2
или
F
1
4 0
q1 q2
r
2
,
– относительная диэлектрическая
проницаемость среды.
CEE
16.
1.2. Закон КулонаПри этом направление силы в среде останется таким же,
как и в вакууме. Поэтому обобщим закон Кулона для
среды:
F
1 q1q2 r
4 0 r 2 r
В вакууме ε = 1
εε0 –
абсолютная диэлектрическая
проницаемость среды.
CEE
17.
1.2. Закон КулонаCEE
18.
1.3 Напряженностьэлектрического поля
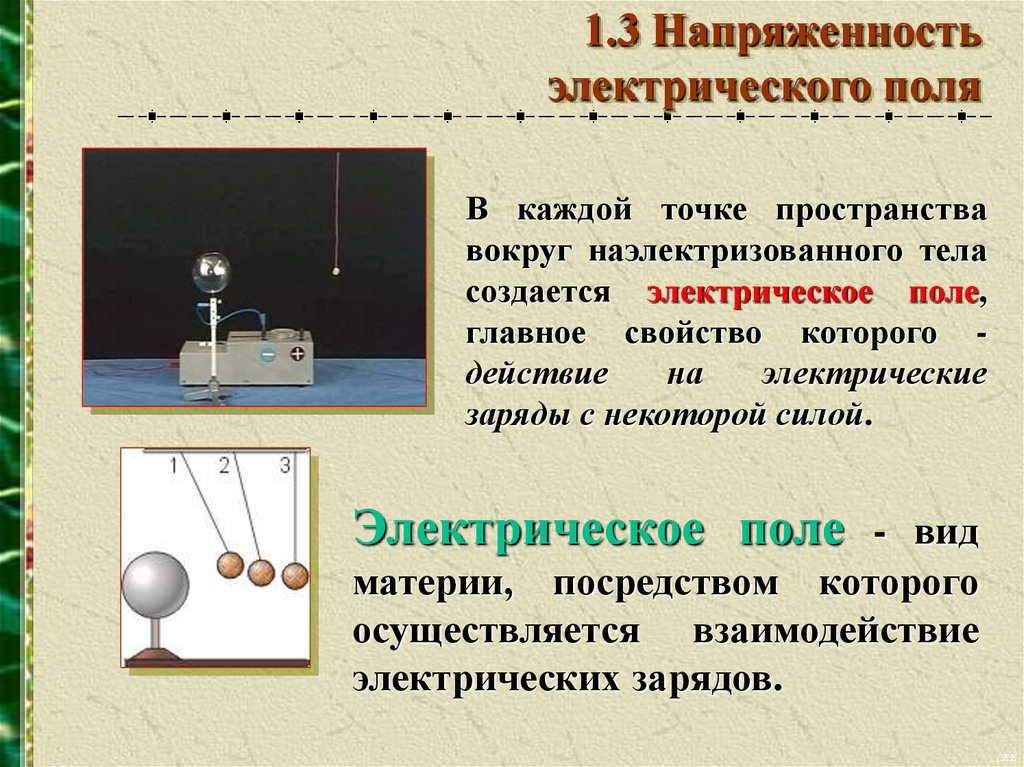
В каждой точке пространства
вокруг наэлектризованного тела
создается электрическое поле,
главное свойство которого действие
на
электрические
заряды с некоторой силой.
Электрическое поле
- вид
материи, посредством которого
осуществляется взаимодействие
электрических зарядов.
CEE
19.
1.3 Напряженностьэлектрического поля
«Электрическое поле
также реально, как и
стул, на котором мы
сидим».
А. Эйнштейн
CEE
20.
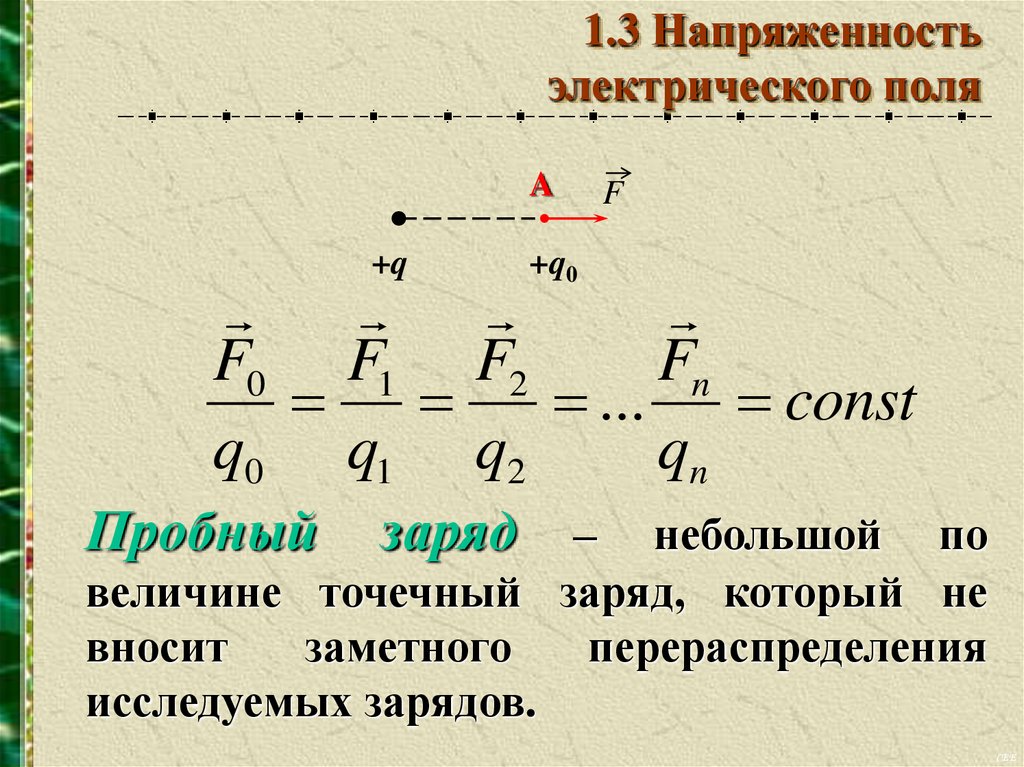
1.3 Напряженностьэлектрического поля
A
+q
F
+q0
F0 F1 F2
Fn
... const
q0 q1 q2
qn
Пробный
заряд – небольшой по
величине точечный заряд, который не
вносит
заметного
перераспределения
исследуемых зарядов.
CEE
21.
1.3 Напряженностьэлектрического поля
!
Напряженностью
электрического поля
называют физическую величину, равную
отношению силы, с которой поле действует
на
положительный
пробный
заряд,
помещенный в данную точку пространства,
к величине этого заряда:
F
E .
q0
Напряженность – силовая
электрического поля.
характеристика
CEE
22.
1.3 Напряженностьэлектрического поля
Если q0 = 1Кл, то
!
E
численно равна
F.
Напряженность электрического поля в
данной точке есть физическая величина,
численно равная силе, с которой поле
.
действует на единичный положительный
заряд, помещенный в данную точку поля.
Н B
Е .
Кл м
CEE
23.
1.3 Напряженностьэлектрического поля
Напряженность поля точечного заряда
F
E
q0
F
1 q r
E
2
4π 0 r r
1 qq0 r
2
4 0 r r
.
1 q
E
2
4π 0 r
r
здесь
− радиус-вектор, проведенный от заряда q в
рассматриваемую точку поля.
CEE
24.
1.3 Напряженностьэлектрического поля
Напряженность поля точечного заряда
q0
q
!
для вакуума
1 q
E
2
4π 0 r
для среды
1 q
E
2
4π 0 r
Численное
значение
напряженности
поля
точечного заряда будет одинаковым во всех точках
поля, которые одинаково удалены от заряда q.
Иначе говоря, напряженность поля будет одинакова
во всех точках сферы, в центре которой
расположен заряд.
CEE
25.
1.3 Напряженностьэлектрического поля
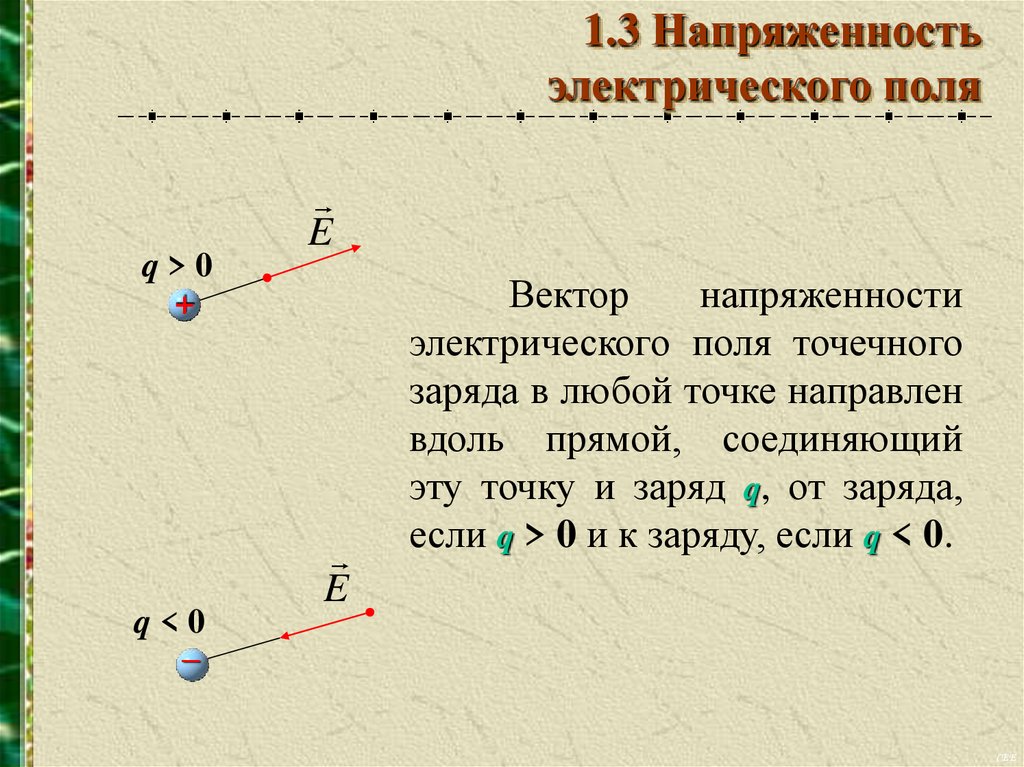
q>0
+
q<0
–
E
E
Вектор
напряженности
электрического поля точечного
заряда в любой точке направлен
вдоль прямой, соединяющий
эту точку и заряд q, от заряда,
если q > 0 и к заряду, если q < 0.
CEE
26.
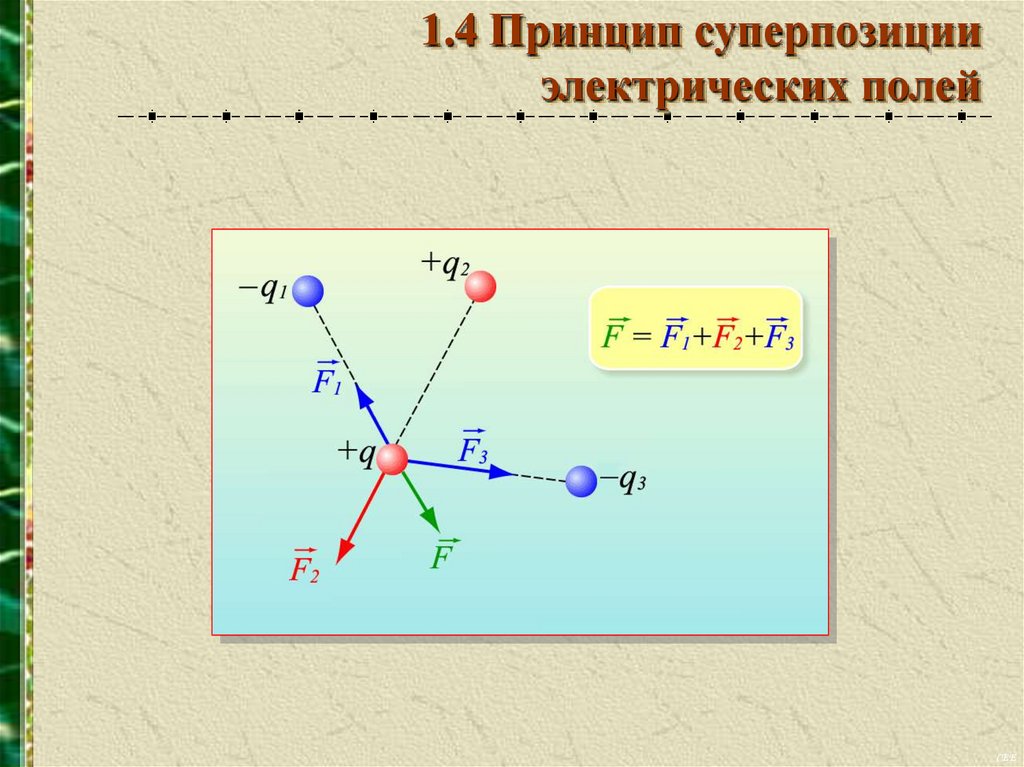
1.4 Принцип суперпозицииэлектрических полей
q0
q1
q3
F F1 F2 ...Fn
q q
F q0 E F1 q0 E1; F2 q0 E2 ,...Fn q0 En
2
n
E E1 E2 ...En
!
n
E Ei
i 1
Напряженность электрического поля, создаваемого
системой зарядов в данной точке пространства, равна
геометрической сумме напряженностей электрических
полей, создаваемых в той же точке каждым зарядом в
отдельности.
CEE
27.
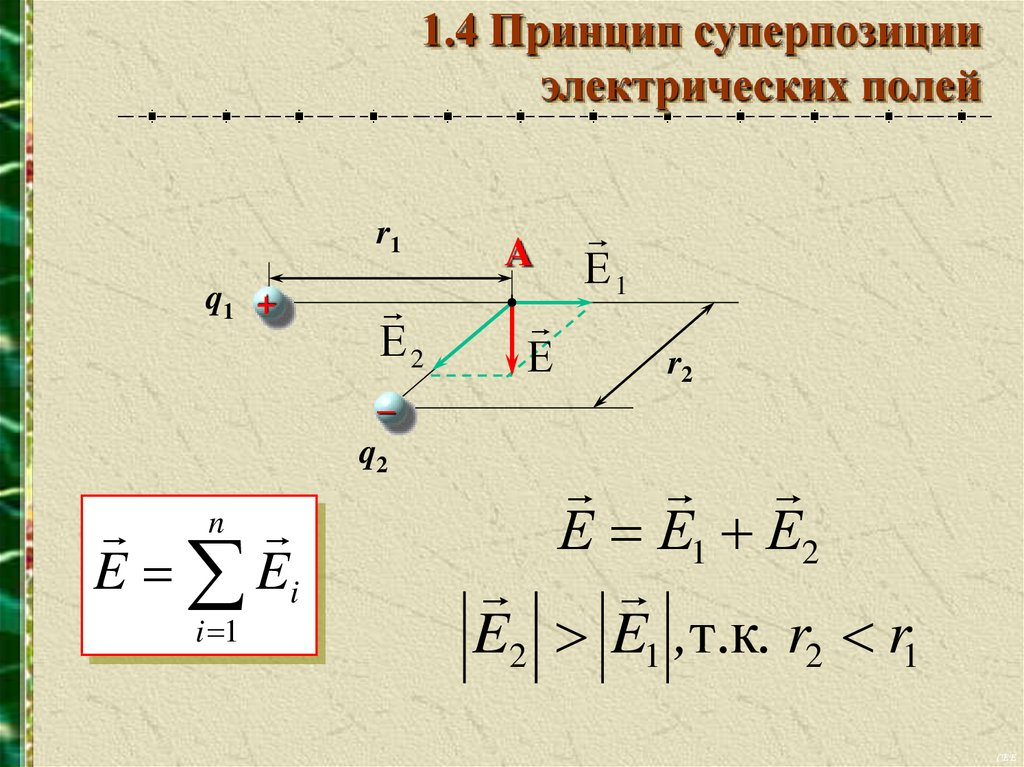
1.4 Принцип суперпозицииэлектрических полей
r1
q1 +
Е2
A
Е
Е1
r2
–
q2
n
E Ei
i 1
Е Е1 Е2
E2 E1 ,т.к. r2 r1
CEE
28.
1.4 Принцип суперпозицииэлектрических полей
CEE
29.
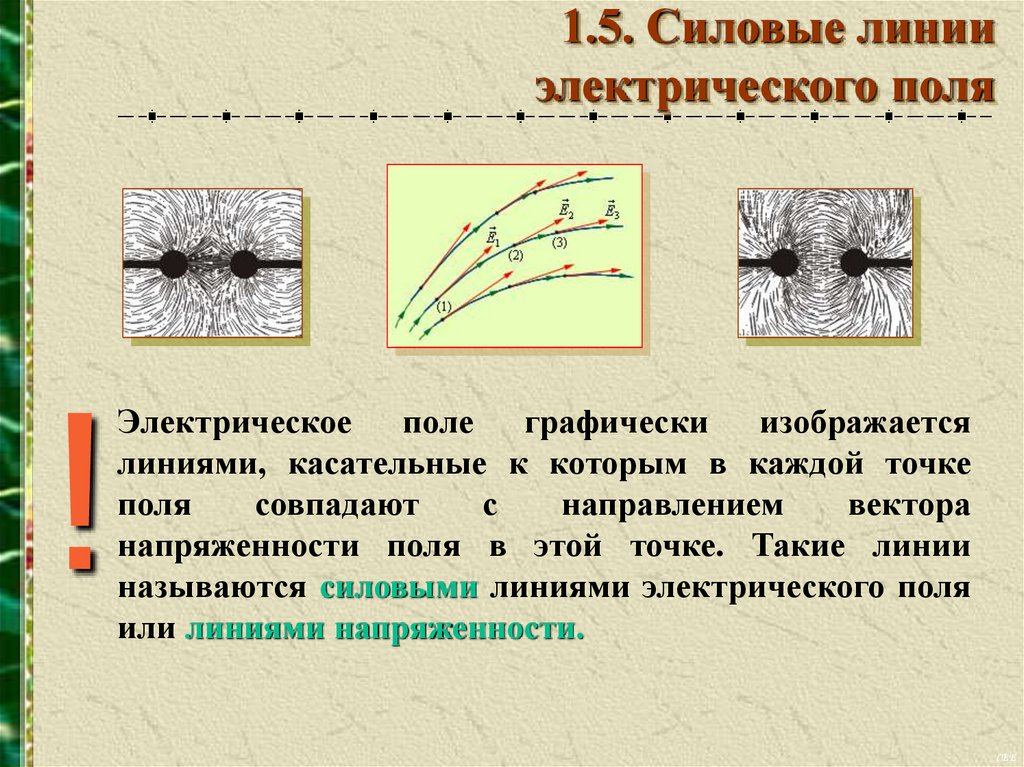
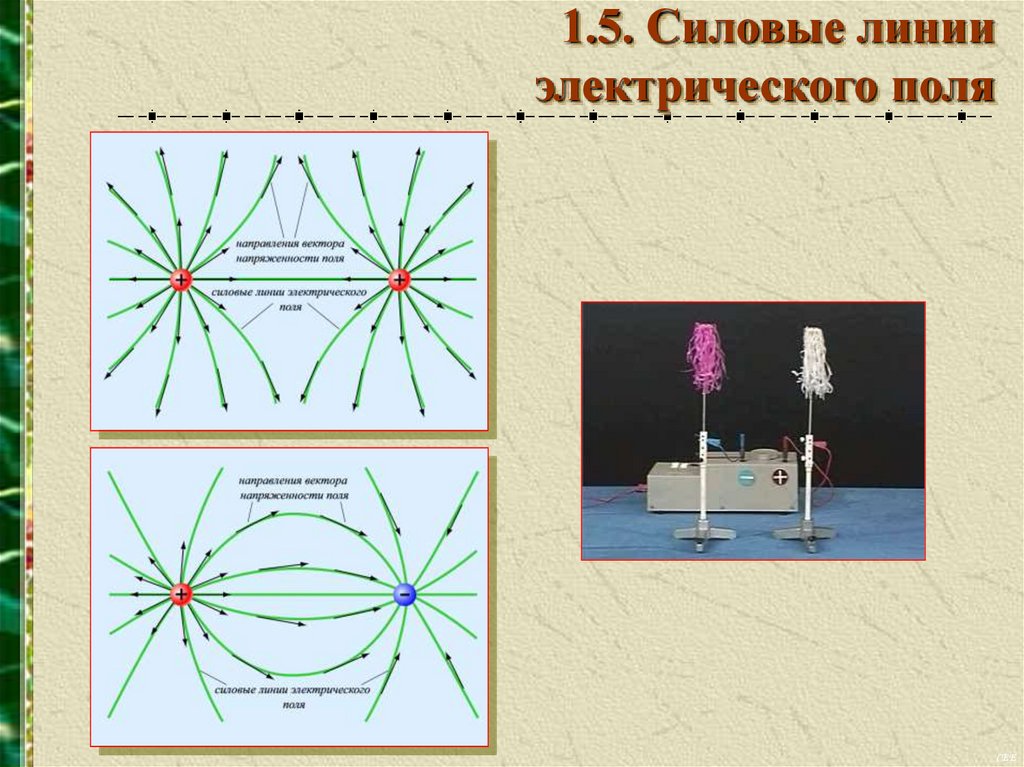
1.5. Силовые линииэлектрического поля
!
Электрическое поле графически изображается
линиями, касательные к которым в каждой точке
поля
совпадают
с
направлением
вектора
напряженности поля в этой точке. Такие линии
называются силовыми линиями электрического поля
или линиями напряженности.
CEE
30.
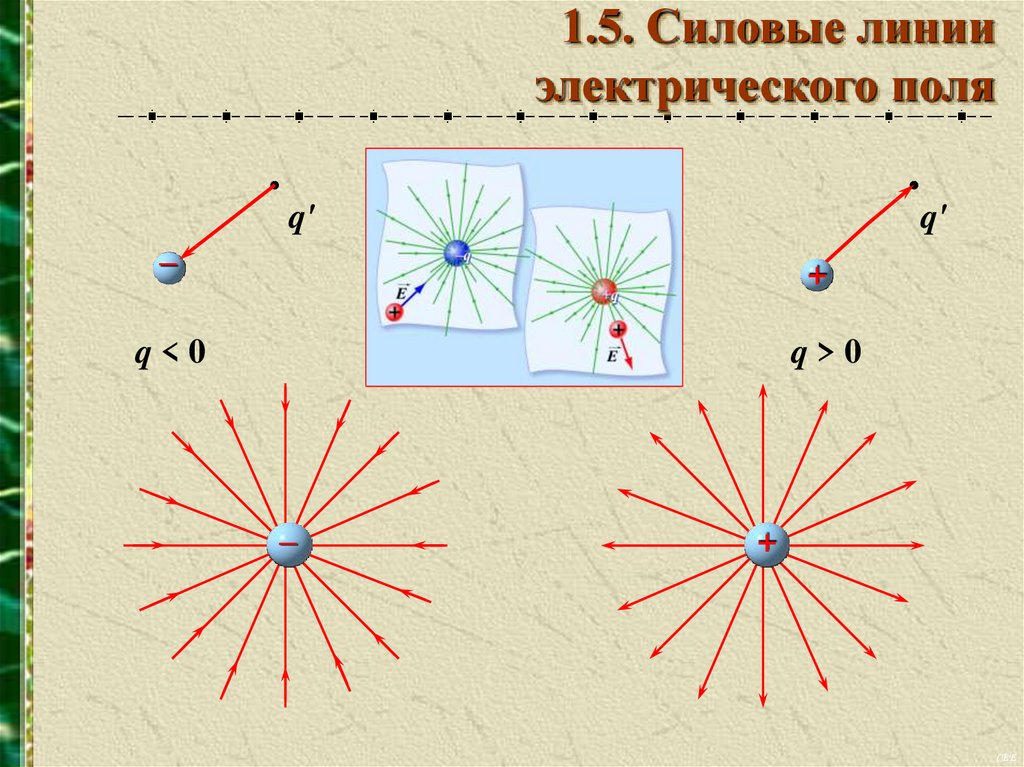
1.5. Силовые линииэлектрического поля
q'
q'
–
+
q<0
q>0
–
+
CEE
31.
1.5. Силовые линииэлектрического поля
CEE
32.
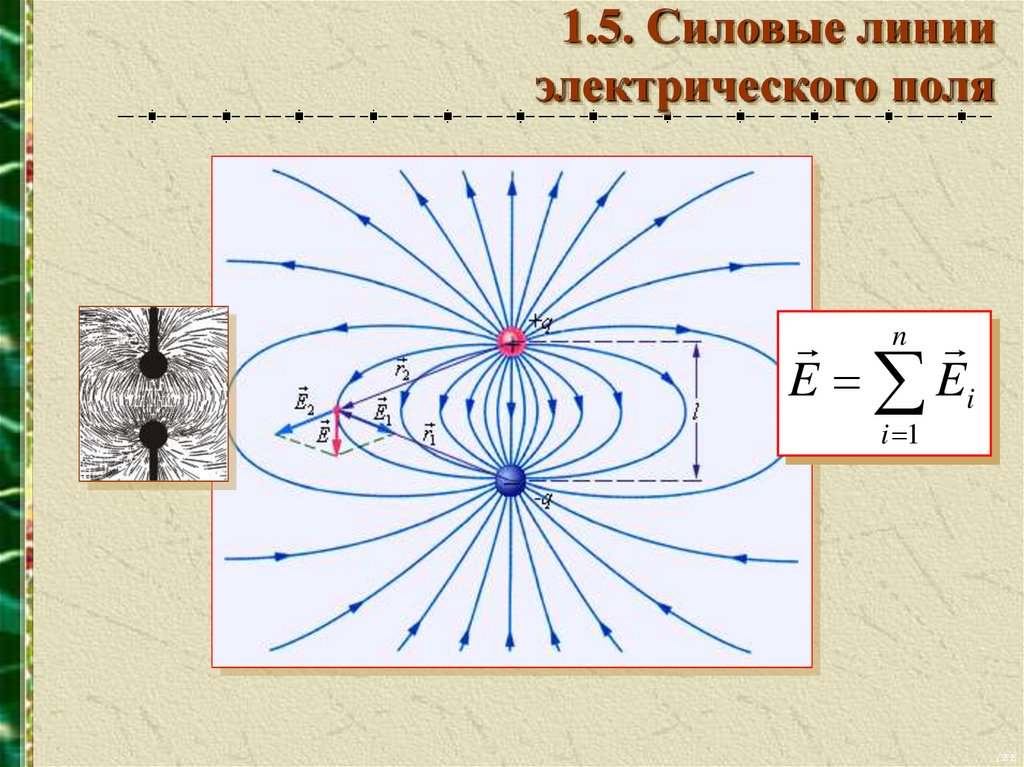
1.5. Силовые линииэлектрического поля
n
E Ei
i 1
CEE
33.
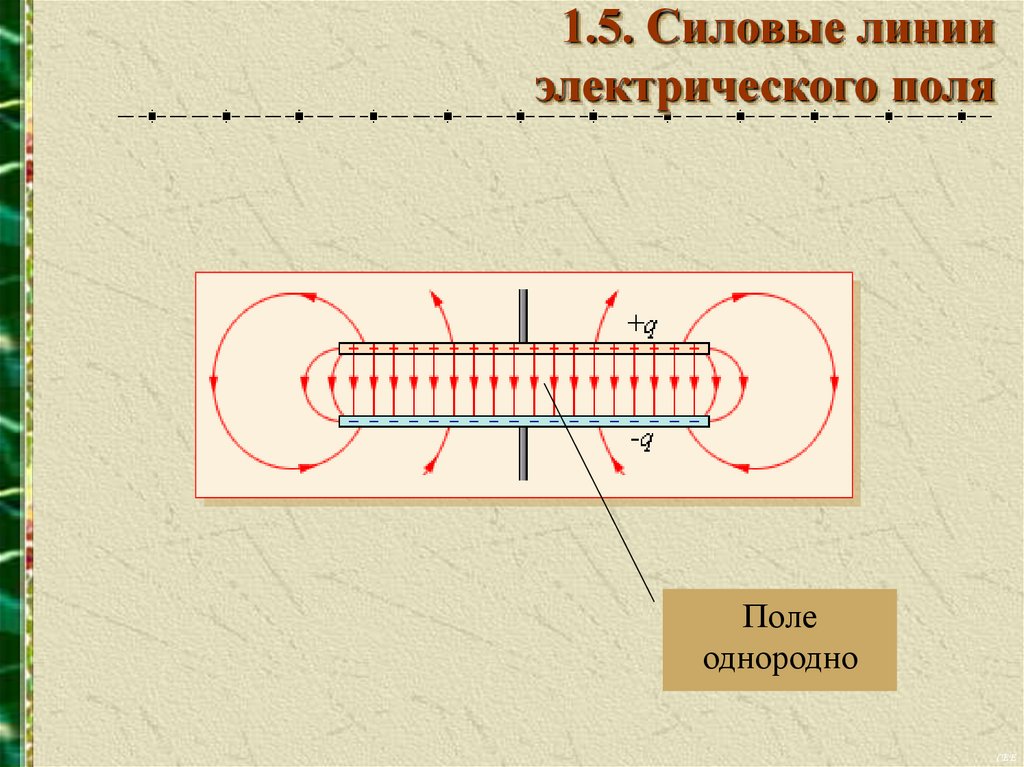
1.5. Силовые линииэлектрического поля
Поле
однородно
CEE
34.
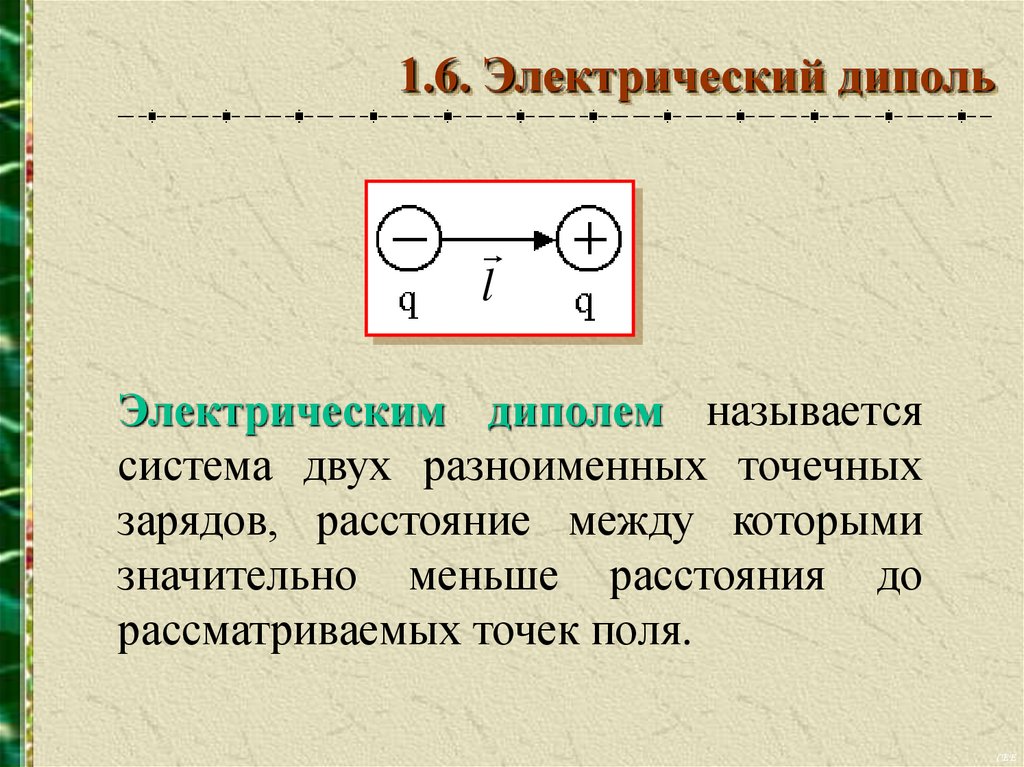
1.6. Электрический дипольl
Электрическим диполем называется
система двух разноименных точечных
зарядов, расстояние между которыми
значительно меньше расстояния до
рассматриваемых точек поля.
CEE
35.
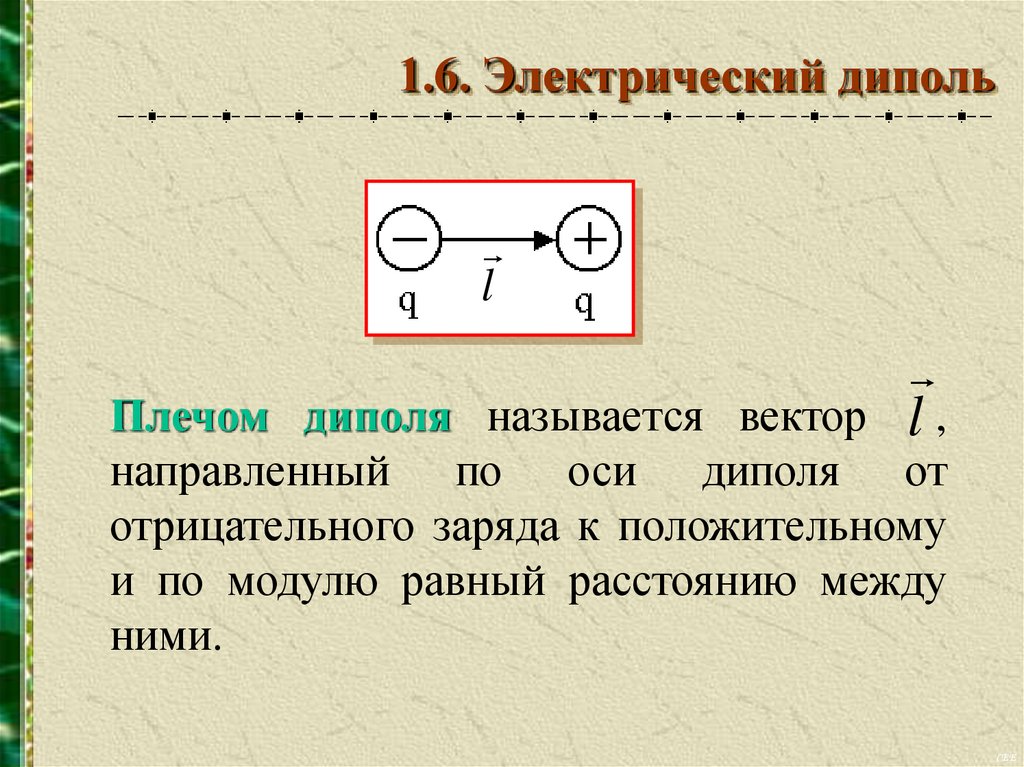
1.6. Электрический дипольl
l,
Плечом диполя называется вектор
направленный по оси диполя от
отрицательного заряда к положительному
и по модулю равный расстоянию между
ними.
CEE
36.
1.6. Электрический дипольЭлектрический диполь
характеризуется
моментом диполя
p ql
В соответствии с принципом суперпозиции
напряженность в произвольной точке поля
диполя:
E E E
CEE
37.
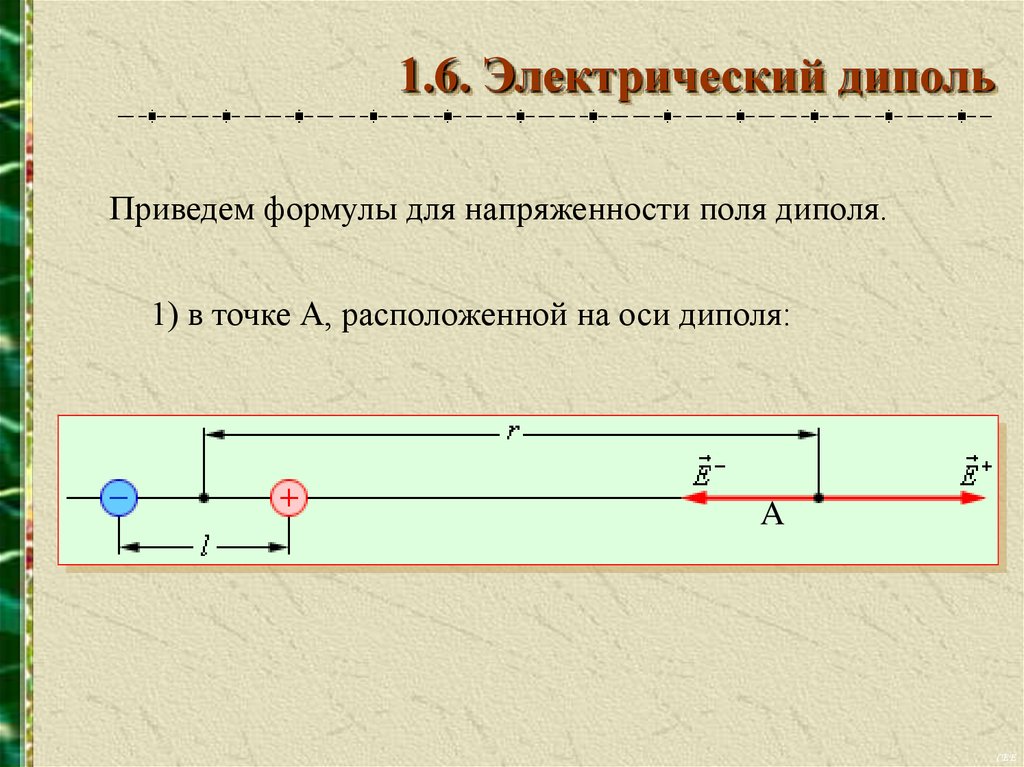
1.6. Электрический дипольПриведем формулы для напряженности поля диполя.
1) в точке А, расположенной на оси диполя:
A
CEE
38.
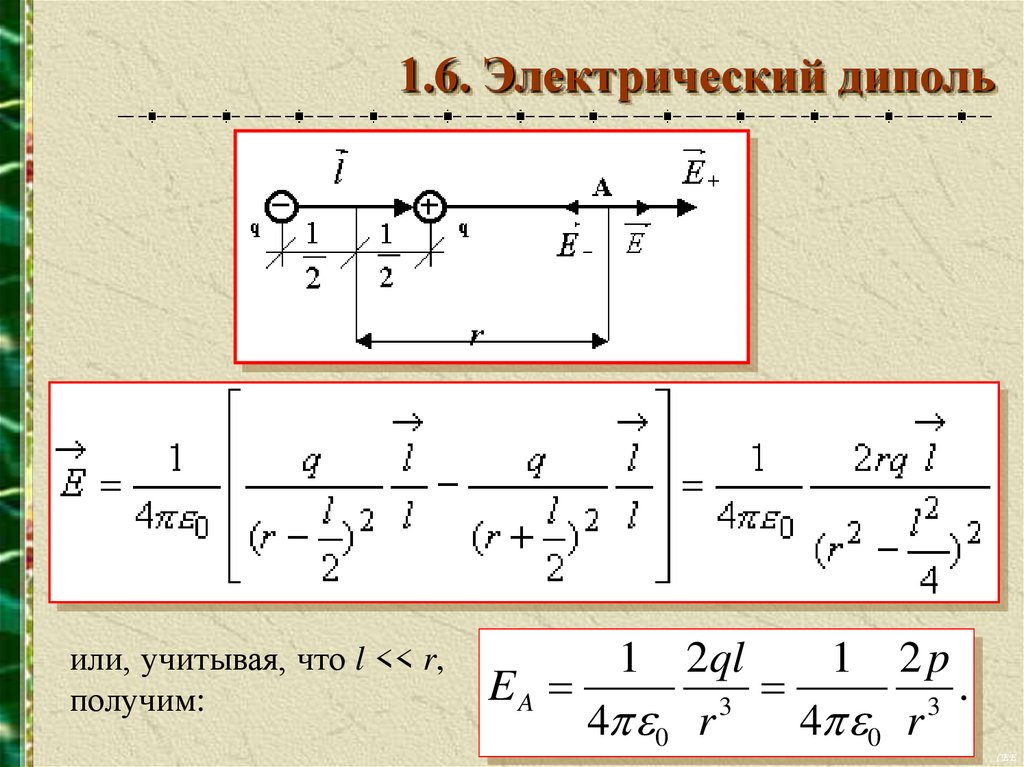
1.6. Электрический дипольили, учитывая, что l << r,
получим:
1
2ql
1 2p
EA
.
3
3
4 0 r
4 0 r
CEE
39.
1.6. Электрический дипольq
или
l
q
На диполь, помещенный
в электрическое поле,
действует момент сил
M qEl sin
Потенциальная энергия
диполя
во
внешнем
электростатическом поле
M pE
который стремится
установить диполь по
полю.
WП pE
CEE




















 physics
physics








