Электрический заряд. Закон Кулона

1.

Лекция 1
Содержание
Электрический заряд
Закон Кулона
Электростатическое поле
Напряжённость поля. Линии напряженности
Работа сил электростатического поля
Потенциал. Эквипотенциальные поверхности
Связь между напряженностью электрического поля и
потенциалом
• Энергия взаимодействия зарядов
• Поток напряженности электрического поля
• Теорема Гаусса для электростатического поля

2.

Электрический заряд частицы является одной из
основных, первичных ее характеристик. Ему присущи
следующие фундаментальные свойства:
1) электрический заряд существует в двух видах: как
положительный, так и отрицательный;
2) в любой электрически изолированной системе алгебраическая
сумма зарядов не изменяется, это утверждение выражает
закон сохранения электрического заряда;
3) электрический заряд является релятивистски-инвариантным:
его величина не зависит от системы отсчета, а значит, не
зависит от того, движется он или покоится.
4) все заряды в природе кратны заряду электрона: q N e , где N
- целое.

3.

Точечным зарядом является заряженное тело, геометрическими
размерами которого в данных условиях можно пренебречь.
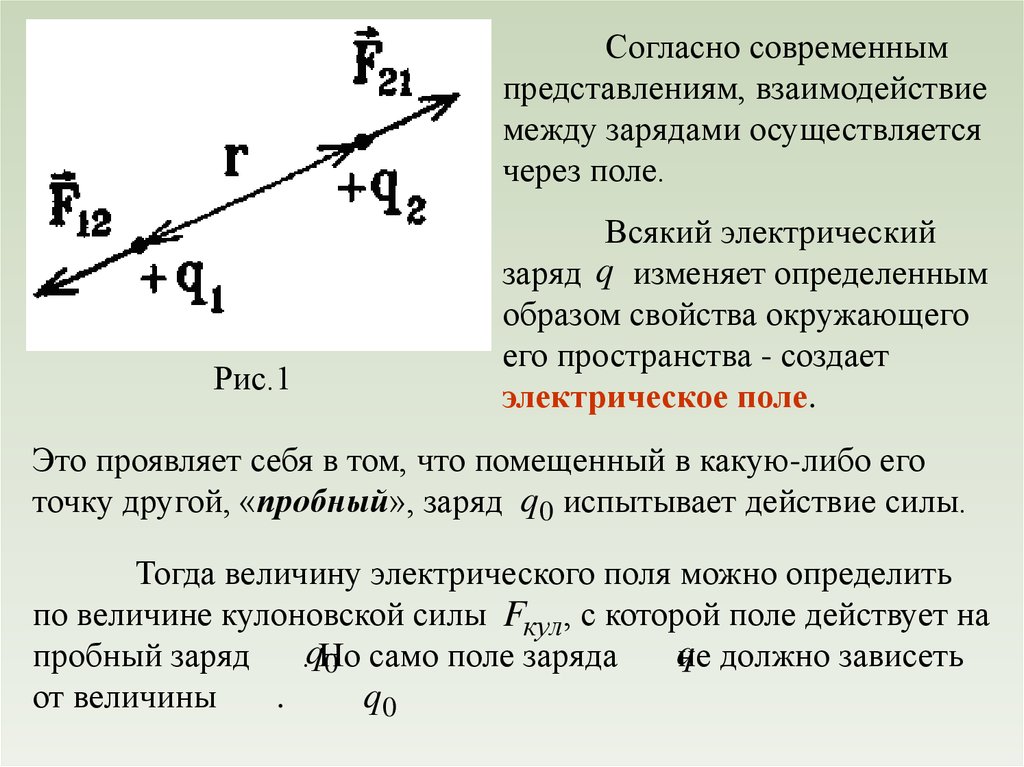
Закон Кулона (1785 г.) устанавливает, что сила взаимодействия
двух точечных электрических зарядов q1 и q2 , находящихся в
вакууме на расстоянии r друг от друга (рис.1), определяется
выражением:
q1q2
F12 k 2 er ,
r
(1.1)
e
где r - это орт радиус-вектора, направленный вдоль линии,
1
соединяющей точечные заряды, k
9 109 м Ф ,
4 0
12
Ф м называется электрической
постоянная 0 8,85 10
постоянной. Заряд q выражается в кулонах [ Кл].

4.

Согласно современным
представлениям, взаимодействие
между зарядами осуществляется
через поле.
Рис.1
Всякий электрический
заряд q изменяет определенным
образом свойства окружающего
его пространства - создает
электрическое поле.
Это проявляет себя в том, что помещенный в какую-либо его
точку другой, «пробный», заряд q0 испытывает действие силы.
Тогда величину электрического поля можно определить
по величине кулоновской силы Fкул , с которой поле действует на
qне должно зависеть
пробный заряд
.qНо
0 само поле заряда
q0
от величины
.

5.

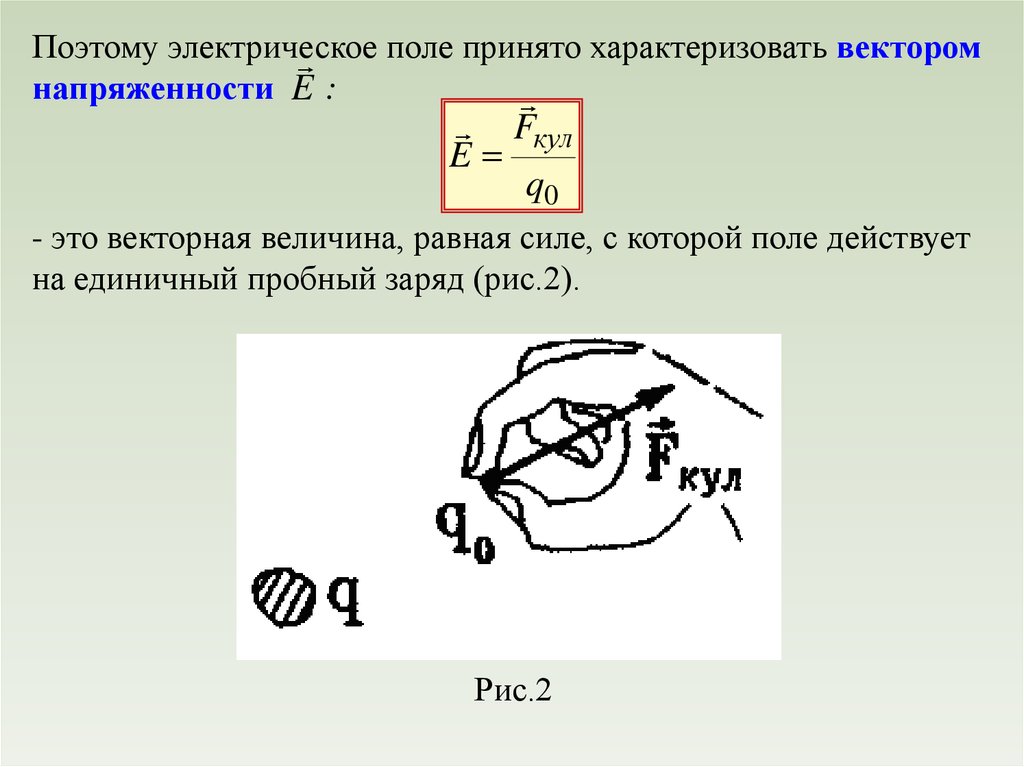
Поэтому электрическое
поле принято характеризовать вектором
напряженности E :
Fкул
E
q0
- это векторная величина, равная силе, с которой поле действует
на единичный пробный заряд (рис.2).
Рис.2

6.

Тогда напряженность поля неподвижного точечного заряда q на
расстоянии
от
r него можно представить как
1 q
E
er .
2
4 0 r
(1.2)
Напряженность поля E выражается в вольтах на метр (В/м).
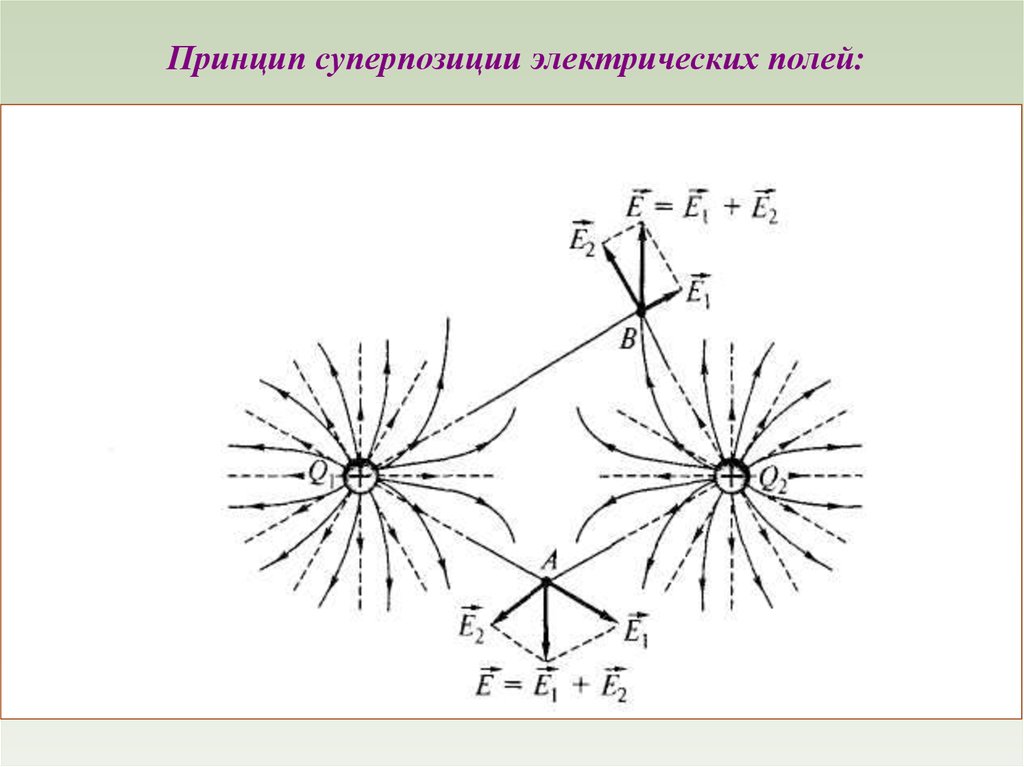
Принцип суперпозиции. Напряженность поля системы
точечных неподвижных зарядов равна векторной сумме
напряженностей полей, которые создавали бы каждый из зарядов
в отдельности:
N
E Ei
i 1
N
qi
2 eri ,
4 0 i 1ri
1
где ri расстояние между зарядом qi , и интересующей нас
точкой поля.
(1.3)

7.

Принцип суперпозиции электрических полей:

8.

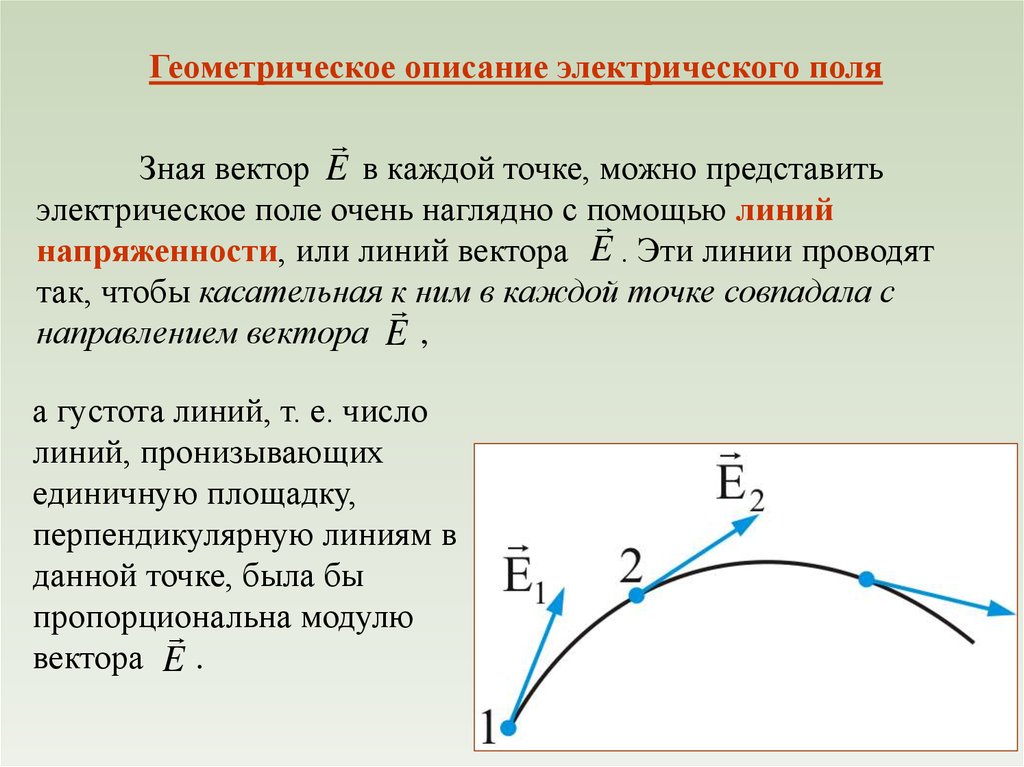
Геометрическое описание электрического поля
Зная вектор E в каждой точке, можно представить
электрическое поле очень наглядно с помощью
линий
напряженности, или линий вектора E . Эти линии проводят
так, чтобы касательная к ним в каждой точке совпадала с
направлением вектора E ,
а густота линий, т. е. число
линий, пронизывающих
единичную площадку,
перпендикулярную линиям в
данной точке, была бы
пропорциональна
модулю
вектора E .

9.

10.

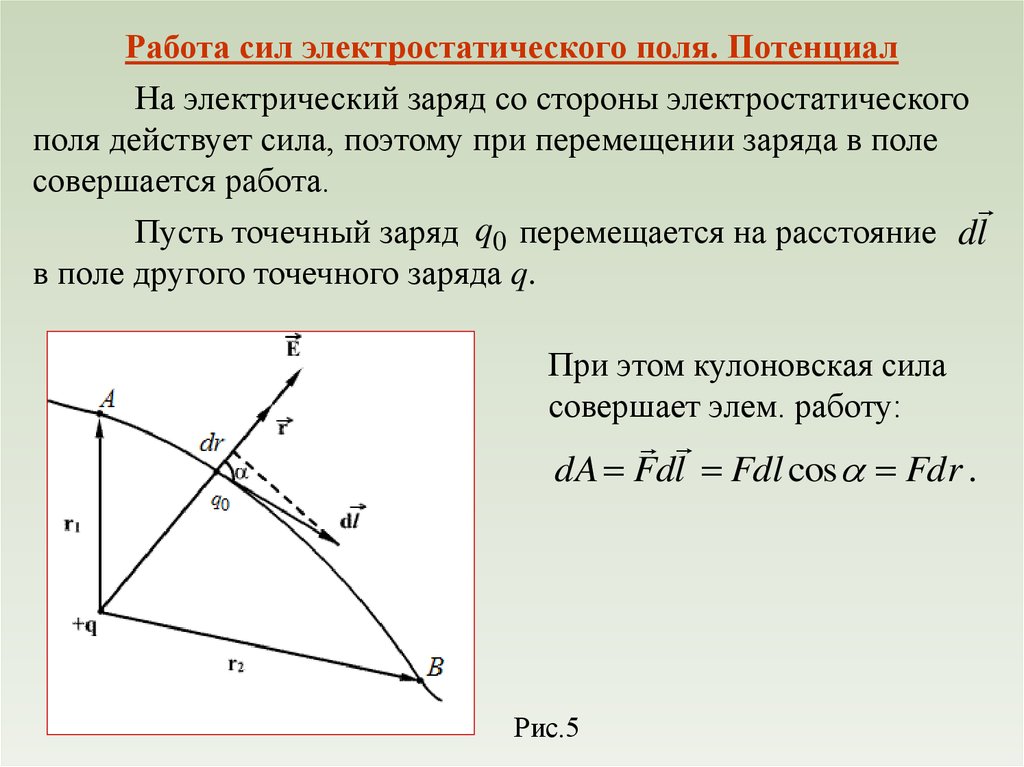
Работа сил электростатического поля. Потенциал
На электрический заряд со стороны электростатического
поля действует сила, поэтому при перемещении заряда в поле
совершается работа.
Пусть точечный заряд q0 перемещается на расстояние dl
в поле другого точечного заряда q.
При этом кулоновская сила
совершает элем. работу:
dA Fdl Fdl cos Fdr .
Рис.5

11.

Полная работа:
qq0 dr qq0 1 1
A12 dA
.
2
4 0 r1 r2
r
r 4 0 r
r2
r2
1
1
Вывод: Работа по перемещению заряда в эл. поле не зависит от
формы пути, т.е. электростатические силы являются
потенциальными или консервативными.
По определению консервативности силы эта работа идет
на изменение потенциальной энергии W взаимодействия
зарядов:
dA dW или A12 W2 W1 ,
отсюда следует, что кулоновская потенциальная энергия
взаимодействия двух точечных зарядов, находящихся на
расстоянии r друг от друга, равна:

12.

1 qq0
W
.
4 0 r
Разделив это выражение на величину пробного заряда q0 ,
получаем выражение для потенциала поля точечного заряда q ,
находящегося в начале координат:
W
1 q
,
q0 4 0 r
т.е. потенциал равен потенциальной энергии единичного
точечного заряда в данной точке поля. Единицей измерения
потенциала является Вольт [В].
И потенциал, и потенциальная энергия определены с
точностью до произвольной постоянной. Эта постоянная
выбирается так, чтобы на бесконечном удалении r W
и были равны нулю.

13.

Поэтому можно сказать, что потенциалом электрического
поля называется работа по перемещению единичного
положительного заряда из данной точки поля в
бесконечность:
A1
q0
Для потенциала также, как и для напряженности, справедлив
принцип суперпозиции: потенциал системы зарядов равен
алгебраической сумме потенциалов отдельных зарядов:
1 N qi
.
4 0 i 1 ri
Потенциал поля непрерывно
распределенного заряда (рис.6 ):
Рис.6
1
dV
.
4 0 V r

14.

Связь между вектором E и для электрического поля
Элементарная работа dA электрического поля:
dA Fdl q0 Edl .
Тогда работа электрического поля по переносу пробного заряда
из точки 1 в точку 2 :
A12 q0 Edl .
2
1
Т.к. электростатическое поле потенциально, то эта работа равна
разности потенц. энергий пробного заряда в этом эл. поле:
A12 W2 W1 q0 1 2 .
Получаем связь разности потенциалов и напряженности эл. поля:
1 2 Edl .
2
1

15.

Теперь получим обратное соотношение. Для этого
запишем полученное соотношение в дифференциальной форме:
d Edl Ex dx E y dy Ez dz .
Для того чтобы из этой формулы определить проекцию
напряженности эл. поля, например, по оси x, необходимо
считать остальные переменные постоянными величинами.
В математике такая производная называется частной:
Ex
,
x
E y , Ez .
z
y
Эти три производные объединяют в векторный оператор,
который носит название градиент (или оператор ).
Запишем окончательную формулу:
E grad i
j
k
.
y
z
x

16.

Эквипотенциальные поверхности
Введем понятие эквипотенциальной поверхности —
поверхности, во всех точках которой потенциал имеет одно и
то же значение.
Эквипотенциальные поверхности проводят так, чтобы
разность потенциалов между двумя соседними поверхностями
была одна и та же. Там, где потенциал поля больше,
эквипотенциальные поверхности расположены гуще.
Вектор E направлен в каждой точке по нормали к
эквипотенциальной поверхности в сторону уменьшения
потенциала .
Для сложной системы зарядов проще вычислить
потенциал, поскольку он является скалярной величиной, а затем,
по известному распределению потенциала
всегда можно
определить напряженность поля, как: E grad .

17.

18.

Энергия взаимодействия системы электрических зарядов
Потенциальная энергия двух зарядов q1 и q2 может быть
представлена в форме:
W p12
q1 q2
.
4 o r12
1
Энергия системы из N зарядов (q1, q2, …qN) определяется как
сумма энергий взаимодействия зарядов, взятых попарно:
1
Wp
W pik rik ,
2 (i k )
здесь
W pik
1 qi qk
.
4 o rik
Тогда формула для потенциальной энергии системы зарядов:
1
1
qi qk
Wp
.
2 (i k ) 4 o rik
Здесь все индексы i и k пробегают значения от 1 до N, значения i
= k не принимаются во внимание.

19.

Это выражение можно переписать в виде:
N
1N
1
qk
W p qi
,
2 i 1 k 1( k i ) 4 o rik
1
N
qk
величина i
4 o k 1( k i ) rik
есть потенциал, создаваемый всеми зарядами, кроме qi, в точке,
где помещен заряд qi.
Выражение для потенциальной энергии системы электрических
зарядов можно записать также в виде:
1N
W p qi i .
2 i 1

20.

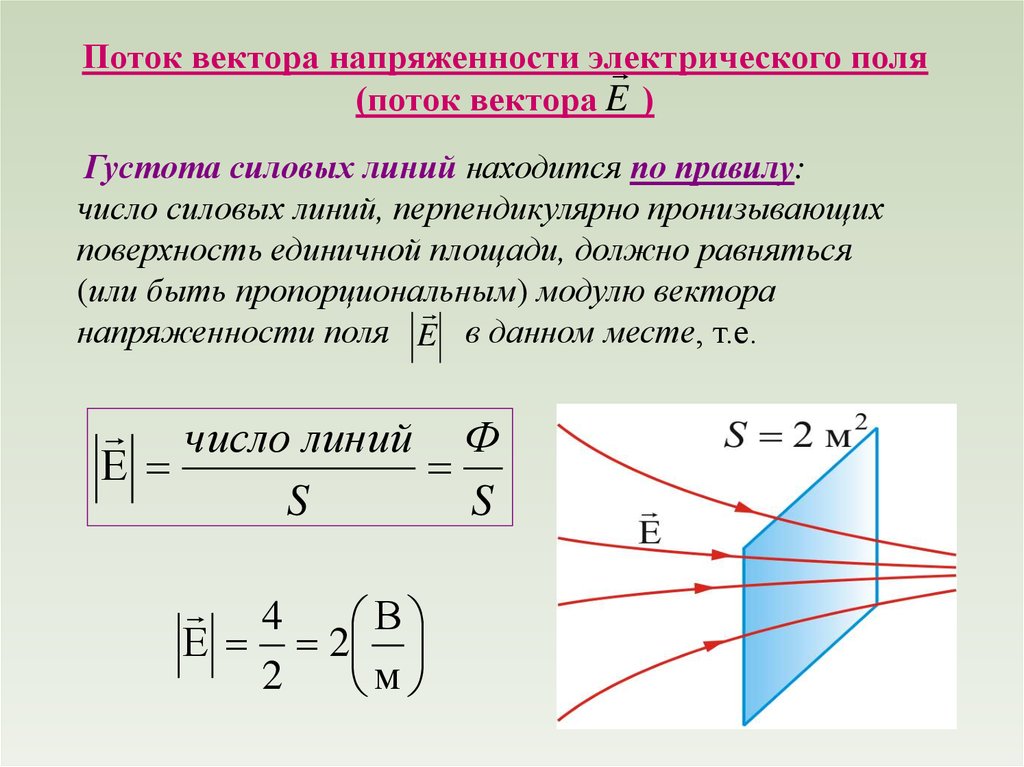
Поток вектора напряженности электрического
поля
(поток вектора E )
Густота силовых линий находится по правилу:
число силовых линий, перпендикулярно пронизывающих
поверхность единичной площади, должно равняться
(или быть пропорциональным)
модулю вектора
напряженности поля E в данном месте, т.е.
число линий Ф
Е
S
S
4
В
Е 2
2
м

21.

Полное число силовых линий, проходящих через поверхность S
называется потоком вектора напряженности ФЕ через эту
поверхность.
• Поток вектора напряженности через произвольную элемент.
площадку dS будет равен:
dФЕ ЕdS cos En dS .
{Т.О., поток вектора Е есть скаляр, который в зависимости от величины угла α
может быть как > 0, так и < 0.}
• Т.е. в однородном поле:
ФЕ ES.
• В произвольном эл. поле:
ФЕ EdS Еn dS .
S
S

22. Теорема Гаусса и ее применение к расчету электрических полей

Для вычисления напряженности эл. полей, обладающих
симметрией, применяется теорема Гаусса.
Определим поток вектора Е через произвольную
замкнутую поверхность S, окружающую точечный заряд q.

23.

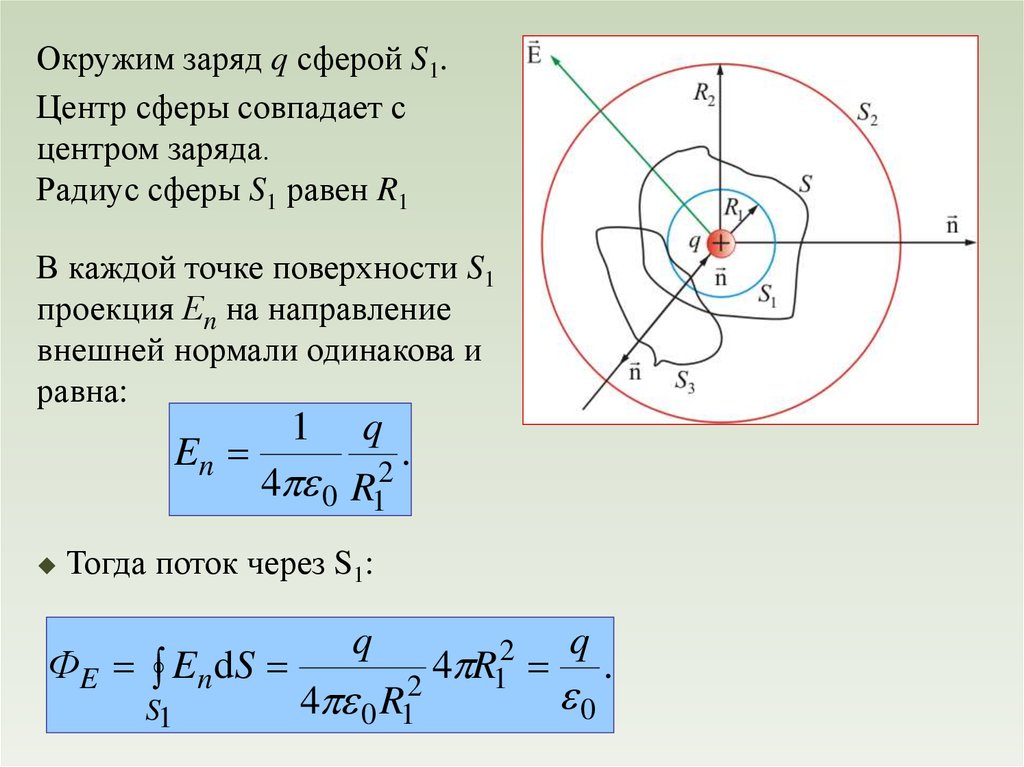
Окружим заряд q сферой S1.
Центр сферы совпадает с
центром заряда.
Радиус сферы S1 равен R1
В каждой точке поверхности S1
проекция Еn на направление
внешней нормали одинакова и
равна:
En
1
q
4 0 R12
.
Тогда поток через S1:
ФE En dS
S1
q
2
4 R1
2
4 0 R1
q
0
.

24.

Поток через сферу S2, имеющую радиус R2:
q
ФЕ
2
S2 4 0 R2
dS
q
2
4 R2
2
4 0R2
q
0
.
Из непрерывности линии Е следует, что поток и через любую
произвольную поверхность S будет равен этой же величине:
ФЕ Еn dS
S
q
0
– теорема Гаусса
для одного заряда.

25.

Для любого числа произвольно расположенных зарядов,
находящихся внутри поверхности:
q
ФЕ Еn dS
0
S
– теорема Гаусса
для системы зарядов
(в интегральной форме).
Поток вектора напряженности электрического поля
через замкнутую поверхность в вакууме равен
алгебраической сумме всех зарядов, расположенных
внутри поверхности, деленной на ε0.

26.

Полный поток проходящий через S3, не охватывающую
заряд q, равен нулю:
Ф3 0.

27.

Суммарный заряд объема dV можно записать:
qi dV .
V
Тогда можно получить:
1
ФE ЕdS dV
ε0 V
S
– это ещё одна форма записи теоремы Гаусса, если
заряд неравномерно распределен по объему.