Similar presentations:
Электрический заряд и его свойства
1.
ФИЗИКА2. Лекция 3
• 1. Электростатическое поле. Закон Кулона• 2. Напряженность и потенциал точечного
заряда . Принцип суперпозиции.
• 3.Постоянный ток. Закон Ома для
однородного и неоднородного участков цепи
3. 1.Электрический заряд и его свойства
• С современной точки зрения,носителями зарядов являются
элементарные частицы.
• Электрический заряд – это
физическая
величина,
характеризующая
свойство
частиц или тел вступать в
электромагнитные
силовые
взаимодействия .
• Единица измерения заряда в СИ —
Кулон. Заряд в 1 Кл очень велик.
4. Свойства электрического заряда
Электрический зарядквантуется (имеет
дискретную природу)
Элементарный зарядзаряд электрона
В природе существуют
два вида зарядовположительные и
отрицательные
Закон сохранения
электрического заряда
Q ne
n 1,2,3...
19
e 1,6 10 Кл
В 1897 г. Дж. Томсоном была открыта и
наименьшая
устойчивая
частица,
являющаяся носителем элементарного
отрицательного заряда.
n
q
i 1
i
const
5. Закон Кулона (1785г.)
Электростатикарассматривает поле,
созданное неподвижными электрическими
зарядами.
• Силы
взаимодействия
неподвижных
зарядов
прямо
пропорциональны
произведению модулей зарядов и обратно
пропорциональны квадрату расстояния
между ними:
2
q1q2
F k 2
r
Нм
k
9 10
4 0
Кл2
1
9
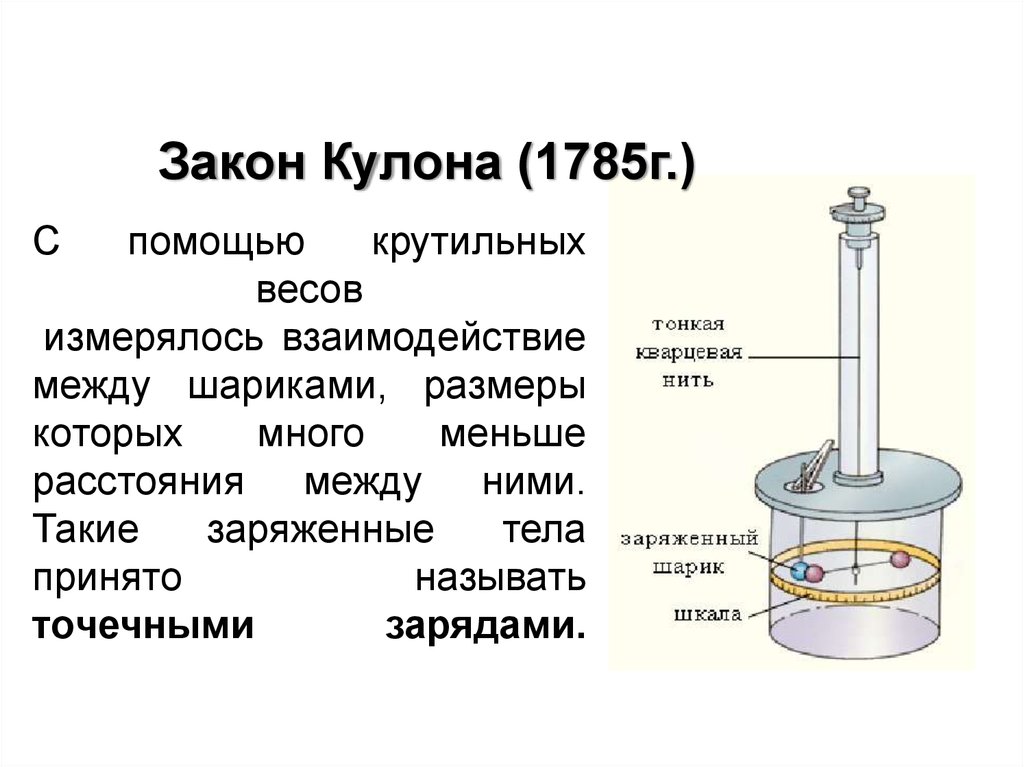
6. С помощью крутильных весов измерялось взаимодействие между шариками, размеры которых много меньше расстояния между ними. Такие
Закон Кулона (1785г.)С
помощью
крутильных
весов
измерялось взаимодействие
между шариками, размеры
которых
много
меньше
расстояния между ними.
Такие
заряженные
тела
принято
называть
точечными
зарядами.
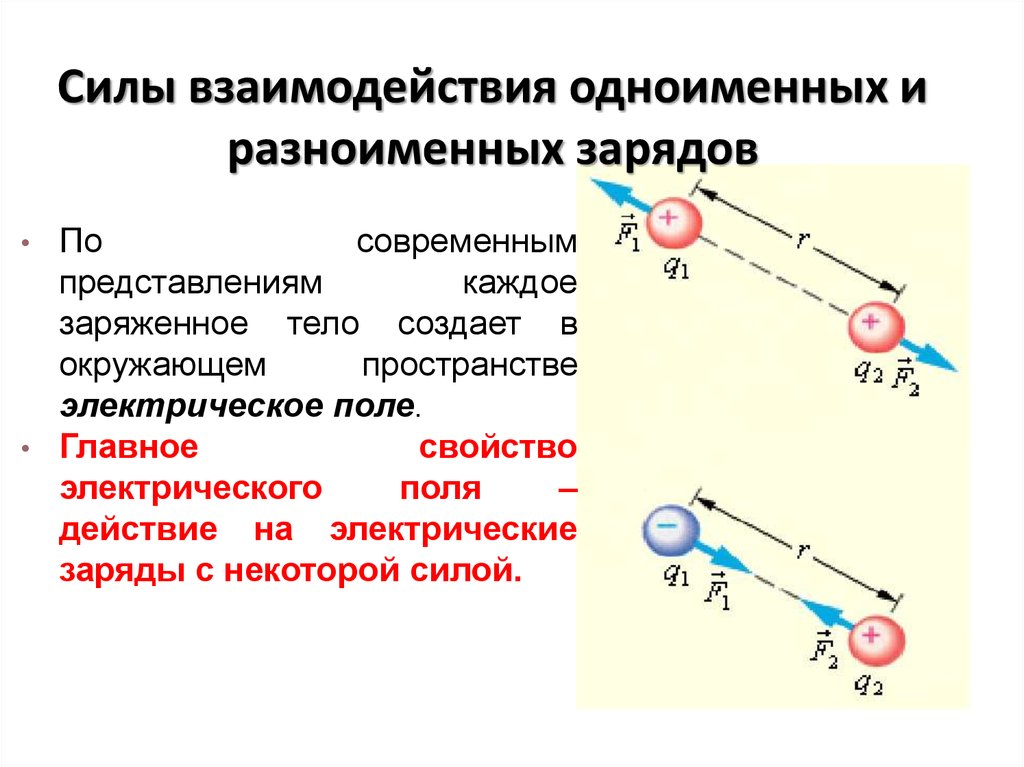
7. Силы взаимодействия одноименных и разноименных зарядов
По
современным
представлениям
каждое
заряженное тело создает в
окружающем
пространстве
электрическое поле.
Главное
свойство
электрического
поля
–
действие на электрические
заряды с некоторой силой.
8. Принцип суперпозиции
Какимбудет
поле,
если оно создается
несколькими зарядами
?
справедлив
ПРИНЦИП СУПЕРПОЗИЦИИ
(наложения полей)
n
F Fi
i 1
9. Напряженность электрического поля
• Напряженностью электрического поля Е называютфизическую величину, равную отношению силы, с
которой поле действует на пробный заряд (точечный,
положительный), помещенный в данную точку
пространства, к величине этого заряда:
F
E
q0
Н В
Е
Кл м
10. Напряженность поля неподвижного точечного заряда Q
Qq0F k 2
r
F
Q
E
k 2
q0
r
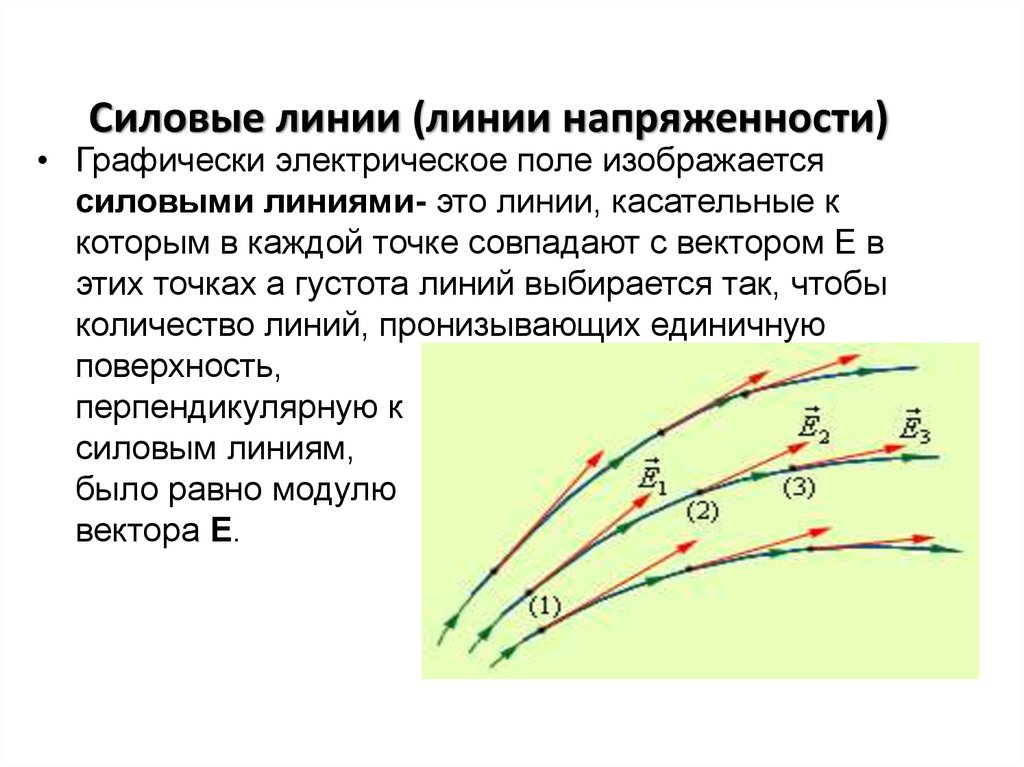
11. Силовые линии (линии напряженности)
• Графически электрическое поле изображаетсясиловыми линиями- это линии, касательные к
которым в каждой точке совпадают с вектором Е в
этих точках а густота линий выбирается так, чтобы
количество линий, пронизывающих единичную
поверхность,
перпендикулярную к
силовым линиям,
было равно модулю
вектора Е.
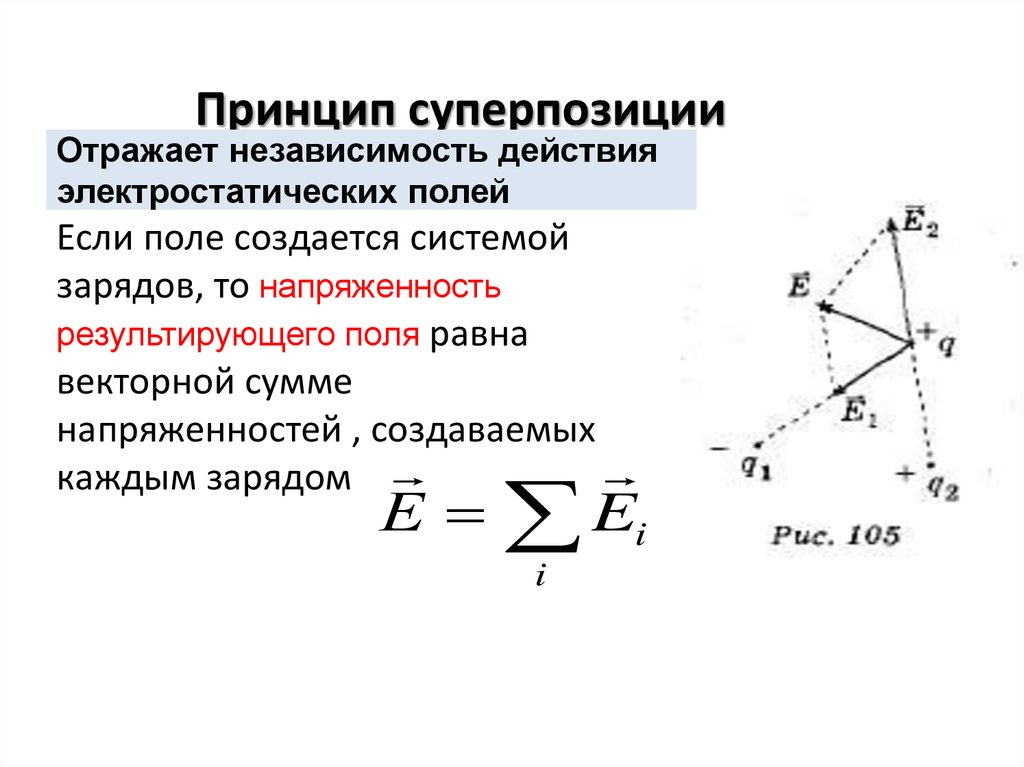
12. Принцип суперпозиции
Отражает независимость действияэлектростатических полей
Если поле создается системой
зарядов, то напряженность
результирующего поля равна
векторной сумме
напряженностей , создаваемых
каждым зарядом
Е Ei
i
13. Потенциальная энергия
• Силы кулоновского взаимодействия являютсяконсервативными, поэтому можно ввести понятие
потенциальной энергии.
dA Fdl q( Edl ) qEdl cos
dl cos dr
kQq0
dA
dr
r2
B
A
dA
C
14. Потенциальная энергия
В поле точечного заряда Q работа поперемещению заряда q0 из точки1 в точку 2:
2
2
kQq0
dr
1 r2
A12 2 dr kQq0 2 kQq0 ( )r
1
r
r
r
1
1
1 1
kQq0 ( ) Wп1 Wп 2
r1 r2
Потенциальная энергия заряда q0 в поле заряда Q
равна
kQq
WП
0
r
15. Потенциал
• Потенциал – это скалярная величина,равная отношению потенциальной энергии,
которой обладает пробный заряд в
электростатическом поле, к величине этого
заряда
Wп
Дж
вольт В
q0
Кл
• Для поля точечного заряда:
Q
k
r
16. Потенциал
Работа сил поля по перемещению заряда q0 из точки 1 вточку 2: A W W
12
П1
П 2 q0 ( 1 2 )
Потенциал численно равен работе сил эл. поля по
перемещению единичного положительного заряда
из данной точки поля на бесконечность.
Принцип суперпозиции:
Потенциал поля , создаваемого системой зарядов, равен
алгебраической сумме потенциалов полей, создаваемых
каждым из зарядов в отдельности.
A q
i
i
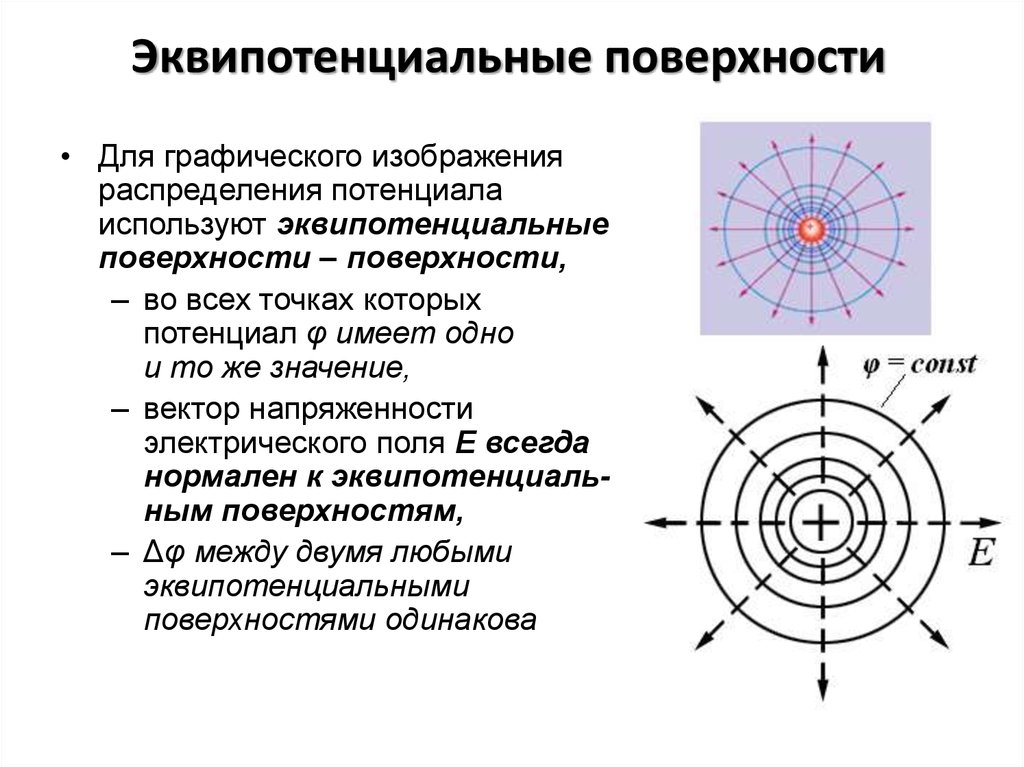
17. Эквипотенциальные поверхности
• Для графического изображенияраспределения потенциала
используют эквипотенциальные
поверхности – поверхности,
– во всех точках которых
потенциал φ имеет одно
и то же значение,
– вектор напряженности
электрического поля Е всегда
нормален к эквипотенциальным поверхностям,
– Δφ между двумя любыми
эквипотенциальными
поверхностями одинакова
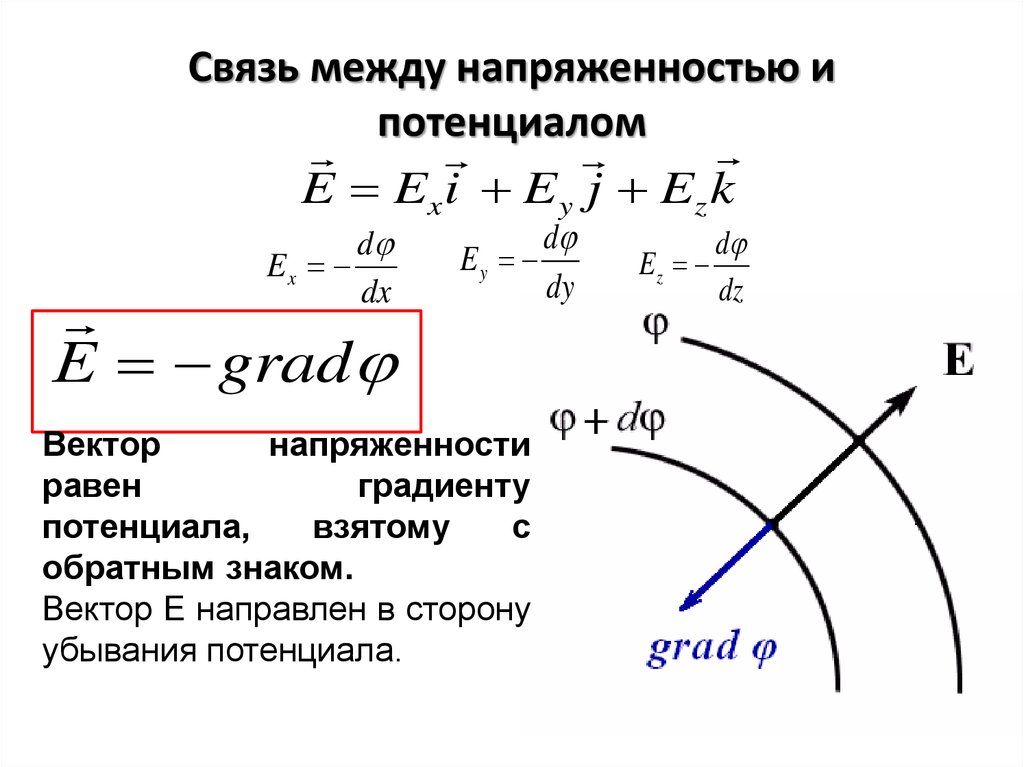
18. Связь между напряженностью и потенциалом
E Ex i E y j Ez kd
Ex
dx
Е grad
d
Ey
dy
Вектор
напряженности
равен
градиенту
потенциала,
взятому
с
обратным знаком.
Вектор Е направлен в сторону
убывания потенциала.
d
Ez
dz
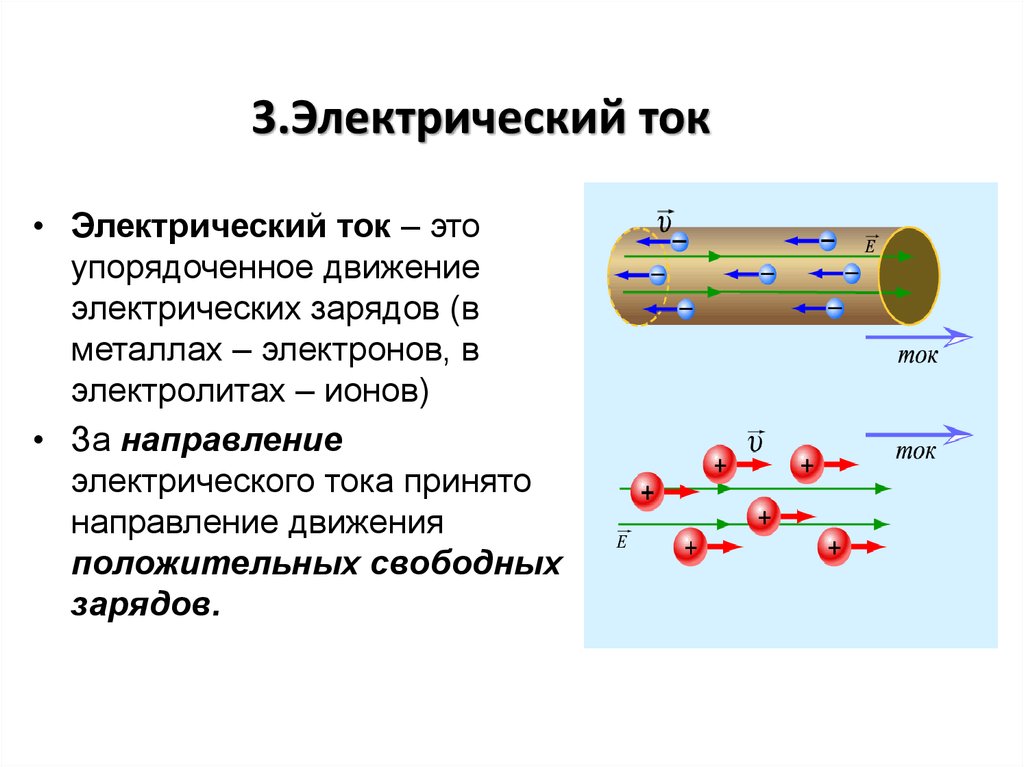
19. 3.Электрический ток
• Электрический ток – этоупорядоченное движение
электрических зарядов (в
металлах – электронов, в
электролитах – ионов)
• За направление
электрического тока принято
направление движения
положительных свободных
зарядов.
20. Сила тока
Сила тока- это количественная характеристика тока:скалярная величина, равная заряду, прошедшему
через поперечное сечение в единицу времени.
dq
I
dt
Если ток не изменяется по величине и направлению,
то он называется постоянным.
q
I
t
21. Измерение силы тока
• Единицы измерения силы тока [I]=Aмпер.• Для измерения силы тока используют амперметр
(миллиамперметр (mA), микроамперметр
(μA),
гальванометр). Его включают в разрыв цепи в том
месте, где нужно измерить силу тока.
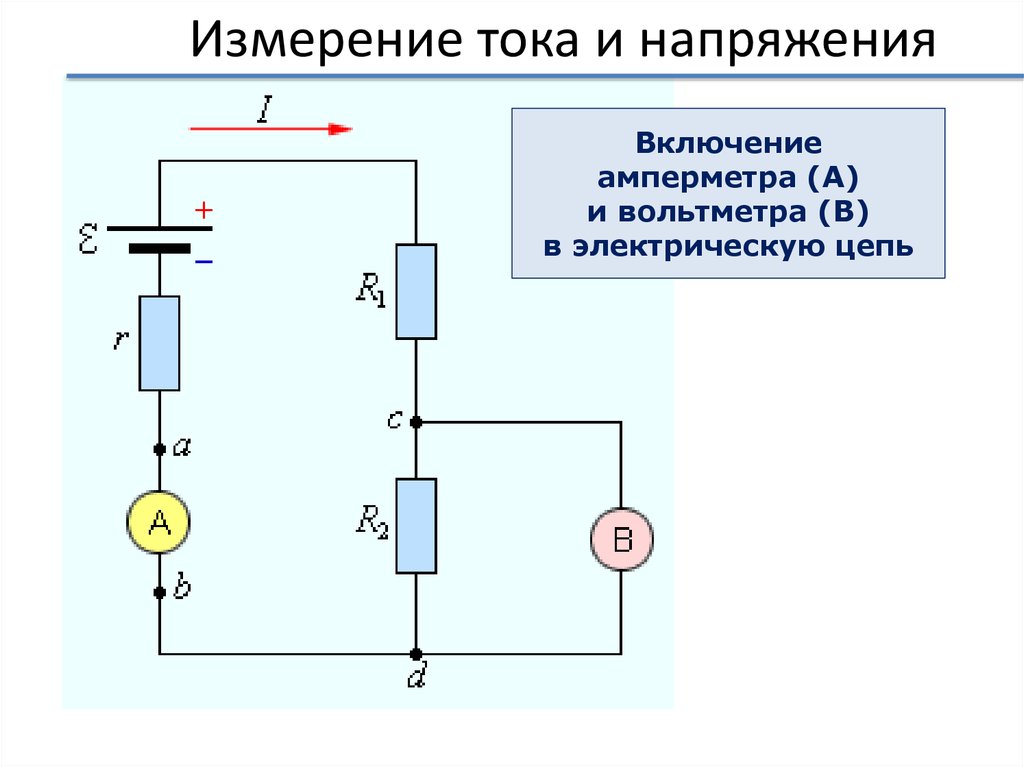
22. Измерение тока и напряжения
Включениеамперметра (А)
и вольтметра (В)
в электрическую цепь
23. Плотность тока
• Плотность тока характеризует распределениеэлектрического заряда по сечению проводника . Это
векторная величина, направление которой совпадает с
направлением скорости упорядоченного движения
положительных зарядов.
v
dI
j
dS
j nq v
dS
nq
24. Электрическая цепь
В замкнутой электрической цепи свободные qциркулируют по замкнутым траекториям
Если на q в цепи действуют
только силы ЭС поля
происходит
перемещение
зарядов q
приводит к
выравнивание
потенциалов
в замкнутой цепи должны быть какие-либо другие силы,
поддерживающие разность потенциалов
Для существования постоянного тока необходимо наличие
в цепи устройства, способного создавать и поддерживать
разность потенциалов за счет работы сил
Источник тока
неэлектростатического происхождения
Силы неэлектростатического происхождения,
действующие на свободные q
Сторонние силы
со стороны источников тока
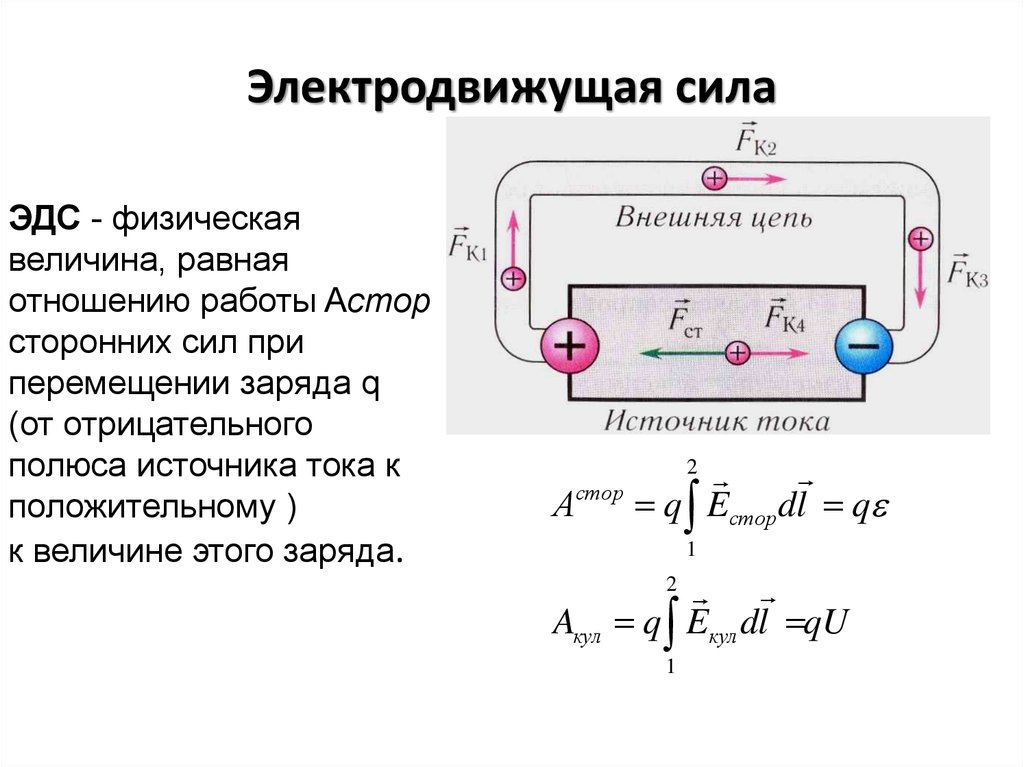
25. Электродвижущая сила
ЭДС - физическаявеличина, равная
отношению работы Aстор
сторонних сил при
перемещении заряда q
(от отрицательного
полюса источника тока к
положительному )
к величине этого заряда.
q Eстор dl q
2
А
стор
1
q Eкул dl qU
2
Aкул
1
26. Закон Ома для однородного участка цепи
• Участки цепи, на которых не действуютсторонние силы (не содержащие источников
тока), называются однородными.
• Участки, включающие источники тока,
называются неоднородными.
• Закон Ома в интегральной форме:
сила тока в однородном проводнике
пропорциональна напряжению на
U
концах этого проводника
I
R
27.
• Законы Ома, Джоуля-Ленцастали одними из важнейших
открытий в области
электричества.
• Открытый Г. Омом в 1826 г.
закон, согласно которого на
участке цепи I=U/R и для
замкнутой цепи I = ЭДС/(R + r), а
также закон Джоуля-Ленца Q =
I*U*t для количества тепла,
выделяющегося при
прохождении тока по
неподвижному проводнику за
время t, заметно расширили
понятия об электричестве и
магнетизме.
28. Сопротивление
• Величина сопротивления R зависит от формы иразмеров проводника, а также от свойств
материала, из которого он сделан. Для
цилиндрического проводника
l
R
S
• - удельное электрическое сопротивление,
определяется химической природой вещества и
условиями, в которых он находится, в частности,
температурой.
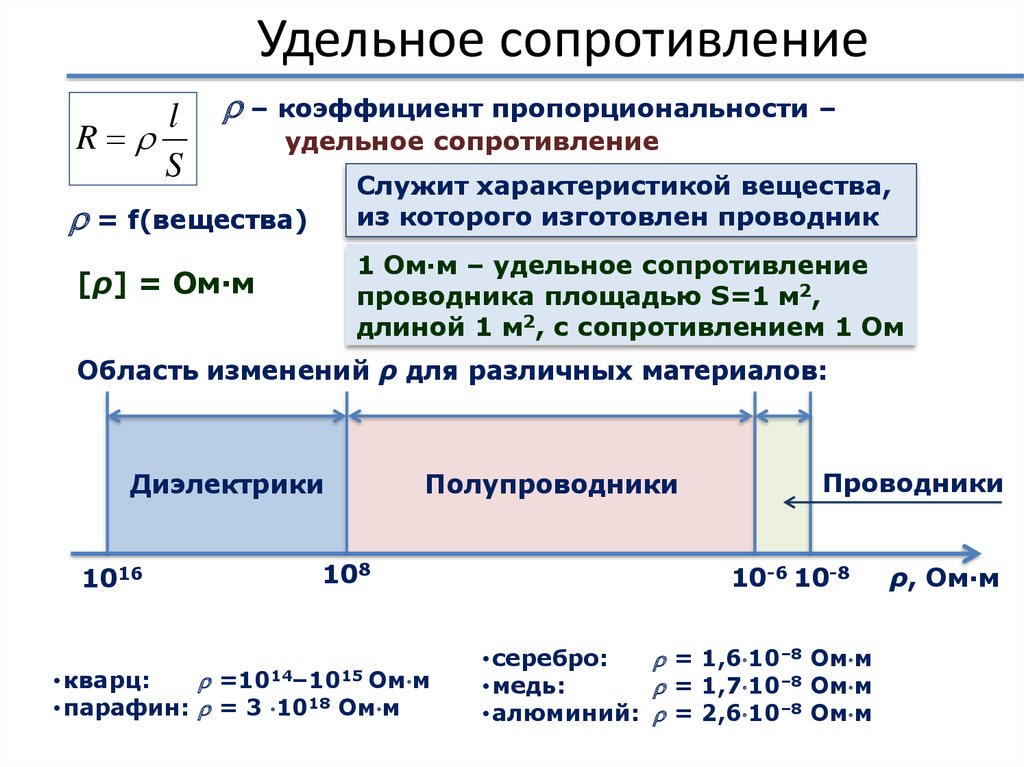
29. Удельное сопротивление
l – коэффициент пропорциональности –R
удельное сопротивление
S
Служит характеристикой вещества,
= f(вещества) из которого изготовлен проводник
1 Ом·м – удельное сопротивление
проводника площадью S=1 м2,
длиной 1 м2, с сопротивлением 1 Ом
[ρ] = Ом·м
Область изменений ρ для различных материалов:
Диэлектрики
1016
Полупроводники
108
•кварц:
=1014–1015 Ом м
•парафин: = 3 1018 Ом м
Проводники
10-6 10-8
•серебро:
= 1,6 10–8 Ом м
•медь:
= 1,7 10–8 Ом м
•алюминий: = 2,6 10–8 Ом м
ρ, Ом·м
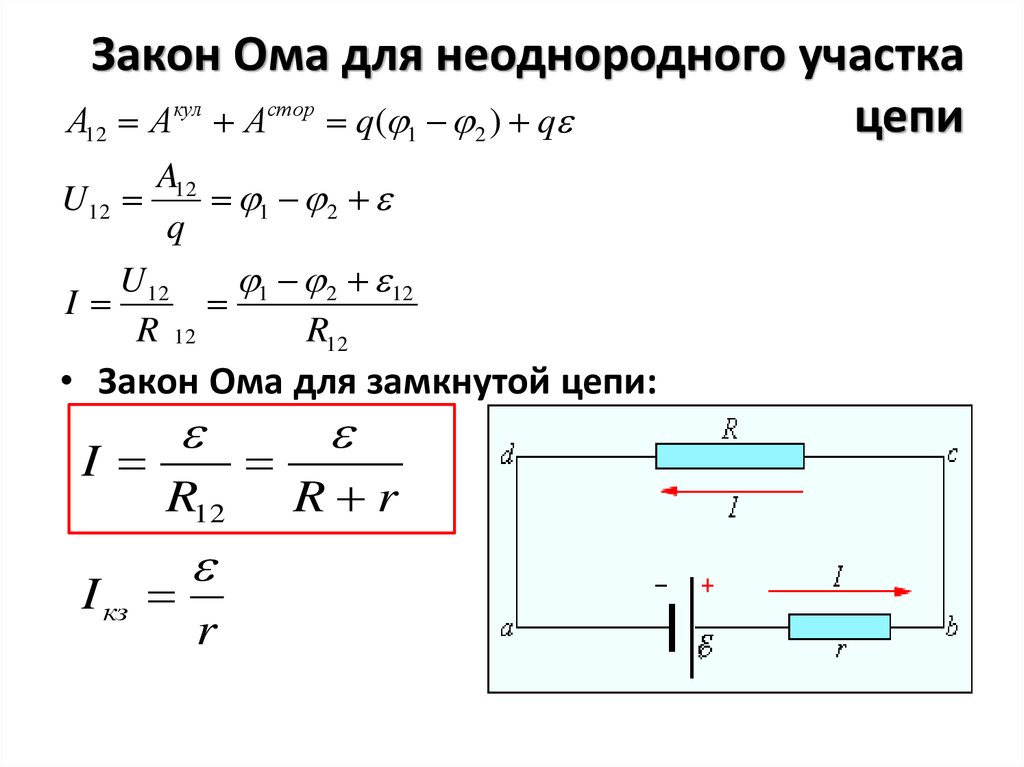
30. Закон Ома для неоднородного участка цепи
А12 Акул Астор q ( 1 2 ) qA12
U12
1 2
q
U12
1 2 12
I
R 12
R12
• Закон Ома для замкнутой цепи:
I
R12
I кз
r
R r
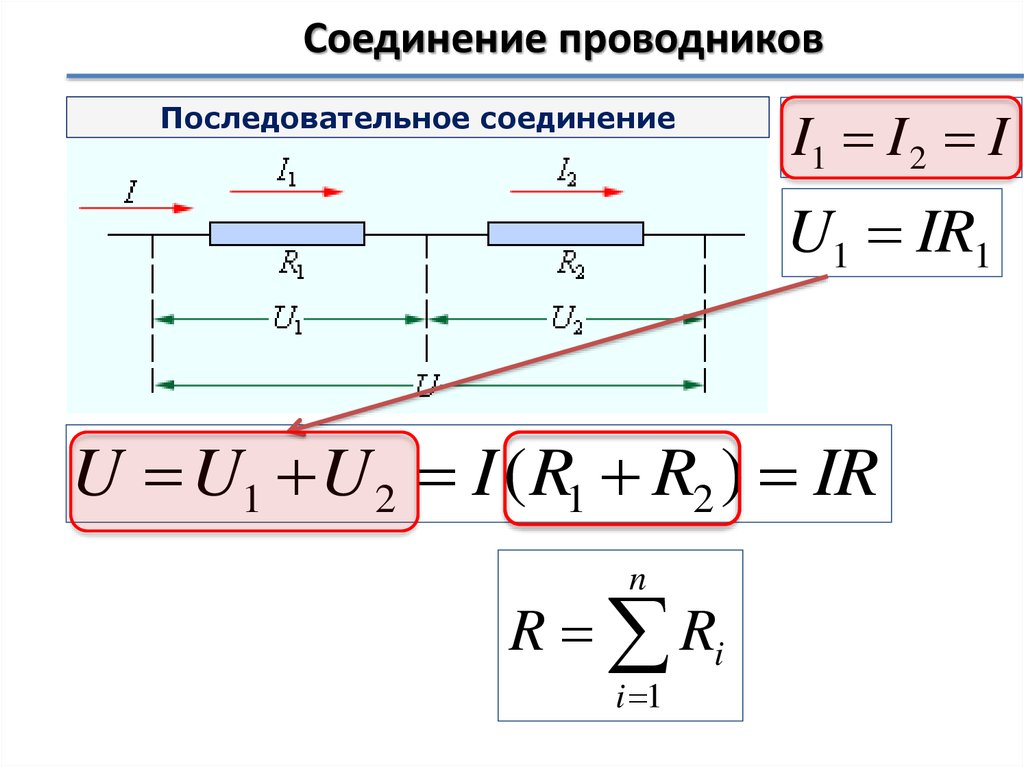
31. Соединение проводников
Последовательное соединениеI1 I 2 I
U1 IR1
U U1 U 2 I ( R1 R2 ) IR
n
R Ri
i 1
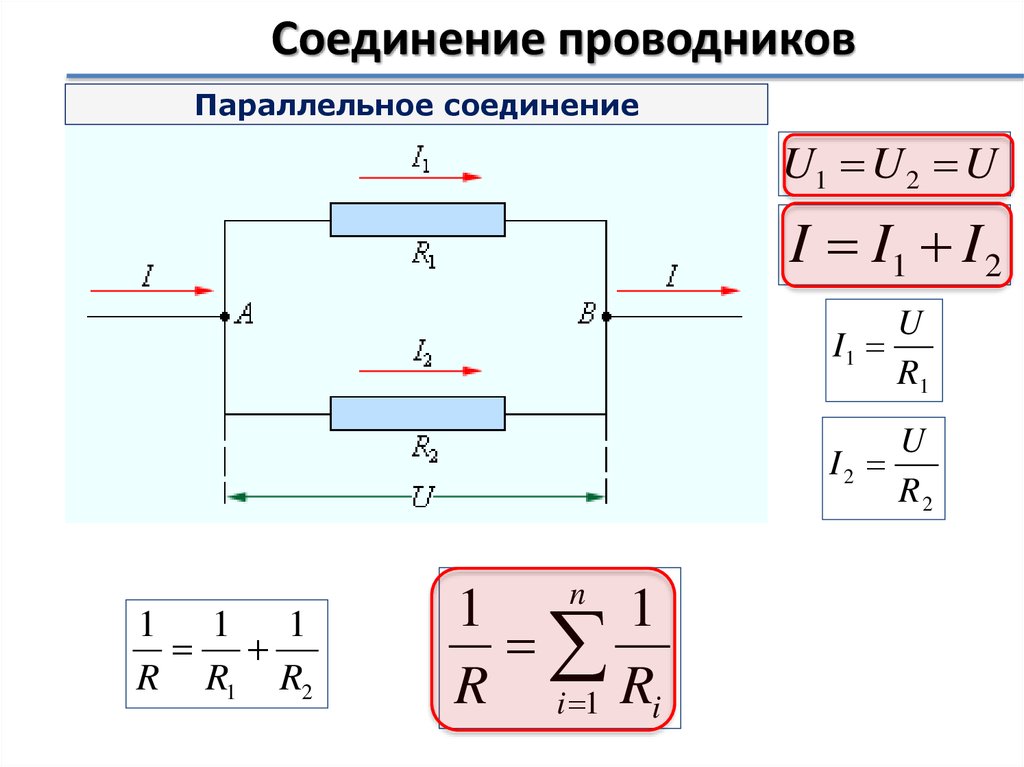
32. Соединение проводников
Параллельное соединениеU1 U 2 U
I I1 I 2
U
I1
R1
U
I2
R2
1 1
1
R R1 R2
n
1
1
R i 1 Ri
33. Закон Ома в дифференциальной форме
dSj
dl
j E,
1
удельная проводимость
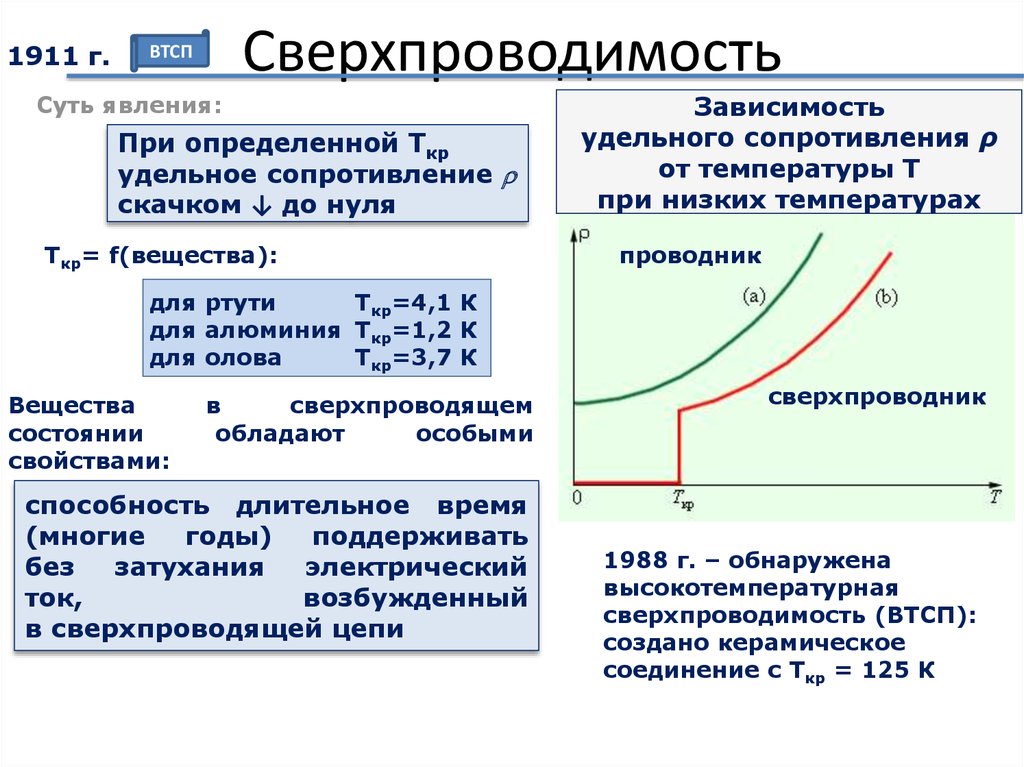
34. Сверхпроводимость
1911 г.Сверхпроводимость
ВТСП
Суть явления:
При определенной Tкр
удельное сопротивление
скачком ↓ до нуля
Tкр= f(вещества):
Зависимость
удельного сопротивления ρ
от температуры T
при низких температурах
проводник
для ртути
Tкр=4,1 К
для алюминия Tкр=1,2 К
для олова
Tкр=3,7 К
Вещества
состоянии
свойствами:
в
сверхпроводящем
обладают
особыми
способность длительное время
(многие
годы)
поддерживать
без
затухания
электрический
ток,
возбужденный
в сверхпроводящей цепи
сверхпроводник
1988 г. – обнаружена
высокотемпературная
сверхпроводимость (ВТСП):
создано керамическое
соединение с Ткр = 125 К
35. Закон Джоуля-Ленца
1840 г.Закон Джоуля-Ленца
Установили экспериментально
независимо друг от друга
Если ток проходит по неподвижному
металлическому проводнику, то вся
работа тока идет на его нагревание
Закон сохранения энергии
для однородного участка цепи
2
U
dQ
dt
R
dQ IUdt
dQ RI dt
2
dQ dA
Q – количество теплоты,
выделяемое
в цепи при прохождении тока





















 physics
physics








