Решение уравнений. Формулы сокращённого умножения. Теорема Виета

1.

х 50 х 49 0
4
2
х1 49
Нет
х2 1
решений
х1 7
х1 7, х 2 1
х2 1
х3 1, х4 7
Не верно!
Подумай!
Подумай!
Молодец!

2.

х 5 х 36 0
4
2
х1 3
Нет
х2 3
решений
Молодец!
Подумай!
х1 4
х1 3, х2 2
х2 9
х3 2, х4 3
Подумай!
Не верно!

3.

4 х 21х 5 0
4
2
х1 5, х2 5
Нет
х3 0,5, х4 0,5
решений
х1 0,25
х1 5
Молодец!
Не верно!
х2 5
Подумай!
Подумай!
х2 0,5

4.

3х 8 х 3 0
4
1
х1 Не верно!
3; х2
3
2
Нет
Подумай!
решений
1
1
1
х1 Молодец!
; х2
х1 Подумай
3; х2 !
3
3
3

5.

х 82 х 81 0
4
2
х1 1
Нет
х2 9
решений
Не верно!
х1 9; х2 9
Молодец!
х3 1; х4 1
Подумай!
х1 81
Подумай!
х2 1

6.

Решите
уравнение
№2(а)
х 8х
20
х 10
х 10
Нет
х1 10
Не верно!
Подумай!
решений
х2 2
2
х1 10
Подумай!
х2 2
х 10
Молодец!
х 1

7.

Решите
уравнение
№2(б)
х 8х
20
х 10
х 10
Нет
х 2
Не верно!
Подумай!
х1 0,5; х2 2 решений
2
х 2; х 2 х 2
Молодец!
Подумай!
х 0,5
х1 2; х2 0,5

8.

Решите
уравнение
№2(в)
5 х 3 3х 1
х 5
х 2
х 5; х 2 Нет
Не верно!
Подумай!
х1 1; х2 2
решений
х1 1
х 5, х 2
х2 1,5
х1 0,5, х2 1
Подумай!
Молодец!

9.

Решите
уравнение
№2(г)
1
3
72
2
3
х 6 х 6 х х 36 х
х 6; х 6
Нет
Молодец!
Подумай!
х 0; х 9
решений
х1 6
Не верно!
х2 9
х1 9
Подумай!
х2 6

10.

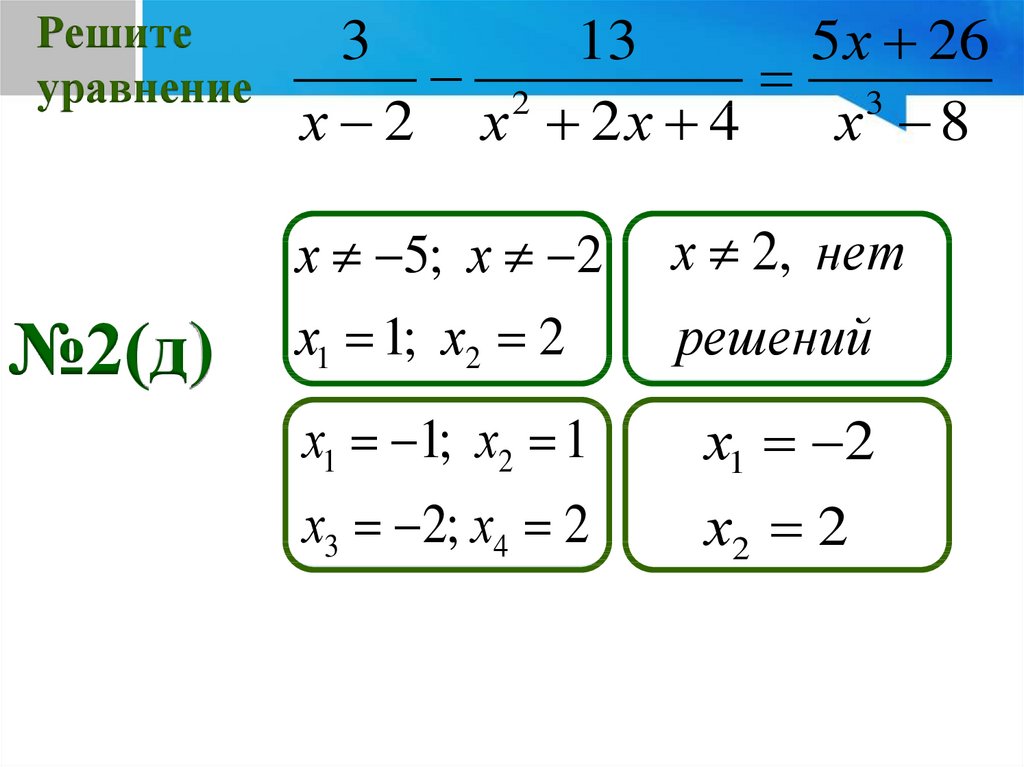
Решите
уравнение
№2(д)
3
13
5 х 26
2
3
х 2 х 2х 4
х 8
х 5; х 2
х 2, нет
х1 1; х2 2
решений
х1 1; х2 1
х1 2
Не верно!
Подумай!
х3 2; х4 2
Молодец!
Подумай!
х2 2

11.

Решите уравнение методом замены
переменной
х
2
2
9 4 х 9 3 0
2
№3(а)
х1 10
Нет
х2 12
решений
х1, 2 2 3
х1 10
Не верно!
Молодец!
х3, 4 10
Подумай!
Подумай!
х2 2 3

12.

Решите уравнение методом замены
переменной
х 5
4
10 х 5 9 0
2
№3(б)
х1 2; х2 4
Нет
х3 6; х4 8
решений
Не верно!
х1 1
Подумай!
х2 9
Подумай!
х1 8; х2 6
Молодец!
х3 4; х4 2

13.

Решите уравнение методом замены
переменной
х
2
2
3х 2 х 3х 8 0
2
№3(в)
х1 1; х2 1
Нет
х3 2; х4 4
решений
Не верно!
Подумай!
х1 2; х2 1 х1 4; х2 2
Подумай!
Молодец!
х3 1; х4 1
х3 1; х4 4

14.

Решите уравнение методом замены
2
2
переменной
х х 1 х х 2
№3(г)
х1 2
Нет
х2 1
решений
Молодец!
х1 1
Не верно!
х2 2
12
Подумай!
х1 1
Подумай!
х2 2

15.

Решите уравнение методом замены
переменной
х
4
2х
14 х
2 2
4
2 х 15
2
№3(д)
х1 3; х2 1
Нет
х3 1; х4 5
решений
х1 5 ; х2 1
х1 1
Не верно!
Молодец!
х3 1; х4 5
Подумай!
Подумай!
х2 5

16.

Решите
уравнение
х
3х
2 0
2
2 х 3 2 х 3
2
№4(а)
х1 3
Нет
х2 2
решений
х1 1,5
х1 3
Молодец!
Подумай!
х2 2
Подумай!
Не верно!
х2 2

17.

Решите
уравнение
№4(б)
х 1
3х
5
х
2 х 1
2
1
х1 Подумай
2; х2 !
4
1
х1Молодец!
2; х2
4
Нет
Подумай!
решений
1
х1 Не2;верно!
х2
4

18.

Решите
уравнение
№4(в)
х 3 х 2
1
4
х 2 х 3
4
3
285
х1, 2Не
верно!
6
х1 0,5
Подумай!
х2 0,5
Нет
Подумай!
решений
3
285
х1, 2Молодец!
6

19.

Решите
уравнение
1
2
6
2
2
2
х 3х 3 х 3х 4 х 3х 5
№4(г)
х1 2
Нет
х2 1
решений
х1 1
2
х1 Не
1;верно!
x2
3
Молодец!
Подумай!
х2 2
Подумай!

20.

Решите
уравнение
№4(д)
8
2
х 6 х 10
2
х 6 х 12
х1 4
Нет
х2 2
решений
х1 4
х1 4
Молодец!
Подумай!
х2 2
Подумай!
Не верно!
x2 2

21.

Скорость первого велосипедиста на 3 км/ч больше
скорости второго, поэтому 60 км он проезжает на 1 ч
быстрее второго. Найдите скорость каждого
велосипедиста.
№5(а)
60 км / ч
60 км / ч
70 км / ч
70 км / ч
60 км / ч
60 км / ч
Не верно!
Подумай!
70 км / ч
Подумай!
Молодец!
70 км / ч

22.

Поезд должен был проехать 360 км. Проехав 7 этого
12
расстояния, поезд увеличил скорость на
5 км/ч. Найдите скорость поезда на каждом участке
Движения, если на весь путь было затрачено 5ч.
№5(б)
70 км / ч
70 км / ч
Не верно!
Молодец!
3 км / ч
60 км / ч
65 км / ч
Подумай!
70 км / ч
75 км / ч
Подумай!
65 км / ч

23.

Моторная лодка прошла 35 км по озеру, а затем 34 км
по реке, впадающей в это озеро, за 2 ч. Найдите собственную скорость лодки, если скорость течения реки
составляет 1 км/ч.
№5(в)
Молодец!
35 км / ч
0,5 верно!
км / ч
Не
35
,5 км / !ч
Подумай
Подумай!
17
,5 км / ч

24.

Катер прошёл 20 км против течения реки и 16 км по
течению, затратив на путь против течения на 20 мин
больше, чем на путь по течению. Найдите собственную
скорость катера, если скорость течения реки 2 км/ч.
№5(г)
Подумай
12 км / ч!
Молодец!
22 км / ч
Не
верно!
10 км
/ч
22 км / ч или
Подумай!
10 км / ч

25.

Из пункта А в пункт В велосипедист ехал по дороге
длиной 10 км, а возвращался по дороге длиной в 12 км,
затратив на 5 мин меньше, чем на путь из пункта А в
пункт В. С какой скоростью ехал велосипедист из А в
В, если из В в А его скорость была на 4 км больше.
№5(д)
Подумай
28 км / ч!
Молодец!
12 км / ч
Не
верно!
40 км
/ч
12 км / ч или
Подумай!
40 км / ч

26.

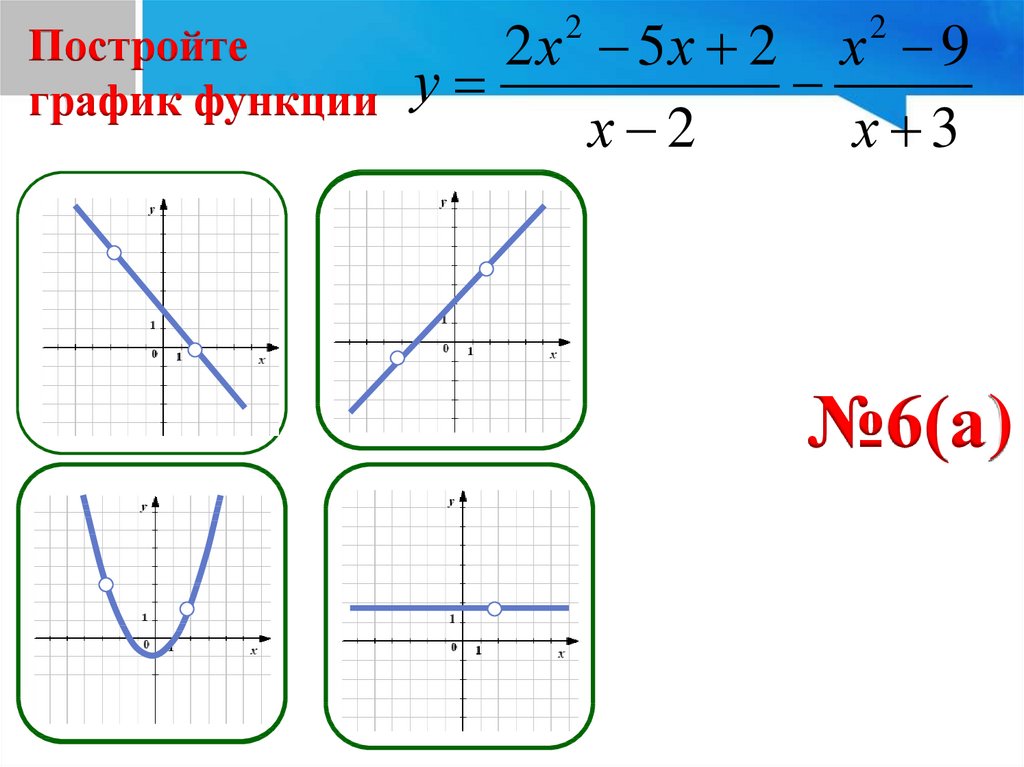
Постройте
график функции
Подумай
!
2 х 5х 2 х 9
у
х 2
х 3
2
2
Молодец!
№6(а)
Подумай
!
НЕ
верно!

27.

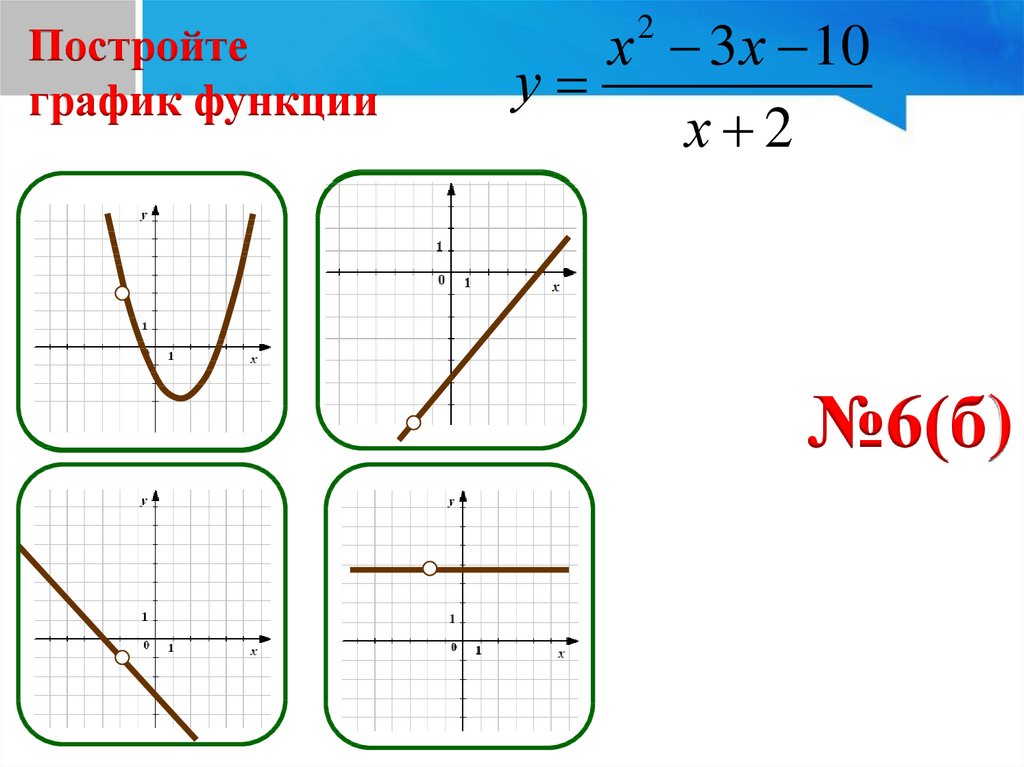
Постройте
график функции
Подумай
!
х 3 х 10
у
х 2
2
Молодец!
№6(б)
Подумай
!
НЕ
верно!

28.

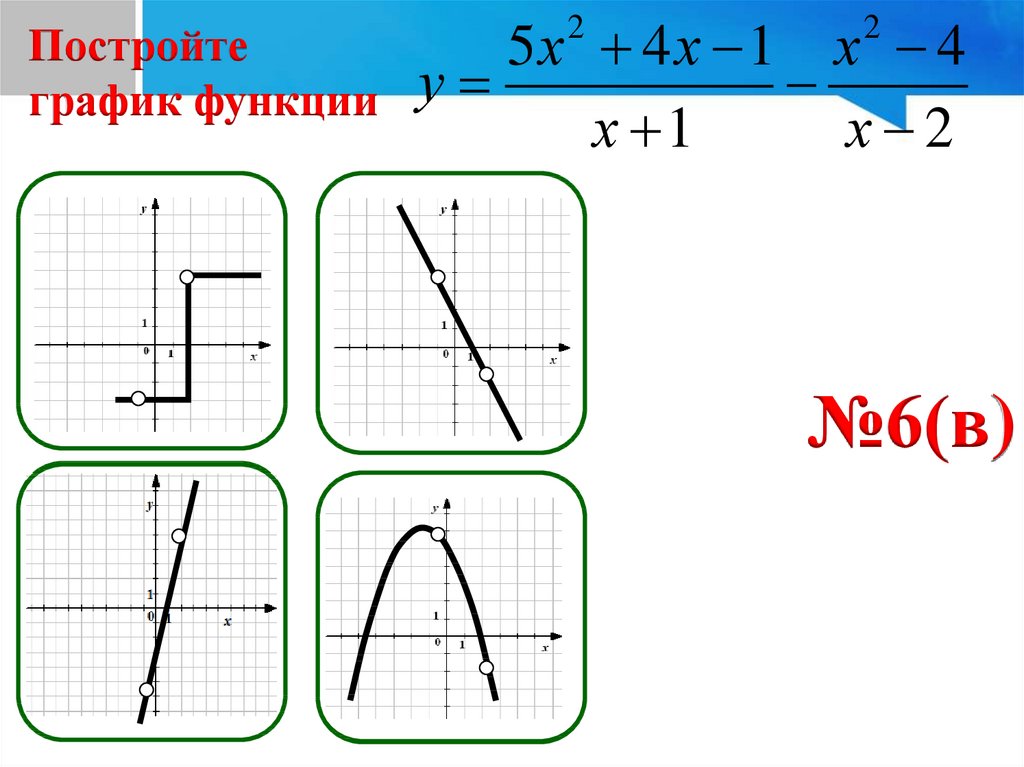
Постройте
график функции
НЕ
верно!
5х 4 х 1 х 4
у
х 1
х 2
2
2
Подумай
!
№6(в)
Молодец!
Подумай
!

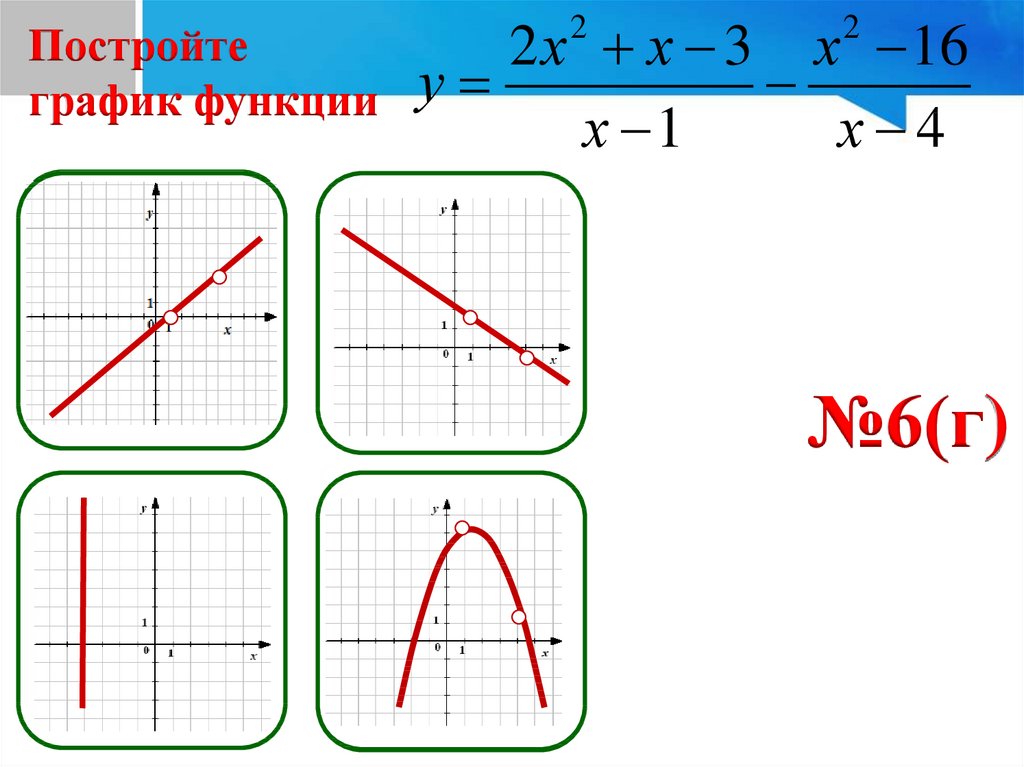
29.

Постройте
график функции
Молодец!
2 х х 3 х 16
у
х 1
х 4
2
2
Подумай
!
№6(г)
НЕ
верно!
Подумай
!

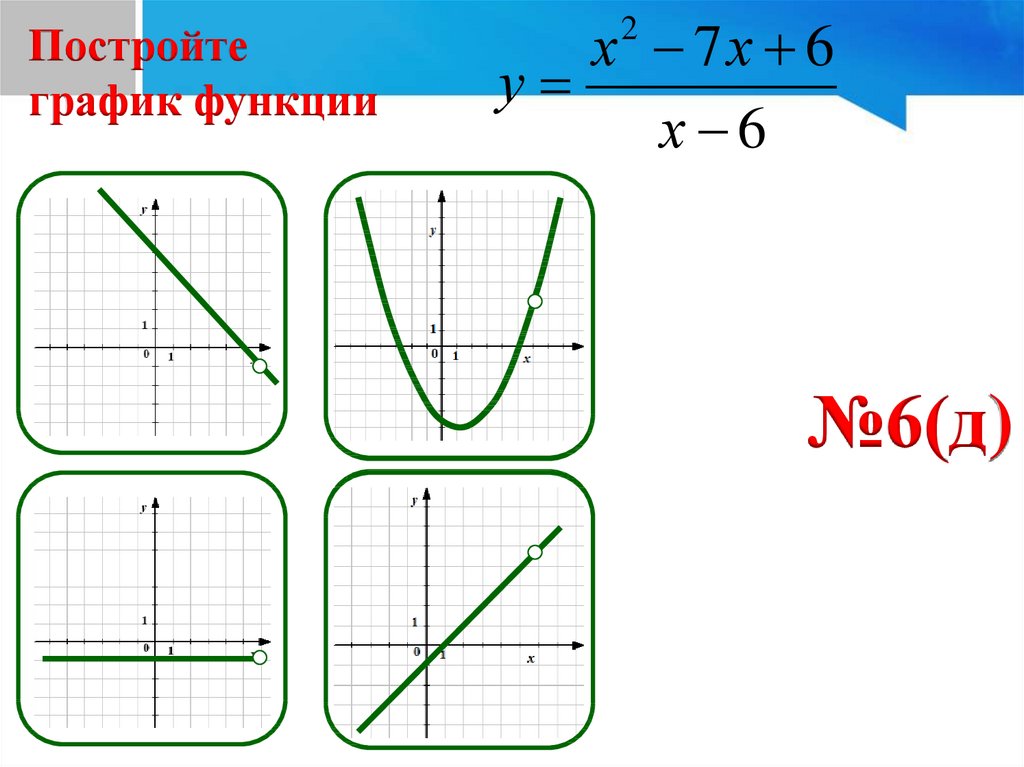
30.

Постройте
график функции
Подумай
!
х 7х 6
у
х 6
2
Подумай
!
№6(д)
НЕ
верно!
Молодец!

31.

Для перевозки 60 т груза заказали определённое количество автомобилей одинаковой грузоподъёмности. В
связи с поломкой двух автомобилей на каждый из
оставшихся погрузили на 1 т больше, чем планировалось. Сколько авто должно было работать на
перевозке груза?
№7(а)
Подумай
14 !
Не 10
верно!
Молодец!
12
Подумай!
12
или 10

32.

Двое рабочих, работая вместе, выполнили производственное
задание за 12 ч. За сколько часов может выполнить это
задание каждый рабочий самостоятельно, если один
из них может это сделать на 7 ч быстрее другого?
№7(б)
7чПодумай
. и 14! ч. 4Не
ч. иверно!
11ч.
ч. и 21ч.
21Подумай!
ч. и 28ч. 14Молодец!

33.

Слиток золота с серебром, содержащий 60 г золота,
сплавили с 60 г золота. Процентное содержание золота
в новом слитке на 15% больше, чем в исходном.
Сколько граммов серебра содержится в слитке?
№7(в)
Подумай
60г !
40 г
Молодец!
Не120
верно!
г
Подумай!
180 г

34.

В соляной раствор, содержащий 60 г воды, добавили
20 г воды, после чего концентрация соли уменьшилась
на 5%. Сколько граммов соли содержит раствор?
№7(г)
Подумай
260г !
Молодец!
20 г
Не 40
верно!
г
Подумай!
240 г

35.

Первая бригада на ремонте дороги работала 9ч, после чего
к ней присоединилась вторая бригада. Через 6 ч
совместной работы была отремонтирована половина
дороги. За сколько часов может отремонтировать
дорогу каждая бригада самостоятельно, если второй
бригаде для этого требуется на 9 ч меньше, чем первой
№7(д)
ч. и 45! ч.
45Молодец!
ч. и 36ч. 54Подумай
ч. и 54ч.
36Неч.верно!
и 27ч. 63Подумай!

36.

Теория
Неполные квадратные уравнения
ах 0
2
ах bx 0
2
ах c 0
2
ах c 0
2
х 0
b
х1 0, x2
a
с
с
х1 , х2
а
а
Корней нет

37.

Теория
Формула корней квадратного уравнения
ах bx с 0
2
D b 4ac
2
D 0
D 0
Нет корней
Один корень
D 0
Два корня
b D
х1
2a
b
х
2a
b D
х2
2a

38.

Теория
Теорема Виета
х2 - корни квадратного уравнения ах 2 bx с 0 ,
b
c
х1 х2
х1 х2
a
a
Если х1 и х2 - корни приведённого квадратного уравнения
2
х bx с 0 , то
х1 х2 b
х1 х2 c
Если х1 и
то
Теорема обратная теореме Виета
Если и таковы , что b и с
а
то эти числа - корни квадратного уравнения ах bx с 0 ,
a
2

39.

Теория
Квадратный трёхчлен
Квадратным трёхчленом называют многочлен вида
2
ах bx с , где х – переменная, a, b, c – некоторые числа
Корнем квадратного трёхчлена называют значение
переменной, при котором значение
квадратного трёхчлена равно НУЛЮ.
Если дискриминант квадратного трёхчлена ах 2 bx с
положительный, то данный трёхчлен можно разложить
на линейные множители:
ах bx с а х х1 х х2
2
где х1 и х2 - корни квадратного трёхчлена

40.

Теория
Формулы сокращённого умножения
a b a b a b
2
2
a b a 2ab b
2
2
2
a b a 2ab b
3
3
2
2
a b a b a ab b
2
2
2