Решение уравнений sinx=a. Понятие арксинуса числа

1. Решение уравнений sinx=a. Понятие арксинуса числа.

2.

Понятие арксинуса числа а
Число называют арксинусом
6
1
2
и записывают
1
arcsin
6
2
1
arcsin
6
2
Арксинусом числа a 1;1 называется такое число
; , синус которого равен а
2 2
arcsin a = α, если sinα = a и
2
2

3.

arcsin a = α, если sinα = a и
2
2
например
2
arcsin
2
4
и
2
так как sin
4
2
2
4
2
arcsin(-a)=-arcsina

4. АРКСИНУС ЧИСЛА

• Например
2
arcsin
;
2
4
arcsin 0 0;
3
arcsin
;
3
2
т.к.
т.к.
т.к.
2
; sin
.
2 4 2
4
2
2
0
2
; sin 0 0.
3
; sin
.
2 3 2
3 2

5. АРКСИНУС ЧИСЛА ОСНОВНЫЕ ФОРМУЛЫ

• Например
2
2
1
1
2 arcsin 3 arcsin
2 arcsin
2
2
2
2
3
13
3 2
4
6
4
3
12
1
3
2.
2 arcsin 1 5 arcsin 0
arcsin
2
2
1. 3 arcsin
1
3
arcsin
2 5 0
2
2
2
1
7
2 3
6
6

6.

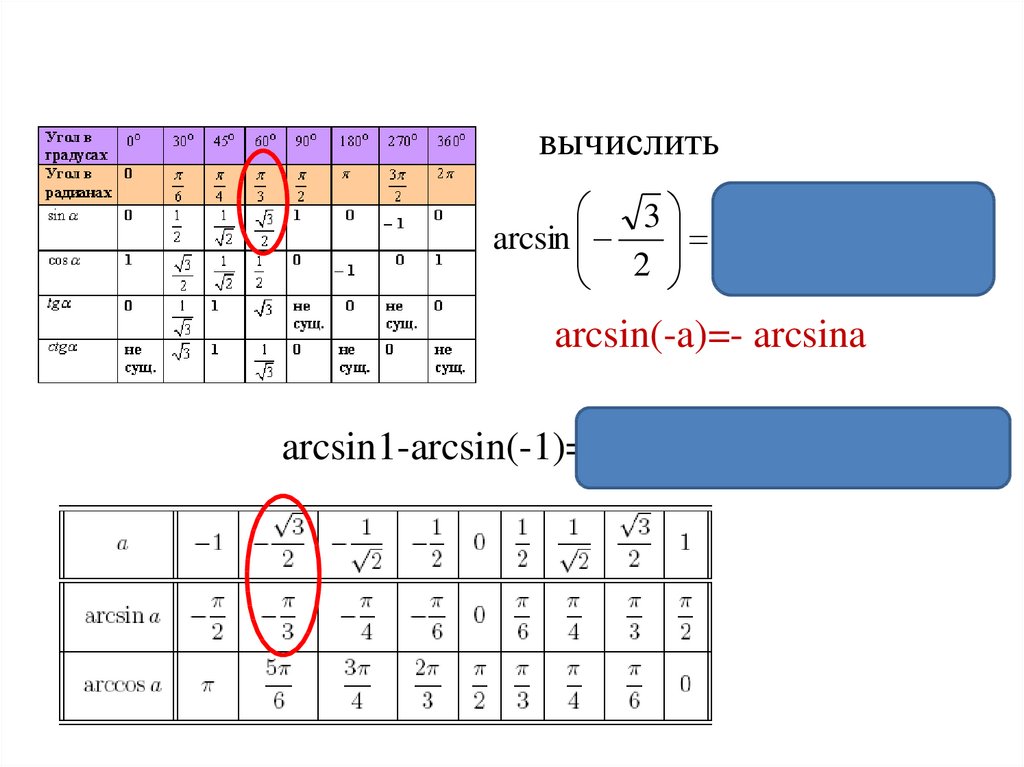
вычислить
3
3
arcsin
arcsin
2
2
3
arcsin(-a)=- arcsina
arcsin1-arcsin(-1)=arcsin1+arcsin(1)= 2 2

7.

Определим, имеют ли смысл выражения:
Выражение имеет смысл, если удовлетворяет условию
1 sin x 1
1) arcsin (√5) - выражение не имеет смысла, так как √5 > 1;
2) arcsin (√2/3) - выражение имеет смысл, так как – 1
√2/3
1;
3) arcsin (-π/5) - выражение имеет смысл, так как – 1
- π /5
1;
4) arcsin (-√3) - выражение не имеет смысла, так как -√3 < -1.

8. При каких значениях х имеет смысл выражение:

1. arcsin(x²-1)
-1≤ х²-1 ≤ 1
0 ≤ х² ≤2
Ответ:
2.arcsin(5-2x)
-
1≤ 5-2х ≤1
-6≤ -2х ≤ -4
2≤ х ≤3
Ответ: [2;3]

9.

Решить уравнение sin x=a
По определению:
синусом углаα называется ордината точки
-1
0
1
И значит определения синуса
следует, что 1 sin x 1
Поэтому, если sinx = 2,5, то уравнение
не имеет корней т.к 2,5>1
уравнение sinx= -1,5 тоже не имеет корней
т.к -1,5<-1

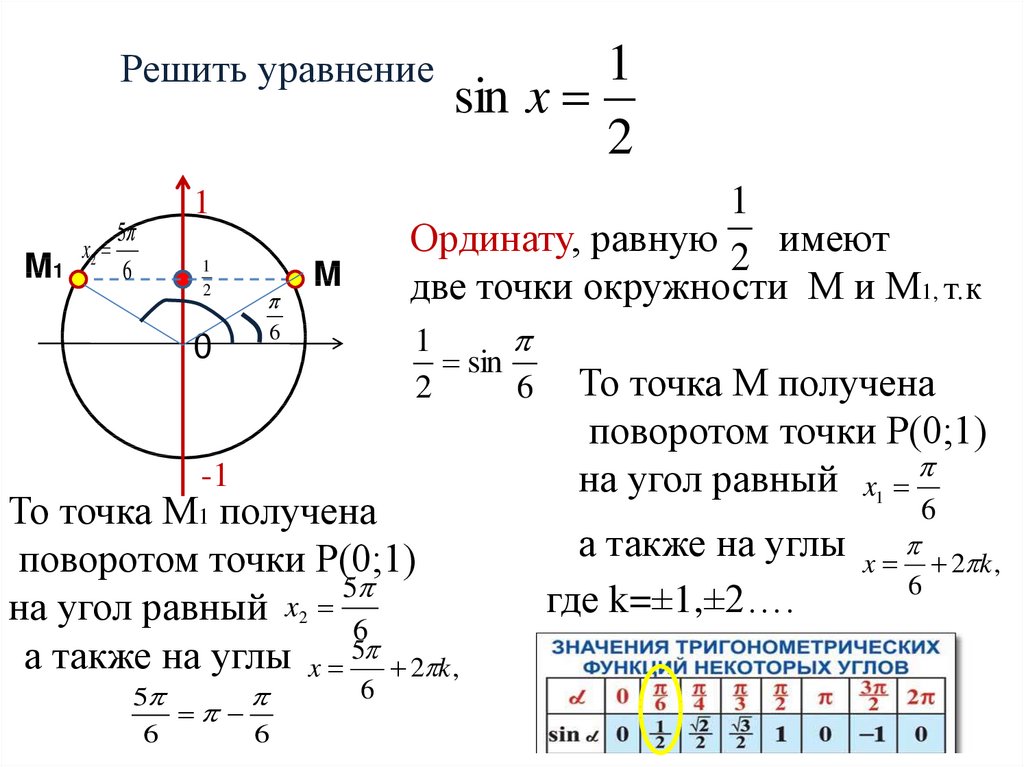
10.

Решить уравнение
M1
x2
5
6
1
Ординату, равную 2 имеют
две точки окружности М и М1, т.к
1
1
2
0
1
sin x
2
M
1
sin
2
6
6
-1
То точка М1 получена
поворотом точки Р(0;1)
5
на угол равный x2 6
а также на углы x 5 2 k ,
5
6
6
6
То точка М получена
поворотом точки Р(0;1)
на угол равный x1
а также на углы
где k=±1,±2….
x
6
6
2 k ,

11.

Получили , что решением уравнения являются
х1
6
2 k
x2
6
где k=±1,±2….
2 k
Эти 2 корня можно объединить в одну формулу
x ( 1)
n
6
n, n Z

12.

1
sin x
2
значит x1 6 2 k
5
6
1
2
6
5
x2
2 k
6
k Z
Объединим в одну формулу
x ( 1) n n,
6
n Z
n 1
x
(
1
)
n,
Преобразуем ее по свойствам
6
степени в вид
n Z

13. Уравнение sinx=a

1
sin 2 x
2
1
2 x 1 arcsin n
2
n
2 x 1
n
x 1
n
Ответ:
1 n
12
n
2
12
6
, n Z.
n
n
2
, n Z.

14.

вывод
Корни уравнения sin x=a
Выражаются общей формулой
Если а > 0, то
x ( 1) n n,
6
n Z
Если а< 0,то
x ( 1) n n,
6
n Z

15. Солнышко, запомни

sin x 5
3
sin x
2
2
sin x
2
Корней нет
x 1 k , k Z
6
k
x 1
k 1
4
k , k Z

16.

Решить уравнение
2
sin x
3
2
x ( 1) arcsin
n,
3
n Z
n

17.

Решить уравнение
x
2 sin 1
3
x
1
sin
3
2
х
1
n
( 1) arcsin
n, n Z
3
2
arcsin( a) arcsin a
х
1
( 1) n arcsin
n, n Z
3
2
х
1
n 1
( 1)
arcsin
n, n Z
3
2

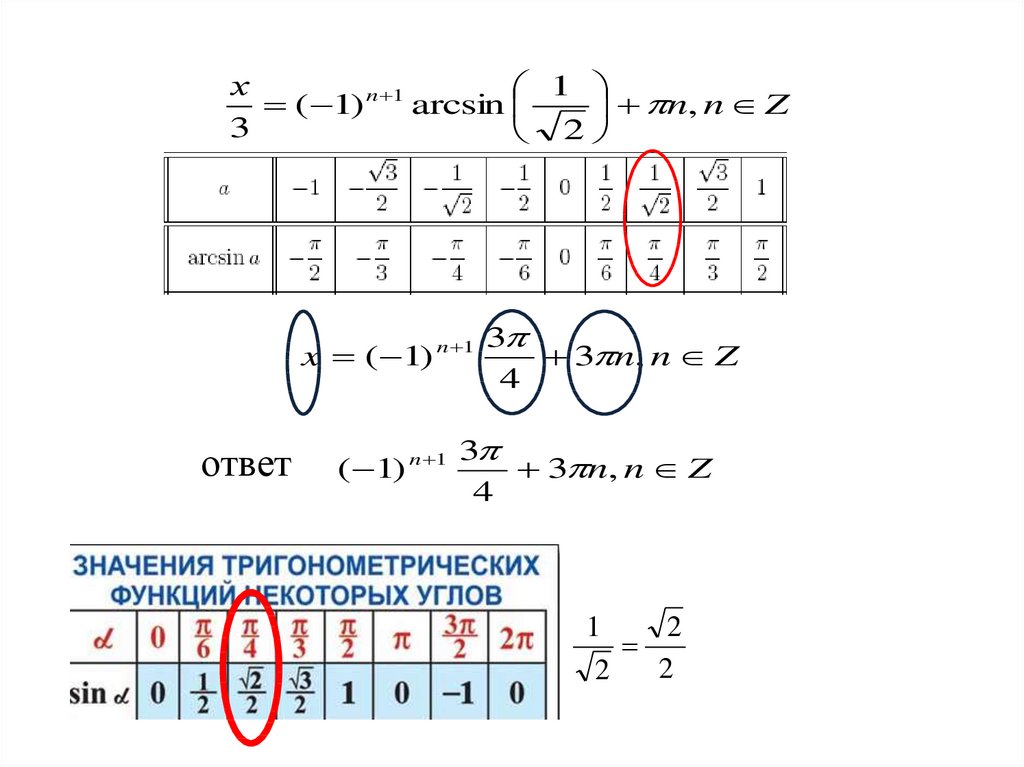
18.

х
1
( 1) n 1 arcsin
n, n Z
3
2
x ( 1) n 1
ответ
( 1)
n 1
3
3 n, n Z
4
3
3 n, n Z
4
1
2
2
2

19. Уравнение sinx=a

3sin x 1 2 sin x 1 0
3sin x 1 0;
2sin x 1 0;
1
sin x ;
3
1
sin x ;
2
1
x 1 arcsin n, n Z .
3
n
x ( 1)
n 1
n,
6
n Z
1
Ответ: 1 arcsin 3 n, n Z .
n
( 1)
n 1
n, n Z
6

20. Обратите внимание, никаких х в ответе нет, тем более с индексами

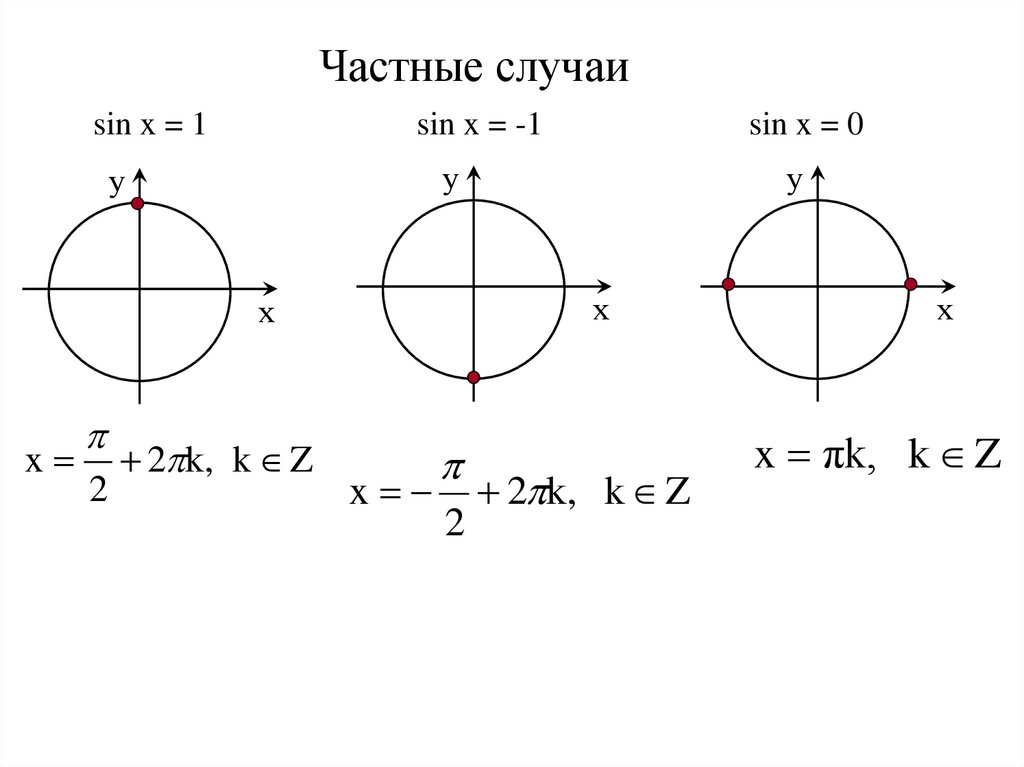
21.

Частные случаи
sin x = 1
sin x = -1
у
у
x
2
2 k, k Z
у
х
х
sin x = 0
x
2
2 k, k Z
х
x πk, k Z

22. Тренируемся решать:

1. Sin 5x = 1
5x
2
2 k, k Z
2
k, k Z
x
10 5
2
k, k Z
Ответ :
10 5

23. Тренируемся решать:

sin x
0
4
x
4
x
4
n, n
n, n
Ответ :
4
n, n