Similar presentations:
Mathematics for Computing. Lecture 2: Logarithms and indices
1. Mathematics for Computing
Lecture 2:Logarithms and indices
Dr Andrew Purkiss
The Francis Crick Institute
or
Dr Oded Lachish, Birkbeck College
E-mail: mfc@dcs.bbk.ac.uk
2. Material
What are Logarithms?Laws of indices
Logarithmic identities
3. Exponents
02 =1
1
2 = 2
2
2 = 2 x 2 = 4
23 = 2 x 2 x 2 = 8,
…
n
2 = 2 x 2 x … with n 2s
-1
2 ==
-2
2 = =
2-3 = =
…
2-n = =
4. Problem
We want to know how many bits thenumber 456 will require when stored in
(non signed) binary format.
Solution based on what we learned last
week: Convert the number to Binary and
count the number of bits
After counting we get 9 (check it out)
There is a simpler way
Digit
numb
er
Numb
er
Remainder
when
dividing by 2
1
2
3
4
5
6
7
8
9
456
228
114
57
28
14
7
3
1
0
0
0
1
0
1
1
1
1
5. A simpler way
Round 456 up to the smallest power of 2 that is greater than 456.Specifically, 512.
The answer!
9
Notice that 512 = 2 .
Why did we round up?
index
9
8
7
6
5
4
3
2
1
0
1
1
0
1
0
1
0
1
0
0
0
1
0
0
0
0
0
0
0
456
512
29
This gives us 2 to the power of the 1 + the index of the MSB of our number,
which is 1 less than its number of bits because the indices start from 0!
6. A simpler way
Much better, but we really don’t like the rounding up to thesmallest …
Don’t worry we just did this specific rounding up so that the
answer comes out nicely.
We will show a simpler way to do this (although we will start with
512 since it is nicer)
7. Logarithms
If we already knew the 512, then we would wonder which number is suchthat
2x = 512
In words, how many times do we need to multiply 2 by itself to get 512?
The formal way to write this is x = log2512 , which means how many times do
we need to multiply 2 by itself to get 512?
We already know the answer is 9.
This is interpreted as follows:
8. Logarithms
We only know 456, lets compute log base 2 of 456log2456 = 8.861…
Rounding this number up gives the answer we wanted, 9!
Why didn’t we get an integer? Because 456 is not a power of 2 so to get 456
we need to multiply 2 by itself 8.861 times, which can be done once we know
what this means.
So, how many bits do need in order to store the number 3452345 in binary
format?
9. Logarithms
If x = yzthen z = logy x
10. Logarithms and Exponents
If x = yzthen z = logy x
e.g. 1000 = 10 3,
then 3 = log10 (1000)
The base
11. Logarithms and Exponents: general form
From lecture 1) base index form:number = baseindex
then index = logbase (number)
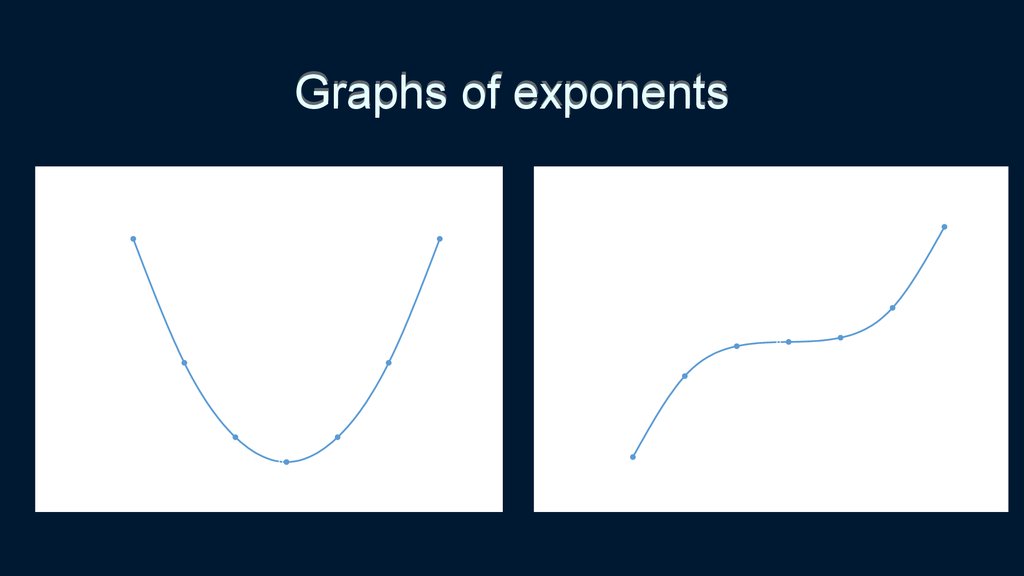
12. Graphs of exponents
x^2x^3
10
30
9
20
8
7
10
6
5
X^2
X^3
0
-4
4
-3
-2
-1
0
-10
3
2
-20
1
-4
-3
-2
-1
0
0
x
1
2
3
4
-30
x
1
2
3
4
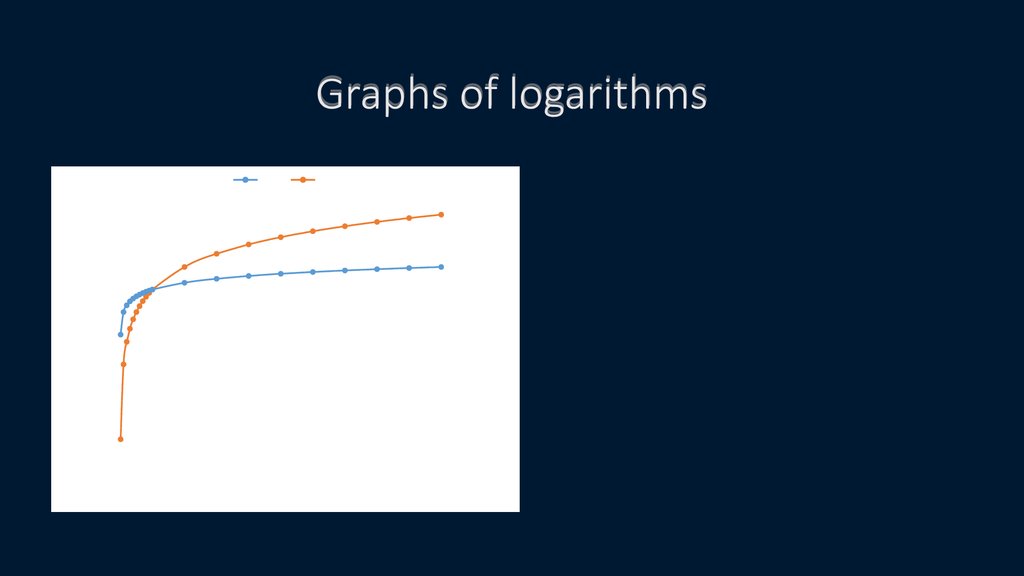
13. Graphs of logarithms
Log10Log2
4
2
0
Logn(x)
0
2
4
6
-2
-4
-6
-8
x
8
10
12
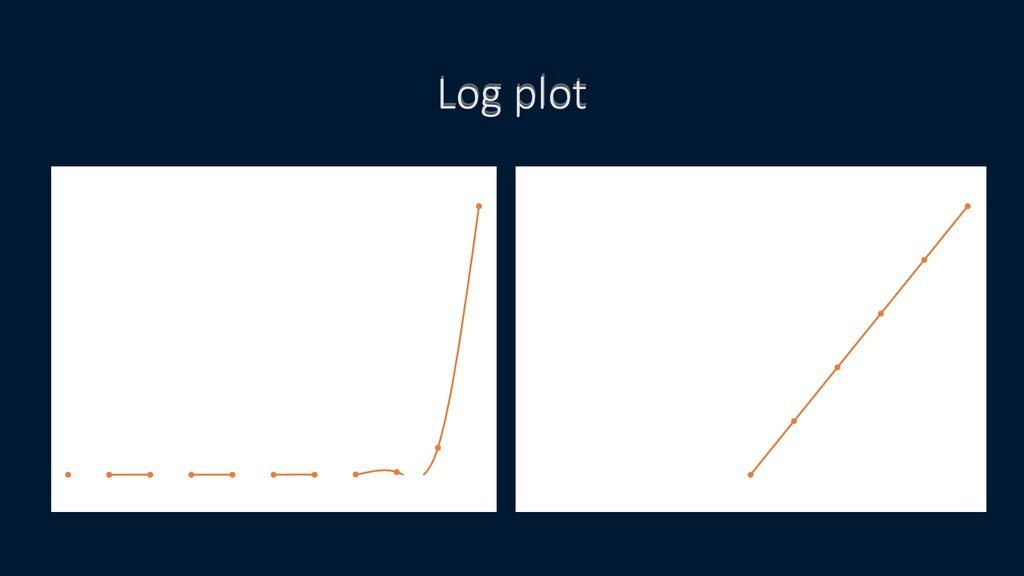
14. Log plot
10^x10^x
100000
100000
80000
10000
60000
1000
10^x
-5
10^x
-4
-3
-2
-1
40000
100
20000
10
0
0
x
1
2
3
4
5
-5
-4
-3
-2
-1
1
0
x
1
2
3
4
5
15. Three ‘special’ types of logarithms
Common Logarithm: base 10Common in science and engineering
Natural Logarithm: base e (≈2.718).
Common in mathematics and physics
Binary Logarithm: base 2
Common in computer science
16. Laws of indices
1) a0 = 12) a1 = a
17. Laws of indices
1) a0 = 12) a1 = a
Examples:
20 = 1
100 = 1
18. Laws of indices
1) a0 = 12) a1 = a
Examples:
21 = 2
101 = 10
19. Laws of indices
3) a-x = 1/ax20. Laws of indices
3) a-x = 1/axExample:
3-2 = 1/32 = 1/27
21. Laws of indices
4) ax · ay = a(x + y)(a multiplied by itself x times) · (a multiplied by itself y times) = a multiplied by itself x+y times
5) ax / ay = a(x - y)
(a multiplied by itself x times) divided by (a multiplied by itself y times) = a multiplied by itself x-y times
22. Laws of indices
4) ax · ay = a(x + y)42 · 43 = 4(2+3) = 45
16x64 = 1024
9 · 27 = 32 · 33 = 3(3 + 2) = 35= 243
25 · (1/5) = 52 · 5-1 = 5(2-1) = 51= 5
23. Laws of indices
5) ax / ay = a(x - y)105 / 103 = 10(5-3) = 102
100,000 / 1,000 = 100
23 / 27 = 2(3-7) = 2-4
8 / 128 = 1/16, [24 = 16, 2-4 = 1/16, see law 3)]
64 / 4 = 26 / 22 = 2(6- 2) = 24 = 16
27 / 243 = 33 / 35 = 3(3 - 5) = 3-2= 1/9
25 / (1/5) = 52 / 5-1 = 5(2+1) = 53= 125
24. Laws of indices
6)(ax)y = axy
(a multiplied by itself x times) multiplied by itself y times) = a multiplied by itself x ·y times
X times
X times
X times
(a ·a ·…) ·(a ·a ·…) ·…(a ·a ·…)
y times
7)
ax/y =
y
a1/y is the number you need to multiply by itself y times to get a. (a1/y)y = ay/y = a1 =a
1/2
1/3
So , 2 is square root of 2, which is, and 3 is square root of 3, which is,
25. Laws of indices
6) (ax)y = axy(103)2 = 10(3x2) = 106
1,0002 = 1,000,000
(24)2 = 2(2x4) = 28
162 = 28 = 256
81 = (9) 2 = (32)2 = 34 = 81
1/16 = (1/4) 2 = (2-2)2 = 2-4 = 1/16
26. Laws of indices
7) ax/y = y√ax10(4/2) = 2√104
102 = 2√10,000 = 100
2(9/3) = 3√29
23 = 3√512 = 8
8 = 23 = 26/2 = 2√64 = 8
1/7 = (7) -1 = (7) -2/2 = 2√(1/49) = 7
27. Logarithmic identities
‘Trivial’Log form
logb 1 = 0
logb b = 1
Index form
b0 = 1
b1 = b
28. Logarithmic identities 2
y · logb x = logb xyDefinition of log
(bx)y = bxy
Definition of log
29. Logarithmic identities 2 examples
y · logb x = logb xy(bx)y = bxy
Examples:
9 = 3 · log 8 = log 83 = log 512 = 9
2
2
2
512= (8)3 = (23)3 = 23·3= 29 = 512
30. Logarithmic identities 3
Negative Identity-log x = log (1/x)
b
b
b-x = 1/bx
Addition
log x + log y = log xy
b
b
b
bx · by = b(x + y)
Subtraction
log x - log y = log x/y
b
b
b
bx / by = b(x - y)
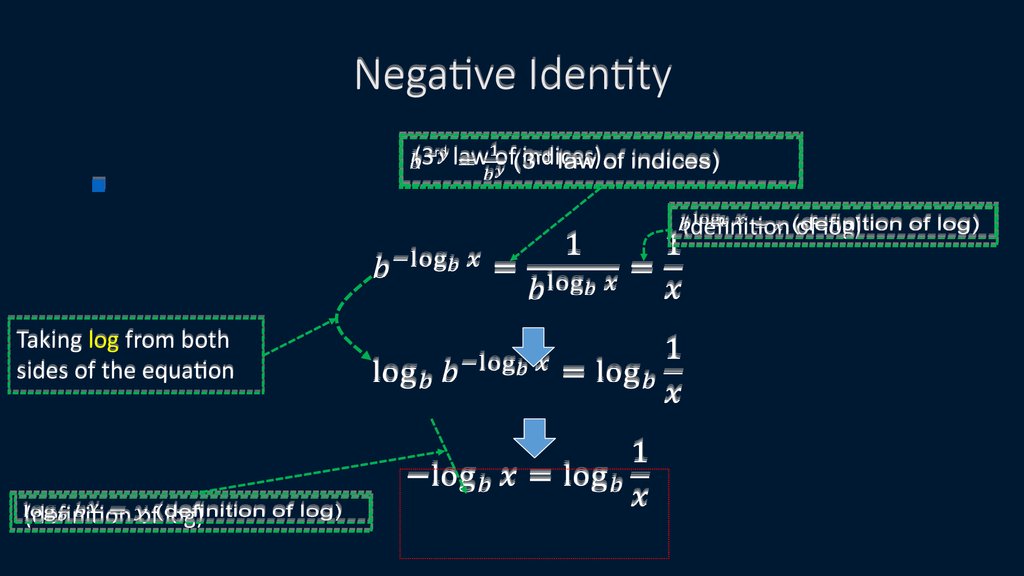
31. Negative Identity
(3rd law of indices)(definition of log)
Taking log from both
sides of the equation
(definition of log)
32. Negative identity
Negative Identity-log x = log (1/x)
b
b
b-x = 1/bx
Examples:
-3 = -log 8 = log (1/8) = -3
2
2
1/8 = 2-3 = 1/23 =1/8
33. Addition identity
bx · by = b(x + y) (4th law of indices)Taking log from
both sides of the
equation
Definition of log
(definition of log)
34. Addition identity examples
Additionlog x + log y = log xy
b
b
b
bx · by = b(x + y)
Examples:
5= 2+3 = log 4 + log 8 = log 4·8 = log 32 = 5
2
2
2
2
32= 4 · 8 = 22 · 23 = 2(2 + 3) = 25 = 32
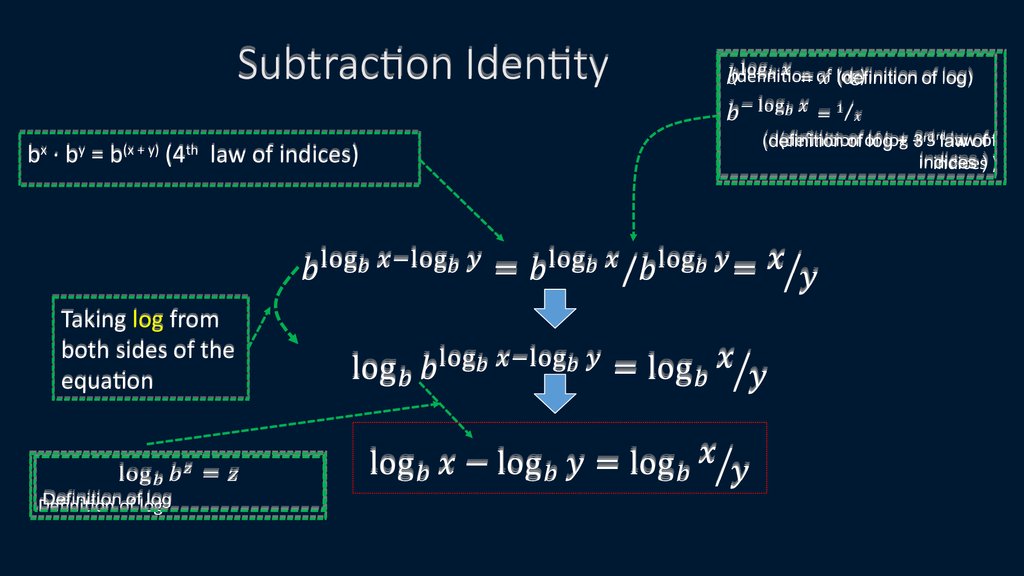
35. Subtraction Identity
b ·b =bx
y
(x + y)
(4 law of indices)
th
Taking log from
both sides of the
equation
Definition of log
(definition of log)
(definition of log + 3rd law of
indices )
36. Subtraction identity examples
Subtractionlog x - log y = log x/y
b
b
b
bx / by = b(x - y)
Examples:
-1 = 2-3 = log 4 - log 8 = log 4/8 = log 1/2 = -1
2
2
2
2
1/2= 4 / 8 = 22 / 23 = 2(2 - 3) = 2-1 = 1/2
3 = 5-2 = log2 32 - log2 4 = log2 32/4 = log2 8 = 3
8= 32 / 4 = 25 / 22 = 2(5 - 2) = 23 = 8
37. Changing the base
logb x = logy x / logy bleads to
logb x = 1/(logx b)
38. Changing the base, examples 1
logb x = logy x / logy bExamples:
2 = log4 16 = log2 16 / log2 4 = 4/2= 2
4 = log3 81 = log5 81 / log5 3
39. Changing the base, examples 2
logb x = 1/(logx b)Examples:
2 = log 16 = 1/log 4 = 1/(1/2)= 2
4
16
4 = log3 81 = 1/ log81 3
= 1/(1/4)= 4
















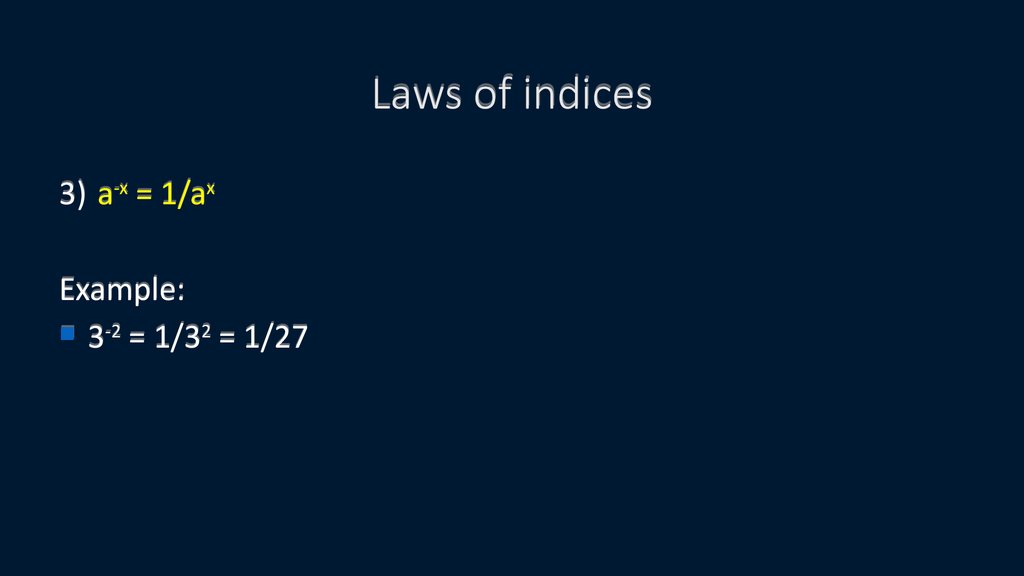

















 mathematics
mathematics








