Similar presentations:
Describe mathematical patterns in living organisms
1.
Mathematics is the language in which the book of nature is written .(G.Galileo)
2.
Describe mathematical patterns in living organismsAssessment criteria:
1. Explains mathematical laws in living organisms
2. Describes the relationship between nature and mathematics.
3.
OrganismsKey concept: Systems
Related concept: Form, Function
Global context: Identities and relationships
Statement of inquiry:
Human identity includes the impulse to help family members and also those we are not
closely related to.
4.
The first and very striking example is sunflowers . Their seeds are distributedin such a way that they maximize the use of the entire social area without losing a
single millimeter . And they are arranged in the form of two intersecting spirals from
right to left and vice versa .
5.
Something similar happens with pineapple cells , he has 8right - sided spirals , 3 left - sided , and 21 vertical
6.
In a pine cone , if you look closely , you can see 2 spirals , one twisted clockwiseand the other counterclockwise . The number of these spirals is 8 and 13 .
7.
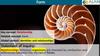
The shells of the mollusks are twisted in a spiral , and if you measureits curls , then their ratio is constant and equal to 1.618
8.
A hurricane or tornado is spiraling …9.
Or here , for example , the simplest waves also spiral10.
If you look at the flight of abird , from the front or from
behind in slow motion
In action , it can be seen that
the trajectory of the wings
during flight
Is a graph of the functions of
an algebraic equation
Namely , parabolas y=ax^2 +bx
+ c . Obviously , when flying
The wings rise up and down .
To depict this phenomenon,
It is possible to construct
parabolas defining the strokes .
When lowering the wings of
the bird, the outlines of
parabolas are also visible, but
with the branches pointing
down, T, e, the value of a is
less than 0 .
11.
At fixed points in time , if you look at fish from above or from below , you cancharacterize their shape in the form of both algebraic and trigonometric
functions . When swimming , the body of the fish takes the form of a curve that
resembles the graph of the function of a cubic parabola , namely
y=x^3
12.
Describe mathematical patterns in living organismsAssessment criteria:
1. Explains mathematical laws in living organisms
2. Describes the relationship between nature and mathematics.












 mathematics
mathematics biology
biology