Наибольшее и наименьшее значения функции

1.

2.

функция возрастает
Предположим, что функция f
не имеет на отрезке [а; b] критических
точек.
наибольшее
значение
наименьшее
значение
Тогда она возрастает (рис. 1) или
убывает (рис. 2) на этом отрезке.
a
b
функция убывает
наибольшее
значение
наименьшее
значение
a
b
Значит,
наибольшее и наименьшее значения
функции f на отрезке [а; b] — это
значения в концах а и b.

3.

Примеры
Пусть теперь функция f имеет на
отрезке [а; b] конечное число
критических точек.
наибольшее
значение
наименьшее
значение
a c
b
наибольшее
значение
наибольшее
значение
наименьшее
значение
наименьшее
значение
a c
n b
Наибольшее и наименьшее
значения функция f может
принимать в критических точках
функции или в точках а и b.
Чтобы найти наибольшее и
наименьшее значения функции,
имеющей на отрезке конечное
число критических точек, нужно
вычислить значения функции во
всех критических точках и на
концах отрезка, а затем из
полученных чисел выбрать
наибольшее и наименьшее.

4.

1.
Найдите наименьшее значение функции y = x3 – 27x на отрезке [0; 4]
Значения функции в
концах отрезка.
1) y(0) = 0
y(4) = 43– 27 4 = – 44
3
-3
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(3) = 33– 27 3 = –54
Выбрать наименьшее из
полученных значений.
x = 3 [0; 4]
x = –3 [0; 4]
Ответ
- 5 4
3
1 0 х
х

5.

Выполнение этапов решения можно изменить, как вам удобно.
Этапы
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее или
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
x = 3 [0; 4]
x = –3 [0; 4]
3) y(0) = 0
y(4) = 43– 27 4 = – 44
y(3) = 33– 27 3 = –54
Ответ
- 5 4
3
1 0 х
х

6.

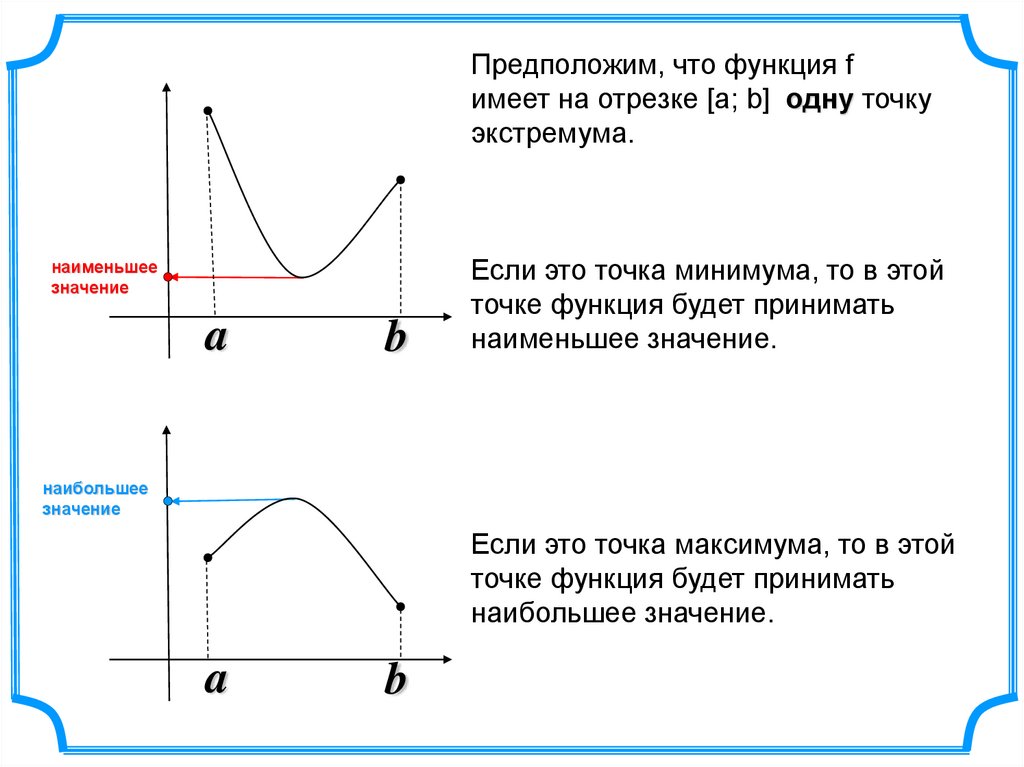
Предположим, что функция f
имеет на отрезке [а; b] одну точку
экстремума.
наименьшее
значение
a
b
Если это точка минимума, то в этой
точке функция будет принимать
наименьшее значение.
наибольшее
значение
Если это точка максимума, то в этой
точке функция будет принимать
наибольшее значение.
a
b

7.

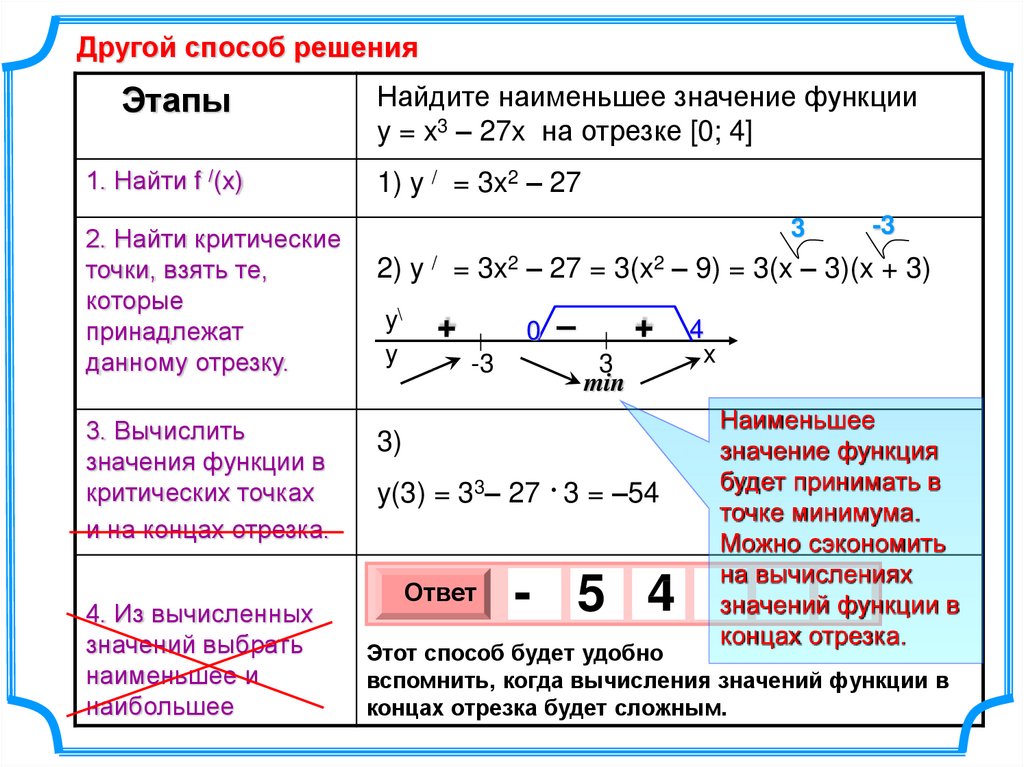
Другой способ решения
Этапы
1. Найти f /(x)
2. Найти критические
точки, взять те,
которые
принадлежат
данному отрезку.
3. Вычислить
значения функции в
критических точках
и на концах отрезка.
4. Из вычисленных
значений выбрать
наименьшее и
наибольшее
Найдите наименьшее значение функции
y = x3 – 27x на отрезке [0; 4]
1) y / = 3x2 – 27
3
-3
2) y / = 3x2 – 27 = 3(x2 – 9) = 3(x – 3)(x + 3)
y\
y
+
0
-3
–
+
3
min
4
x
3)
y(3) = 33– 27 3 = –54
Ответ
- 5 4
3
1 0
Наименьшее
значение функция
будет принимать в
точке минимума.
Можно сэкономить
на вычислениях
х
х
значений функции в
концах отрезка.
Этот способ будет удобно
вспомнить, когда вычисления значений функции в
концах отрезка будет сложным.

8.

2. Найдите наибольшее значение функции y = x3 – 3x + 4
на отрезке [– 2; 0]
Значения функции в
концах отрезка.
1) y(0) = 4
y(-2) = (-2)3– 3 (-2) +4 = 2
-1
1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
2) y / = 3x2 – 3 = 3(x2 – 1) = 3(x – 1)(x + 1)
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
y(-1) = (-1)3– 3 (-1) + 4 = 6
Выбрать наибольшее из
полученных значений.
x = 1 [-2; 0]
x = –1 [-2; 0]
Ответ
6
3
1 0 х
х

9.

3. Найдите наименьшее значение функции y = x3 – 2x2 + x +3
на отрезке [ 1; 4 ]
Значения функции в
концах отрезка.
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
1) y(1) = 1 – 2 + 1 + 3 = 3
y(4) = 43– 2 42 + 4 + 3 = 39
2) y / = 3x2 – 4x + 1= 3(x – 1)(x – 1 )
3
3x2 – 4x + 1 = 0
D=16–4*3*1=4
4+2
x1=
= 1 [1; 4]
6
4-2
1
= [1; 4]
x2=
6
3
y(1) = 3
Ответ
3
3
1 0 х
х

10.

x3
9x 7
4. Найдите наибольшее значение функции y
3
на отрезке [ -3; 3 ]
3
( 3)
Значения функции в
у ( 3)
9( 3) 7 9 27 7 11
концах отрезка.
3
33
у (3) 9 3 7 9 27 7 25
3
2
Найдем критические
3
х
точки, которые
у/
9 х 2 9 ( х 3)( х 3)
3
принадлежат
заданному отрезку.
x = 3 [-3; 3]
x = –3 [-3; 3]
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
y(-3) = 11
y(-3) = -25
В 11
1 1
3
10 х
х

11.

5. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
3
2
y x 3x 1
у(1) 1 3 1 1 1 3 1 1
3
2 2
у (9) 9 3 9 1 (3 ) 27 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
3
х 3 0
3
3
/
у х 3
х 3 2
2
2
3 х 6 0
1
2
х 2
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
Выбрать наибольшее из
полученных значений.
Ответ
1
3
1 0 х
х
2

12.

6. Найдите наименьшее значение функции y x х 3 x 1
3
на отрезке [ 1; 9 ]
Значения функции в
концах отрезка.
3
2
3
2
y x 2 31x 1
х 21 3
x 1 1 1
у(1) 1 3y
1 x1
3
2 2
у (9) 9 3 9 13 (3 ) 27 1
y х 2 3x 1
27 27 1 1
Найдем критические
точки, которые
принадлежат
заданному отрезку.
1
Запишем функцию
3 в удобном
х 3 виде
0 2
для дифференцирования
3 2
3
/
у х 3
х 3 2
2
2
3 х 6 0
х 2
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наименьшее из
полученных значений.
х 4 [1; 9]
3
2
3
2 2
у (4) 4 3 4 1 (2 ) 12 1
8 12 1 3
Ответ
-
3
3
1 0
х
х

13.

8. Найдите наибольшее значение функции
на отрезке [ 1; 9 ]
1
Значения функции в
концах отрезка.
/
1
1
2
х
х
Найдем критические
точки, которые
принадлежат
заданному отрезку.
Значения функции в
критических точках,
которые принадлежат
заданному отрезку.
Выбрать наибольшее из
полученных значений.
36
y х
х
ООФ: x = 0
y x 36
х
1
у (1) Запишем
1 36 функцию
37
в удобном
1
для дифференцирования
виде
1
у (9) 9 36 9 4 13
9
36 х 2 36
1
/
у 1 36 2 1 2
2
х
х
х
( х 6)( х 6)
x = 6 [ 1; 9]
х2
x = –6 [ 1; 9]
x = 0 D(y)
1
у (6) 6 36 6 6 12
6
Ответ
3 7
3
1 0 х
х

14.

(cosx) – sinx
/
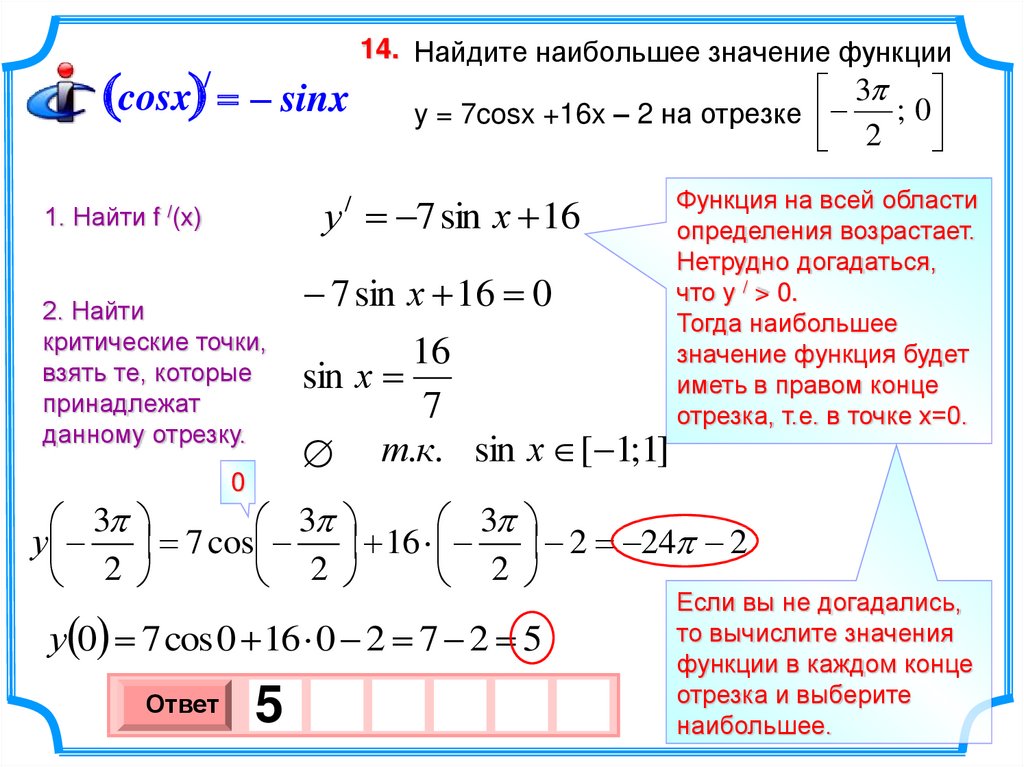
14. Найдите наибольшее значение функции
3
; 0
y = 7cosx +16x – 2 на отрезке
2
у 7 sin х 16
/
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
0
7 sin х 16 0
16
sin х
7
т.к. sin х [ 1;1]
Функция на всей области
определения возрастает.
Нетрудно догадаться,
что у / > 0.
Тогда наибольшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
3
3
3
у
7 cos
16
2 24 2
2
2
2
у(0) 7 cos 0 16 0 2 7 2 5
Ответ
5
3
1 0 х
х
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наибольшее.

15.

(sinx ) cosx
15. Найдите наибольшее значение функции
/
y = 10sinx –
у 10 cos х
/
1. Найти f
/(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
10 cos х
36
36
36
5
; 0
x + 7 на отрезке
6
Критических точек нет.
Тогда наибольшее
значение функция будет
принимать в одном из
концов отрезка.
36
cos х
10
т.к. cos х [ 1;1]
Можно было и раньше
догадаться, что
наибольшее значение
будет именно в левом
конце отрезка!
Как?
1
5
5 36 5
у
10 sin
7 10 30 7 32
2
6
6 6
Синус –нечетная функция
0
Формула приведения
5
5
1
(
)
у 0 sin
10 sin
7 7 Ответ
0 0
sin
sin sin
3 2
6
6
6
3
1 0 х
х
6
2

16.

(cosx) – sinx
16. Найдите наименьшее значение функции
/
у / 5 sin x 6
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
3
у
2
y = 5cosx – 6x + 4 на отрезке
5 sin x 6 0
6
sin х
5
т.к. sin х [ 1;1]
0
3
5 cos
2
3
6
2
у(0) 5 cos 0 0 4 9
Ответ
9
3
1 0 х
Функция на всей области
определения убывает.
Нетрудно догадаться, что
у / < 0.
Тогда наименьшее
значение функция будет
иметь в правом конце
отрезка, т.е. в точке х=0.
4 9 4
1
х
3
2 ; 0
Если вы не догадались,
то вычислите значения
функции в каждом конце
отрезка и выберите
наименьшее.

17.

17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
3
sin х
2
х ( 1)
n
3
3
n
Но нам не нужны ВСЕ
у 12 cos 6 3 2 3 6
12
стационарные
точки.
3
3
3
Необходимо сделать выбор тех
значений, которые попадут в
заданный отрезок
у 12 cos 6 3 2 3 6 6 3 0 ;
2
2
2
у (0) 12 cos 0 6 3 0 2 3 6 18 2 3
Ответ
1 2
3
1 0 х
х
2

18.

17. Найдите наибольшее значение функции
y = 12cosx + 6 3 x – 2 3 + 6 на отрезке 0 ;
2
1. Найти f /(x)
у / 12 sin x 6 3
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
12 sin x 6 3 0
y\
y
0
3
sin х
2
+
–
2
x
3
max
3
Убедимся, что данная точка
является точкой максимума на
заданном промежутке.
Значит, наибольшее значение
функция достигает именно в этой
точке.
Тогда значения функции в концах
отрезка можно не считать.
у 12 cos 6 3 2 3 6 12
3
3
3
Ответ
1 2
3
1 0 х
х

19.

18. Найдите наименьшее значение функции
7 3
14 3
7 3
y = 11 +
–
х–
cosx на отрезке 0 ;
2
18
3
3
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
y\
y
0
–
7 3 14 3
у
sin x
6
3
3
7 3 14 3
sin x 0
3
3
Можно убедиться, что данная
1
n
точка
является
точкой
х ( 1)
минимума
n
sin x
на заданном промежутке.
6
2
/
+
6 min
2
x
Значит, наименьшее значение
функция
достигает
именно в этой
Но нам не
нужны ВСЕ
точке.
стационарные точки.
Тогда
значения
функции
в концах
Необходимо
сделать
выбор
тех
отрезка
можно
не считать.
значений,
которые
попадут в
заданный отрезок
7 3 7 3 14 3
у 11
cos 11 7 4
18
18
3
6
6
В 11
4
0 ; 2
3
10 х
х

20.

(tgx)
/
19. Найдите наименьшее значение функции
1
cos2x y = 4tgx – 4x – 4 + 5 на отрезке 4 ; 4
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 4
4
2
cos x
/
4
0
4
4 0
2
cos x
cos 2 x 1
Нам не нужны ВСЕ
у 4 5 1
4
у 4 5 9 2
4
у(0) 0 0 5 5
Ответ
4
стационарные точки.
Необходимо сделать выбор тех
значений, которые попадут в
3. Вычислим
значения функции
заданный
отрезок
в критических точках
;
и на концах отрезка.
4 4
4. Из вычисленных значений
сделаем выбор наименьшего.
1
3
1 0 х
х

21.

(tgx)
/
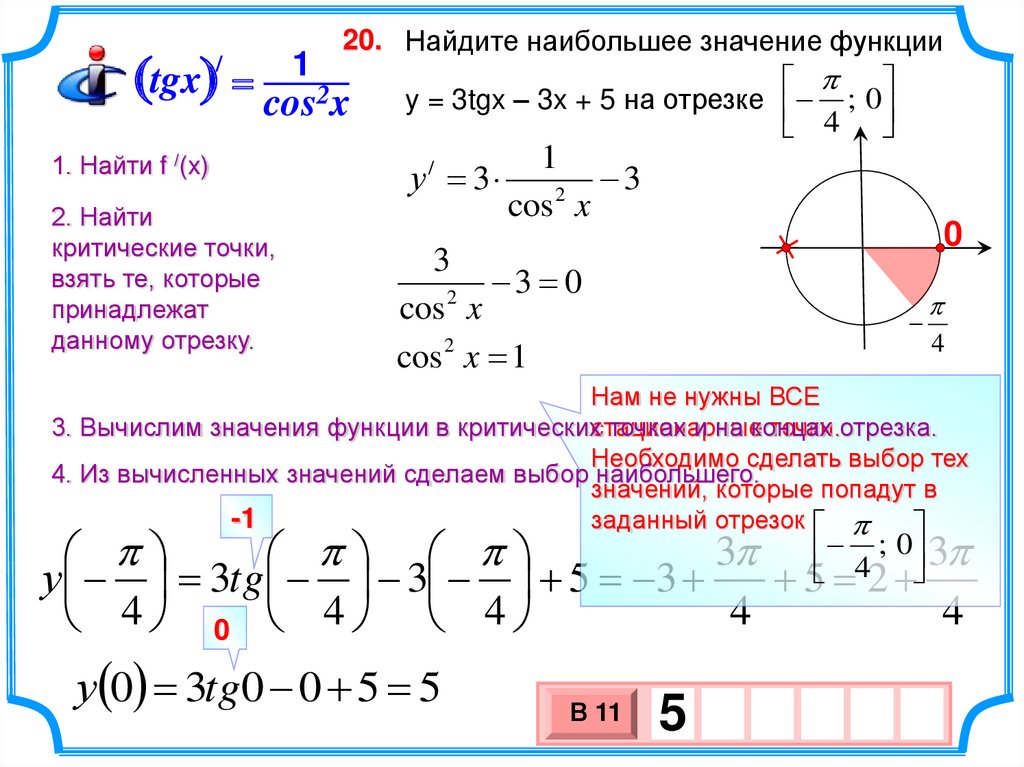
20. Найдите наибольшее значение функции
1
2
cos x y = 3tgx – 3x + 5 на отрезке 4 ; 0
1. Найти f /(x)
2. Найти
критические точки,
взять те, которые
принадлежат
данному отрезку.
1
у 3
3
2
cos x
/
0
3
3 0
2
cos x
cos 2 x 1
4
Нам не нужны ВСЕ
3. Вычислим значения функции в критическихстационарные
точках и на концах
точки.отрезка.
Необходимо сделать выбор тех
4. Из вычисленных значений сделаем выбор наибольшего.
значений, которые попадут в
-1
заданный отрезок
3 4 ; 0 3
у 3tg 3 5 3
5 2
4
4
4 0 4 4
у(0) 3tg0 0 5 5
В 11
5
3
10 х
х