Similar presentations:
Вписанная в треугольник окружность
1.
2.
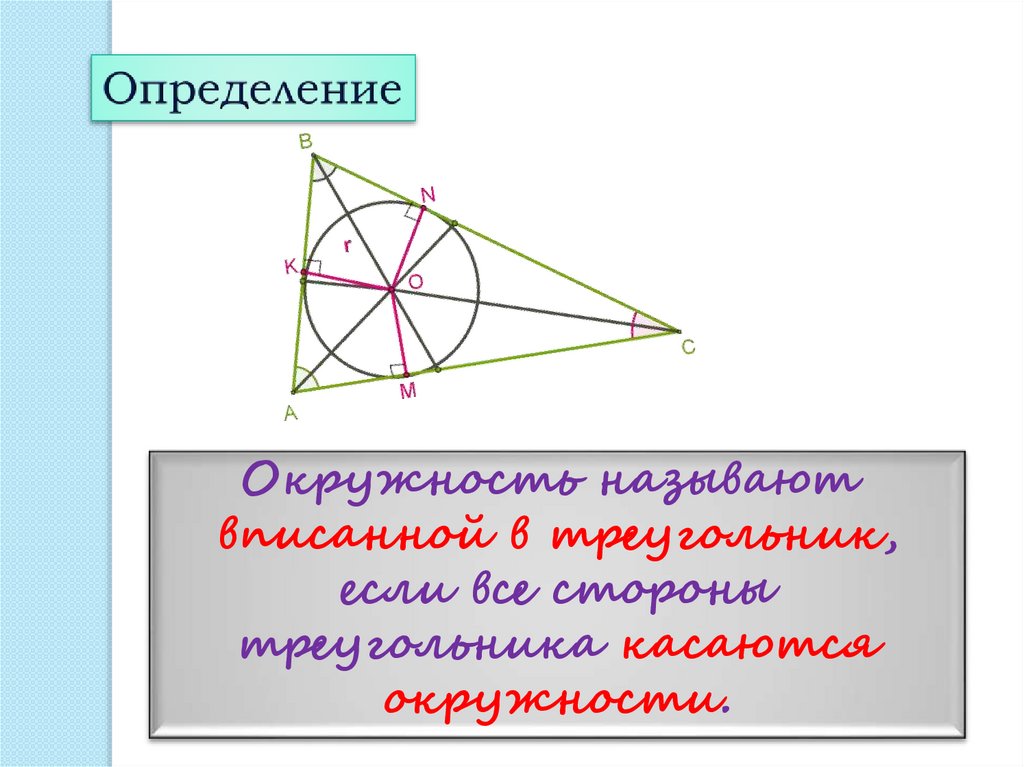
Окружность называютвписанной в треугольник,
если все стороны
треугольника касаются
окружности.
3.
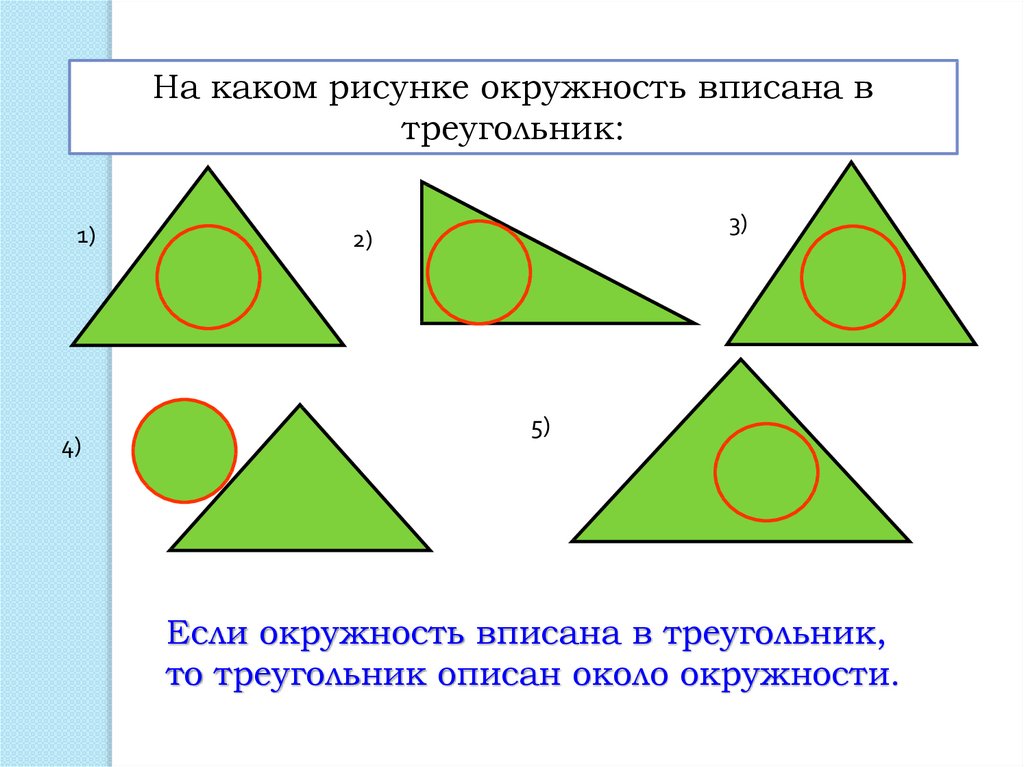
На каком рисунке окружность вписана втреугольник:
1)
4)
3)
2)
5)
Если окружность вписана в треугольник,
то треугольник описан около окружности.
4.
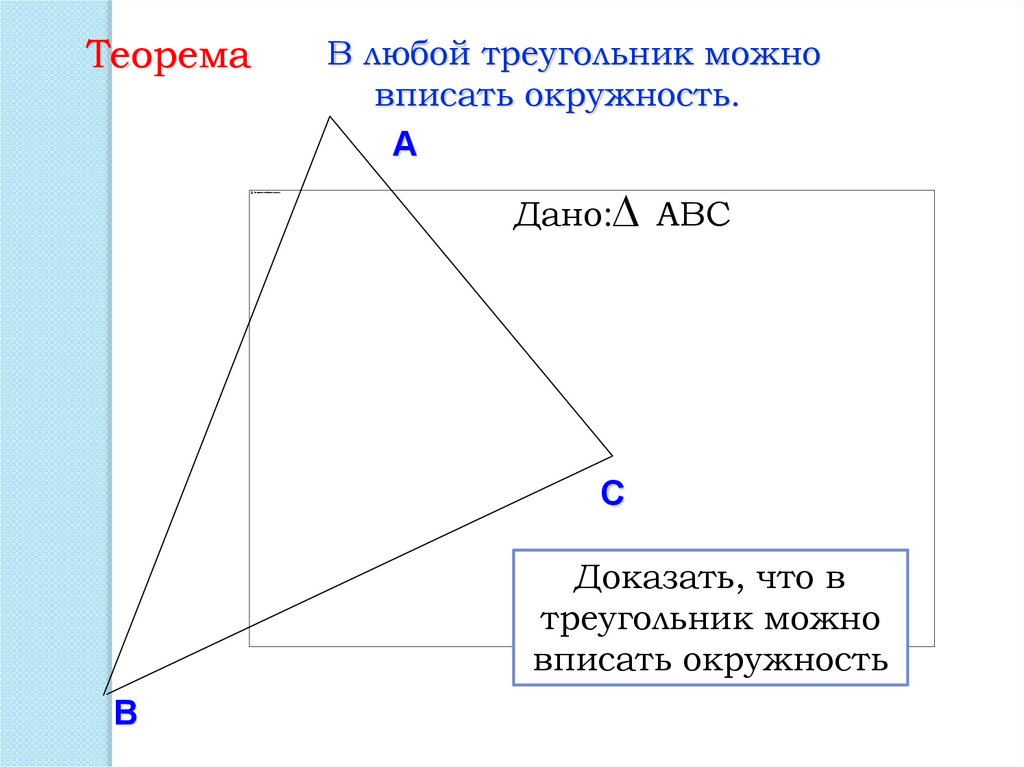
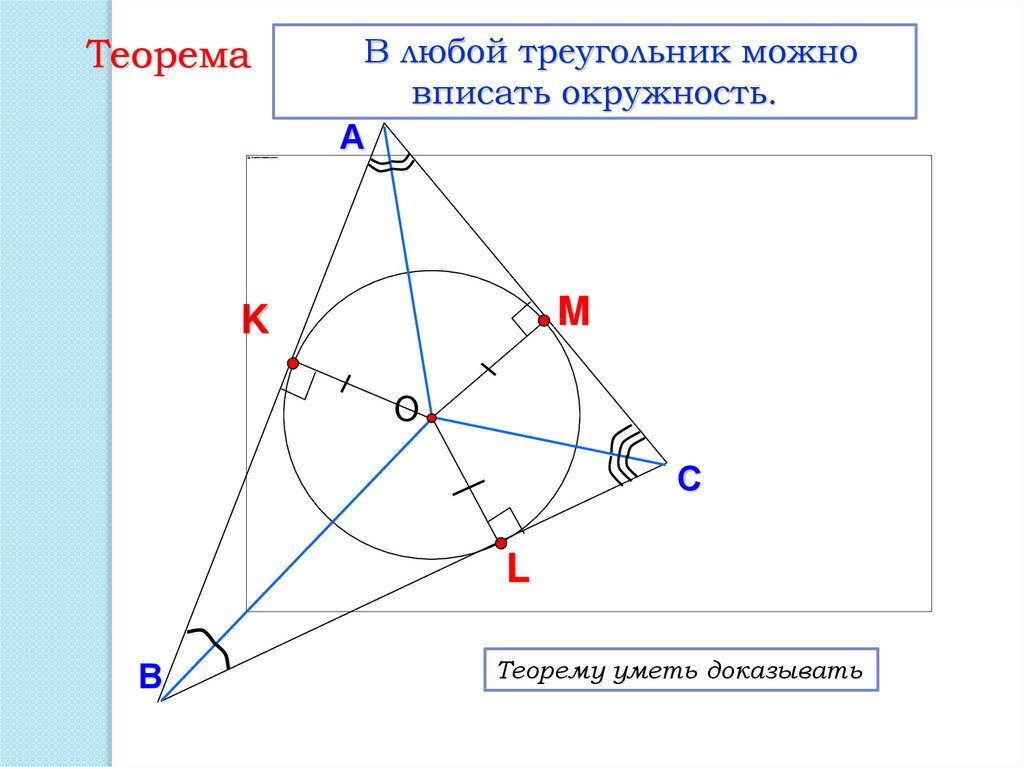
ТеоремаВ любой треугольник можно
вписать окружность.
А
Дано: АВС
С
Доказать, что в
треугольник можно
вписать окружность
В
5.
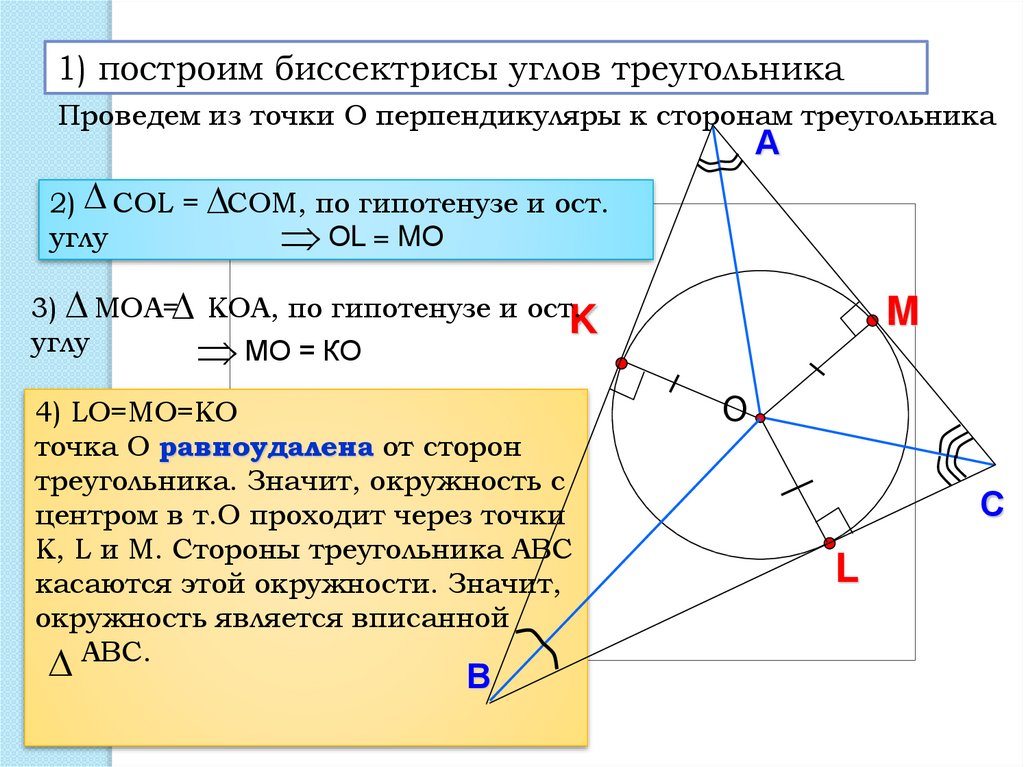
1) построим биссектрисы углов треугольникаПроведем из точки О перпендикуляры к сторонам треугольника
А
2) СOL = COМ, по гипотенузе и ост.
углу
ОL = MО
3) МОА= КОА, по гипотенузе и ост.
K
углу
МО = КО
4) LО=MО=KО
точка О равноудалена от сторон
треугольника. Значит, окружность с
центром в т.О проходит через точки
K, L и M. Стороны треугольника АВС
касаются этой окружности. Значит,
окружность является вписанной
АВС.
В
M
О
С
L
6.
ТеоремаВ любой треугольник можно
вписать окружность.
А
M
K
О
С
L
В
Теорему уметь доказывать
7. Следствие 1
ВА
r
О
r
r
С
Дано: Окр.(О;r) вписана в
ОВ,ОС,ОА - биссектрисы
АВС.
8.
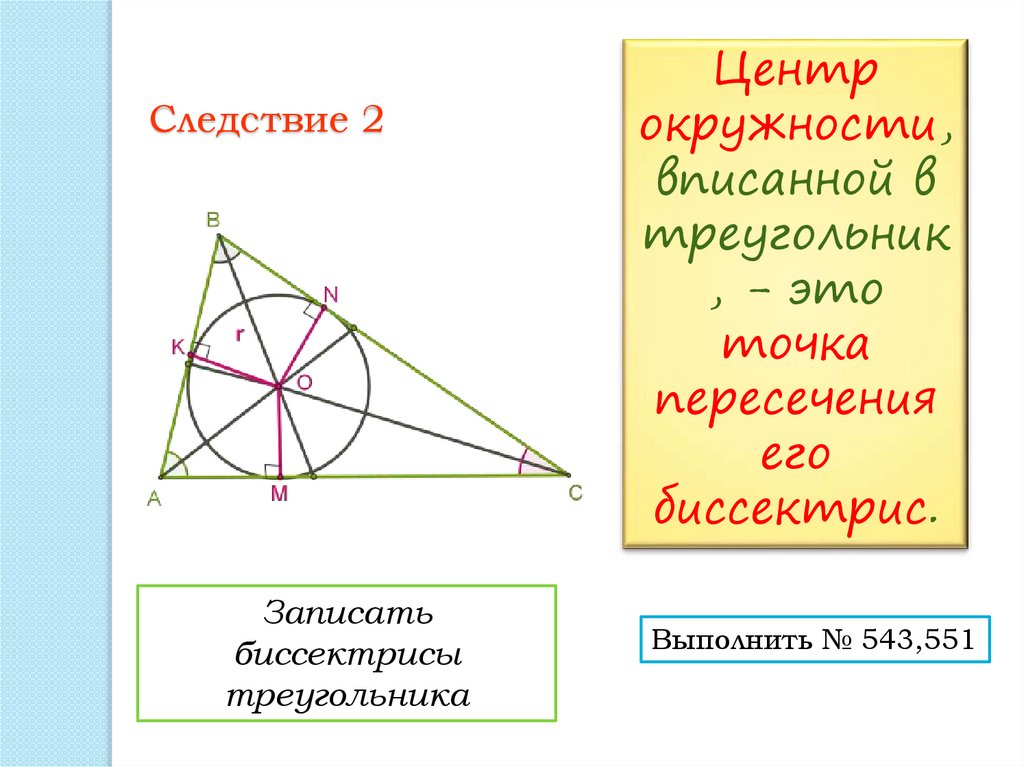
Следствие 2Записать
биссектрисы
треугольника
Центр
окружности,
вписанной в
треугольник
, - это
точка
пересечения
его
биссектрис.
Выполнить № 543,551
9.
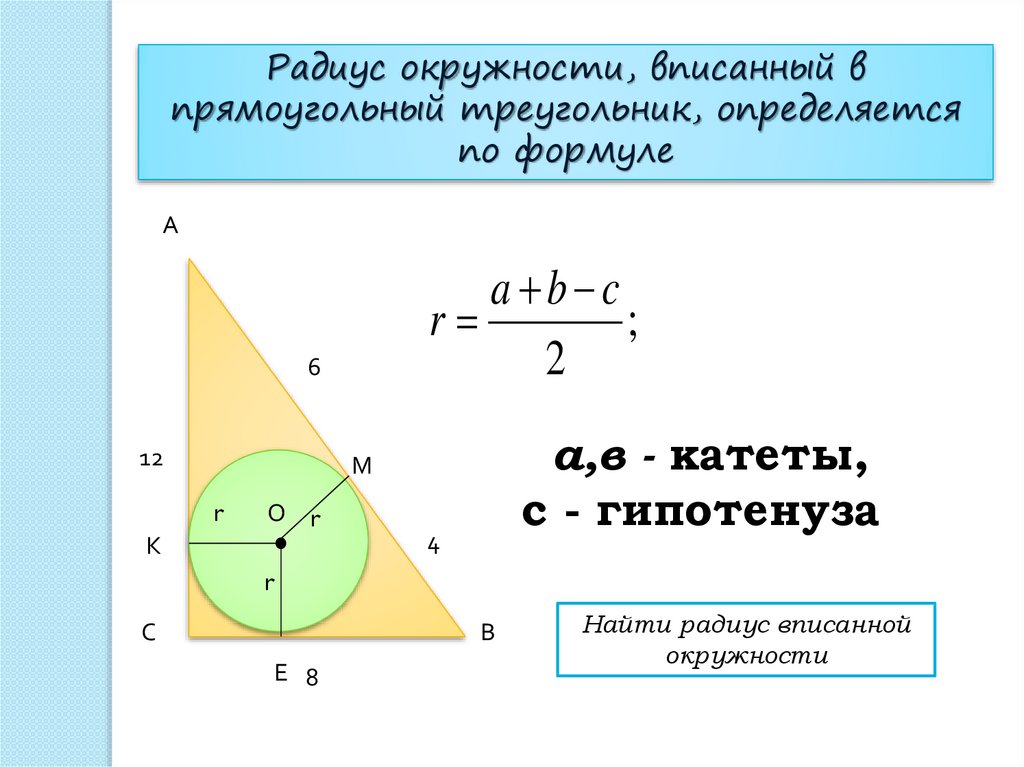
Радиус окружности, вписанный впрямоугольный треугольник, определяется
по формуле
А
a b c
r
; a, b
2
6
12
а,в - катеты,
с - гипотенуза
М
r
О r
К
4
r
С
В
Е 8
Найти радиус вписанной
окружности



 mathematics
mathematics








