Similar presentations:
Формула разности квадратов
1. Формула разности квадратов.
2.
Прочитайте выраженияa–b
разность чисел а и b
a+b
сумма чисел а и b
(a + b)(a – b)
произведение суммы и
разности чисел а и b
a2 – b2
разность квадратов чисел а и
b
квадрат разности чисел а и b
(a – b)2
3. Найдите квадрат чисел
34a
9
16а2
1
3
mn
0,6b
1
9
m2n2
0,36b2
4. Представьте в виде квадрата одночлена:
9b216m4
0,09x10
0,81m2n2
x4y6
(3b)2
(4m2)2
(0,3x5)2
(0,9mn)2
(x2y3)2
5. Разложите на множители
2а – 4ab – b2
a2 – b2
2(а – 2)
b(а – b)
?
6. Тема урока
«Разность квадратов»7. Перемножьте два многочлена:
(a+b)(a – b)(3x – 2y)(3x+2y)
1 1
1
1
m n m n
3 4
3
4
8.
(a+b)(a-b) = a2 – ab + ab -b2 = a2 -b2(3x-2y)(3x+2y) = 9x2 – 6xy + 6xy – 4y2 =9x2– 4y2
1 1
1 1 2 1
1
1 2 1 2 1 2
1
m n m n m mn mn n m n
3 4
3 16
12
12
9
16
9
4
9. a2 – b2 = (а – b)(а + b)
2a –
2
b = (а
– b)(а + b)
Если мы будем на нее смотреть справа налево,
то получим сокращенное (короткое)
умножение многочленов,
а если слева на право - представление разности
квадратов в виде произведения (в дальнейшем
это будем называть разложение на множители).
10.
Выберите выражение, которыемогут быть преобразованы по
формуле a2 – b2 = (а – b)(а + b)
а) (5+2)(5-2)
б) (a – b)-(a+b)
в) (x – y)(x+y)
г) (0,5 – m)(0,5+m)
д) 2
2
а а
3
3
а, в, г, д
11.
(4a – 7)(4a + 7) = 16a2 – 49...
9m2
(x – 3 m) (x + 3m) = x2 – ...
(0,4 – 0,3a)(0,4 + 0,3a) =0,16
... – 0,9a2
(mn – b) (mn + b) =m2...n2 – b2
12. Д/з: №855, 857
Работа с учебником:№854, 859
Д/з: №855, 857







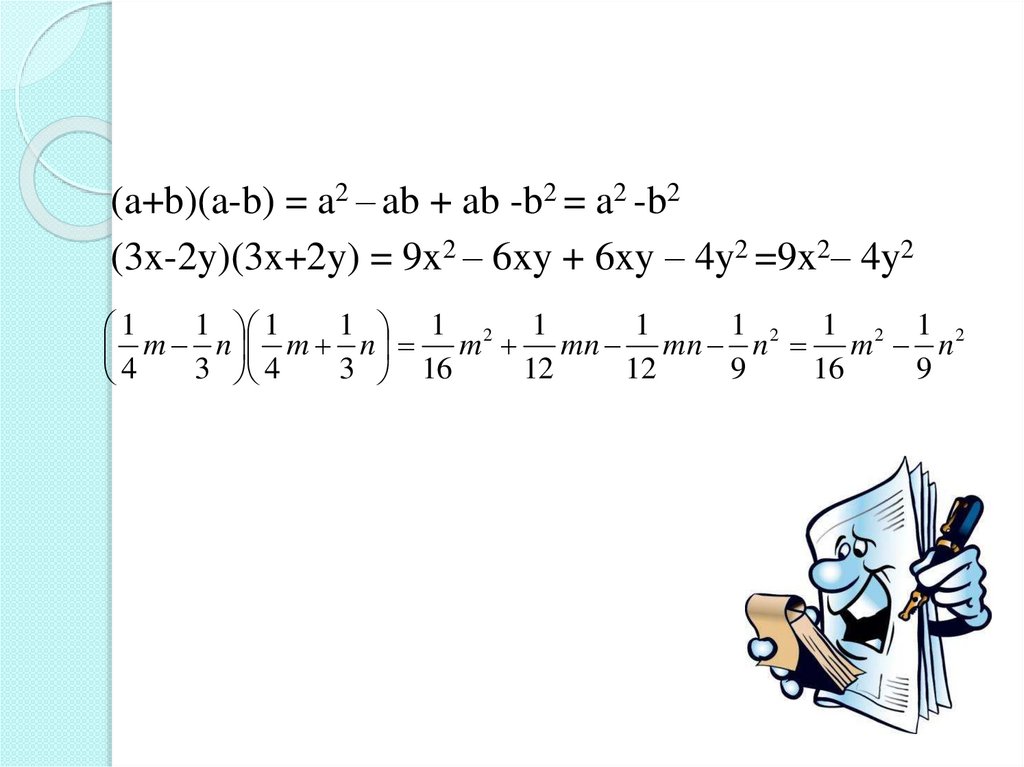


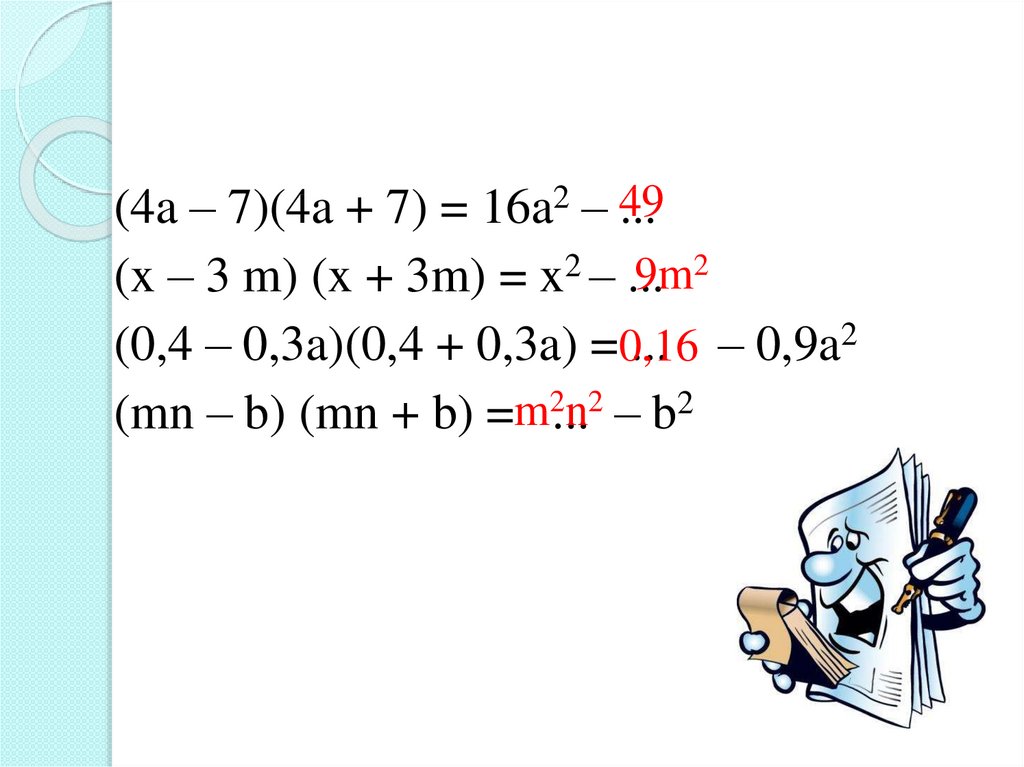

 mathematics
mathematics








