«Прямоугольный треугольник». Тренажер. 8 класс

1. Тренажер по теме «Прямоугольный треугольник»

2.

Подготовка к ЕГЭ (В-4).
ПОМНИТЕ!
Не забывайте делать проверку!

3.

А
С
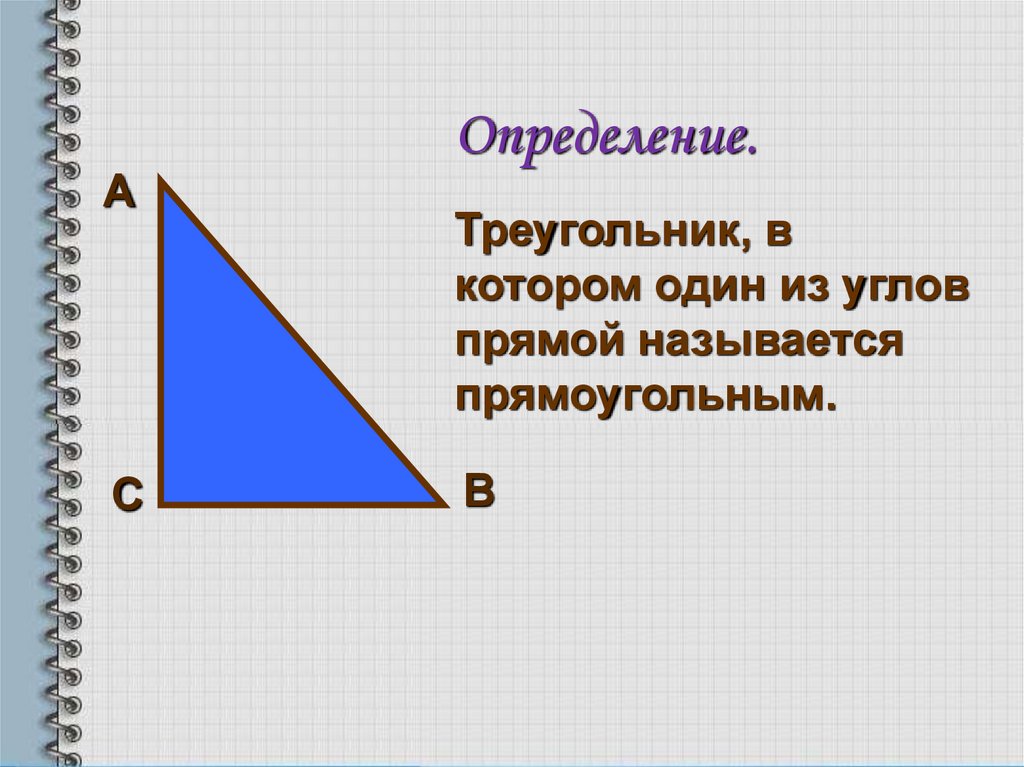
Определение.
Треугольник, в
котором один из углов
прямой называется
прямоугольным.
В

4.

катет
А
С катет В
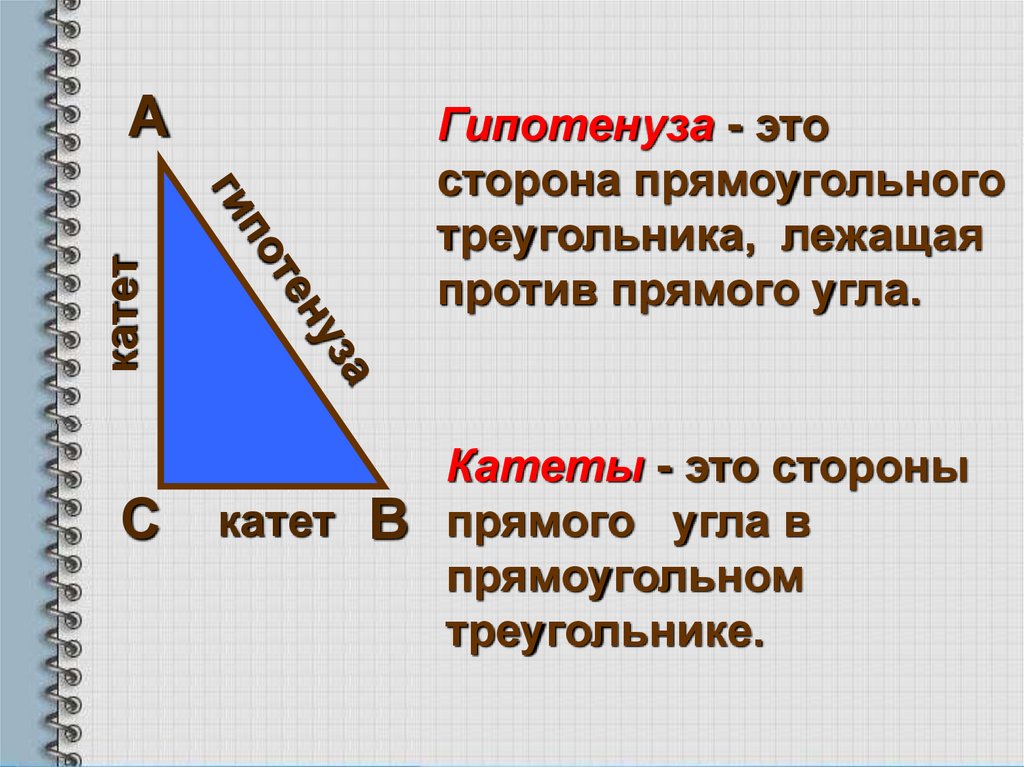
Гипотенуза - это
сторона прямоугольного
треугольника, лежащая
против прямого угла.
Катеты - это стороны
прямого угла в
прямоугольном
треугольнике.

5.

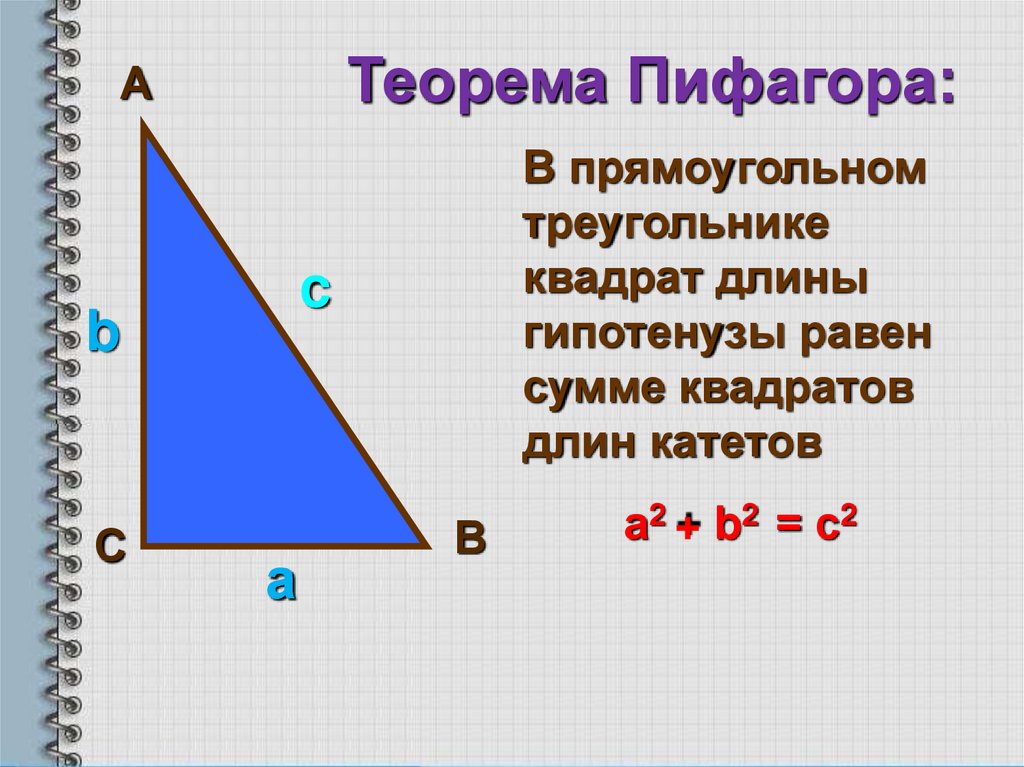
Теорема Пифагора:
А
c
b
С
В прямоугольном
треугольнике
квадрат длины
гипотенузы равен
сумме квадратов
длин катетов
а
В
а2 + b2 = с2

6.

Определение.
А
С
Косинусом острого
угла прямоугольного
треугольника
называется отношение
прилежащего катета к
гипотенузе.
В
соs А = AС/AВ
соs В = ВС/AВ

7.

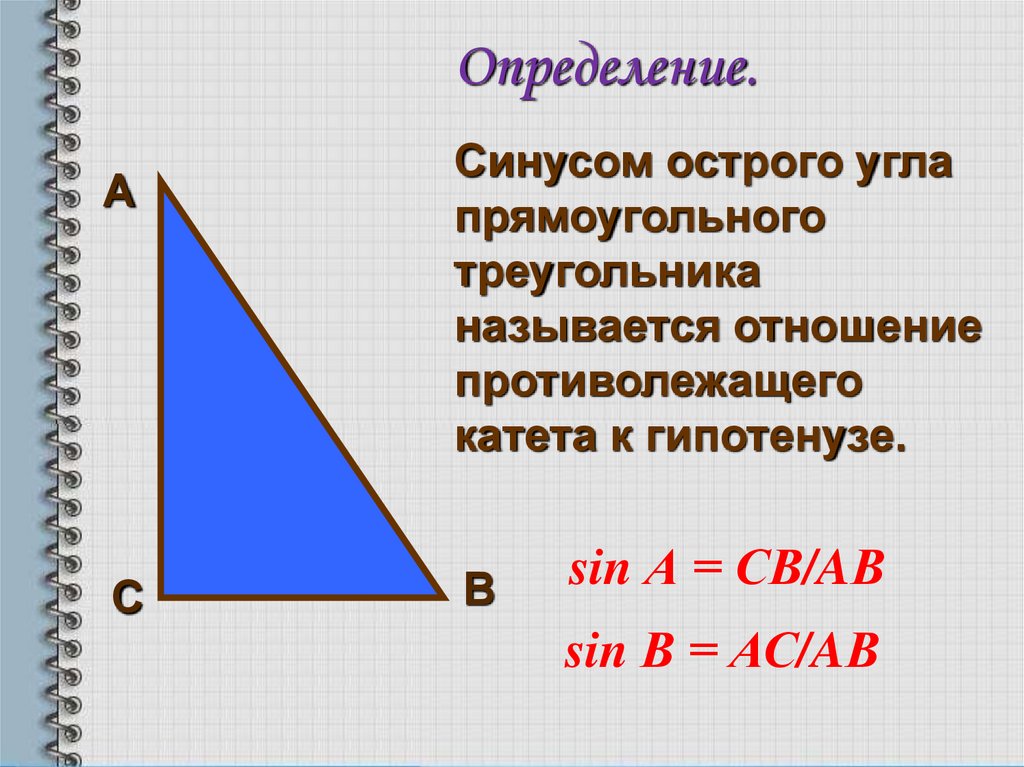
Определение.
А
С
Синусом острого угла
прямоугольного
треугольника
называется отношение
противолежащего
катета к гипотенузе.
В
sin А = СВ/AВ
sin В = АС/AВ

8.

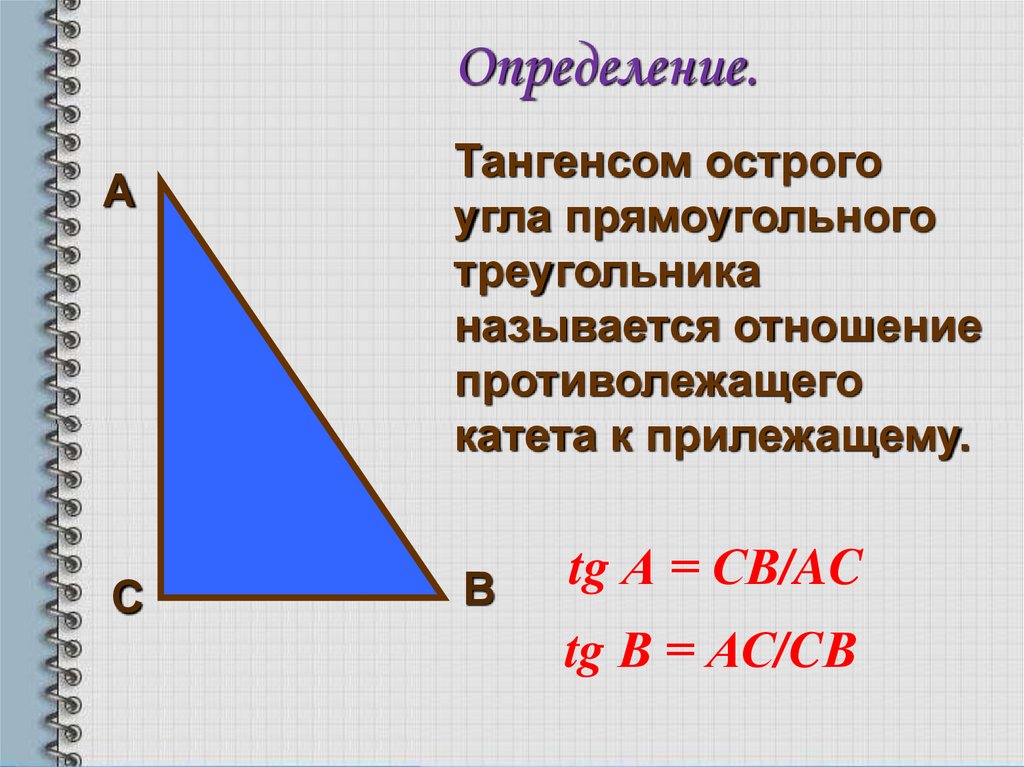
Определение.
А
С
Тангенсом острого
угла прямоугольного
треугольника
называется отношение
противолежащего
катета к прилежащему.
В
tg А = СВ/AC
tg В = АС/CВ

9. Вариант 1

ПРОВЕРКА
Вариант 2
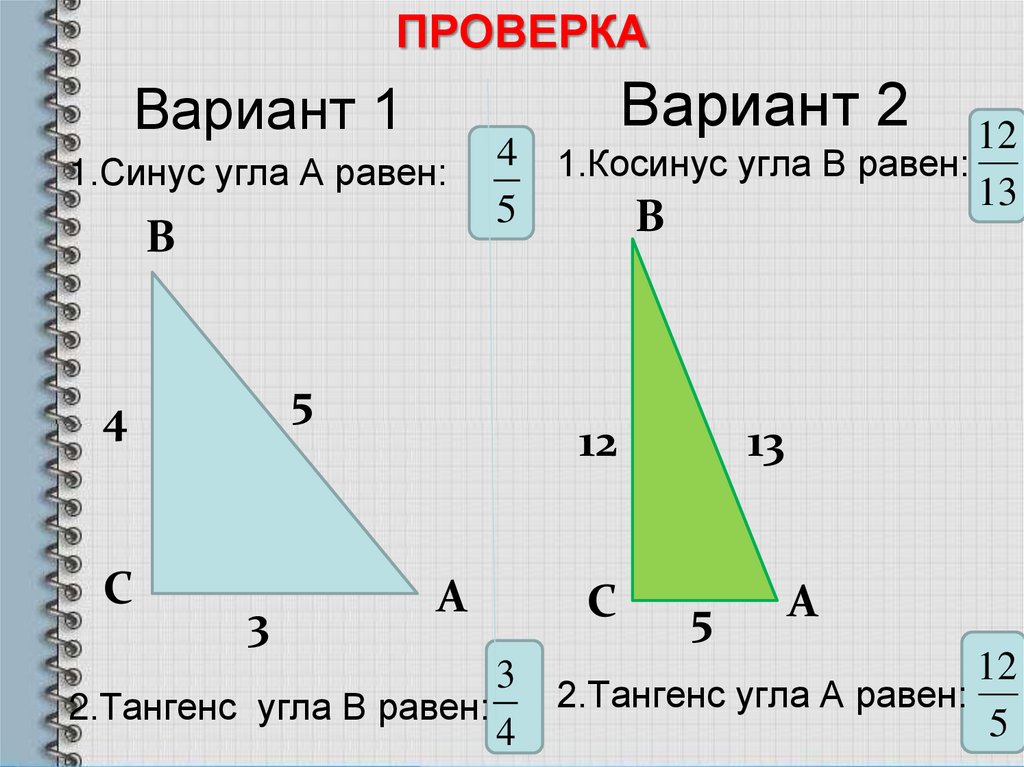
Вариант 1
1.Синус угла А равен:
В
5
4
С
4 1.Косинус угла В равен: 12
13
5
В
3
12
А
3
2.Тангенс угла В равен:
4
С
13
5
А
12
2.Тангенс угла А равен:
5

10. Пример 1.

• В треугольнике ABC угол C равен 90° , AB = 30,
AC = 3 √19 . Найдите sin A.
Решение:
А
С
АВ2 = АС2 + ВС2 (по
теореме Пифагора)
ВС2 = 900 – 171 = 729
ВС = 27
sin А = ВС/AВ = 27/30 = 0,9
В

11. Пример 2.

• В
равнобедренном
треугольнике
ABC
с
основанием AC боковая сторона AB равна 10, а
высота, проведенная к основанию, равна 2√ 21.
Найдите косинус угла А.
Решение:
В
6
А
Е
В треугольнике АВЕ
АВ2 = АЕ2 + ВЕ2 (по теореме
Пифагора)
АЕ2 = 100 – 84 = 16
АЕ = 4
соs А = AЕ/AВ = 4/10 = 0,4
С

12. Пример 3.

• В равнобедренном треугольнике ABC с основанием
AC боковая сторона AB равна 17, а cos А = 8 /17 .
Найдите высоту, проведенную к основанию.
Решение:
В
6
А
Е
С
В треугольнике АВЕ
соs А = AЕ/AВ
8 /17 = АЕ/17
АЕ = 8
АВ2 = АЕ2 + ВЕ2 (по теореме
Пифагора)
ВЕ2 = 289 – 64 = 225
ВЕ = 15

13.

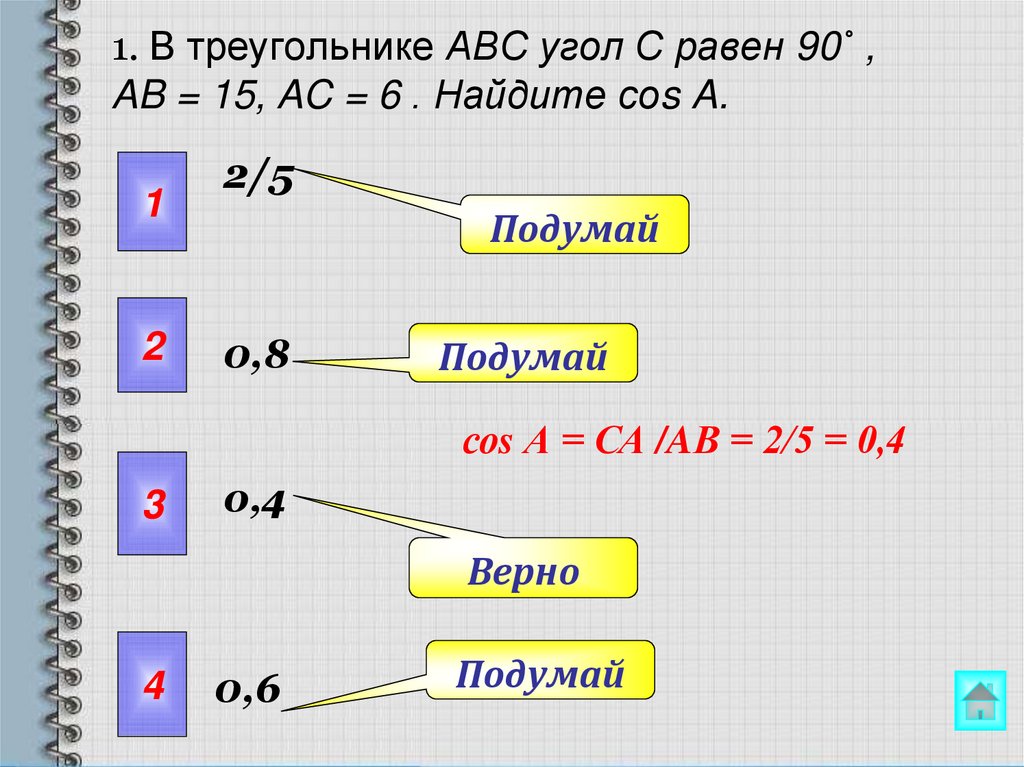
14. 1. В треугольнике ABC угол C равен 90˚ , AB = 15, AC = 6 . Найдите соs A.

1
2
2/5
Подумай
0,8
Подумай
соs А = СА /AВ = 2/5 = 0,4
3
0,4
Верно
4
0,6
Подумай

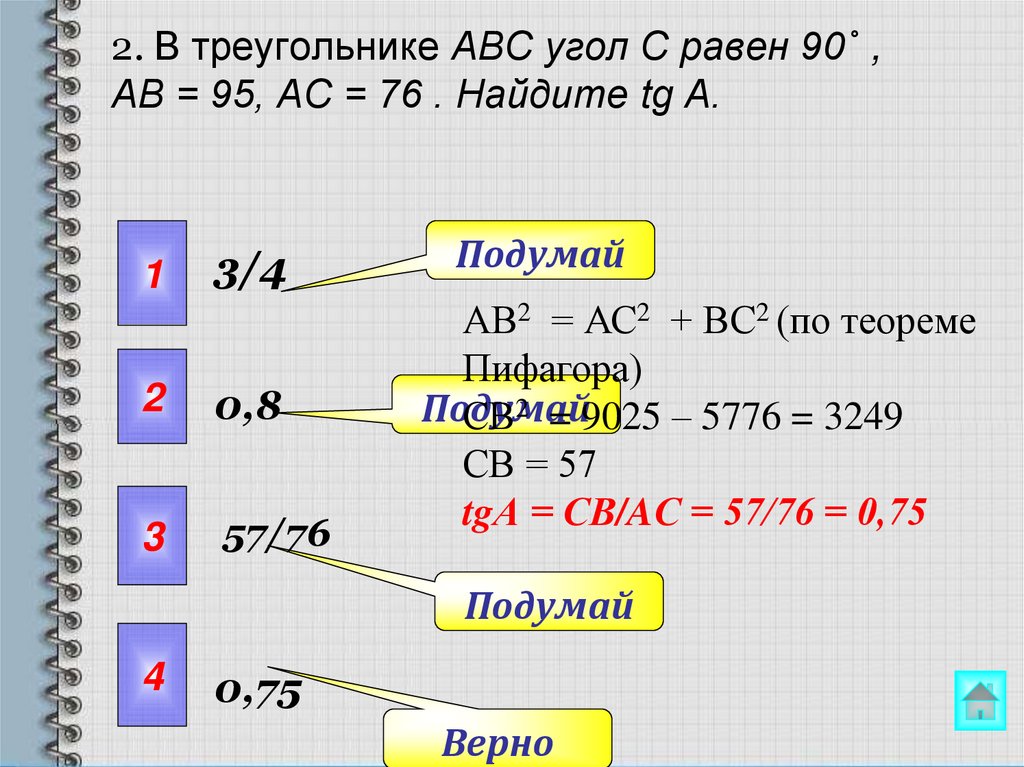
15. 2. В треугольнике ABC угол C равен 90˚ , AB = 95, AC = 76 . Найдите tg A.

1
3/4
2
0,8
3
57/76
Подумай
АВ2 = АС2 + ВС2 (по теореме
Пифагора)
Подумай
СВ2 = 9025 – 5776 = 3249
СВ = 57
tgА = СВ/AС = 57/76 = 0,75
Подумай
4
0,75
Верно

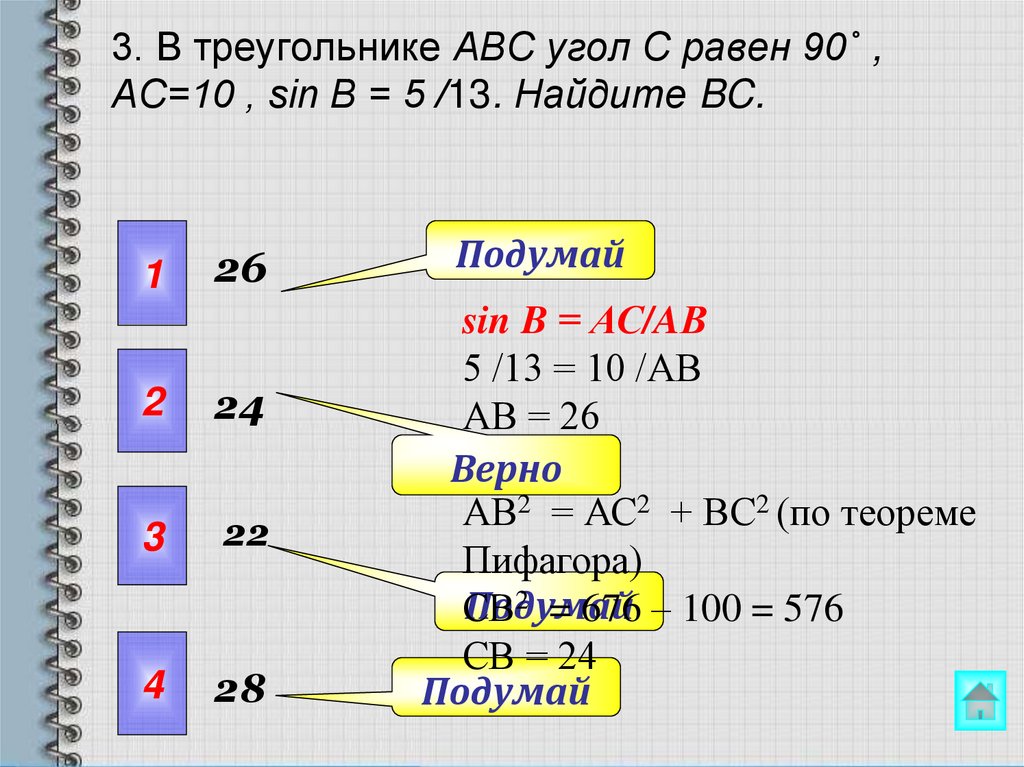
16. 3. В треугольнике ABC угол C равен 90˚ , AC=10 , sin В = 5 /13. Найдите BC.

1
26
2
24
3
22
4
28
Подумай
sin B = АС/AВ
5 /13 = 10 /АВ
АВ = 26
Верно
АВ2 = АС2 + ВС2 (по теореме
Пифагора)
2 = 676 – 100 = 576
Подумай
СВ
СВ = 24
Подумай

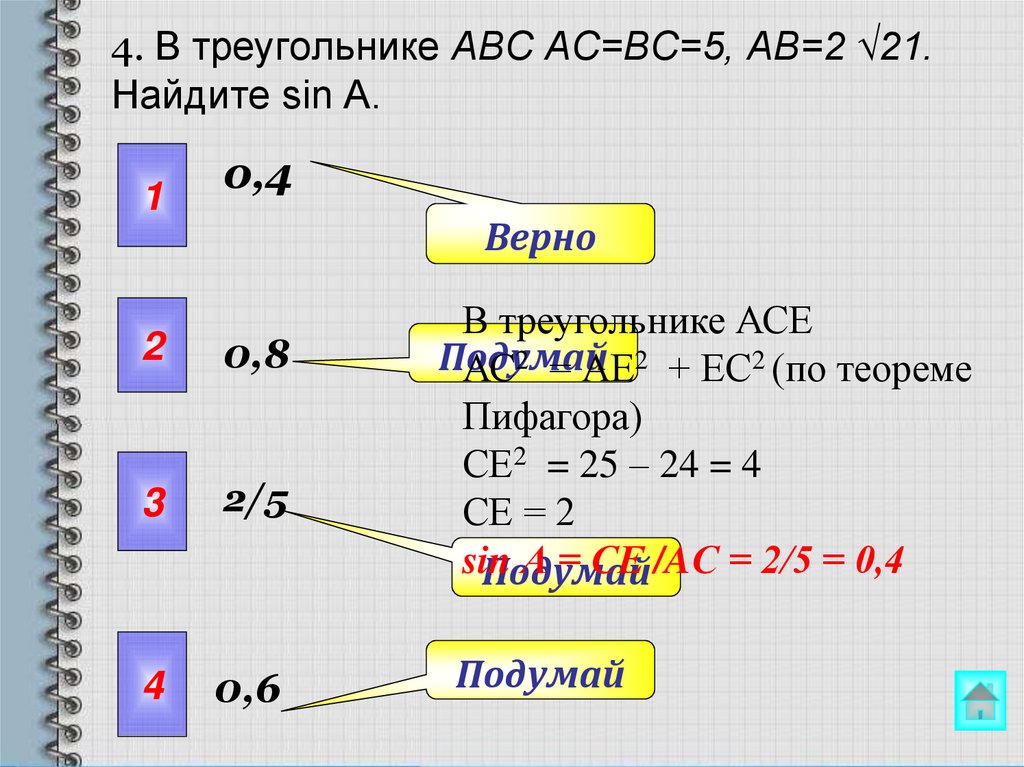
17. 4. В треугольнике ABC AC=BC=5, AB=2 √21. Найдите sin A.

1
0,4
Верно
2
0,8
3
2/5
4
0,6
В треугольнике АСЕ
Подумай
АС2 = АЕ2 + ЕС2 (по теореме
Пифагора)
СЕ2 = 25 – 24 = 4
СЕ = 2
sin
А = СЕ /AС = 2/5 = 0,4
Подумай
Подумай