Вписанная окружность

1.

2.

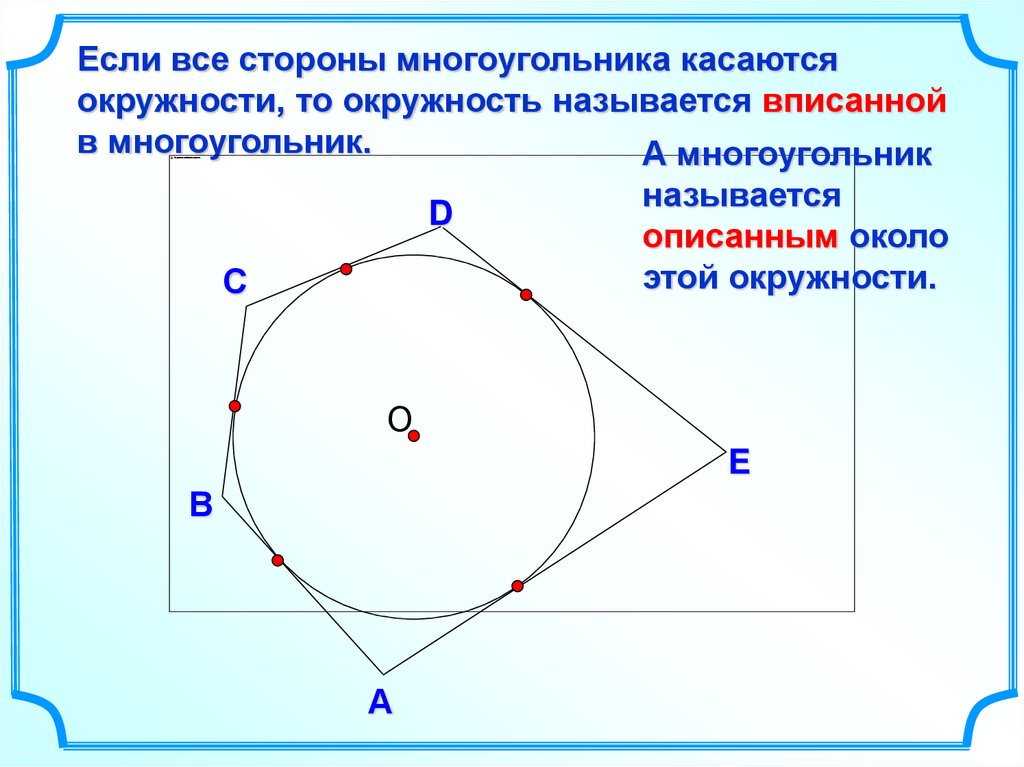
Если все стороны многоугольника касаются
окружности, то окружность называется вписанной
в многоугольник.
А многоугольник
D
С
называется
описанным около
этой окружности.
О
E
В
А

3.

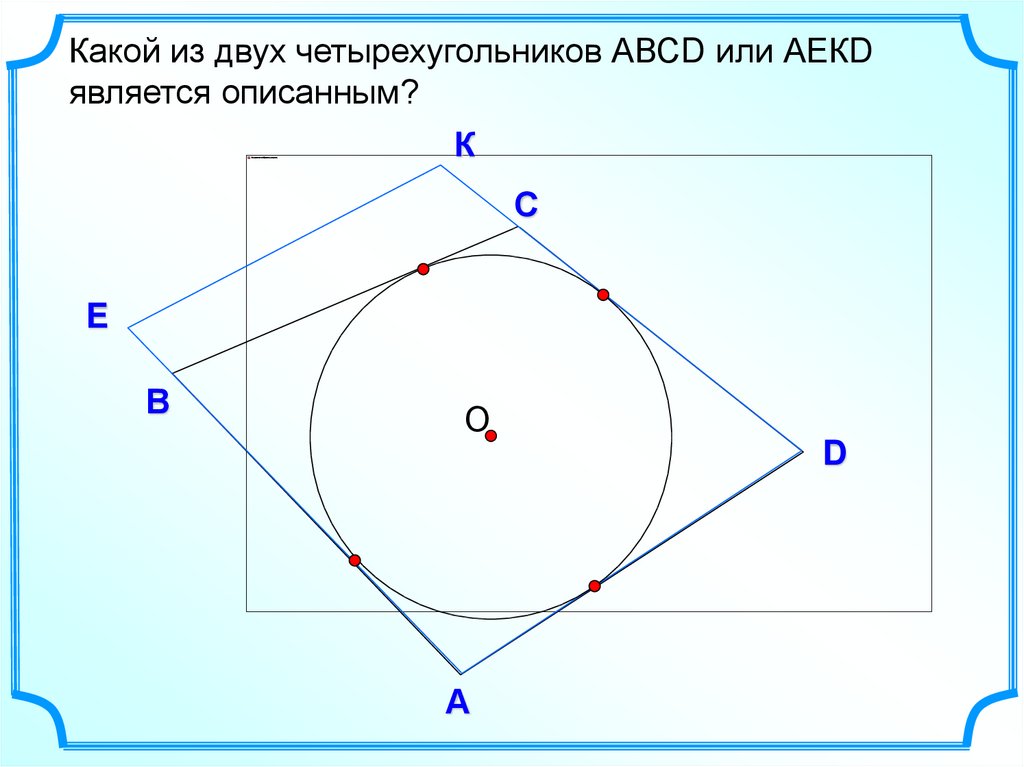
Какой из двух четырехугольников АВСD или АЕКD
является описанным?
К
С
E
В
О
D
А

4.

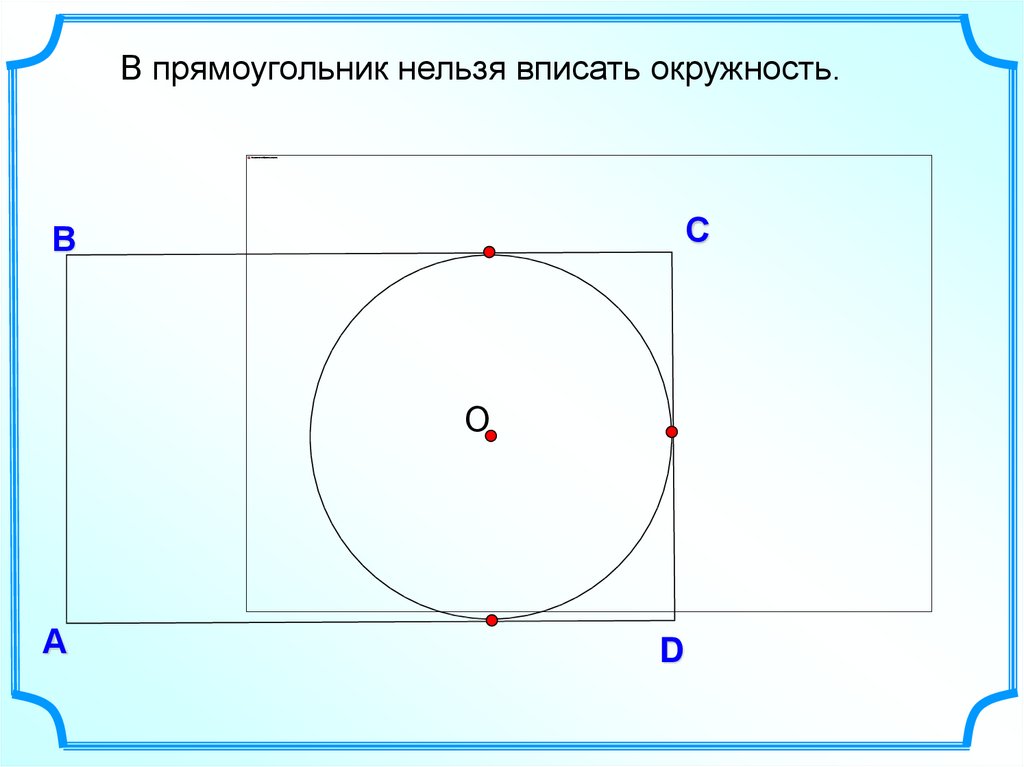
В прямоугольник нельзя вписать окружность.
С
В
О
А
D

5.

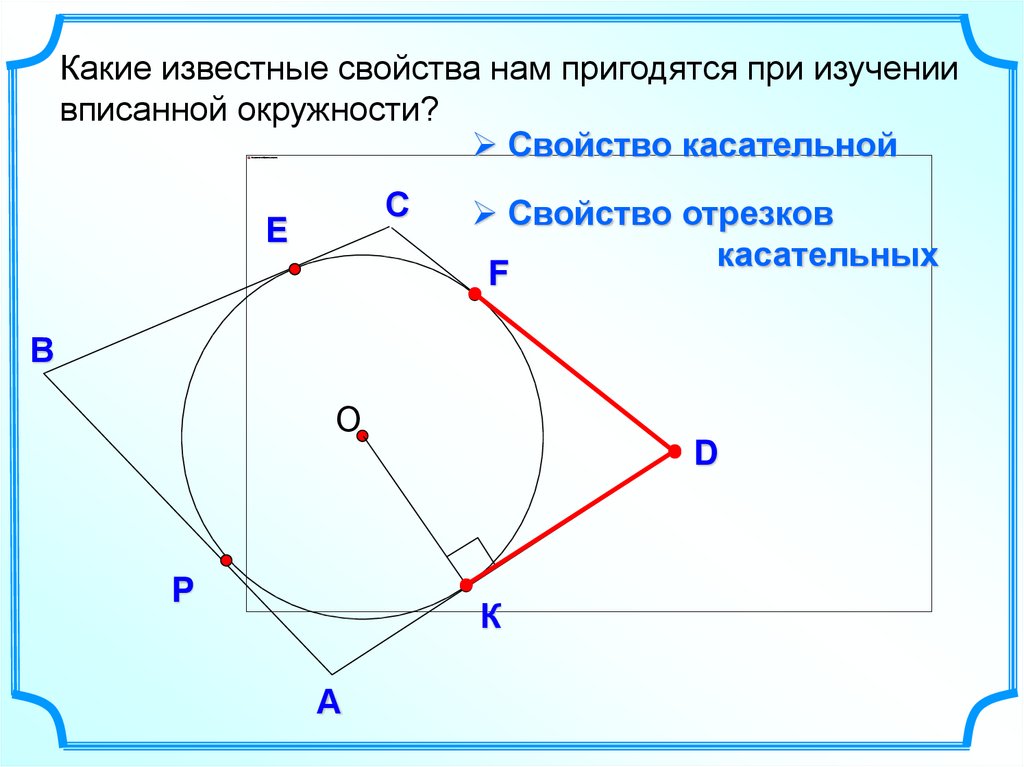
Какие известные свойства нам пригодятся при изучении
вписанной окружности?
Свойство касательной
С
E
Свойство отрезков
касательных
F
В
О
D
P
К
А

6.

В любой треугольник можно
вписать окружность.
Где находится её центр?
В правильный многоугольник
Можно вписать окружность.
Где лежит её центр?

7.

Теорема
А
В любой треугольник можно
вписать окружность.
Дано: АВС
Доказать, что в
треугольник можно
вписать окружность
С
В

8.

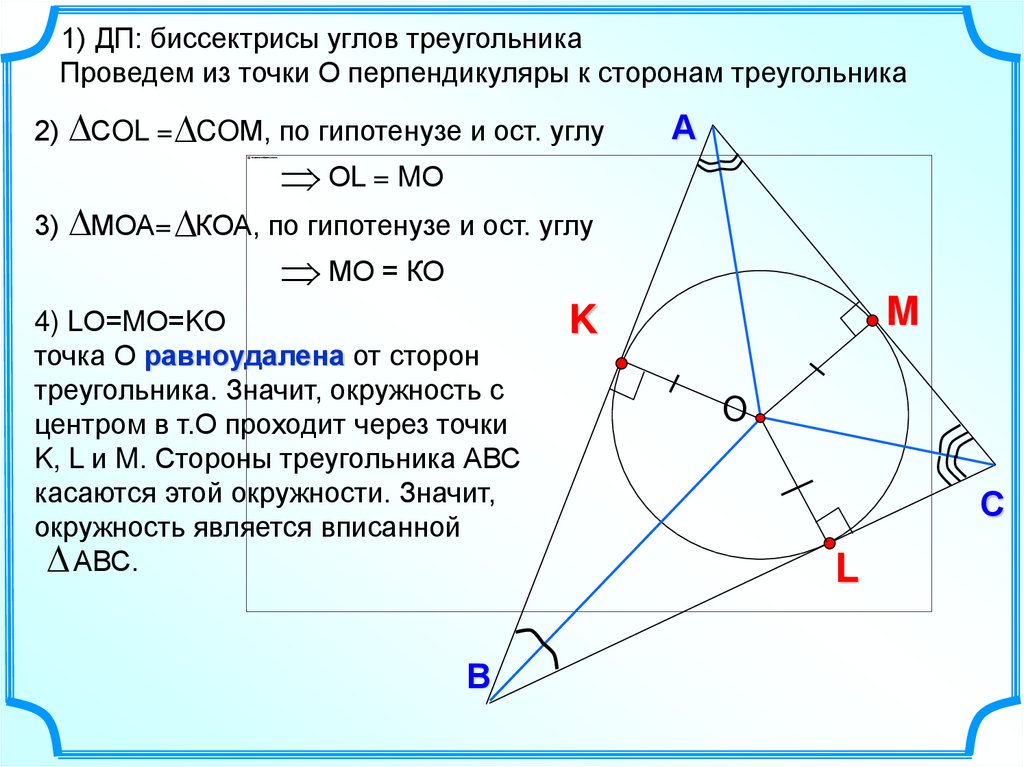
1) ДП: биссектрисы углов треугольника
Проведем из точки О перпендикуляры к сторонам треугольника
2)
СOL = COМ, по гипотенузе и ост. углу
А
ОL = MО
3)
МОА= КОА, по гипотенузе и ост. углу
МО = КО
4) LО=MО=KО
точка О равноудалена от сторон
треугольника. Значит, окружность с
центром в т.О проходит через точки
K, L и M. Стороны треугольника АВС
касаются этой окружности. Значит,
окружность является вписанной
АВС.
В
M
K
О
С
L

9.

В любой треугольник можно
вписать окружность.
Теорема
А
M
K
О
С
L
В