Similar presentations:
Визначений інтеграл
1.
Тема. Визначений інтеграл2.
1.Означення визначеного інтеграла.2.Властивості визначеного інтеграла.
3.Теорема Ньютона-Лейбніца.
4.Метод заміни змінної та інтегрування
частинами у визначеному інтегралі.
5.Інтегрування парних та непарних
функцій у симетричних межах.
6.Геометричні застосування визначених
інтегралів.
7.Економічні застосування визначених
інтегралів.
3.
y f (x) - визначена і неперервна на a; bα1
x0=a
…
α2
x1
x2
…
αn
xn-1
xn=b
x
xi xi xi 1- довжина і-го частинного відрізка
S n f ( 1 ) x1 f ( 2 ) x2 ... f ( n ) xn
n
f ( i ) xi
i 1
- n-на інтегральна сума
4.
Визначеним інтегралом від функції f (x)на відрізку a; b називається границя
lim
max xk 0
n
S n S.
b
a
.
f ( x)dx
5.
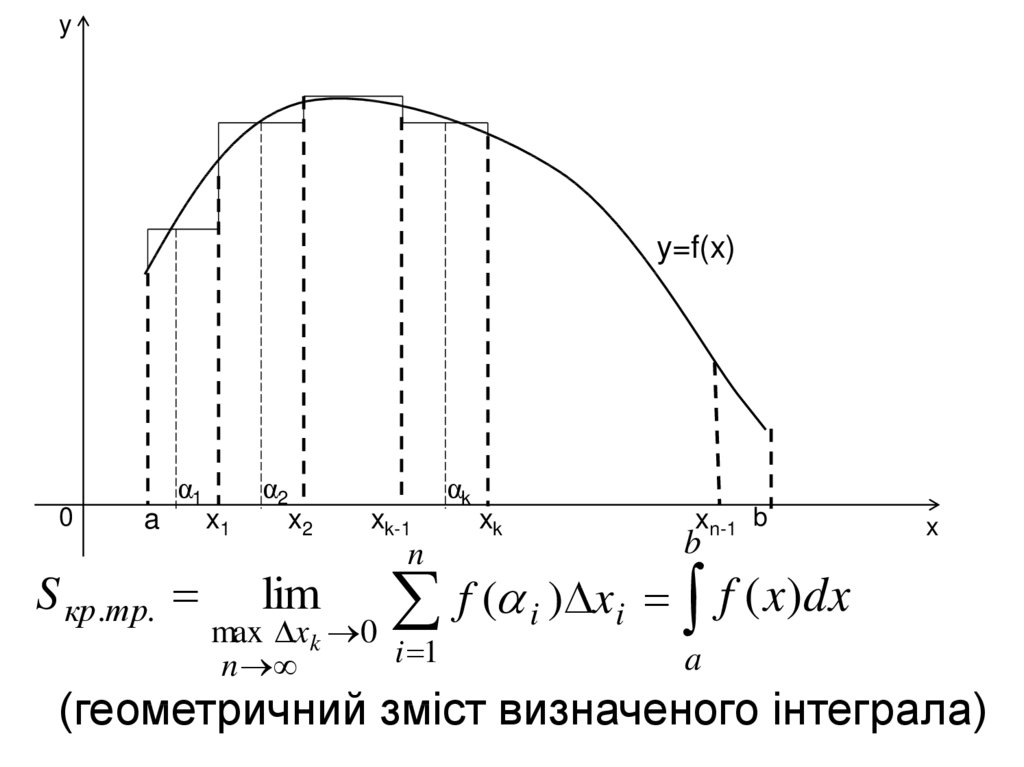
yy=f(x)
0
a
α1
S кр .тр.
x1
α2
x2
xk-1
αk
xk
xn-1 b
n
b
i 1
a
x
f ( i ) x i f ( x)dx
max x 0
lim
n
k
(геометричний зміст визначеного інтеграла)
6.
Основні властивості визначеного інтегралаb
b
b
a
a
a
1) f x dx f t dt f u du
a
2) f ( x)dx 0
a
b
a
a
b
3) f ( x)dx f ( x)dx
b
4) ( f1 ( x)
a
b
b
a
a
f 2 ( x)) dx f1 ( x)dx f 2 ( x)dx
7.
bb
a
a
5) k f ( x)dx k f ( x)dx
b
c
b
a
a
c
6) f ( x)dx f ( x)dx f ( x)dx
b
7) f ( x)dx f (c)(b a), (a c b)
a
8. Формула Ньютона - Лейбніца
bb
f ( x)dx = F (x)│a = F (b) - F (a)
a
.
9. Метод заміни змінної у визначеному інтегралі
ba
x (t )
dx (t )dt
f ( x)dx
f (t ) (t )dt
x a : a ( )
x b : b ( )
4
Приклад:
dx
1
0
x
10.
Метод інтегрування частинамиу визначеному інтегралі
b
u( x) dv( x) u( x) v( x)
a
e
Приклад:
ln
xdx
1
b
a
b
v( x) du ( x).
a
11.
2 f ( x)dx, якщо f ( x) парна,f
(
x
)
dx
0
a
0, якщо f ( x) непарна
a
a
1
Приклади:
xdx
1 x 2
1
4
e
4
x2
sin xdx





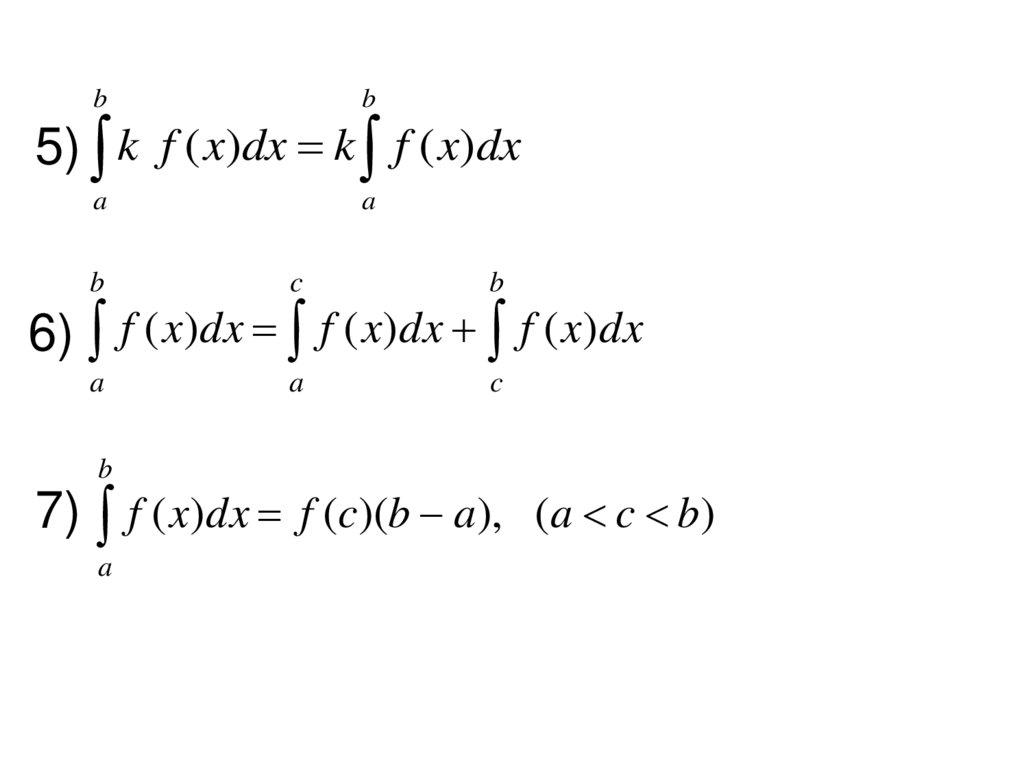



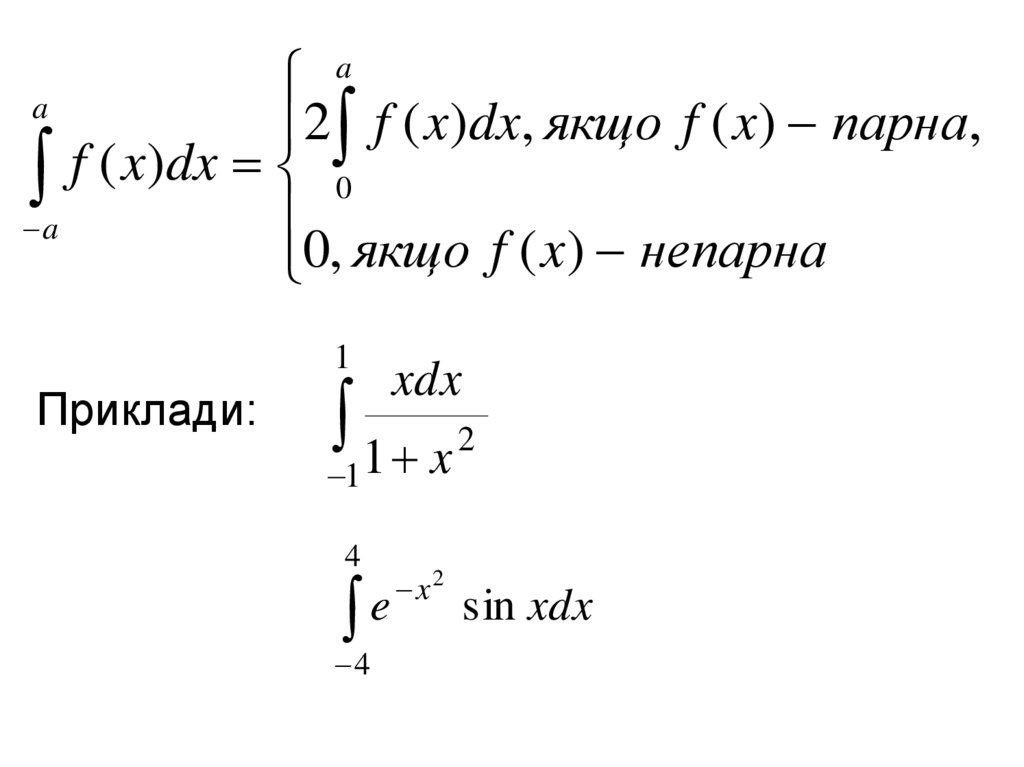
 mathematics
mathematics








