Визначений інтеграл і його застосування

1. Визначений інтеграл і його застосування

1. Визначений інтеграл і його властивості
2.Формула Ньютона-Лейбніца
3. Невласні інтеграли
4. Застосування інтегралів
5. Наближене обчислення визначених інтегралів

2. Визначений інтеграл і його застосування

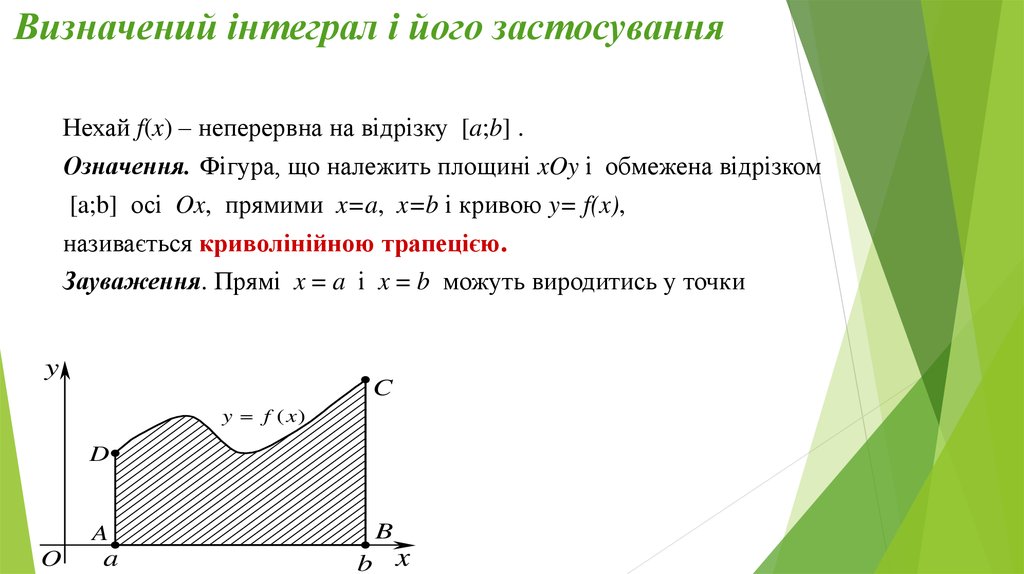
Нехай f(x) – неперервна на відрізку [a;b] .
Означення. Фігура, що належить площині xOy і обмежена відрізком
[a;b] осі Ox, прямими x=a, x=b і кривою y= f(x),
називається криволінійною трапецією.
Зауваження. Прямі x = a і x = b можуть виродитись у точки
y
C
y f ( x)
D
O
A
B
a
b x

3. Визначений інтеграл і його застосування

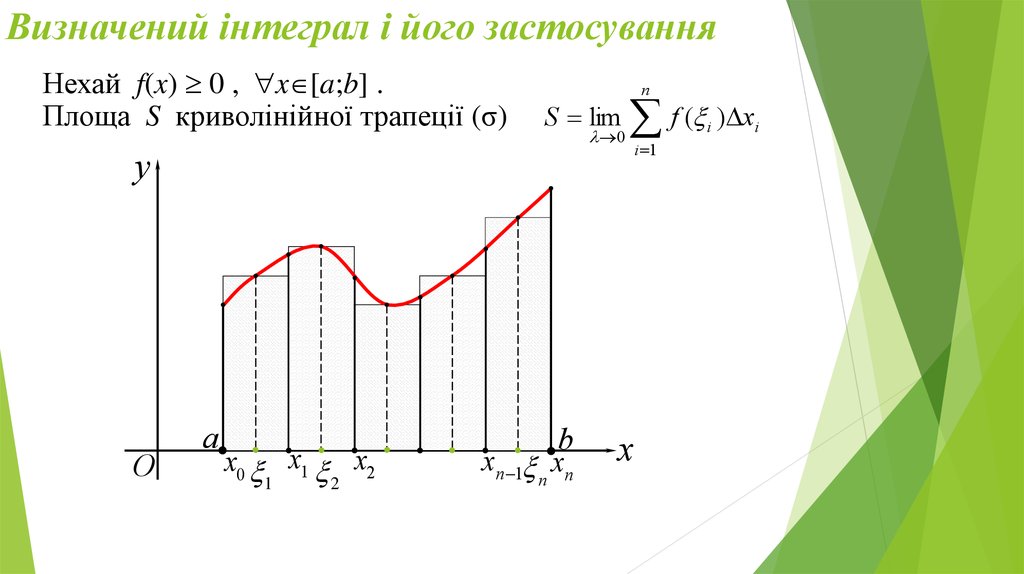
Нехай f(x) 0 , x [a;b] .
Площа S криволінійної трапеції (σ)
S lim
y
O
a
x0 x1 x2
2
1
b
xn 1 n xn
0
n
f ( ) x
x
i
i 1
i

4. Визначений інтеграл і його застосування

n
I n ( xi , i ) f ( i ) xi
i 1
max [ xi 1; xi ]
1 i n
- інтегральна сума для функції f(x) на відрізку [a;b].
Якщо існує границя сум In(xi, i) при 0, то її називають
визначеним інтегралом від функції f(x) на відрізку
[a;b] (або в межах від a до b).
b
ПОЗНАЧАЮТЬ:
f ( x )dx
a
a и b – нижня і верхня границя інтегрування,
[a;b] – проміжок інтегрування,
f(x) – підінтегральна функція,
f(x)dx – підінтегральний вираз,
x – змінна інтегрування.

5. Визначений інтеграл і його застосування

Функція f(x), для якої на [a;b] існує визначений інтеграл, називається
інтегрованою на цьому відрізку.
ТЕОРЕМА 1 (необхідна умова інтегрованості функції на [a;b]).
Якщо функція f(x) інтегрована на відрізку [a;b], то вона на
відрізку обмежена.
цьому
ТЕОРЕМА 2 (достатня умова інтегрованості функції на [a;b]).
Для інтегрованості функції f(x) на [a;b], достатньо виконання однієї з
умов:
1) f(x) неперервна на [a;b];
2) f(x) обмежена на [a;b] і має на [a;b] скінчене число точок розриву;
3) f(x) монотонна і обмежена на [a;b].

6. Визначений інтеграл і його застосування

Зауваження.
1) якщо a > b , то
b
a
a
b
f ( x)dx f ( x)dx ;
2) якщо a = b , то
a
f ( x)dx 0 .
a

7. Визначений інтеграл і його застосування

1) Геометричний зміст визначеного інтеграла.
Якщо функція f(x) – неперервна на [a;b] і f(x) 0 , x [a;b] , то
b
f ( x)dx S ,
a
де S – площа криволінійної трапеції с основою [a;b] і обмеженою
зверху кривою y = f(x).
2) Фізичний зміст визначеного інтеграла.
Якщо функція v = f(t) задає швидкість точки, що рухається в
T2
момент часу t , то
v(t )dt
T1
визначить шлях S, пройдений точкою за проміжок часу[T1 ; T2] .

8. Властивості визначеного інтеграла

b
1) dx b a .
a
b
b
a
a
2) kf ( x)dx k f ( x)dx
b
b
b
a
a
a
3) f ( x) ( x) dx f ( x)dx ( x)dx
b
c
b
a
a
c
4) f ( x)dx f ( x)dx f ( x)dx

9. Властивості визначеного інтеграла

5) Якщо f(x) > 0 (f(x) 0) x [a;b] , то
b
f ( x )dx 0
a
b
f ( x)dx 0
a
6) Якщо
f(x) (x) x [a;b] , то
b
b
a
a
f ( x)dx ( x)dx
7) Якщо m і M –відповідно найменше і найбільше
функції f(x) на відрізку [a;b], то
b
m(b a) f ( x)dx M (b a) .
a
a
8) Якщо f(x) – непарна функція, то
a
Якщо f(x) – парна функція, то
f ( x)dx 0.
a
a
f ( x)dx 2 f ( x)dx.
a
0
значення

10. Теорема про середнє

Якщо функція f(x) неперервна на [a;b], то в
інтервалі (a;b) знайдеться така точка
c, що
справедлива рівність
b
a
f ( x )dx (b a ) f (c)

11. Формула Ньютона-Лейбница

b
a
b
f ( x)dx F ( x) a F (b) F (a) .

12. Формула Ньютона-Лейбница

Заміна змінної
Інтегрування за частинами

13. Формула Ньютона-Лейбница

14. Формула Ньютона-Лейбница

15. Формула Ньютона-Лейбница

16. Невласні інтеграли

b
Для існування
f ( x)dx необхідне виконання умови:
a
1) [a;b] – скінченний,
2) f(x) – обмежена (необхідна умова існування визначеного
інтеграла).
Невласні інтеграли – узагальнене поняття визначеного
інтеграла у випадку коли одна з цих умов не виконується.

17. Невласні інтеграли I роду (за нескінченним проміжком)

ОЗНАЧЕННЯ. Невласним інтегралом I роду від функції
f(x) на проміжку [a;+ ) називається границя функції
I(b) при b + .
b
a
a
lim I (b) lim f ( x)dx
f ( x)dx b
b
Якщо y = f(x) неперервна на (– ;b] , то аналогічно
визначається і позначається Невласним інтегралом I
роду для функції f(x) на проміжку (– ;b]:
b
b
a
f ( x)dx .
f ( x)dx alim

18. Невласні інтеграли I роду

При цьому, якщо границя в правій частині формули існує і
скінченний, то невласний інтеграл називають збіжним.
У противному випадку ( якщо границя не існує або дорівнює
нескінченності) невласний інтеграл називають розбіжним.
Якщо y = f(x) неперервна на ℝ , то невласним інтегралом I роду для функції
f(x) на проміжку (– ;+ ) називають
c
f ( x)dx f ( x)dx f ( x)dx ,
(2)
c
де c – довільне число.
Невластный інтеграл від f(x) на промежутку (– ;+ ) називається збіжним,
якщо ОБИДВА інтеграла в правій частині формули (2) збігаються.
У протилежному випадку, невласний інтеграл на проміжку (– ;+ )
називається розбіжним.

19. Невласні інтеграли I роду

20. Невласні інтеграли I роду

21. Ознаки збіжності невласних інтегралів I роду

ТЕОРЕМА 1 (перша ознака збіжності).
Нехай f(x) і (x) неперервні на [a;+ ) і 0 f(x) (x) ,
x [c; + ) (де c a).
Тоді:
1) якщо
a
a
( x)dx – збіжний, то f ( x)dx теж збіжний ,
c
c
f ( x)dx ( x)dx ;
до того ж
2) якщо
( x)dx
a
– розбіжний, то
f ( x)dx теж розбіжний.
a

22. Ознаки збіжності невласних інтегралів I роду

ТЕОРЕМА 2 (друга ознака збіжності)
Нехай f(x) і (x) неперервні і невід'ємні на [a;+ ).
Якщо
f ( x)
lim
h , де h – дійсне число, відмінне від нуля,
x ( x)
то інтеграли
f ( x)dx
a
і
( x)dx
a
поводять себе однаково відносно збіжності.

23. Ознаки збіжності невласних інтегралів I роду

При використанні теорем 1 и 2 в якості «еталонних»
інтегралів зазвичай використовують наступні невласні
інтеграли:
збігається , при n 1,
dx
x n dx
a
розбігаєть ся при n 1.
(a 0)
e
0
x
dx
збігається , при 0 ,
розбігається, при 0 .

24. Ознаки збіжності невласних інтегралів I роду

ТЕОРЕМА 3 (ознака абсолютної збіжності).
Якщо збігається інтеграл
a
a
f ( x) dx , то і інтеграл f ( x)dx
теж буде збіжним сходиться.
При цьому інтеграл
збіжним.
a
f ( x )dx
називається абсолютно

25. Ознаки збіжності невласних інтегралів I роду

Якщо
f ( x) dx
розбіжний, то про інтеграл
a
f ( x)dx нічого
a
сказати неможна. Він може розбігатися, а може і збігатися.
Якщо
a
a
a
f ( x) dx розбіжний, а f ( x)dx – збіжний, то інтеграл
f ( x )dx
називається умовно збіжним

26. Невласні інтеграли IІ роду (від необмежених функцій)

ОЗНАЧЕННЯ. Невласним інтегралом IІ роду на проміжку
[a;b] від функції f(x), обмеженої в точці b називається
границя функції I(b1) при b1 b – 0 .
b1
b
I (b1 ) lim f ( x)dx
f ( x)dx b lim
b 0
b b 0
1
a
1
a
Якщо y=f(x) неперервна на (а;b] і x lima 0 f ( x) ( ) , то
аналогічно визначається і позначається невласний
інтеграл IІ роду для функції f(x) на проміжку [a;b]
від функції f(x), необмеженої в точці a
b
:
b
f ( x)dx a lima 0 f ( x)dx.
a
1
a1

27. Невласні інтеграли IІ роду

Якщо y = f(x) неперервна на [a;b]\{c} і x = c – точка
нескінченного розриву функції, то невласний інтеграл IІ
роду для функції f(x) на проміжку [a;b] називають
b
c
b
a
a
c
f ( x)dx f ( x)dx f ( x)dx.
Невласний інтеграл на проміжку [a;b] від функції f(x),
необмеженою всередині цього відрізку, називається
збіжним, якщо ОБИДВА інтеграла в правій частині
формули (2) збігаються.
У протилежному випадку, невласний інтеграл на проміжку
[a;b] називається розбіжним.

28. Невласні інтеграли IІ роду

29. Невласні інтеграли IІ роду

«Еталонні» інтеграли для невласних інтегралів IІ роду (від
необмежених функцій)
b
dx
(b x)n dx
a
b
dx
( x a)n dx
a
збігається , при n 1,
розбігається при n 1.
збігається , при n 1,
розбігається при n 1.

30. Довжина дуги кривої

Плоска крива, задана параметрично рівняннями
Нехай крива (ℓ) не має самоперетинів і задана
параметричним рівнянням: x (t ) ,
y (t ) ( t ) ,
де (t) , (t) – непрерывно диференційована на [ ; ] .
Довжина кривой (ℓ) .
( x (t )) 2 ( y (t )) 2 dt

31. Довжина дуги кривої

Плоска крива в полярних координатах
Нехай r = r( )
[ ; ] .
Довжина кривої
– неперервно диференційована на
r 2 (r ) 2 d .
r = r( ) , де [ ; ].
x = r cos , y = r sin

32. Обчислення об'єму тіла

За площею паралельних перерізів
Нехай (V) – замкнена і обмежена область у Oxyz (тіло).
Нехай S(x) (a x b) – площа довільного перерізу тіла
площиною, перпендикулярною до осі Ox.
Тоді об'єм тіла (V)
b
V S ( x)dx.
a

33. Об'єм тіла обертання

Нехай (V) – тіло, отримане в результаті обертання
навколо осі Ox криволінійної трапеції з основою
[a;b], обмеженою y = f(x) .
Об'єм цього тіла (V)
y
B
A
y f ( x)
b
Vx [ f ( x)]2 dx.
x
a
b
a

34. Об'єм тіла обертання

Нехай (V) – тіло, отримане в результаті обертання
навколо осі Ox області (σ), обмеженої лініями
x = a, x = b, y = f1(x), y = f2(x),
де 0 f1(x) f2(x), x [a;b].
Об'єм цього тіла (V)
y y f 2 ( x)
B
A y f1 ( x)
a
C
b
D
x
b
Vx [ f 2 ( x)]2 [ f1 ( x)]2 dx.
a

35. Наближене обчислення визначених інтегралів

Нехай y = f(x) – неперервна на [a;b]
елементарною.
b
Необхідно знайти
і її первісна не є
f ( x)dx.
a
5.1. Формула прямокутників
Розіб'ємо [a;b] на n рівних відрізків довжини h точками
x0 = a , x1 , x2 , … , xn = b (де x0 < x1 < x2 < … < xn ).
Нехай yi = f(xi) (i = 0,1,2,…,n). Складемо суми
Sn = y0h + y1h + y2h + … + yn–1h ,
S̃n = y1h + y2h + y3h + … + ynh ,
b a
h
де
– довжина відрізків [xi–1 ; xi] (i = 1,2,…,n).
n

36. Наближене обчислення визначених інтегралів

Sn і S̃n – інтегральні суми для f(x) на відрізку [a;b].
b
b
(1)
f
(
x
)
dx
S
h
y
y
y
y
,
n
0
1
2
n
1
a
~
f ( x)dx Sn h y1 y2 y3 yn .
(2)
a
Нехай Rn – модуль різниці між точними значеннями визначеного
інтеграла і його наближеним значенням.
M1
Rn
(b a) 2 ,
2n
де M1 max f ( x) .
Тоді
[ a ,b ]
Формули (1) и (2) називаються формулами прямокутників

37. Наближене обчислення визначених інтегралів

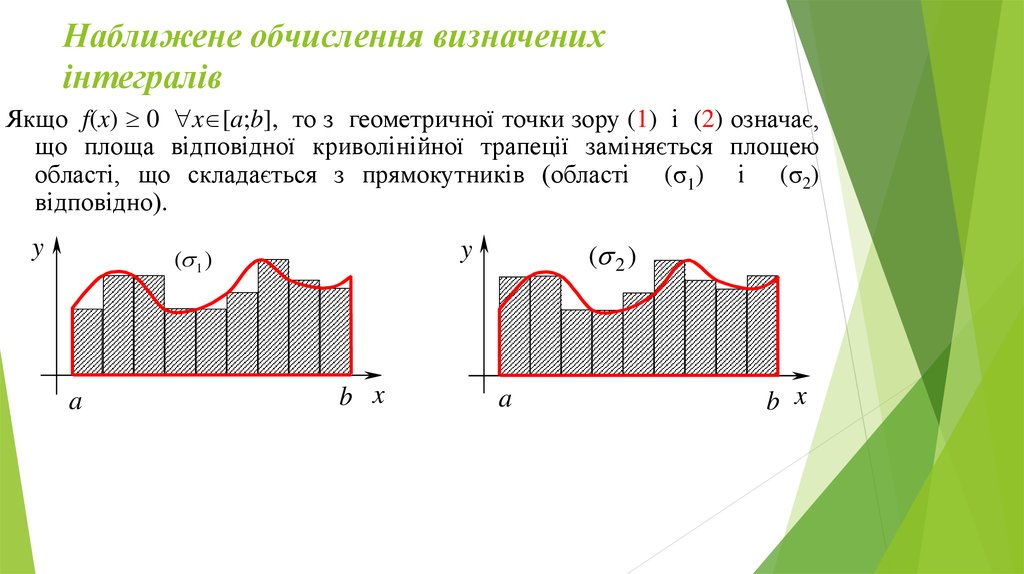
Якщо f(x) 0 x [a;b], то з геометричної точки зору (1) і (2) означає,
що площа відповідної криволінійної трапеції заміняється площею
області, що складається з прямокутників (області (σ1) і (σ2)
відповідно).
y
( 2 )
y
( 1 )
( 2 )
a
b x
a
b x

38. Наближене обчислення визначених інтегралів

Формула трапеції
Розіб'ємо [a;b] на n рівних відрізків довжини h точками
x0 = a , x1 , x2 , … , xn = b (де x0 < x1 < x2 < … < xn ).
Нехай yi = f(xi) (i = 0,1,2,…,n).
Тоді
b
h
f ( x)dx 2 y0 yn 2( y1 y2 yn 1) ,
a
b a
де
– довжина відрізків [xi–1 ; xi] (i = 1,2,…,n).
n
M2
3
Для формули (3)
Rn
(
b
a
)
,
2
12 n
де M max f ( x) .
2
h
[ a ,b ]
(3)

39.

Формула (3) називається формулою трапеції.
Якщо f(x) 0 x [a;b], то з геометричної точки зору (3)
означає, що площа відповідної криволінійної трапеції
заміняється
y площею області, що складається з трапецій.
a
b
x