Similar presentations:
Алгоритм построения сечений многогранников. Сечения призмы
1.
«Величие человека - в егоспособности мыслить»
(Б. Паскаль)
2.
«Величие человека - в его способности мыслить.»(Б. Паскаль)
3.
4.
Алгоритм построения сечениймногогранников:
1) проводим прямые через точки, лежащие в
одной плоскости;
2) ищем прямые пересечения плоскости сечения
с гранями многогранника, для этого:
а) ищем точки пересечения прямой
принадлежащей плоскости сечения с прямой,
принадлежащей одной из граней (лежащие в
одной плоскости);
б) параллельные грани плоскость сечения
пересекает по параллельным прямым.
5. ВАЖНО!
Для построения сечений ищем отрезки,по которым секущая плоскость пересекает
каждую грань.
Можно соединять только точки, которые
лежат в одной плоскости.
Если
секущая плоскость пересекает
противоположные грани, то она пересекает
их по параллельным отрезкам.
6.
1. Построить сечение многогранника,проходящее через выделенные элементы
7.
2. Построить сечение, проходящее через точкуО, параллельно грани ABCD
О
B
A
C
D
8.
4. Построить сечение многогранника ,проходящее через выделенные элементы
Провести дополнительное построению параллельно выполненному
сечению
9.
7. Построить сечение параллелепипеда, проходящеечерез заданные точки
Способ 1
B1
C1
Н
A1
D1
I
B
C
F
K
A
D
L
10.
Краткая запись решения1. H ↔ I
2. H ↔ F
3. FL || HI
4. FL ∩ AD = L
5. IK || HF
6. IK ∩ DC = K
7. L ↔ K
HIKLF – искомое сечение
11.
7. Построить сечение параллелепипеда, проходящеечерез заданные точки
Способ 2
B1
C1
Н
A1
D1
I
B
C
F
K
A
D
L
X
Y
12.
Краткая запись решения1. H ↔ F
2. H ↔ I
3. HF ∩ BA = X
4. HI ∩ BC =Y
5. XY ∩ AD = L
6. XY ∩ CD = K
7. F ↔ L
8. I ↔ K
HIKLF – искомое сечение
13.
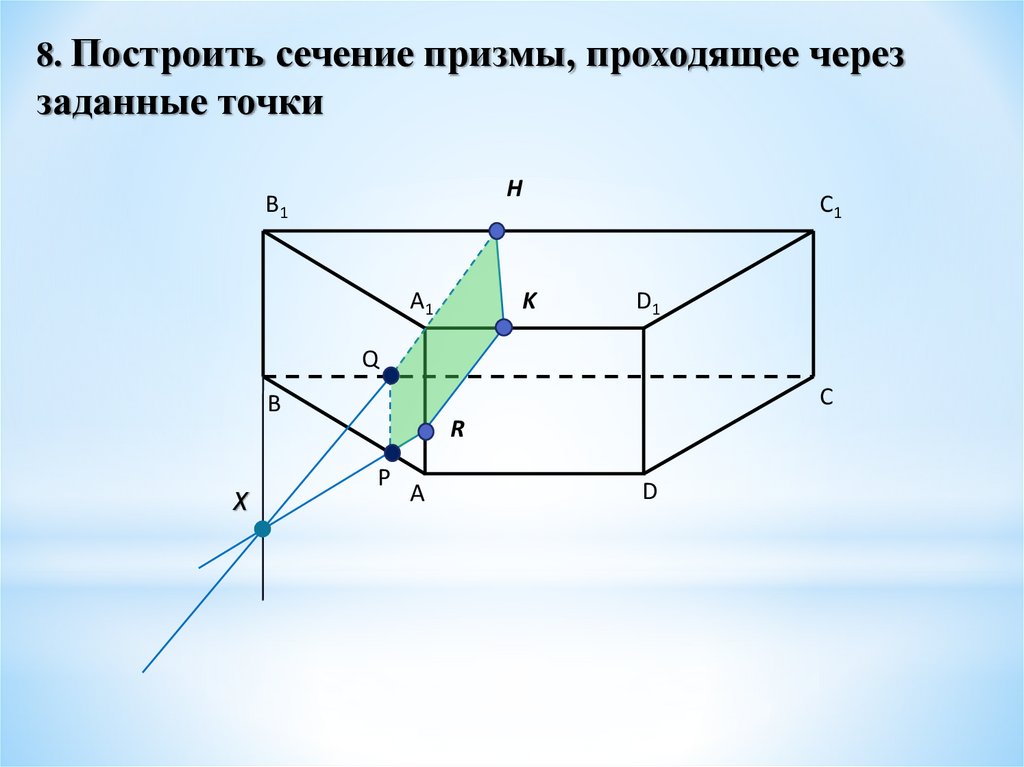
8. Построить сечение призмы, проходящее череззаданные точки
Н
B1
A1
K
C1
D1
Q
C
B
X
R
P
A
D
14.
Краткая запись решения1. H ↔ K
2. K ↔ R
3. HQ || KR
4. HQ ∩ B1B =X
5. X ↔ R
6. XR ∩ AB =P
7. P ↔ Q
HKRPQ – искомое
сечение














 mathematics
mathematics








