Similar presentations:
Тождественные преобразования тригонометрических выражений
1.
2. Тождественные преобразования тригонометрических выражений
3. Рекомендации.
Выполнение преобразований тригонометрическихвыражений рекомендуется начинать с анализа структуры
данного выражения и составления плана действий. Иногда
могут быть полезны следующие рекомендации:
1.Если выражение содержит разные
тригонометрические функции одного аргумента, то
попробуйте все функции выразить через одну или две
функции. При этом тангенс и котангенс угла чаще всего
выражают через синус и косинус этого же угла;
2.Если в выражение входят тригонометрические
функции от разных аргументов, то попытайтесь свести
все функции к одному аргументу;
3.Формулы приведения могут быть полезны для
выражения тригонометрической функции через
кофункцию;
4.
4. Не забывайте о формулах сокращенногоумножения - они могут иногда помочь в
преобразовании тригонометрического выражения;
5. Если в выражении нет нужного слагаемого, то
его можно прибавить и сразу же вычесть. Иногда
полезно какое - то слагаемое представить в виде
суммы двух или нескольких слагаемых. Наконец,
единицу бывает полезным представить в виде:
1 cos 2 sin 2
6. Если в выражении нет нужного множителя, то
на него можно умножить и сразу же разделить
данное выражение (при условии, что этот
множитель отличен от нуля);
5.
7. Попробуйте применить метод введениявспомогательного угла. В простейших случаях он
сводится к замене чисел 1 ; 2 ; 3 ; 3 ; 3;1
2
2
2
3
тригонометрическими функциями
соответствующих углов;
8. Если в выражение входят степени
тригонометрических функций, то можно обратиться к
преобразованиям, понижающим степени;
9. Если данное выражение является однородным
многочленом n-ой степени относительно cos и sin
то преобразование можно выполнять путем
вынесения за скобки cos n и sin n
6.
Тождественные преобразования тригонометрическихвыражений опираются на следующие основные
формулы:
Формулы приведения.
Формулы для тригонометрических функций одного и
того же аргумента.
Формулы сложения аргументов.
Формулы двойного угла.
Формулы половинного аргумента.
Формулы преобразования суммы(разности)
тригонометрических функций в произведение.
Формулы преобразования произведения
тригонометрических функций в сумму( разность).
7.
3sin( ) sin
3
3
2
ctg ( ) ctg 3
6
6
2
cos( 45 ) cos 45
2
0
0
tg ( 60 ) tg 60 3
0
0
2
sin 405 sin( 360 45 ) sin 45
2
0
0
0
0
2
sin( 765 ) sin 765 sin( 2 360 45 ) sin 45
2
0
0
0
0
0
8.
1716
tg
tg (
) tg (4 ) tg 1
4
4
4
4
4
13
12
ctg (
) ctg (
) ctg (2 ) ctg 3
6
6
6
6
6
25
25
24
3
cos(
) cos
cos(
) cos
6
6
6
6
6
2
9.
Если функция стоит в четной степени, томожно не обращать внимание на четверть и не
стоит определять знак функции, а только
посмотреть меняем ли на кофункцию.
cos (270 ) sin
2
0
2
В случае, если аргумент записан в виде ( - )
sin( ) sin( ( )) sin( ) sin
cos( 900 ) cos( (900 )) cos(900 ) sin
10.
cos( 2 ) cos (270 )0
tg ( ) sin( 90 )
2
0
cos( 2 ) cos( 2 ) cos
2
2
2
0
2
sin sin
cos (270 ) sin sin
tg ( ) tg ( ( )) tg ( ) tg
tg
1
cos
0
sin(
90
) cos
sin cos
sin
2
sin cos
11.
2sin 2 1 cos 2
sin
2. tg
cos
cos 1 sin
cos
ctg
sin
1. sin cos 1
2
2
3. tg ctg 1
1
4. 1 tg
cos 2
2
1
5. 1 ctg
2
sin
2
2
1
1
tg
; ctg
ctg
tg
12.
Пример 1.3
3
Вычислить tg , зная что sin ,
5
2
3 2
9
16
2
2
cos 1 sin 1 ( ) 1
;
5
25 25
4
4
cos
или cos ,
5
5
так как по условию III четверти,
а cos 0 в III четверти,
4
то берем cos ,
5
3
4
3
тогда tg ( )
5
5
4
13.
4sin
cos
Пример 2. Вычислить
, если tg =4 .
sin 3 cos
4 sin cos
cos cos 4tg - 1 4 4 1 16 1 15
sin 3 cos
tg
3
4
3
1
cos cos
Примечание: если будет известно значение ctg , то
необходимо разделить на sin .
14.
Пример 3. Найти cos2 , если tg =1/2.Используем формулу:
1 2
1
1 ( )
1
2
3 5 3
1 tg
2
4
cos 2
1 tg 2 1 ( 1 ) 2 1 1 4 4 5
2
4
15.
5Пример 4. Найти tg , если известно, что cos 2
13
и III четверти.
1 tg 2
5
cos 2
2
1 tg
13
5 1 tg 2 13 1 tg 2
5tg
13
tg13
13
13tg
5
5 tg
2
2
2
2
8tg 2 18
9
18
tg
48
3
tg
2
2
Так как tg в третьей четверти
принимает положительные
3
значения, то
tg
2
16.
Пример 5. Вычислить sin , если sin2
cos
2
2
sin cos 1,4
2
2
2
sin
2
(sin
2
2
2
2 sin
cos
2
2
2
cos
2
cos
) sin 2
1 sin 1,96 1
,96
sin 0 ,096
2
2
2
1,96
1,96
1,4 .
17.
sin( ) sin cos cos sincos( ) cos cos sin sin
cos( ) cos cos sin sin
tg tg
tg ( )
1 tg tg
tg tg
tg ( )
1 tg tg
Пример 1. Вычислить cos18 cos12 sin 18 sin 12
cos18 cos12 sin 18 sin 12 cos(18 12 )
3
cos 30
2
18.
33
cos cos
sin
Пример 2. Вычислить sin
4
12
4
12
3
3
3
sin
cos cos
sin
sin(
)
4
12
4
12
4 12
5
6
10
sin(
)
sin
sin
6
6 6
12
1
sin( ) sin
6
6 2
19.
cos 4 cos sin 4 sinПример 3. Упростить:
sin 3
cos( 4 )
cos 4 cos sin 4 sin
sin 3
sin 3
cos 3
ctg 3
sin 3
20.
Пример 4. Упростить:tgx tg ( x)
6
1 tgx tg ( x)
6
tgx tg ( x)
6
tg ( x ( x ))
6
1 tgx tg ( x)
6
3
tg ( x x) tg
6
6
3
21.
Пример 5. Упростить:sin( ) 2 cos sin
sin( )
sin( ) 2 cos sin
sin( )
sin cos cos sin 2 cos sin
sin( )
sin cos cos sin sin( )
1
sin( )
sin( )
22.
53
Пример 6. sin , cos ; , IV четверти
13
5
Найти: sin( + ).
Применим формулу sin( + )=sin cos +cos sin
5 2
25 144
12
cos 1 sin , cos 1 ( ) 1
; cos
13
169 169
13
12
ò .ê. IV÷åòâåðòè cos
13
2
2
2
3 2
9 16
4
sin 1 cos , sin 1 ( ) 1
; sin
5
25 25
5
4
ò .ê. IV÷åòâåðòè sin
5
5 3 12
4
3
48
15 48
63
sin( ) ( ) ( )
13 5 13
5
13
65
65
65
2
2
2
23.
Пример 7. Вычислить tg , если tg =1 , tg( - )=-2tg - tg
tg( - )
1 tg tg
tg - tg
2
1 tg tg
1 - tg
2
1 tg
1 - tg 2 (1 tg )
1 - tg 2 - 2 tg
- tg 2 tg 2 1
tg 3
24.
Формулы двойного углаsin 2 2 sin cos
Примеры:
Примеры:
sin 4 x 2 sin 2 x cos 2 x
sin 2 sin
cos 2 cos 2 sin 2
cos
2
2
2 sin 100 cos 100 sin 200
2tg
tg 2
1 tg 2
0
2
tg
60
tg1200
1 tg 2 600
cos 100 0 cos 2 500 sin 2 500
cos 8 cos 2 4 sin 2 4
cos 2 250 sin 2 250 cos 500
1 tg 2
сtg 2
2tg
25.
Формулы двойного углаУпростить:
sin 800
2 sin 400 cos 400
0
sin
40
2 cos 400
2 cos 400
(cos
8
sin
8
)(cos
sin 750 cos 750
8
sin
8
) cos
2
8
sin
2
8
cos 2
8
cos
4
2
1
1
1
1
sin 750 cos 750 sin 1500 sin( 1800 300 ) sin 300
2
2
2
2
4
sin cos 3 sin 3 cos sin cos (cos 2 sin 2 ) sin cos cos 2
2
1
1 2
1
sin cos cos 2 sin 2 cos 2 sin 2 cos 2 sin 4
2
2
2 2
4
26.
Формулы суммы и разности тригонометрическихфункций
sin sin 2 sin
cos
2
2
sin sin 2 sin
cos
2
2
cos cos 2 cos
cos
2
2
cos cos 2 sin
sin
2
2
sin( )
tg tg
cos cos
sin( )
tg tg
cos cos
27.
Формулы суммы и разности тригонометрическихфункций
Пример 1.
50 10
50 10
2 sin
sin
cos 50 cos 10
2
2
sin 20
sin 20
2 sin 20 sin 30
1
2 sin 30 2 1
sin 20
2.
28.
Формулы суммы и разности тригонометрическихфункций
Пример 2.
2 8
2 8
cos
cos 2 cos 8 2 cos
2
2
10
( 6 )
2 cos
cos
2 cos 5 cos( 3 )
2
2
2 cos 5 cos 3
29.
Формулы суммы и разности тригонометрическихфункций
Пример 3.
2
4
sin sin
2 sin 4 12 cos 4 12 2 sin 12 cos 12
4
12
2
2
2
2
2 3
6
3
2 sin cos 2 sin cos
cos 3 cos
12
12
6
2
12
2
2
30.
Формулы суммы и разности тригонометрическихфункций
Пример 4.
sin x sin 2x sin 3x sin 4x
(sin x sin 3x) (sin 2 x sin 4 x)
x 3x
x 3x
2x 4x
2x 4x
2 sin
cos
2 sin
cos
2
2
2
2
2 sin 2x cos x 2 sin 3x cos x 2 cos x (sin 2 x sin 3x)
5x
x
5x
x
cos
2 cos x 2 sin
cos( ) 4 cos x sin
2
2
2
2
31.
Вычислить:tg 200 tg 400 tg600 ........ tg1600 tg1800
(tg 200 tg1600 ) (tg 400 tg1400 ) (tg600 tg1200 ) (tg800 tg1000 ) tg1800
sin( 200 1600 )
sin( 400 1400 )
sin( 600 1200 )
sin( 800 1000 )
0
tg
180
0
0
0
0
0
0
0
0
0
cos 20 cos160 cos 40 cos140 cos 60 cos120 cos 80 cos100
32.
26
... cos
.
Вычислить: cos 0 cos cos
7
7
7
2
6
6
cos 0 cos cos
... cos
1 (cos cos )
7
7
7
7
7
(cos
2
5
3
4
cos ) (cos
cos )
7
7
7
7
Воспользуемся формулой: cos cos 2 cos
cos
2
2
cos
0
Получим:
5
3
1 2 cos cos
2 cos cos
2 cos cos 1
2
14
2
14
2
14
2
33.
Вычислить: sin 90 sin 490 ... sin 2890 sin 3290При выполнении задания можно воспользоваться формулой из
учебника М.Л.Галицкого «Сборник задач по алгебре 8 – 9 класс»
Пусть (аn) – арифметическая прогрессия с разностью d и
Sn=sin a1+sin a2+…+sin an.
Sn
sin
dn
d (n 1)
sin( a1
)
2
2
d
sin
2
В нашем случае a1=90, d=400, n=9, следовательно:
40 0 9
40 0 8
0
sin
sin( 9
)
0
0
sin
180
sin
169
2
2
S9
0
0
0
40
sin 20
sin
2
т.к. sin 180 0 0
34.
Sn=cos a1+cos a2+…+cos an.dn
d (n 1)
sin
cos( a1
)
2
2
Sn
d
sin
2
35.
sin 8 sin 9 sin 10 sin 11 sin 12cos 8 cos 9 cos10 cos11 cos12
Вычислите его значение, если tg5 18 .
sin 8 sin 9 sin 10 sin 11 sin 12
sin
cos 8 cos 9 cos10 cos11 cos12
sin
5
4
5
sin( 8
) sin
sin 10
2
2
2
sin
sin
2
2
5
4
5
cos(8
) sin
cos10
2
2
2
sin
sin
2
2
5
1
sin 10
2
1 64 16
2tg5
8
2
tg10
2
1
5
4 63 63
1
tg
5
1
sin
cos10
64
2
sin
36.
n(n 1)
sin
sin
2
2
sin sin 2 sin 3 ... sin n
sin
2
n
(n 1)
sin
cos
2
2
cos cos 2 cos 3 ... cos n
sin
2
37.
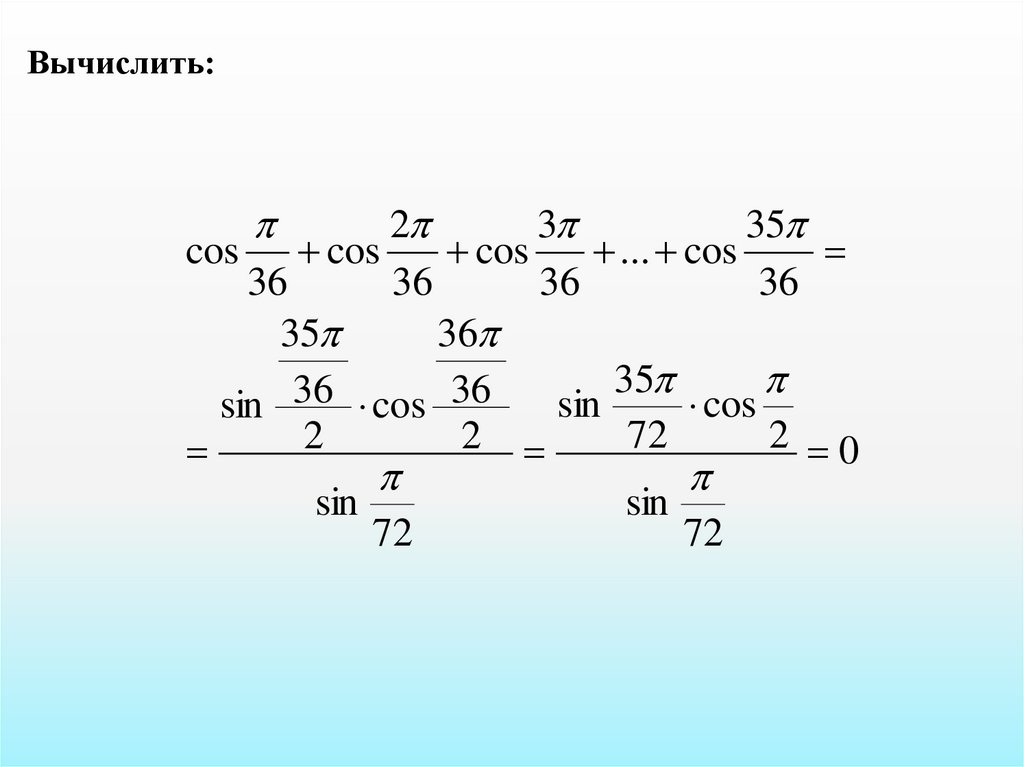
Вычислить:2
3
35
cos cos
cos
... cos
36
36
36
36
35
36
35
36
36
sin
cos
sin
cos
72
2 0
2
2
sin
72
sin
72
38.
sin sin 2 ... sin 17Вычислить:
cos cos 2 ... cos 17
17
18
17
sin
sin
sin
sin 9
2
2
2
sin sin 2 ... sin 17
sin
sin
2
2
cos cos 2 ... cos17
sin
17
18
17
cos
sin
cos 9
2
2
2
sin
sin
2
2
17
sin 9
sin sin 2 ... sin 17
2
tg9
cos cos 2 ... cos17 sin 17 cos 9
2
sin
39. Вычислите значение выражения
cos 11 3 cos 9 3 cos 7 cos 5cos 8
если
1
cos
3
cos 11 3(cos 9 cos 7 ) cos 5
cos 8
2 cos 8 cos 3 6 cos 8 cos
cos 8
2 cos 8 (cos 3 3 cos )
cos 8
2(4 cos 3 3 cos 3 cos )
1
8
8 cos 8
27 27
3
40.
Формулы понижения степени1 cos 2
cos
2
2
1 cos 2
sin
2
3 cos cos 3
cos 3
4
3 sin sin 3
3
sin
4
2
41.
I способВычислить: 125 (cos8 sin 8 ), åñëè cos 2 0,8.
125 (cos 8 sin 8 ) 125 (cos 4 sin 4 )(cos 4 sin 4 )
125 (cos 2 sin 2 ) (cos 2 sin 2 ) (cos 4 sin 4 )
125 cos 2 (cos 4 sin 4 ) 125 0,8 (cos 4 sin 4 )
1 cos 2 2 1 cos 2 2
1 0.8 2 1 0.8 2
100 [(
) (
) ] 100 [(
) (
) ]
2
2
2
2
100 (0,92 0,12 ) 100 (0,81 0,01) 100 0,82 82
42.
II способВычислить 125 (cos8 sin 8 ) , åñëè cos 2 0,8
:
125 (cos 8 sin 8 ) 125 (cos 4 sin 4 ) (cos 4 sin 4 )
125 (cos 2 sin 2 ) (cos 2 sin 2 ) (cos 4 sin 4 )
125 cos 2 (cos 4 sin 4 ) 125 0,8 (cos 4 sin 4 )
100 (cos 4 sin 4 )
100 [(cos 4 2 sin 2 cos 2 sin 4 ) 2 sin 2 cos 2 ]
100 [(cos 2 sin 2 ) 2 2 sin 2 cos 2 ]
4 sin 2 cos 2
sin 2 2
100 (1
) 100 (1
)
2
2
1 cos 2 2
2 1 0,64
100 (1
) 100 (
) 100 0,82 82
2
2
43.
1sin sin [cos( ) cos( )]
2
1
cos cos [cos( ) cos( )]
2
1
sin cos [sin( ) sin( )]
2
44.
Пример: sin x sin 3x sin 4x sin 8x1
1
[cos( x 3x) cos( x 3x)] [cos( 4 x 8 x) cos( 4 x 8 x)]
2
2
1
1
[cos( 2 x) cos 4 x] [cos( 4 x) cos12 x]
2
2
1
1
(cos 2 x cos 4 x cos 4 x cos 12 x) (cos 2 x cos12 x)
2
2
1
2 x 12 x
2 x 12 x
( 2 sin
sin
) sin( 5 x) sin 7 x
2
2
2
sin 5x sin 7 x
45.
Доказать тождество:sin( ) sin( ) sin 2 sin 2
sin( ) sin( ) (sin cos sin cos )
(sin cos sin cos ) sin 2 cos 2 sin 2 cos 2
sin 2 (1 sin 2 ) sin 2 (1 sin 2 )
sin 2 sin 2 sin 2 sin 2 sin 2 sin 2 sin 2 sin 2
46. 1 способ
2sin (
sin(
2
2 ) sin (
2
2
2
2
sin sin 4
2
2 )
2 ) sin(
2
2
2
2 )
Применили формулу
sin( ) sin( ) sin sin
2
2
47. 2 способ
sin 2 (2
2 ) sin 2 (
2
2 )
)
2
sin(
)
2
sin(
)
2
sin(
)
2
sin(
2
2
2
2
2 sin 2
2 sin 2
2
2
2
2
2
2
2
2
2 sin 2 cos
2
2 sin
cos 2
cos 2
2
2
2
2
2
2
2
2
2
cos 2 sin 4 sin
48.
3 способ2
sin (
2
2 ) sin (
2
2
2 )
2 ) 1 cos 2( 2 )
2
2
2
2
1 cos( 4 ) 1 cos( 4 ) cos( 4 ) cos( 4 )
2
2
4 4
4 4
2 sin
sin
2
2
2
sin sin( 4 ) sin sin 4
1 cos 2(
49.
sin ( ) sin ( )8 2
8 2
2
sin(
8
2
2
8
) sin(
2
8
2
sin sin
sin
4
2
2
8
2
)
50.
Упроститеcos 2 2 sin( 30 ) sin( 30 )
cos 2 sin 2 2(sin 2 sin 2 30 )
1
cos sin 2 sin
2
1
1 1
2
2
cos sin 1
2
2 2
2
2
2
51.
1Доказать тождество: sin sin( 60 ) sin( 60 ) sin 3
4
0
0
sin sin( 600 ) sin( 600 ) sin (sin 2 600 sin 2 )
1
3
1
2
3
sin ( sin ) (3 sin 4 sin ) sin 3
4
4
4
52.
Аналогично доказываются тождества:1
cos cos(60 ) cos(60 ) cos 3
4
tg tg(600 ) tg(600 ) tg3
0
0
ctg ctg(600 ) ctg(600 ) ctg3
Пользуясь этими тождествами легко доказать, что:
1
3
0
sin 20 sin 40 sin 80 sin 60
4
8
0
0
0
1
3
0
cos10 cos 50 cos 70 cos 30
4
8
0
0
0
tg60 tg540 tg660 tg180
53.
Вычислить:tg 200 tg 400 tg600 tg800 (tg 200 tg 400 tg800 ) tg600 tg600 tg600
3 3 3
Второй способ:
0
0
0
sin
20
sin
40
sin
80
tg 200 tg 400 tg600 tg800
3
0
0
0
cos 20 cos 40 cos 80
1
8 3 cos100 sin 200 sin 400 8 3 cos100 (cos 200 cos 600 )
2
1
1
0
0
0
0
0
8 3 cos10 ( cos 20 ) 4 3 cos10 cos 20 2 3 cos10
2
4
3 1
1
0
0
0
cos100 ) 2 3 cos100
4 3 ( (cos 30 cos10 )) 2 3 cos10 4 3 (
4 2
2
3 2 3 cos100 2 3 cos100 3
54.
Вычислить: cos120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 8401
cos 24 cos 36 cos 84 cos 720
4
1
0
0
0
cos12 cos 48 cos 72 cos 360
4
0
0
0
cos120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 840
1
1
0 1
0
0
0
0 1
cos 72 cos 36 cos 60 cos 72 cos 36
4
4
16
2
cos 720 cos 360 cos 720 2 cos 360 sin 360 cos 720 sin 720
0
0
32
2 32 sin 36
64 sin 36
1
sin 1440
sin 360
sin( 1800 360 )
0
0
0
128
128 sin 36
128 sin 36
128 sin 36
55.
Вычислить: cos120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 840cos 120 cos 240 cos 360 cos 480 cos 600 cos 720 cos 840
0
0
2 sin 120 cos120
2
sin
36
cos
36
1
0
0
0
0
0
cos 24
cos 48 cos 72 cos(90 6 )
0
0
2 sin 12
2 sin 36
2
2 sin 240 cos 240 2 sin 720 cos 720 cos 480 sin 60
0
0
4 8 sin 12 sin 36
2 sin 480 cos 480 sin 1440 sin 60 sin 960 sin 360 sin 60
0
0
0
2 32 sin 12 sin 36
64 sin 12 sin 36
sin 120
1
2 cos 60 sin 60
0
0
128 sin 12 128
2 64 sin 12
56.
Примеры преобразований тригонометрических выраженийчасто встречающиеся или имеющие необычный подход в решении
Пример1:
2sin20 0 cos20 0 cos40 0 cos80 0 2 sin 800 cos 800
0
0
0
cos20 сos40 cos80
2sin20 0
2 4 sin 200
sin 1600 sin( 1800 200 ) sin 200 1
0
0
0
8 sin 20
8 sin 20
8 sin 20
8
Способ 2
1
1 1 1
cos20 0 сos40 0 cos80 0 cos 60
4
4 2 8
Применили формулу
cos cos(60 ) cos(60 )
1
cos 3
4
57.
Пример 2:tg10 tg30 tg50...tg890
tg890 tg(900 10 ) сtg10
tg870 tg(900 30 ) сtg30
tg850 tg(900 50 ) сtg50
и т.д., кроме этого:
tg 470 tg(900 430 ) сtg 430
умножим:
tg10 tg890 tg10 сtg10 1
все попарные произведения дают 1, а tg450=1. следовательно все
выражение равно 1.
58.
Вычислить:1 cos 6 1 cos 2 1
cos 3 cos 1 cos 4 cos 2
(cos 6 cos 2)
2
2
2
2
2
1 1
1 1
1
1
cos 6 cos 2 cos 6 cos 2 1
2 2
2 2
2
2
59. Преобразовать в произведение.
35
2 cos ( ) 3 cos( ) 1
2 2
2
2
2 sin
2
2 sin
2
sin
2
2
2
2
3 sin 1
3 sin cos
cos
2
2
2
2
sin
2
2
3 sin
3
1
cos 3 sin 2( sin cos )
2
2
2(sin cos 30 cos sin 30 ) 2 sin( 30 )
60.
34
Вычислить: sin( arctg arcctg ).
4
3
Воспользуемся формулами перехода от одной обратной
тригонометрической функции к другой:
x
1
1
arctg x arcsin
arccos
arcctg
x
1 x2
1 x2
åñëè 0 x ,
3
3
4
тогда arctg arcсtg , получим sin (2arсtg )
4
4
3
3
34
3 5
3
arсtg arcsin
arcsin arcsin
4
4 4
5
1 9 16
3
3
3
4
sin(2 arcsin ), ïóñòü arcsin , òîãäà sin , cos , I ÷åòâ.
5
5
5
5
3
3 4 24
sin(2 arcsin ) sin 2 2 sin cos 2
5
5 5 25
61. Используемая литература
А. Н. Шыныбеков «Алгебра и начала анализа». Алматы«Атамура» 2006 г.
М. Л. Галицкий «Сборник задач по алгебре 8-9». Москва
«Просвещение» 2005 г.
Яремчук Ф.П, Рудченко П.А. «Алгебра и элементарные
функции». Киев «Наукова думка» 1987 г.
Цыпкин А. Г, Пинский А.И. «Справочное пособие по
методам решения задач по математике для средней
школы». Москва «Наука» 1983 г.
И.П. Рустюмова, С.Т. Рустюмова «Пособие для
подготовки к ЕНТ по математике». Алматы 2010 г.
Сборники тестов по математике 2003-2011 гг.









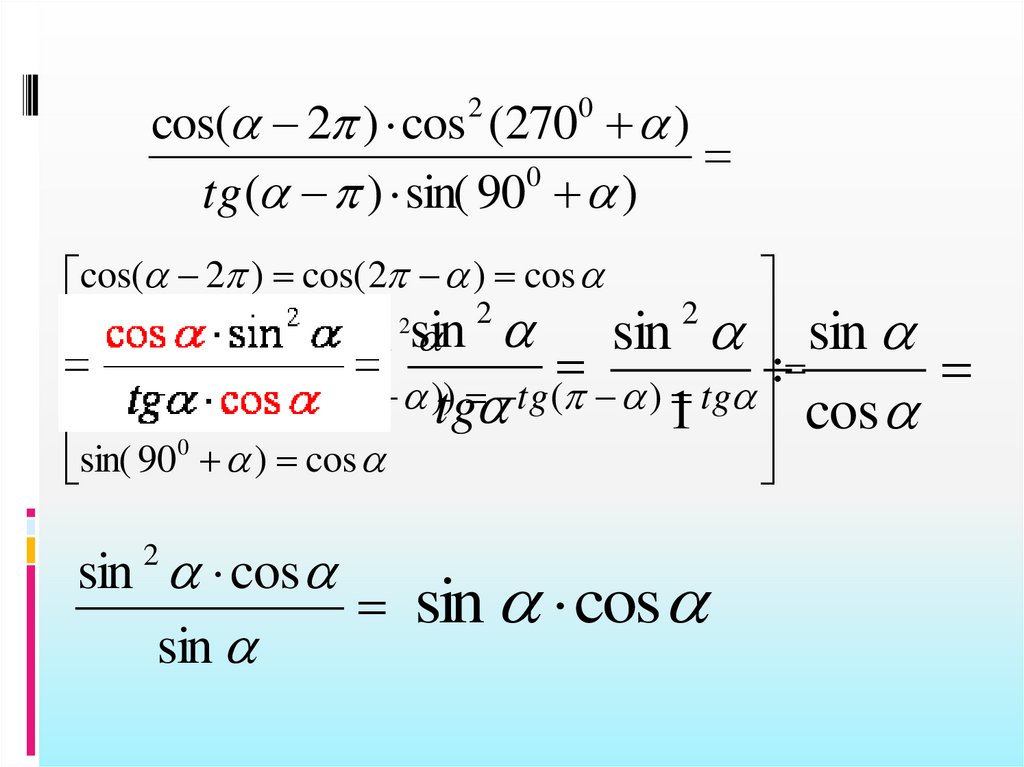


















































 mathematics
mathematics








