Similar presentations:
Возрастание и убывание функций
1.
Возрастание иубывание
функций
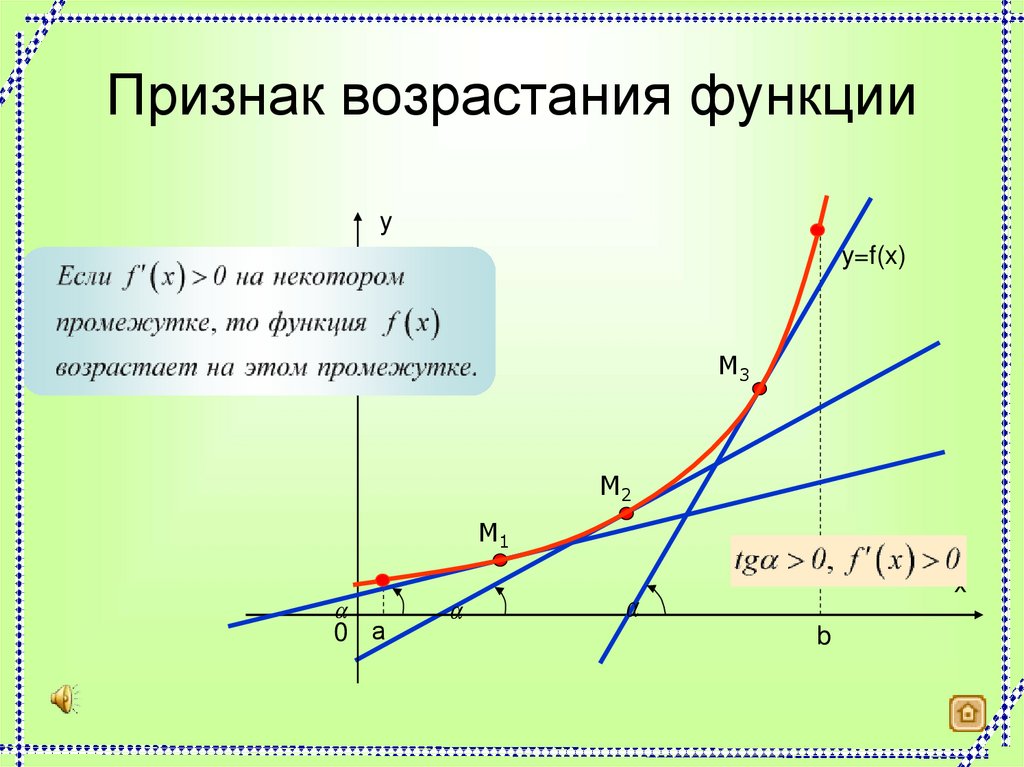
2. Признак возрастания функции
yy=f(x)
M3
M2
M1
0 а
x
b
3. Признак убывания функции
yy=f(x)
M1
M2
M3
x
0
а
b
4. Как определить промежутки убывания и возрастания функции
Алгоритм:1. Найти производную функции f'(x).
2. Найти стационарные (f'(x)=0) и критические
(f'(x) не существует) точки функции у= f(x).
3. Отметить стационарные и критические точки
на числовой прямой и определить знаки производной
на получившихся промежутках.
Пример 1
Пример 2
4. Сделать выводы о промежутках возрастания и
убывания функции.
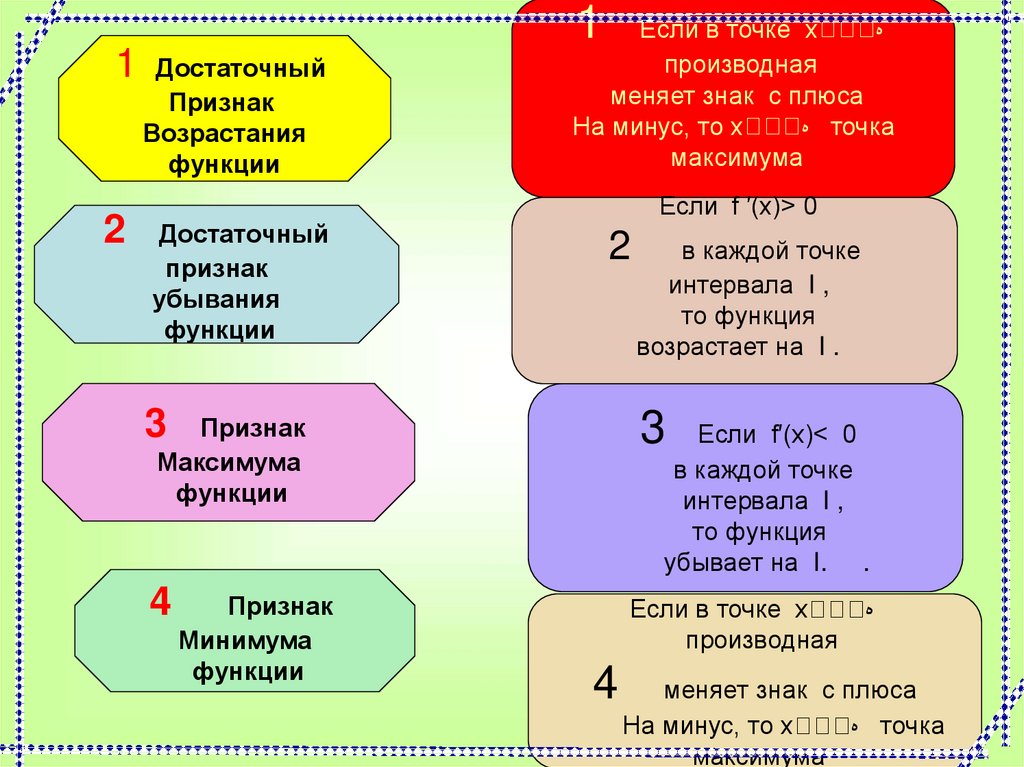
5. Как определить промежутки убывания и возрастания функции
11
2
Достаточный
Признак
Возрастания
функции
Достаточный
признак
убывания
функции
Если в точке х
производная
меняет знак с плюса
На минус, то х
точка
максимума
Если f ′(х)> 0
2
3
3
Признак
Максимума
функции
4
Признак
Минимума
функции
в каждой точке
интервала I ,
то функция
возрастает на I .
Если f′(х)< 0
в каждой точке
интервала I ,
то функция
убывает на I. .
Если в точке х
производная
4
меняет знак с плюса
На минус, то х
точка
максимума
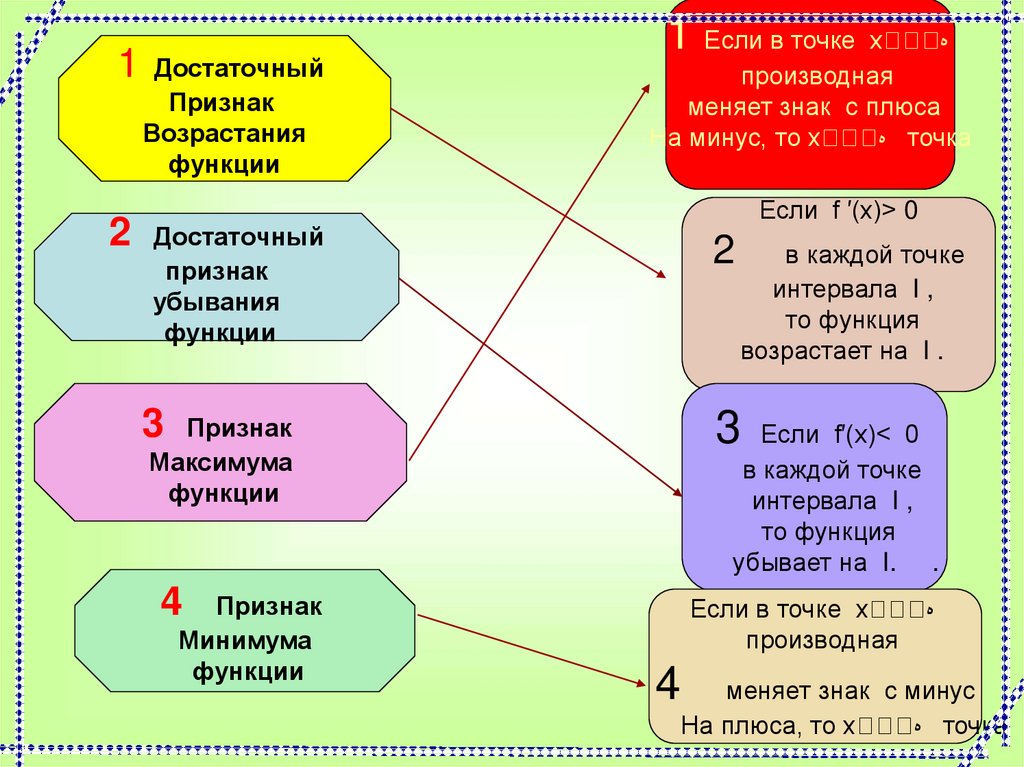
6. Как определить промежутки убывания и возрастания функции
12
Достаточный
Признак
Возрастания
функции
1 Если в точке
х
производная
меняет знак с плюса
На минус, то х
точка
Если f ′(х)> 0
Достаточный
признак
убывания
функции
2
3
3
Признак
Максимума
функции
Если f′(х)< 0
в каждой точке
интервала I ,
то функция
убывает на I. .
4
Признак
Минимума
функции
в каждой точке
интервала I ,
то функция
возрастает на I .
Если в точке х
производная
4
меняет знак с минус
На плюса, то х
точка
7. График функции
.а) у = х³ — 6 х² + 9 х — 9;
б) у = 3 х² — 5х + 4.
8. График функции
Самостоятельная работаВ-1
В-2
1) Найти промежутки возрастания и убывания
функции У = f(x).
А1
А2
3
2
f(x) = x + x + 16
f(x) = x3 + 4x2 - 37
B1
B2
f(x) = 2x4 – 4x2 +15
f(x) = x4 – 8x2



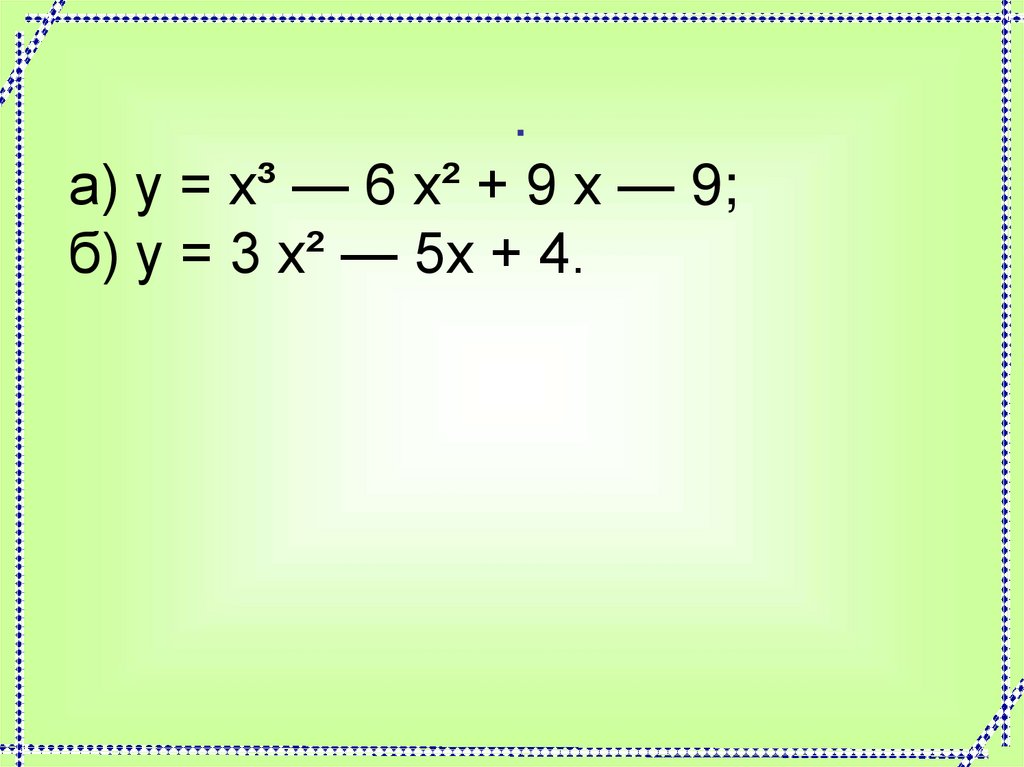

 mathematics
mathematics








