Similar presentations:
Возрастание и убывание функций
1.
Возрастание иубывание
функций
2.
Слушаю – забываю.Смотрю – запоминаю.
Делаю – понимаю.
Конфуций
3.
Изучение нового материала• Признак возрастания функции
• Признак убывания функции
• Как определить промежутки убывания и
возрастания функции
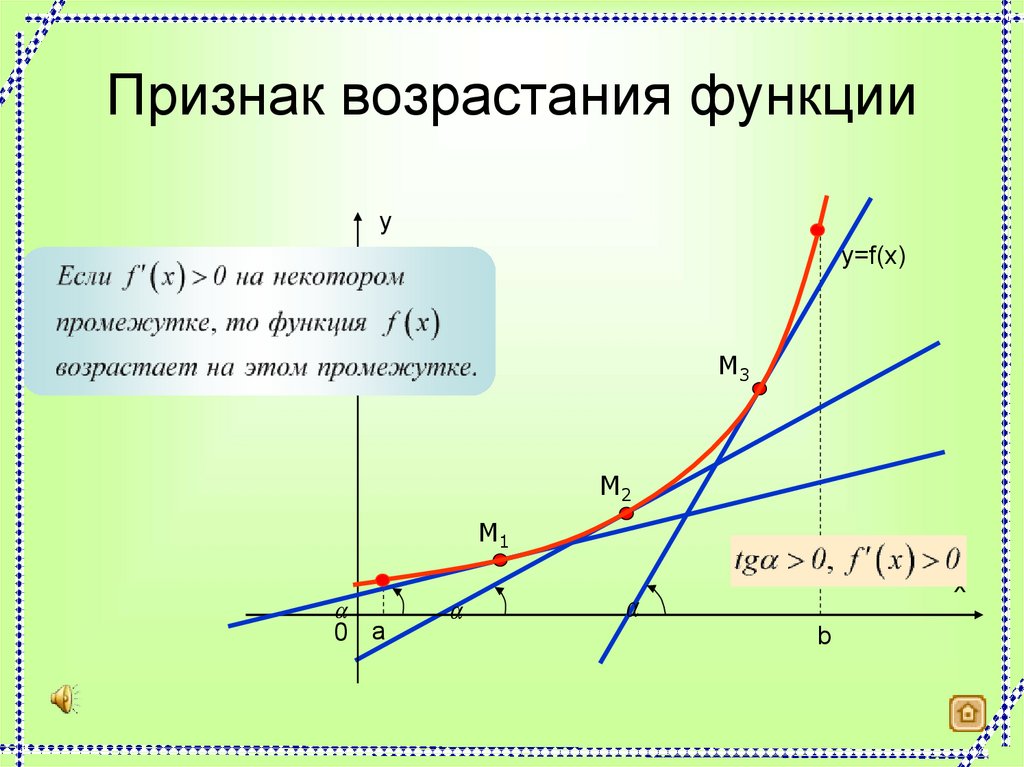
4. Признак возрастания функции
yy=f(x)
M3
M2
M1
0 а
x
b
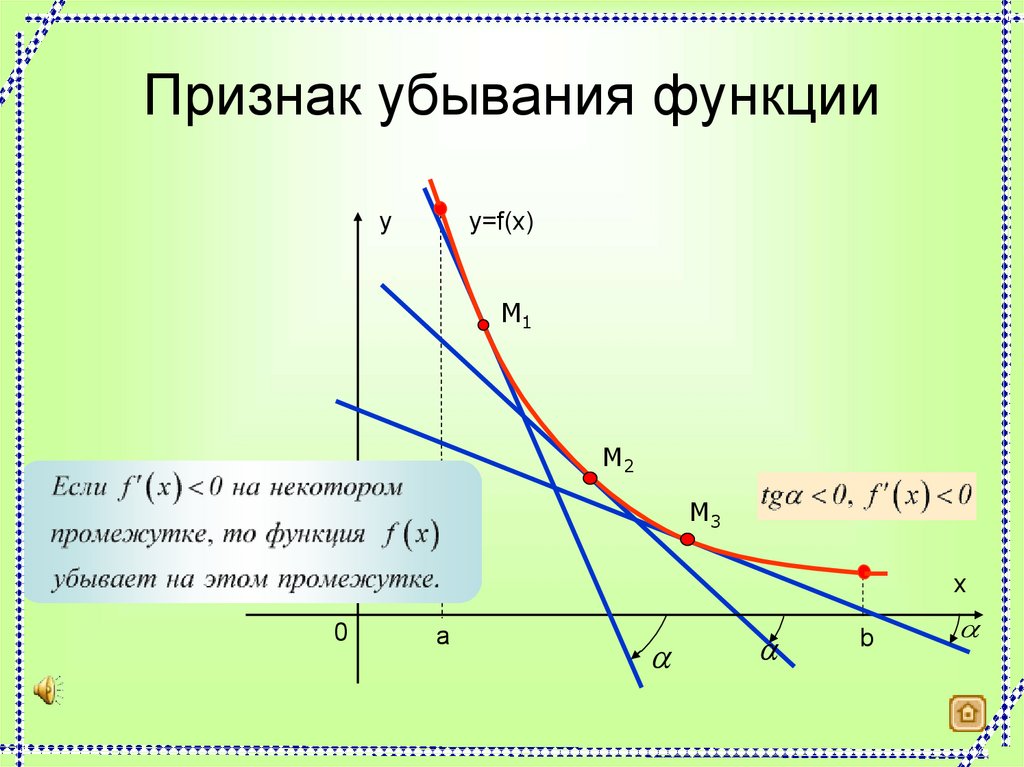
5. Признак убывания функции
yy=f(x)
M1
M2
M3
x
0
а
b
6. Как определить промежутки убывания и возрастания функции
Алгоритм:1. Найти производную функции f'(x).
2. Найти стационарные (f'(x)=0) и критические
(f'(x) не существует) точки функции у= f(x).
3. Отметить стационарные и критические точки
на числовой прямой и определить знаки производной
на получившихся промежутках.
Пример 1
Пример 2
4. Сделать выводы о промежутках возрастания и
убывания функции.
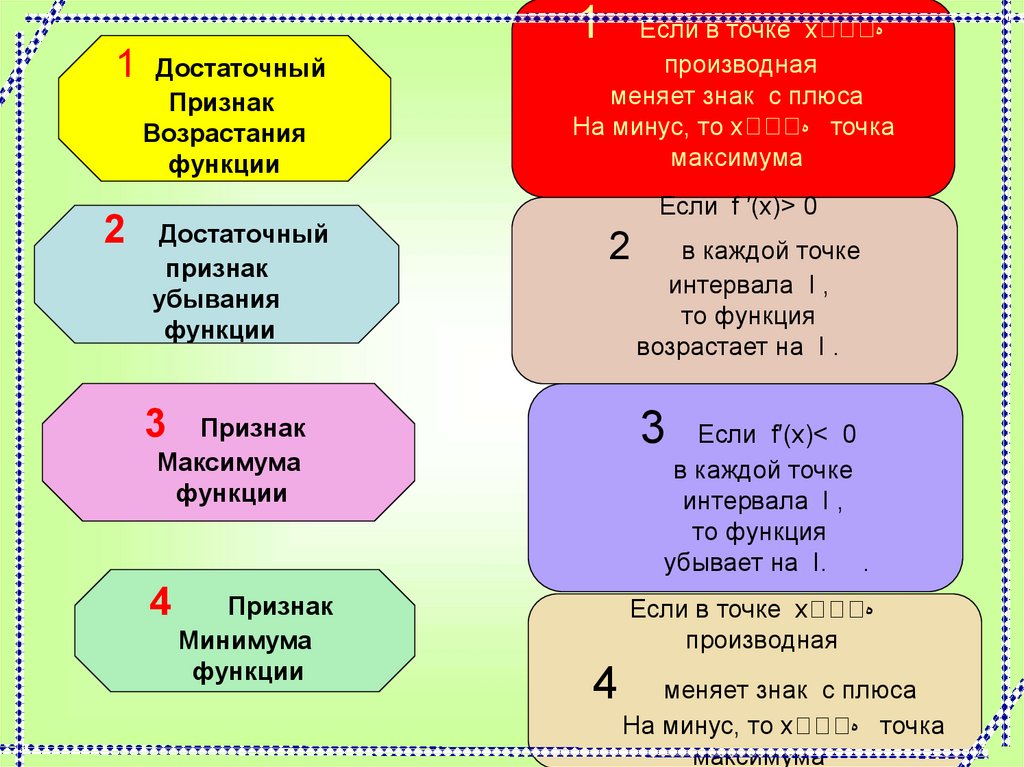
7. Как определить промежутки убывания и возрастания функции
11
2
Достаточный
Признак
Возрастания
функции
Достаточный
признак
убывания
функции
Если в точке х
производная
меняет знак с плюса
На минус, то х
точка
максимума
Если f ′(х)> 0
2
3
3
Признак
Максимума
функции
4
Признак
Минимума
функции
в каждой точке
интервала I ,
то функция
возрастает на I .
Если f′(х)< 0
в каждой точке
интервала I ,
то функция
убывает на I. .
Если в точке х
производная
4
меняет знак с плюса
На минус, то х
точка
максимума
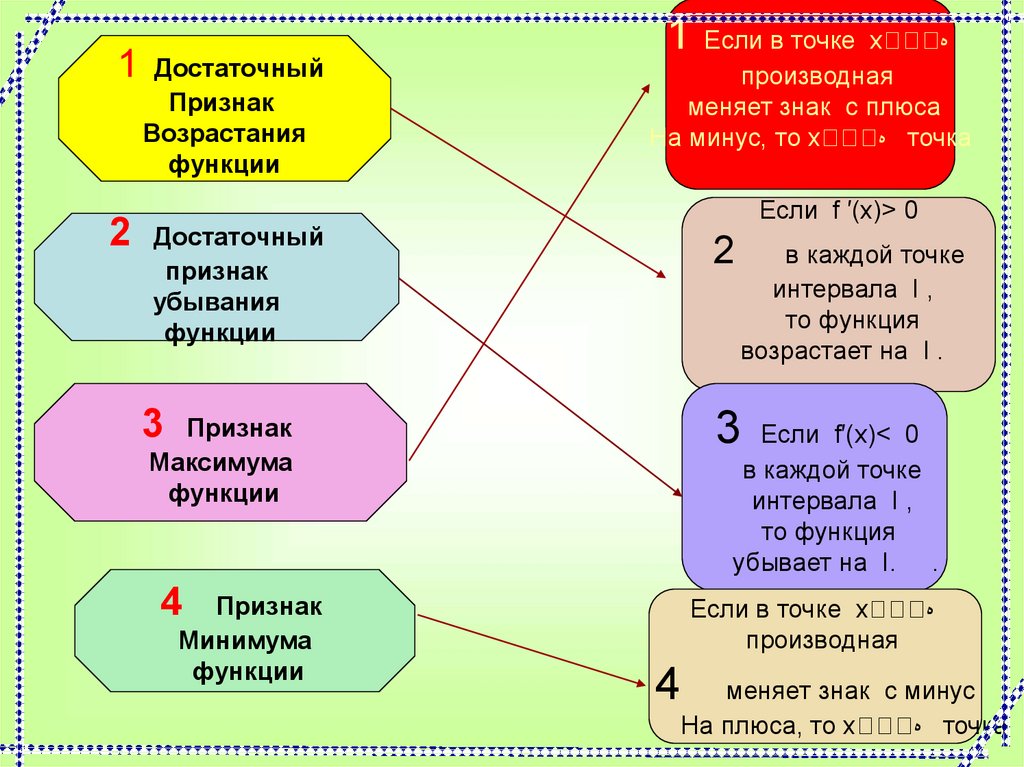
8. Как определить промежутки убывания и возрастания функции
12
Достаточный
Признак
Возрастания
функции
1 Если в точке
х
производная
меняет знак с плюса
На минус, то х
точка
Если f ′(х)> 0
Достаточный
признак
убывания
функции
2
3
3
Признак
Максимума
функции
Если f′(х)< 0
в каждой точке
интервала I ,
то функция
убывает на I. .
4
Признак
Минимума
функции
в каждой точке
интервала I ,
то функция
возрастает на I .
Если в точке х
производная
4
меняет знак с минус
На плюса, то х
точка
9. График функции
Учащиеся работают в парах,решение записывают в тетрадях.
а) у = х³ — 6 х² + 9 х — 9;
б) у = 3 х² — 5х + 4.
Двое работают у доски.
а) у = 2 х³ – 3 х² – 36 х + 40
б) у = 4х - 2 х³
10. График функции
Самостоятельная работаВ-1
В-2
1) Найти промежутки возрастания и убывания
функции У = f(x).
А1
А2
3
2
f(x) = x + x + 16
f(x) = x3 + 4x2 - 37
B1
B2
f(x) = 2x4 – 4x2 +15
f(x) = x4 – 8x2
11.
ИсаакНьютон
(1643-1727)
12.
«Варианты вопросов В изоткрытого сегмента ЕГЭ»
+
-
-
+
13.
f ( x ) 0f ( x ) 0
у f (x )
у
х
0
f ( x ) 0
у f (x)
max
у
max
0
min
min
min
х
14.
4. На рисунке изображен график производной функцииопределенной на интервале
. Найдите промежутки
убывания функции . В ответе укажите длину наибольшего из
них.
В8 6
f x0 0 функция
убывает
,
15.
7. На рисунке изображен график производной функции, определенной
на интервале
. Найдите промежутки возрастания функции
.
В ответе укажите сумму целых точек, входящих в эти промежутки.
f x0 0 функция
-1
0 1
возрастает
2 3 4
-1+0+1+2+3+4=…
В8 9
16. «Варианты вопросов В из открытого сегмента ЕГЭ»
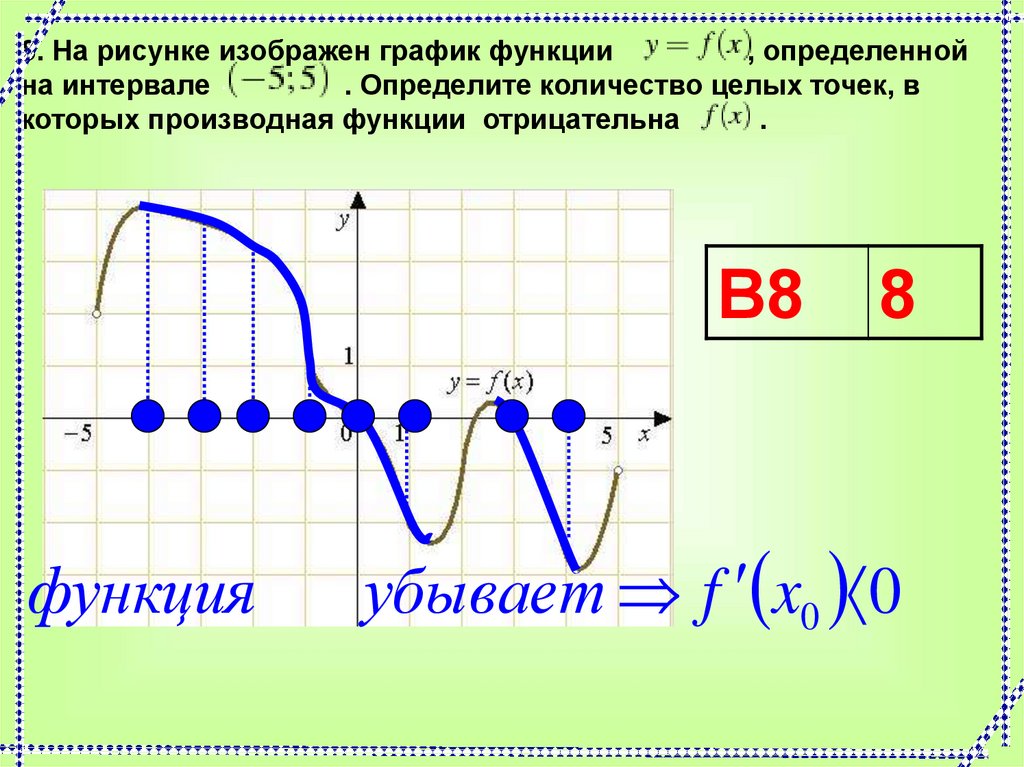
8. На рисунке изображен график функции, определенной
на интервале
. Определите количество целых точек, в
которых производная функции отрицательна
.
В8
функция
8
убывает f x0 0
17.
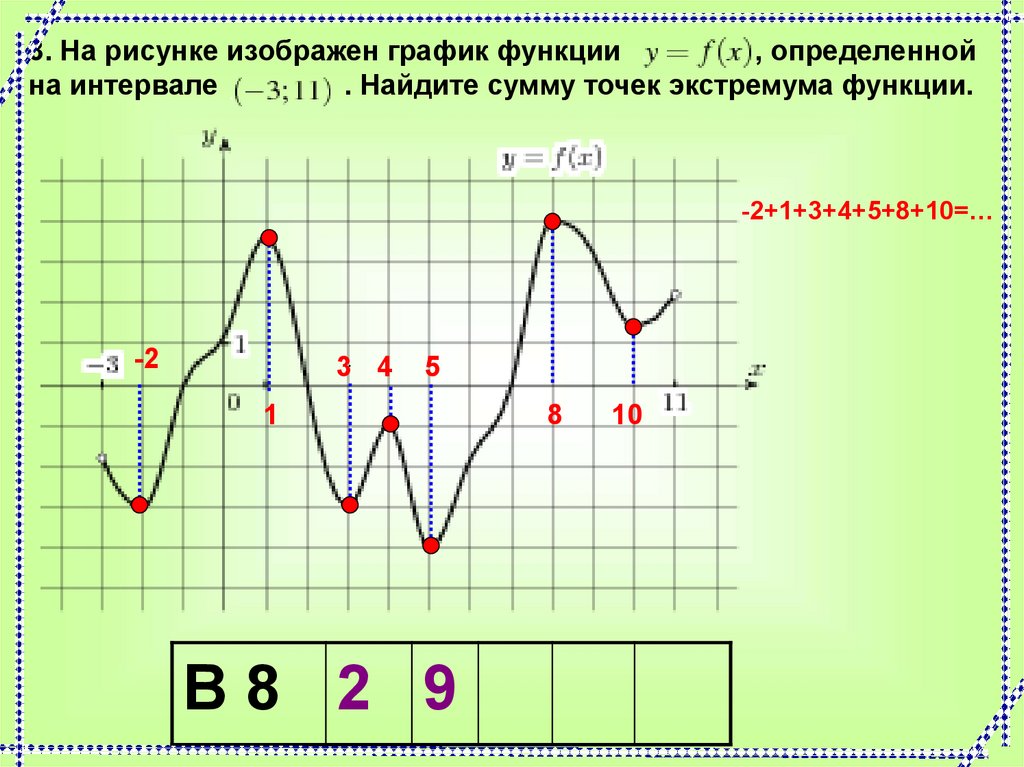
3. На рисунке изображен график функции, определенной
на интервале
. Найдите сумму точек экстремума функции.
-2+1+3+4+5+8+10=…
-2
3. 4
5
1
В8 2 9
8
10
18.
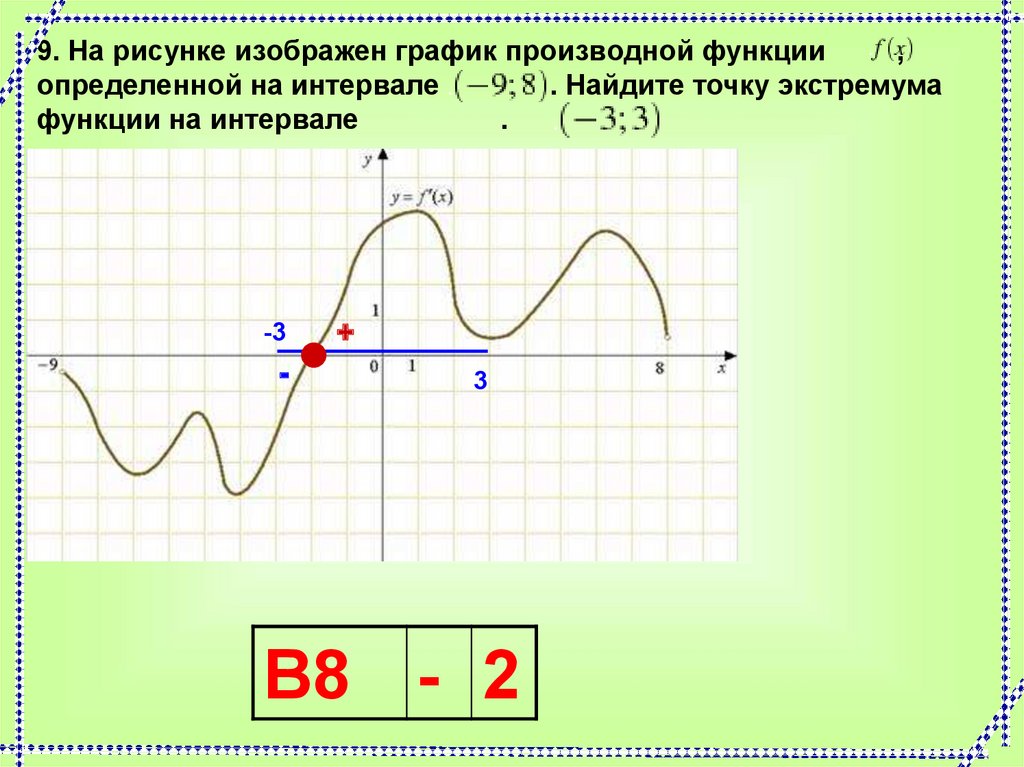
9. На рисунке изображен график производной функции,
определенной на интервале
. Найдите точку экстремума
функции на интервале
.
-3
-
+
3
В8 - 2
19.
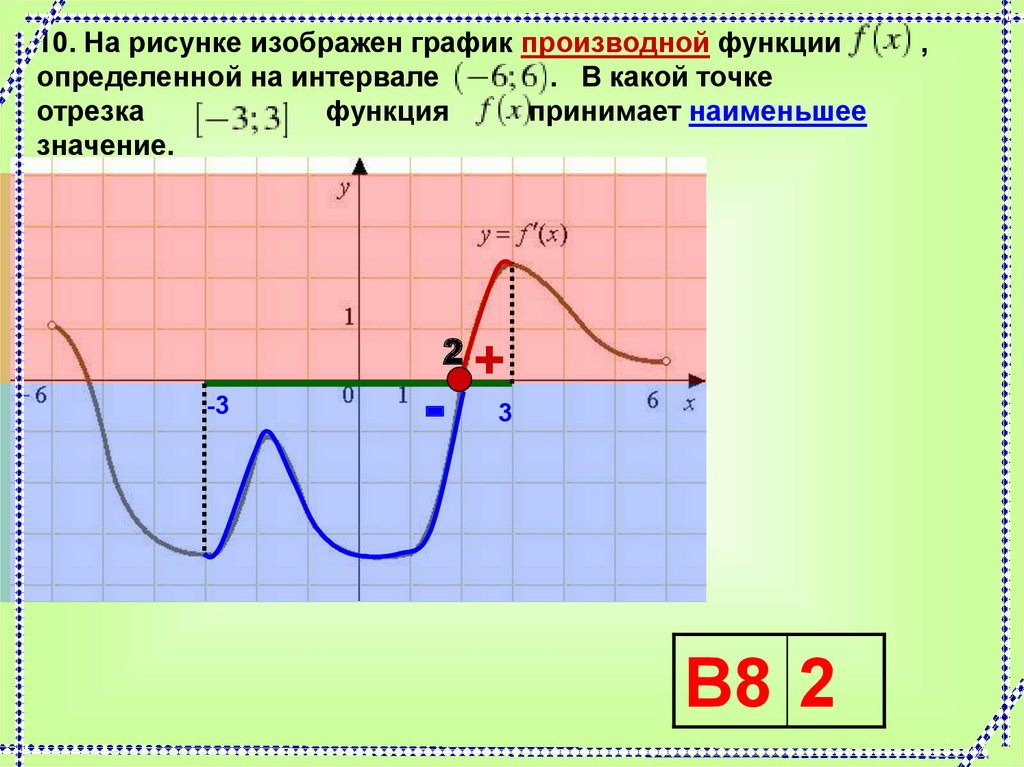
10. На рисунке изображен график производной функцииопределенной на интервале
. В какой точке
отрезка
функция
принимает наименьшее
значение.
2
-3
-
+
3
В8 2
,
20.
21.
22.
23.
24.
Я – функция сложная, это известно,Ещё расскажу, если вам интересно,
Что точку разрыва и корень имею,
И есть интервал, где расти не посмею.
Во всём остальном положительна, право,
И это, конечно, не ради забавы.
Для чисел больших я стремлюсь к единице.
Найдите меня среди прочих в таблице.
25.
26.
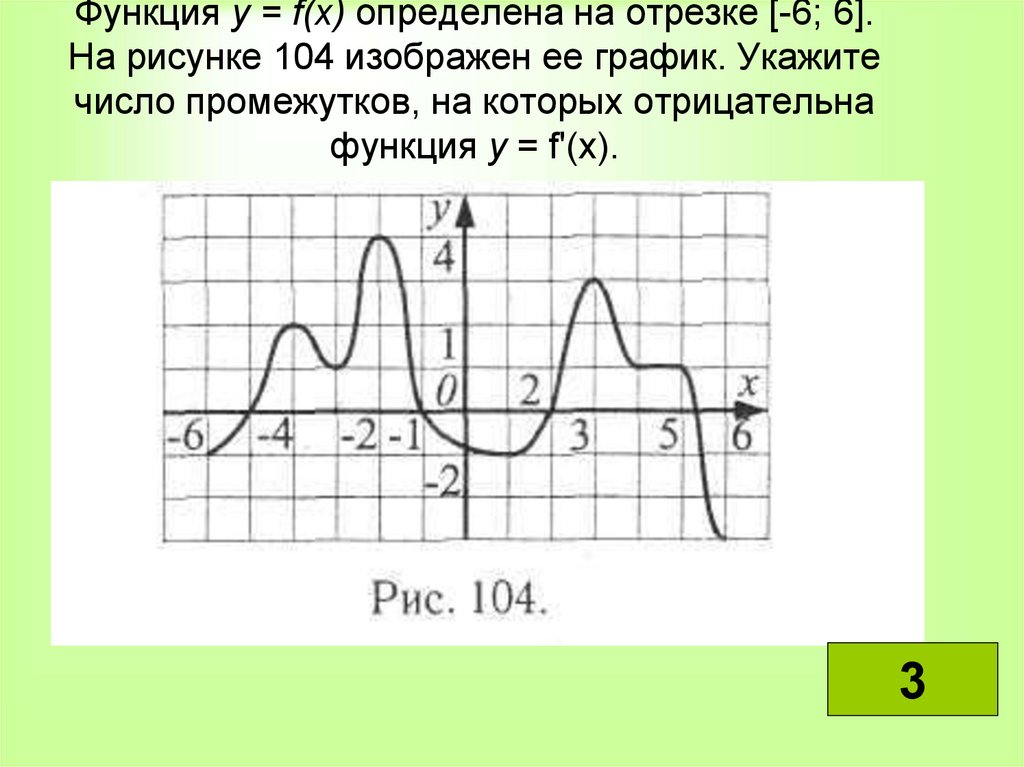
Функция у = f(x) определена на отрезке [-6; 6].На рисунке 104 изображен ее график. Укажите
число промежутков, на которых отрицательна
функция у = f'(х).
3
27.
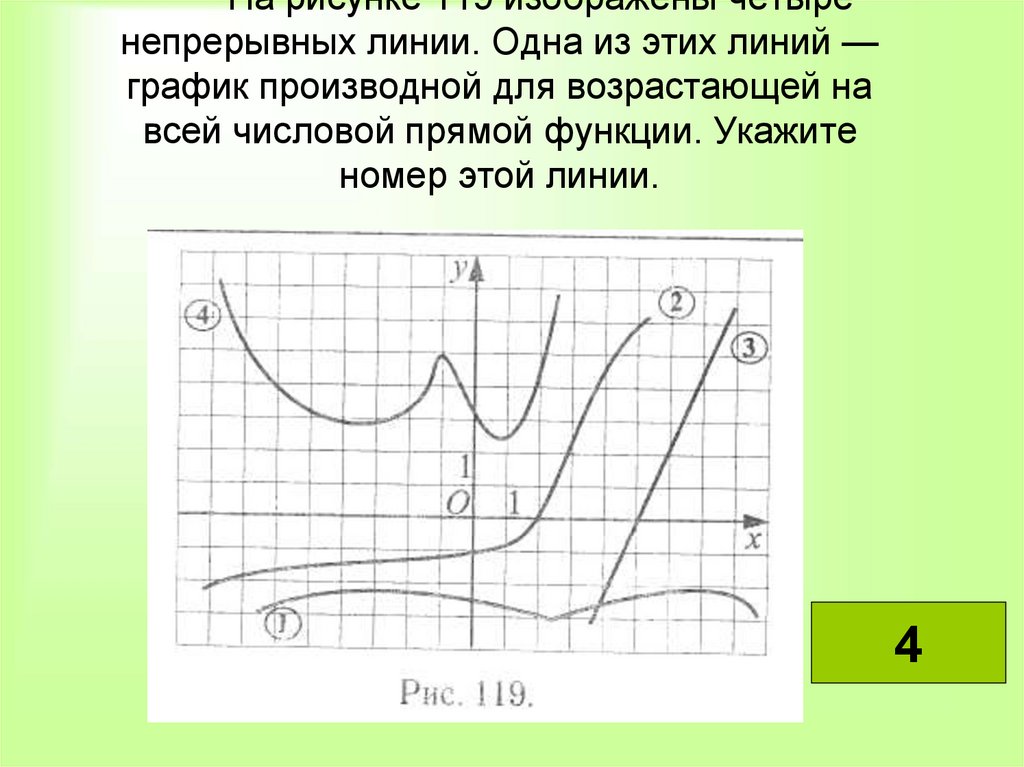
На рисунке 119 изображены четыренепрерывных линии. Одна из этих линий —
график производной для возрастающей на
всей числовой прямой функции. Укажите
номер этой линии.
4















 mathematics
mathematics








