Астродинамика. Движение космических аппаратов по орбите

1. Движение космических аппаратов по орбите (астродинамика)

ДВИЖЕНИЕ КОСМИЧЕСКИХ АППАРАТОВ ПО ОРБИТЕ
(АСТРОДИНАМИКА)
В.Н. Бранец, Р.В. Федулов
Лекция из курса «Системы управления движением,
ориентации и навигации космических аппаратов»

2. 1. Задача двух тел. Основные уравнения и параметры орбит 2. Качественный анализ орбитального движения 3. Кривизна Земли 4.

1.
2.
3.
4.
5.
2
Задача двух тел. Основные уравнения и параметры орбит
Качественный анализ орбитального движения
Кривизна Земли
Гравитационное поле Земли
Учет возмущений в вычислении орбит
Наименование события
Дата и место проведения мероприятия

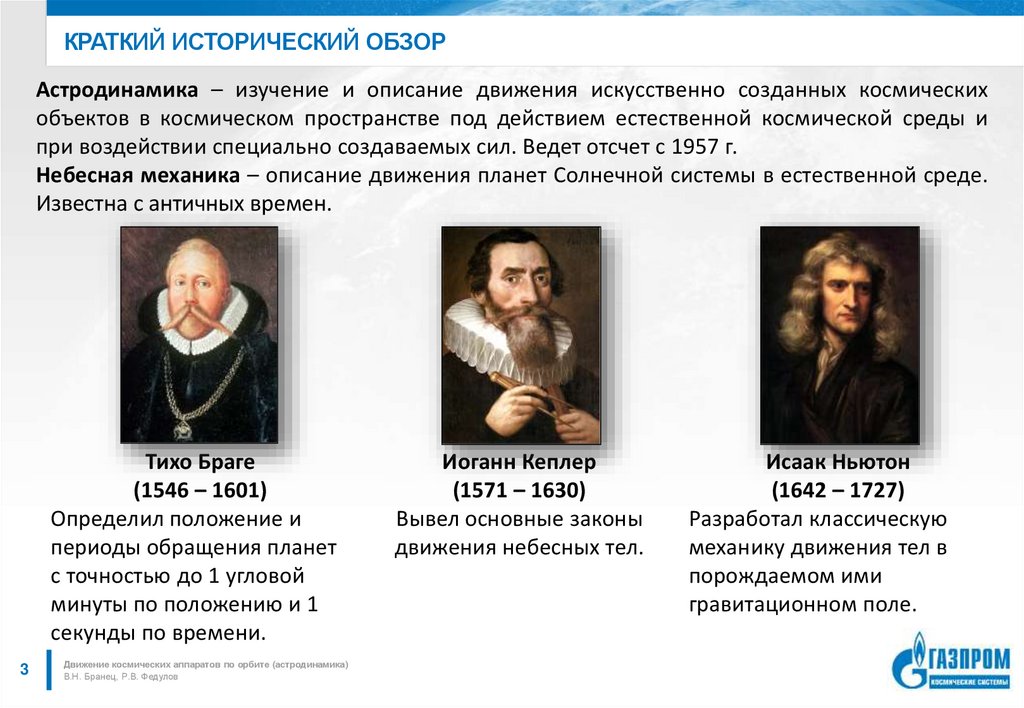
3. Краткий исторический обзор

КРАТКИЙ ИСТОРИЧЕСКИЙ ОБЗОР
Астродинамика – изучение и описание движения искусственно созданных космических
объектов в космическом пространстве под действием естественной космической среды и
при воздействии специально создаваемых сил. Ведет отсчет с 1957 г.
Небесная механика – описание движения планет Солнечной системы в естественной среде.
Известна с античных времен.
Тихо Браге
(1546 – 1601)
Определил положение и
периоды обращения планет
с точностью до 1 угловой
минуты по положению и 1
секунды по времени.
3
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Иоганн Кеплер
(1571 – 1630)
Вывел основные законы
движения небесных тел.
Исаак Ньютон
(1642 – 1727)
Разработал классическую
механику движения тел в
порождаемом ими
гравитационном поле.

4. Законы кеплера

ЗАКОНЫ КЕПЛЕРА
Первый закон Кеплера
Орбита каждого из взаимодействующих тел является коническим сечением, в фокусе
которого находится центр масс. Если тела имеют ограниченное расстояние между собой на
длительном промежутке времени, то их орбиты являются эллипсами, при неограниченном
расстоянии – это гиперболы.
Второй закон Кеплера
Линия, соединяющая два тела при вращении,
описывает равные площади в равные
промежутки времени (см. рисунок).
Третий закон Кеплера
Сумма масс двух тел, взаимно обращающихся
по эллиптической орбите, умноженная на
квадрат периода обращения пропорциональна
кубу среднего расстояния между ними.
M m T 2 ~ r 3
4
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Для просмотра анимации нажмите F5

5. уравнения задачи двух тел

УРАВНЕНИЯ ЗАДАЧИ ДВУХ ТЕЛ
Сила взаимодействия масс подчиняется закону:
F
GMmr
r3
F – сила притяжения двух объектов массами M и m
r – радиус-вектор, соединяющий их центры
G = 6,6726±0,0005·10-11 м2/кг·с2 – гравитационная постоянная
M = 5,9742·1024 кг – масса Земли
μ = G·M = 398,6005·1012 м3/с2
Уравнения движения тел идентичны:
d 2 rM
GMm
M 2 0
2
dt
r
d 2 rm
GMm
m
0
2
2
dt
r
Сокращаем массы и складываем уравнения >>>
5
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

6. Основное уравнение задачи двух тел

ОСНОВНОЕ УРАВНЕНИЕ ЗАДАЧИ ДВУХ ТЕЛ
Основное уравнение задачи двух тел (уравнение невозмущённого движения):
d 2r
3r=0
2
dt
r
μ = G(M+m) ≈ GM
Удобно ввести потенциальную функцию основной притягивающей массы:
GM
r
r
Тогда сила притяжения, действующая на единицу массы, находящейся в точке r,
вычисляется как градиент U:
U
d 2r
grad U
2
dt
Основное уравнение задачи двух тел имеет 6 интегралов.
«Интеграл» = «закон сохранения»
6
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

7. Интеграл энергии

ИНТЕГРАЛ ЭНЕРГИИ
Интеграл энергии получается умножением обеих частей основного уравнения задачи двух тел
d 2r
=
r
2
3
dt
r
скалярно на вектор скорости v =
dr
dt
2
dr d dr
dr
2r
dt dt dt
r3
dt
Интегрируем обе части:
2
dr dr
2
2
=
v
V
h
r
dt dt
2
2
где h – константа интегрирования.
Физический смысл: кинетическая энергия преобразуется в потенциальную и наоборот:
mV 2 m
mh
2
r
7
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

8. Интеграл момента количества движения (интеграл площадей)

ИНТЕГРАЛ МОМЕНТА КОЛИЧЕСТВА ДВИЖЕНИЯ (ИНТЕГРАЛ ПЛОЩАДЕЙ)
Интеграл момента количества движения (интеграл площадей) получается векторным
умножением обеих частей основного уравнения задачи двух тел на r:
d 2r
=
r
2
3
dt
r
d 2 r d dr
r 2 = r = 0
dt
dt
dt
Интегрируем обе части:
dr
r v = c
dt
где с – константа интегрирования, имеющая размерность момента импульса (количества
движения). Следовательно, r(t) изменяется, оставаясь в неподвижной плоскости,
перпендикулярной c. Физический смысл: в задаче двух тел плоскость орбиты сохраняет своё
положение в пространстве.
c
v
r
r
c
r
8
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
v

9. Интеграл лапласа

ИНТЕГРАЛ ЛАПЛАСА
Интеграл Лапласа получается векторным умножением обеих частей основного уравнения
задачи двух тел на c:
d 2r
=
r
2
3
dt
r
d 2r
c
=
r c
2
3
dt
r
d 2r
dr
c
=
r r
2
3
dt
r
dt
d 2r
2 dr dr
c
=
r
r r
dt 2
r 3 dt dt
d 2r
d r
c
=
dt 2
dt r
т.к.
9
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
d 1
1 dr
r dr
dt r
r 2 dt
r 3 dt

10. Интеграл лапласа

ИНТЕГРАЛ ЛАПЛАСА
Интегрируя обе части, получим
dr
r
c f
dt
r
где f – константа интегрирования (вектор Лапласа).
Можно видеть, что c·f = 0, т.е. вектор f лежит в плоскости орбиты.
Умножая обе части уравнения скалярно на r, получим
dr
r
r c r f
dt
r
dr
r c = r f r
dt
c2 r f r
Это равенство называется интегралом Лапласа.
10
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

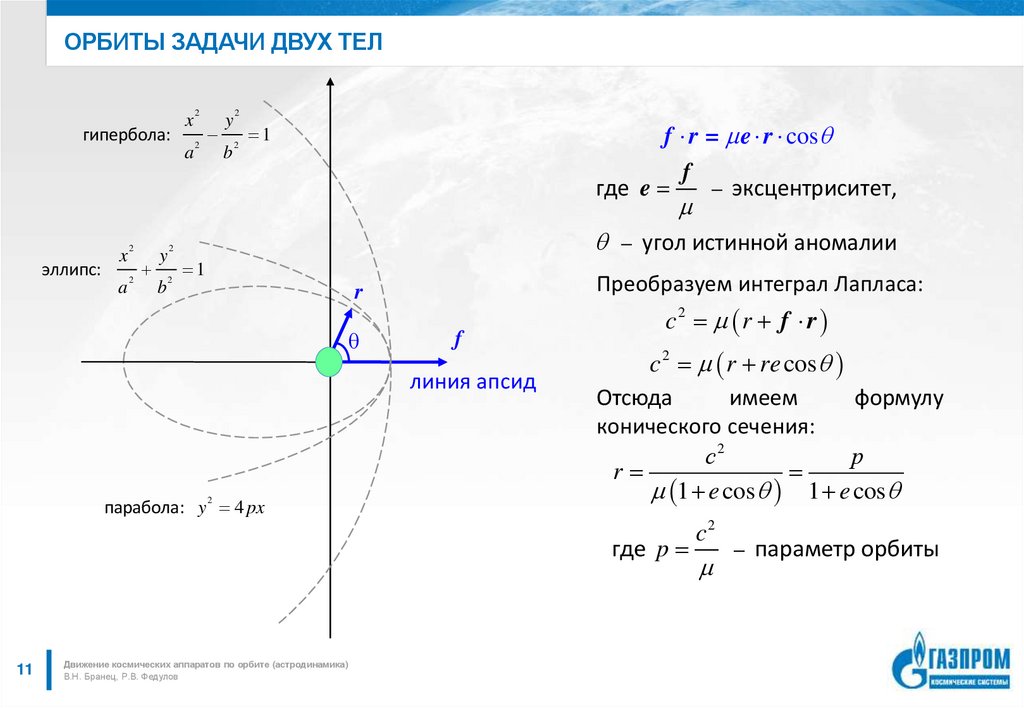
11. Орбиты задачи двух тел

ОРБИТЫ ЗАДАЧИ ДВУХ ТЕЛ
гипербола:
эллипс:
x
2
a
2
y
2
b
2
x
2
a
2
y
2
b
2
f r = e r cos
f
где e
эксцентриситет,
1
1
Преобразуем интеграл Лапласа:
r
θ
f
линия апсид
парабола: y 4 px
2
угол истинной аномалии
c2 r f r
c 2 r re cos
Отсюда
имеем
формулу
конического сечения:
с2
p
r
1 e cos 1 e cos
где p
11
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
c2
параметр орбиты

12. Конические сечения

КОНИЧЕСКИЕ СЕЧЕНИЯ
Окружность:
a b 0, e 0
Эллипс:
b2
a b 0, e 1 2
a
2
Парабола:
a , e 1
Гипербола:
b2
a 0, e 1 2
a
2
Эллипс
12
Парабола
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Гипербола

13. Эллиптическая орбита

ЭЛЛИПТИЧЕСКАЯ ОРБИТА
e
ra rp
ra a 1 e
b
a
ra rp
a
b
rp a 1 e
b2
p
a 1 e 2
a
b a 1 e2
a – большая полуось;
b – малая полуось;
ra – расстояние от фокуса до апоцентра орбиты;
rp – расстояние от фокуса до перицентра орбиты.
13
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

14. Интегралы площадей и энергии через параметры орбиты

ИНТЕГРАЛЫ ПЛОЩАДЕЙ И ЭНЕРГИИ ЧЕРЕЗ ПАРАМЕТРЫ ОРБИТЫ
Тангенциальная компонента скорости:
v
v
d
2
2 2
V 2 Vr 2 V 2 r r
r r
dt
d
c r v = rV r 2
r 2
dt
c c
V r 1 e cos
r p
2
2
vr
c
r
v
Дифференцируя формулу конического сечения, получим радиальную компоненту скорости:
dr
p
pe sin 2
ec
Vr
e
sin
r
sin
2
2
dt
p
p
1 e cos
Складывая радиальную и тангенциальную компоненту скорости, получим:
2
ec
c2
c2
2
2
2
2
V Vr V sin 2 1 e cos 2 1 2e cos e2
p
p
p
14
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

15. Интеграл энергии через параметры орбиты

ИНТЕГРАЛ ЭНЕРГИИ ЧЕРЕЗ ПАРАМЕТРЫ ОРБИТЫ
Для определения константы интегрирования h интеграла энергии возьмем на орбите точку
θ=0. Для этой точки r=p/(1+e). В этой точке квадрат скорости будет равен
2
c
c
2
2
2
1
2
e
e
1
e
1
e
p2
p
p
2
2
2
h V 2
1 e
1 e 2
r
p
r
p
a
V2
2
В зависимости от типа конического сечения интеграл энергии выражается следующим
образом:
2 1
r a для эллипса
2
V2
для параболы
r
2
h
для гиперболы
r
15
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

16. Шестой интеграл – время прохождения перицентра

ШЕСТОЙ ИНТЕГРАЛ – ВРЕМЯ ПРОХОЖДЕНИЯ ПЕРИЦЕНТРА
Радиус-вектор заметает площадь А с секторной скоростью
dA r 2 d 1 2
c
r
dt
2 dt 2
2
С другой стороны, площадь эллипса равна πab, т.е. секторная скорость равна площади,
деленной на период обращения T:
dA ab
dt
T
3
2
2 ab 2 a a 1 e
2 a 1 e
2 a 1 e
2 a
a3
T
2
2
c
c
p
a 1 e
2
Из верхнего уравнения следует:
2
2
2
2
d 2 d
p2
dt
r
c
c 1 e cos 2
При интегрировании определится последняя шестая константа, являющаяся временем τ
прохождения перицентра орбиты:
p2
d
t
τ
2
c 0 1 e cos
16
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

17. Итого Шесть интегралов

ИТОГО ШЕСТЬ ИНТЕГРАЛОВ
1. Интеграл энергии;
2. Интеграл вектора количества движения c = (cx; cy; cz) – три параметра;
3. Вектор Лапласа f, задающий положение большой полуоси;
4. Время τ прохождения заданной точки орбиты.
Векторы с и f задают положение плоскости орбиты в пространстве.
Параметры a/p/T задают форму орбиты.
Параметр τ определяет время прохождения заданной точки орбиты.
17
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

18. Кеплеровы элементы Орбиты

КЕПЛЕРОВЫ ЭЛЕМЕНТЫ ОРБИТЫ
i – наклонение плоскости орбиты к
экватору;
Ω – долгота восходящего узла – угол,
отсчитываемый от линии весеннего
равноденствия до точки пересечения
орбиты с экватором при движении КА из
южного полушария в северное;
ω – аргумент перицентра, измеряемый
против часовой стрелки от восходящего
узла в плоскости орбиты;
a или p – главная полуось орбиты или
полуфокальный параметр;
e – эксцентриситет;
θ, M, τ – истинная, средняя аномалии,
задающие положение КА относительно
перицентра, и время прохождения
перицентра.
18
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

19. Орбитальные аномалии для эллиптической орбиты

ОРБИТАЛЬНЫЕ АНОМАЛИИ ДЛЯ ЭЛЛИПТИЧЕСКОЙ ОРБИТЫ
Истинная аномалия θ – действительное
угловое положение КА на орбите.
Простого аналитического соотношения
для ее нахождения не существует.
Средняя аномалия M – отсчитываемое от
перицентра
угловое
положение
гипотетического тела, движущегося с
постоянной угловой скоростью
по
круговой орбите:
2
M
t
T
T – период обращения;
Δt – время от прохождения перицентра.
Также M равна произведению среднего
движения на время:
M n t
Для просмотра анимации нажмите F5
19
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Эксцентрическая аномалия E – угол COS.

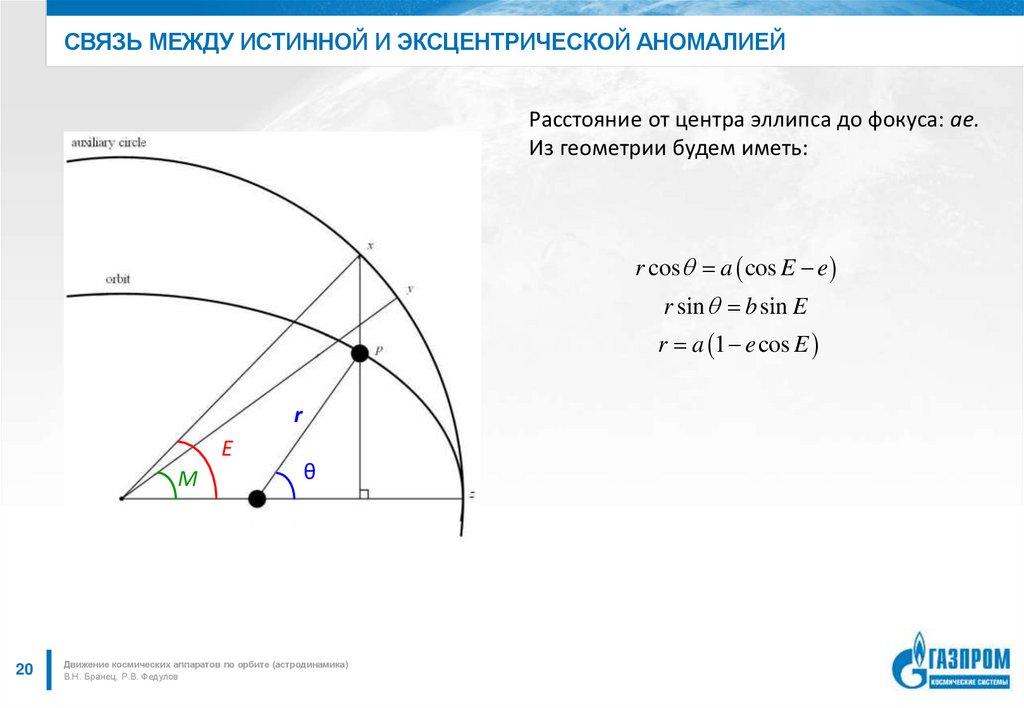
20. Связь между истинной и эксцентрической аномалией

СВЯЗЬ МЕЖДУ ИСТИННОЙ И ЭКСЦЕНТРИЧЕСКОЙ АНОМАЛИЕЙ
Расстояние от центра эллипса до фокуса: ae.
Из геометрии будем иметь:
r cos a cos E e
r sin b sin E
r a 1 e cos E
r
E
M
20
θ
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

21. Вывод Уравнения кеплера

ВЫВОД УРАВНЕНИЯ КЕПЛЕРА
Интеграл площадей:
d
p a 1 e 2
dt
Интеграл энергии для эллиптической орбиты:
r2
dr
d
2 1
V r2
dt
dt
r a
Подставляя производную истинной аномалии по времени из первого уравнения во второе,
получаем:
2
2
2
a 1 e
dr
r2
dt
Средняя угловая скорость движения:
2
2
2 1
r
n
a
2 2
2
a
e
a
r
2
r a
2
3
T
a
Тогда уравнение преобразуется к виду:
dr an 2 2
2
a e a r
dt
r
21
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

22. Уравнение кеплера

УРАВНЕНИЕ КЕПЛЕРА
ndt
rdr
a a e a r
2 2
Интегрируем:
2
1 e cos E dE
n t t0 E E0 e sin E sin E0
M E sin E
Это уравнение называется уравнением Кеплера. Оно не имеет решения в элементарных
функциях.
Схема решения простых задач
1.Для заданных r и θ найти t: по r и θ находим Е, затем М, после чего t.
2.Для заданного t найти r и v: по t находится М, затем методом итераций находится Е:
En+1=En+M, и затем определяются искомые величины.
Для круговых орбит, для которых e мало, истинная аномалия может быть выражена в виде
ряда как функция M:
5
θ M 2e sin M e 2 sin 2M ...
4
22
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

23. Задача: Определение движения по начальным условиям

ЗАДАЧА: ОПРЕДЕЛЕНИЕ ДВИЖЕНИЯ ПО НАЧАЛЬНЫМ УСЛОВИЯМ
Дано: r0(t0), v0(t0).
Найти: положение и форму орбиты, координаты и скорость тела на орбите.
Сразу можем найти постоянную момента количества движения: c = r0 x v0
Тогда параметр орбиты
2
p
c
Введем правую систему координат: ix, iy, iz такую, что
ix, iy – лежат в плоскости орбиты,
ix – направлена на перицентр,
iz – нормальна к плоскости орбиты (с положительного направления iz орбитальное движение
происходит против часовой стрелки).
Vr v
r dr
pe sin
ec sin
r dt 1 e cos 2
p
V r
c c
1 e cos
r p
Из этих формул следуют равенства для момента t0 с учетом p
23
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
c2

24. Определение орбиты

ОПРЕДЕЛЕНИЕ ОРБИТЫ
На момент t0 будем иметь:
e sin 0
c r0 v 0
r0
e cos 0
c
2
r0
Делим на μ, возводим в квадрат, складываем уравнения и получаем эксцентриситет орбиты:
2
c2
c
2
e
1
r
v
0 0
r
r
0 0
Единичный вектор ix (в направлении перицентра) равен
2
1
1 2
v
r
r
v
v
r0 cos 0 i z r0 sin 0
0 0 0
r0
e 0 r0 0
Итак, найдены величины:
c, iz – определяют плоскость орбиты;
ix, iy – определяют положение орбиты в плоскости;
p, e – определяют форму орбиты;
Таким образом, орбита определена полностью. Найдём положение и скорость тела на орбите.
ix
24
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

25. Положение и скорость тела на орбите

ПОЛОЖЕНИЕ И СКОРОСТЬ ТЕЛА НА ОРБИТЕ
Радиус-вектор тела найдется из геометрии с учетом формулы конического сечения:
p
r = r cos i x r sin i y
ix cos i y sin
1 e cos
Дифференцируя это соотношение и принимая во внимание выражения для радиальной и
тангенциальной компоненты скорости, получаем скорость в тех же координатах:
i x sin i y cos e
v=
p
Последние два уравнения справедливы, в том числе и для начальной точки движения, что
позволяет определить вектора через начальные значения скорости и положения
e cos 0
r sin 0
sin 0
r cos 0
ix
r0 0
v0 ,
iy
r0 0
v0
p
p
p
p
Подставляя это в выражения для векторов положения и скорости, получаем следующие
зависимости текущих векторов положения и скорости в функции от истинной аномалии:
r
rr
r = 1 1 cos( 0 ) r0 0 sin( 0 ) v 0
p
p
r v
r
1
v 0 0 1 cos( 0 )
sin( 0 ) r0 1 0 1 cos 0 v 0
r0 p
p
pr0
Истинная аномалия вычисляется разложением в ряд (см. выше), где M – линейная функция
времени.
25
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

26. формулы Бэттина

ФОРМУЛЫ БЭТТИНА
Ричард Бэттин предложил формулы для текущих значений
положения и скорости на эллиптической орбите, справедливые
для любых орбит и эксцентриситетов:
E E0 sin E E0
a
r = 1 1 cos E E0 r0 t
v0
3
a
r0
a
a
v
sin E E0 r0 1 1 cos E E0 v 0
rr0
r
Уравнение Кеплера, по которому для заданного времени
необходимо определить соответствующую ему эксцентрическую
аномалию:
a
t E E0
3
r0 v 0
r
1 cos E E0 1 0 sin E E0
a
a
Решение этого уравнения находится методом последовательных
итераций:
En 1 En
26
dE
tn 1 tn
dt
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Ричард Бэттин (1925 – 2014)
главный конструктор
навигационных систем
кораблей «Аполлон»,
директор программы
«Аполлон», профессор
аэронавтики и астронавтики
Массачусетского
технологического института.

27. Качественный анализ орбитального движения

КАЧЕСТВЕННЫЙ АНАЛИЗ ОРБИТАЛЬНОГО ДВИЖЕНИЯ
Рассматривая формулу для скорости тела на эллиптической орбите
2 1
V2
r a
можно видеть, что минимальной по затратам скоростью, сообщаемой КА ракетой-носителем,
является скорость на круговой орбите на минимальной высоте. Положив в уравнении r = a,
получим
V
r
Эта скорость называется первой космической.
27
Планета
1-я косм. скорость
Меркурий
3 км/с
Венера
7,3 км/с
Земля
7,9 км/с
Марс
3,6 км/с
Юпитер
42,2 км/с
Сатурн
25,1 км/с
Луна
1,7 км/с
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Вторая космическая скорость – это
минимальная скорость ухода от планеты.
Если в формуле для скорости тела положить
большую полуось, равной бесконечности,
получим
V2 2 V1

28. Мгновенный Импульс по направлению скорости

МГНОВЕННЫЙ ИМПУЛЬС ПО НАПРАВЛЕНИЮ СКОРОСТИ
V V
Дифференцируя по времени интеграл энергии, получим:
da
2VdV 2
a
Разделив это выражение на выражение для интеграла
энергии, принимая r = a, будем иметь:
2
dV da
V
a
Пусть орбита имеет радиус 6600 км и круговую скорость
8 км/с. Тогда если изменение скорости происходит на
1 м/с, что составляет 1/8000 = 1,25·10-4, то
соответствующее
увеличение
высоты
составит
2,5·10-4·6600 км = 1,65 км. Такое же уменьшение скорости
(импульс гашения скорости) приведет к такому же
изменению высоты орбиты, но в сторону ее уменьшения.
Посадочный импульс изменения скорости порядка 100
м/сек понижает высоту орбиты в противоположной точке
примерно на 170 км, захват атмосферой КА происходит
на высоте примерно 100 км.
28
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

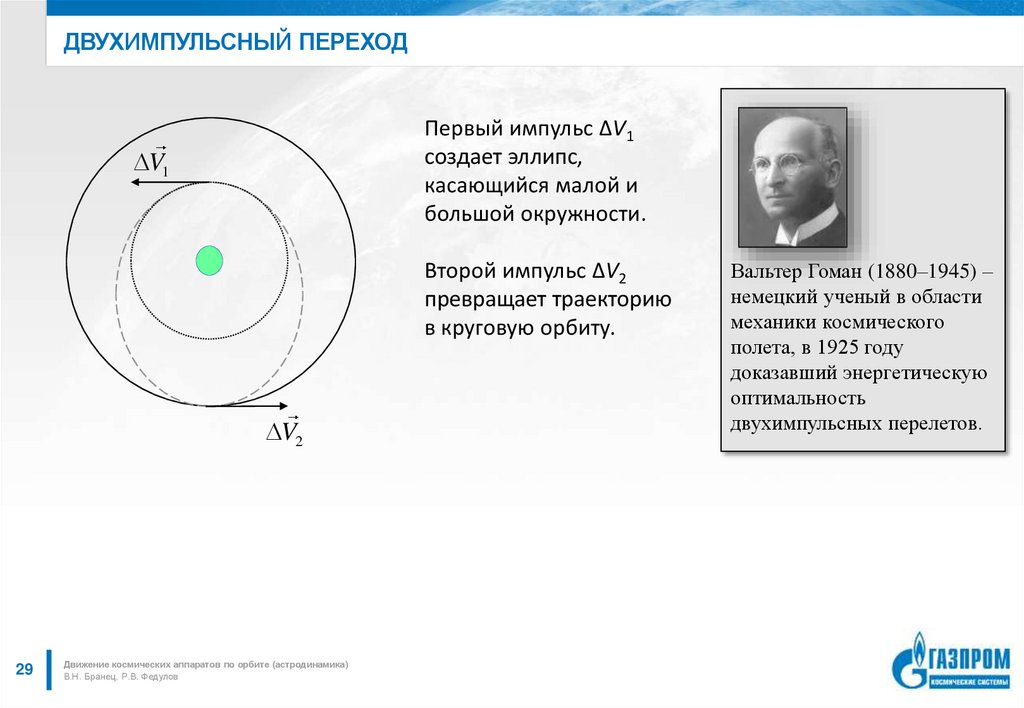
29. двухимпульсный переход

ДВУХИМПУЛЬСНЫЙ ПЕРЕХОД
Первый импульс ΔV1
создает эллипс,
касающийся малой и
большой окружности.
V1
Второй импульс ΔV2
превращает траекторию
в круговую орбиту.
V2
29
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Вальтер Гоман (1880–1945) –
немецкий ученый в области
механики космического
полета, в 1925 году
доказавший энергетическую
оптимальность
двухимпульсных перелетов.

30. Изменение наклонения орбиты

ИЗМЕНЕНИЕ НАКЛОНЕНИЯ ОРБИТЫ
V
V
1
Рассмотрим задачу изменения наклонения орбиты. Чтобы
выполнить эту операцию, нужно выдать импульс изменения
скорости в восходящем узле орбиты. Из векторного
треугольника сложения скоростей видно, что для изменения
наклонения даже на один градус нужно выдать импульс по
нормали к плоскости орбиты в этой точке величиной
V 8000 tg1 140 м/с
По этой причине формирование плоскости орбиты, как
правило, возлагается на этап выведения КА, а все
орбитальные операции выполняются на компланарных
орбитах.
К примеру, задача сближения транспортного корабля со
станцией предполагает, что старт корабля и его выведение на
промежуточную орбиту ожидания выполняется в тот момент
времени, когда точка старта на поверхности Земли проходит
через плоскость орбиты цели.
30
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

31. Схема выведения «Ямал-300К» на геостационарную орбиту

СХЕМА ВЫВЕДЕНИЯ «ЯМАЛ-300К» НА ГЕОСТАЦИОНАРНУЮ ОРБИТУ
Для просмотра анимации нажмите F5
Ракета-носитель выводит КА с разгонным блоком на низкую орбиту c наклонением 51,4°.
Затем разгонный блок серией импульсов по направлению орбитальной скорости формирует
сильно вытянутую эллиптическую орбиту так, чтобы ее апогей находился в плоскости экватора
на высоте геостационарного спутника (36 тыс. км). Орбитальная скорость в апогее
уменьшается пропорционально расстоянию, т.е. примерно в 5 раз, соответственно,
уменьшается импульс скорости, необходимый для того, чтобы «повернуть» эту скорость в
плоскость экватора. Импульс коррекции направления скорости совмещается со вторым
импульсом превращения эллиптической орбиты в круговую.
31
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

32. Межпланетные перелеты

МЕЖПЛАНЕТНЫЕ ПЕРЕЛЕТЫ
Уход с орбиты Земли требует приращения скорости как минимум
V V2 V1 1 2 V1 3, 2 км/с
Если интегралу энергии придать вид
V2
r
2
r
a
то можно видеть, что второе слагаемое при a >> r (2a – расстояние до орбиты назначения) не
влияет существенно на энергетику полета.
Энергия межорбитального перелета будет определяться скоростью ухода от Земли и
скоростью перелета от орбиты Земли к орбите планеты.
При подлете к планете назначения нужно опять затратить энергию перехода – уменьшения
скорости, чтобы перейти к эллиптической орбите около этой планеты, и, возможно, энергию
для формирования орбиты требуемого радиуса.
32
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

33. Характеристическая скорость

ХАРАКТЕРИСТИЧЕСКАЯ СКОРОСТЬ
Характеристическая скорость миссии – это суммарное изменение скорости КА, которое
требуется для выполнения его миссии. Для корабля «Союз-ТМА» характеристическая скорость
миссии составляет 280–300 м/с для орбитального участка полета.
Характеристическая скорость миссии – это величина, на которою КА должен увеличить свою
скорость для проведения необходимых операций.
Характеристическая скорость КА – это возможная величина суммарного маневра по
изменению скорости с использованием своей двигательной установки и запасов топлива.
Характеристическая скорость корабля «Союз-ТМА» составляет 350–400 м/с.
Характеристическая скорость КА – это величина, на которою КА может увеличить свою
скорость.
Характеристическая скорость корабля выбирается больше скорости миссии, что позволяет в
реальном полете иметь запас топлива на повторение некоторых операций при нештатных
ситуациях. Достижение большой характеристической скорости КА возможно с помощью
использования многоступенчатых конструкций.
33
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

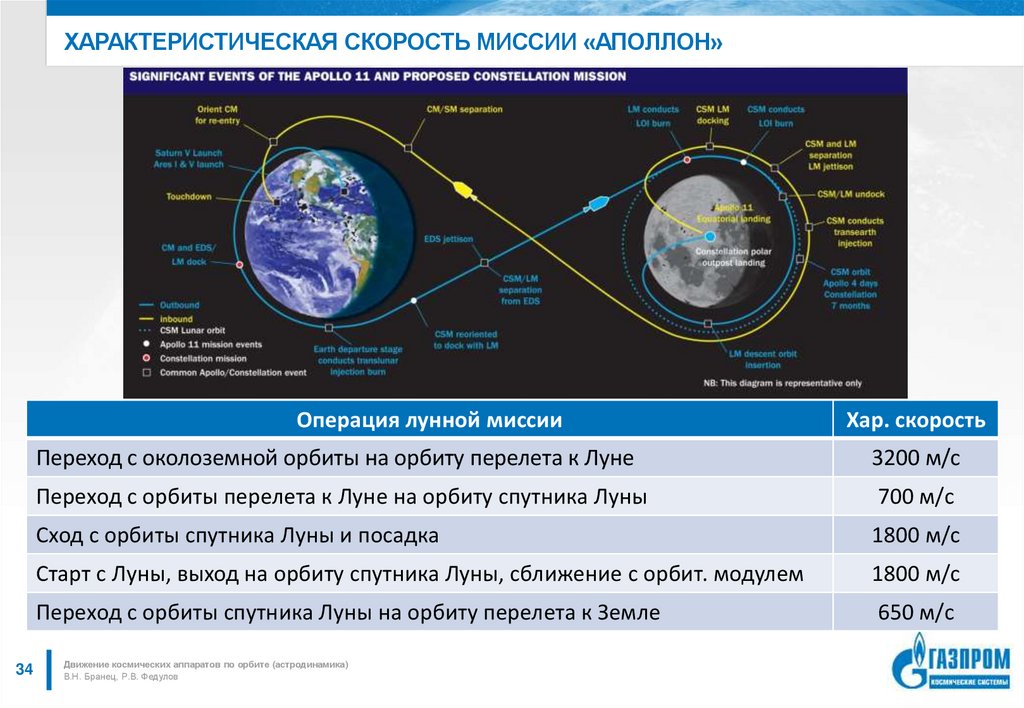
34. Характеристическая скорость миссии «аполлон»

ХАРАКТЕРИСТИЧЕСКАЯ СКОРОСТЬ МИССИИ «АПОЛЛОН»
Операция лунной миссии
34
Хар. скорость
Переход с околоземной орбиты на орбиту перелета к Луне
3200 м/с
Переход с орбиты перелета к Луне на орбиту спутника Луны
700 м/с
Сход с орбиты спутника Луны и посадка
1800 м/с
Старт с Луны, выход на орбиту спутника Луны, сближение с орбит. модулем
1800 м/с
Переход с орбиты спутника Луны на орбиту перелета к Земле
650 м/с
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

35. Перерыв 10 минут

ПЕРЕРЫВ 10 МИНУТ
Траектория 3-й ступени ракеты «Сатурн-5» в 2002–2003 годах.
14 ноября 1969 года ракета вывела на орбиту корабль «Аполлон-12».
L1 – точка Лагранжа системы Солнце – Земля.
35
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Для просмотра анимации нажмите F5

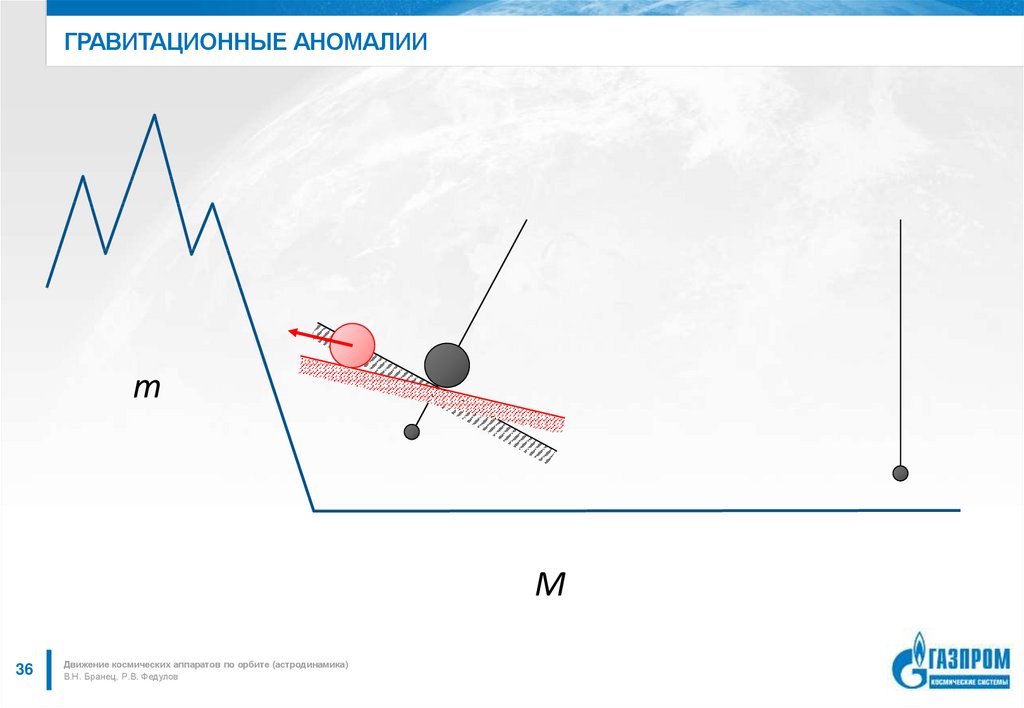
36. Гравитационные аномалии

ГРАВИТАЦИОННЫЕ АНОМАЛИИ
m
M
36
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

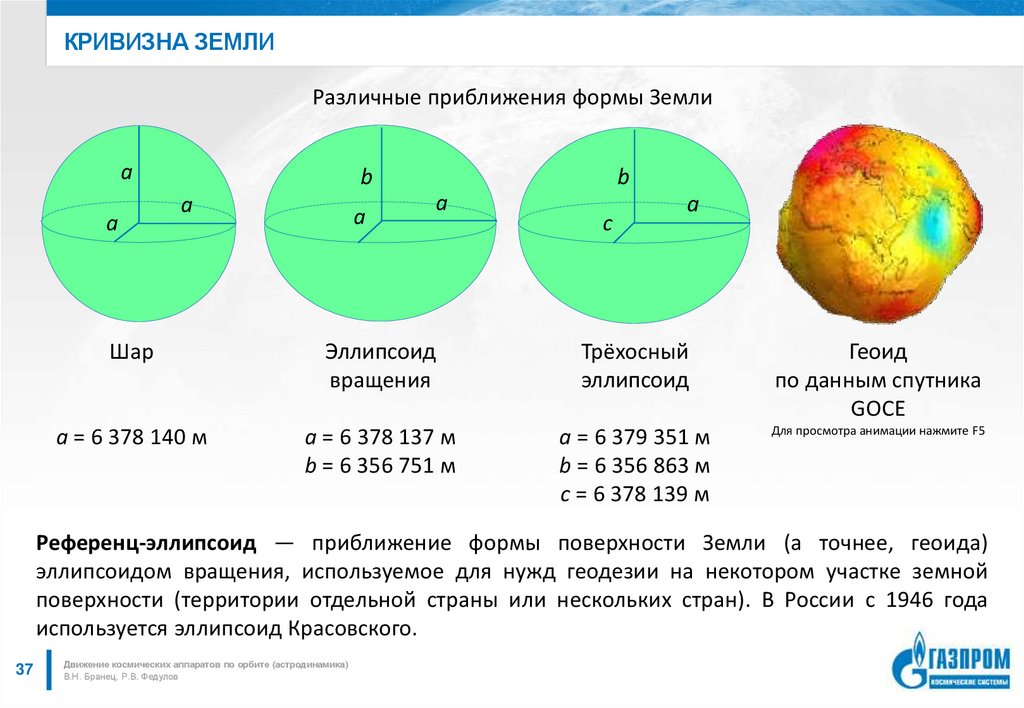
37. Кривизна земли

КРИВИЗНА ЗЕМЛИ
Различные приближения формы Земли
a
a
b
a
a
b
a
c
a
Шар
Эллипсоид
вращения
Трёхосный
эллипсоид
Геоид
по данным спутника
GOCE
a = 6 378 140 м
a = 6 378 137 м
b = 6 356 751 м
a = 6 379 351 м
b = 6 356 863 м
с = 6 378 139 м
Для просмотра анимации нажмите F5
Референц-эллипсоид — приближение формы поверхности Земли (а точнее, геоида)
эллипсоидом вращения, используемое для нужд геодезии на некотором участке земной
поверхности (территории отдельной страны или нескольких стран). В России с 1946 года
используется эллипсоид Красовского.
37
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

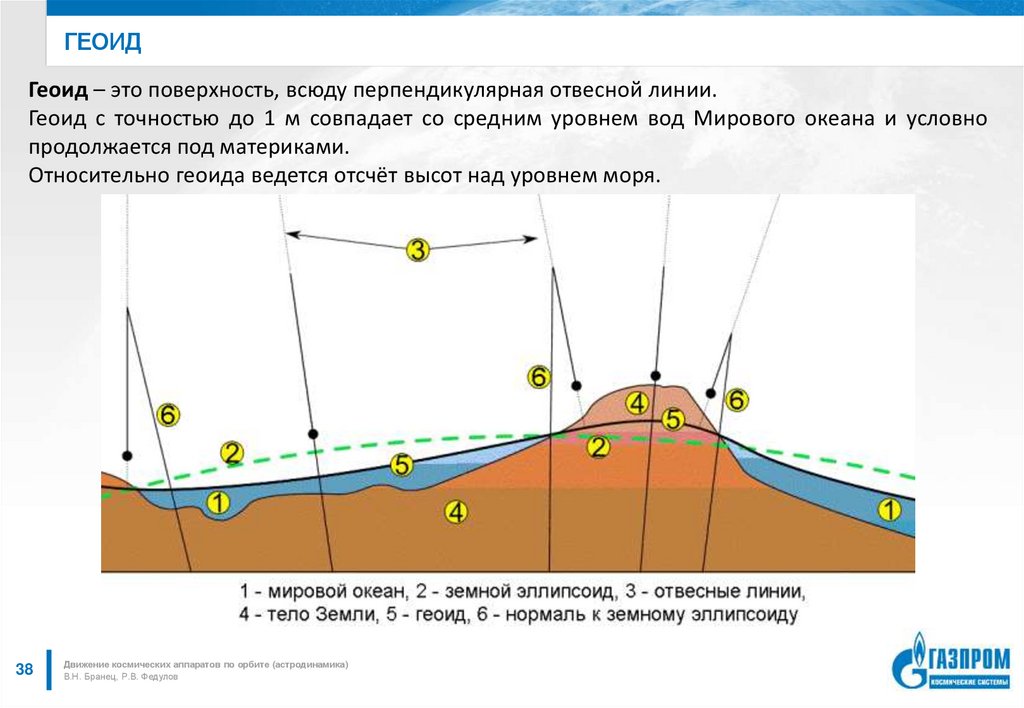
38. геоид

ГЕОИД
Геоид – это поверхность, всюду перпендикулярная отвесной линии.
Геоид с точностью до 1 м совпадает со средним уровнем вод Мирового океана и условно
продолжается под материками.
Относительно геоида ведется отсчёт высот над уровнем моря.
38
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

39. Земной Эллипсоид

ЗЕМНОЙ ЭЛЛИПСОИД
Сжатие:
a b
1
f
a
298, 26
Первый эксцентриситет:
b2 a 2 b2
1 2
f (2 f )
a
a2
2
Рассмотрим точки:
B r, z
C x ', y ', z ' r ', z '
O ' C местная вертикаль
OC геоцентрическая вертикаль
Сечение по меридиану
39
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Сечение по параллели
географическая широта
' геоцентрическая широта т. C
'' геоцентрическая широта т. B
OB
' OC

40. Связь между геоцентрической и географической широтой

СВЯЗЬ МЕЖДУ ГЕОЦЕНТРИЧЕСКОЙ И ГЕОГРАФИЧЕСКОЙ ШИРОТОЙ
tgφ' 1 f tgφ 1 2 tgφ
2
40
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

41. Координаты точки С через географические параметры

КООРДИНАТЫ ТОЧКИ С ЧЕРЕЗ ГЕОГРАФИЧЕСКИЕ ПАРАМЕТРЫ
Выражение для декартовых координат точки С=(R’,Z’) на поверхности Земли через
географическую широту φ и величину экваториального радиуса Земли а.
a cos φ
R ρ cos φ
1 f ( f 2)sin 2 φ
Z ρ sin φ a sin φ
(1 f )2
1 f ( f 2)sin 2 φ
можно ввести новый параметр N=O’C, с учетом которого
a cos φ
R
1 ε sin φ
2
2
(1 f )2
Z a sin φ
1 ε 2 sin 2 φ
N cos φ
( N ε 2 N ) sin φ
а сам параметр
N a 1 ε sin φ
41
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
2
2
1
2
a a cos φ b sin φ
2
2
2
2
2
1
2

42. Координаты точки B через географические параметры

КООРДИНАТЫ ТОЧКИ B ЧЕРЕЗ ГЕОГРАФИЧЕСКИЕ ПАРАМЕТРЫ
Выражение для декартовых координат точки B=(R,Z) на высоте h:
R ( N h) cos φ
Z ( N ε 2 N h)sin φ
Отсюда получаем связь между геоцентрической и географической широтой для объекта B на
высоте h:
Z N (1 ε 2 ) h
tgφ
tgφ
R
N h
Можно видеть, что при уменьшении высоты эта формула переходит в формулу для тангенса
геоцентрической широты точки на поверхности Земли.
42
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

43. Географические параметры через координаты объекта

ГЕОГРАФИЧЕСКИЕ ПАРАМЕТРЫ ЧЕРЕЗ КООРДИНАТЫ ОБЪЕКТА
Выражение для высоты h и географической широты φ из декартовых координат точки B=(R,Z):
h
R
N
cos φ
Z
Z
N h
N
2
tgφ
1
ε
R N (1 ε 2 ) h R
N h
1
Величина N также зависит от φ. Найти h и φ можно итерационным методом:
N1
Nk
43
A2
A cos 1 B sin 1
2
2
2
A2
A cos k B sin k
2
2
2
2
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
2
;
,
R
h1
N1;
cos 1
R
hk
Nk ;
cos k
Z
1 arctan 1 2
R
1
Z
Nk
k 1 arctan 1 2
N k hk
R
1

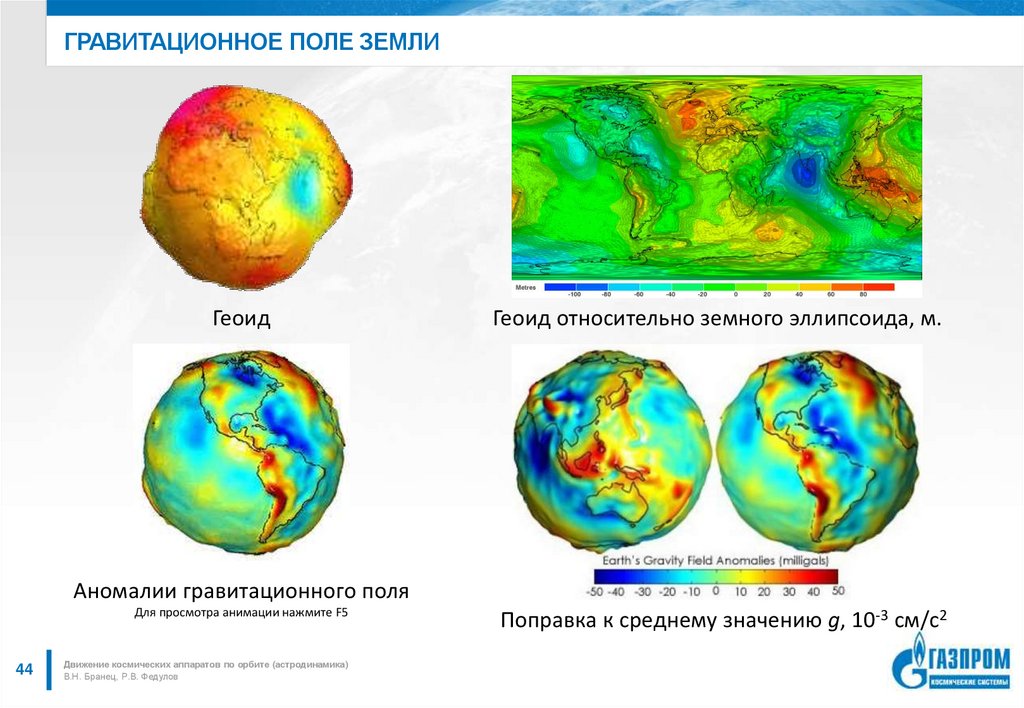
44. Гравитационное поле земли

ГРАВИТАЦИОННОЕ ПОЛЕ ЗЕМЛИ
Геоид
Геоид относительно земного эллипсоида, м.
Аномалии гравитационного поля
Для просмотра анимации нажмите F5
44
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
Поправка к среднему значению g, 10-3 см/с2

45. Спутник GOCE – исследователь гравитационного поля

СПУТНИК GOCE – ИССЛЕДОВАТЕЛЬ ГРАВИТАЦИОННОГО ПОЛЯ
Длина: 5,3 м
Диаметр: 2,3 м
Масса: 1100 кг
Высота орбиты: 250 км
Наклонение: 96°
Запуск: 17.03.2009
с космодрома
«Плесецк»
Окончание миссии:
11.11.2013 г.
45
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

46. Притяжение объёмного тела

ПРИТЯЖЕНИЕ ОБЪЁМНОГО ТЕЛА
Гравитационный потенциал Земли
z
U (r ) G
M
dM
ρ
γ
r
φ
λ
x
y
dM
r
G – гравитационная постоянная
M – масса Земли
Δr – расстояние от точки с массой dM до конца
вектора r, которое определяется формулой
r
rx ρ x ry ρ y rz ρ z
2
2
r ρ
2
2
r 2 ρ 2 2rρ cos γ
φ – угол между векторами ρ и r.
В общем случае интеграл можно вычислить только при помощи ряда.
Наибольшее распространение получило разложение геопотенциала в ряд по сферическим
функциям.
46
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

47. полиномы лежандра

ПОЛИНОМЫ ЛЕЖАНДРА
Рассмотрим дифференциальное уравнение второго порядка (уравнение Лежандра):
2
d
n n 1 u 0
1 z 2 dzu2 2 z du
dz
где z – комплексная переменная. Решения этого уравнения при целых n имеют вид
многочленов, называемых многочленами (полиномами) Лежандра. Полином Лежандра
степени n вычисляется по формуле:
n
2
n
2
1 d z 1
1 d cos θ 1
Pn z n
, а в полярных координатах Pn z n
n
2 n!
dz
2 n ! d cos θ n
n
где θ – косинус полярного угла, отсчитываемого от оси z. Несколько первых Pn(z):
P0 z 1,
P1 z z ,
1
3 z 2 1 ,
2
1
P3 z 5 z 3 3 z .
2
P2 z
47
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов
n

48. Присоединенные функции лежандра

ПРИСОЕДИНЕННЫЕ ФУНКЦИИ ЛЕЖАНДРА
Рассмотрим дифференциальное уравнение второго порядка
d 2u
du
m2
1 z dz 2 2z dz n n 1 1 z 2 u 0
2
которое при m = 0 переходит в уравнение Лежандра. Одним из решений данного уравнения
является присоединённая функция Лежандра:
Pn ,m z 1 z
2
m
2
d m Pn z
dz m
где Pn(z) – полином Лежандра. Присоединённые функции Лежандра являются составными
элементами сферических функций. Запишем несколько первых присоединённых функций
Лежандра Pn,m(z):
P01 0,
P11 1 z
1
2 2
,
P22 3 1 z 2 ,
1
3
2
2 2
P31 1 5 z 1 z .
2
48
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

49. Сферические функции

СФЕРИЧЕСКИЕ ФУНКЦИИ
Сферическая функция порядка n определяется формулой:
n
Yn θ,ψ Pn ,m cos θ An ,m cos mψ+Bn ,m sin mψ
m 0
где Pn,m(cosθ) – присоединённая функция Лежандра, An,m и Bn,m – произвольные постоянные.
Область определения – сфера, аргумент записывается в сферических координатах через
полярную широту θ, долготу ψ и иногда радиус r:
x r sin cos
y r sin sin
z r cos
49
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

50. Разложение потенциала в ряд по сферическим функциям

РАЗЛОЖЕНИЕ ПОТЕНЦИАЛА В РЯД ПО СФЕРИЧЕСКИМ ФУНКЦИЯМ
Стандартная форма записи геопотенциала, принятая Международным астрономическим
союзом:
n
n
a n
a
U 1 J n Pn ,0 sin Cn ,m cos m Sn ,m sin m Pn ,m sin
r
m 1 r
n 2 r
a – экваториальный радиус Земли;
Jn – коэффициенты зональных гармоник;
Cn,m и Sn,m – коэффициенты секториальных гармоник при n=m и тессеральных – при n≠m;
Pn,m(sinφ) – присоединённые функции Лежандра.
Чем больше учитывается гармоник, тем точнее геопотенциал, тем больше точность модели
орбитального движения и тем меньше ошибка прогноза орбиты.
50
КА
Порядок модели
гравитационного поля
Ошибка прогноза орбиты
на виток, м.
Ресурс-ДК
4
300
МКС
72
25
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

51. Смена знака гармоник геопотенциала

СМЕНА ЗНАКА ГАРМОНИК ГЕОПОТЕНЦИАЛА
Зональные гармоники
n=8
Секториальные гармоники
n = m = 10
Тессеральные гармоники
(τεσσερα – четыре)
n = 8, m = 10
Конкретные знаки в зонах, секторах и четырёхугольниках зависят от коэффициентов гармоник.
Коэффициенты Jn, Cn,m и Sn,m определяются путём геодезических и гравиметрических
измерений, с помощью наблюдений за траекториями ИСЗ, с помощью измерений,
проводимых научными спутниками (GOCE).
51
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

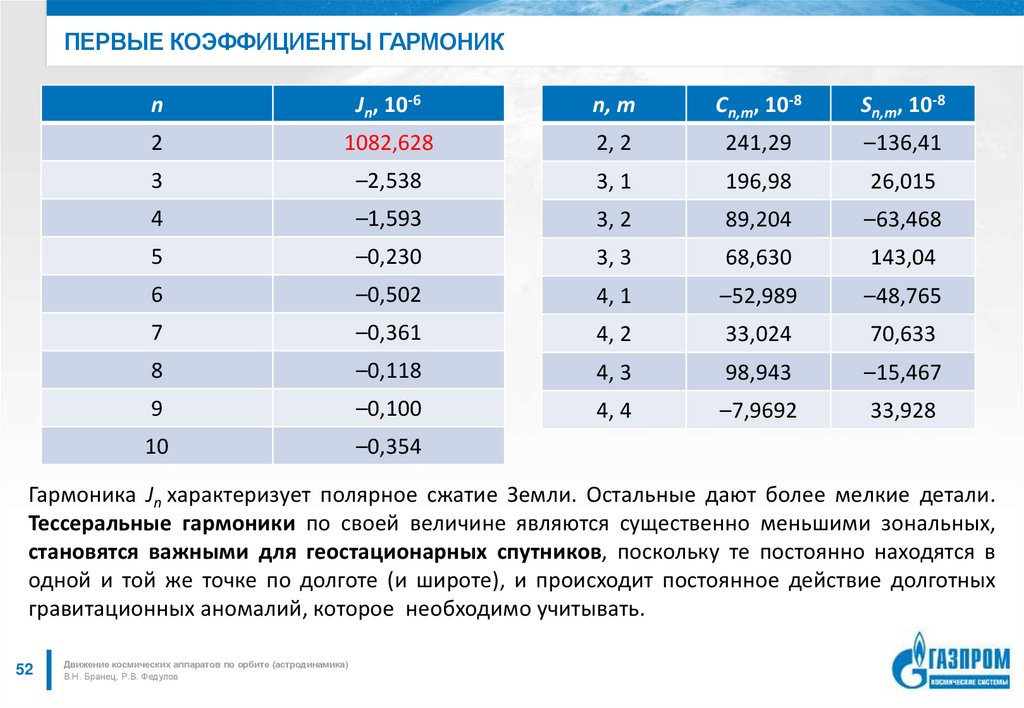
52. Первые коэффициенты гармоник

ПЕРВЫЕ КОЭФФИЦИЕНТЫ ГАРМОНИК
n
Jn, 10-6
n, m
Cn,m, 10-8
Sn,m, 10-8
2
1082,628
2, 2
241,29
–136,41
3
–2,538
3, 1
196,98
26,015
4
–1,593
3, 2
89,204
–63,468
5
–0,230
3, 3
68,630
143,04
6
–0,502
4, 1
–52,989
–48,765
7
–0,361
4, 2
33,024
70,633
8
–0,118
4, 3
98,943
–15,467
9
–0,100
4, 4
–7,9692
33,928
10
–0,354
Гармоника Jn характеризует полярное сжатие Земли. Остальные дают более мелкие детали.
Тессеральные гармоники по своей величине являются существенно меньшими зональных,
становятся важными для геостационарных спутников, поскольку те постоянно находятся в
одной и той же точке по долготе (и широте), и происходит постоянное действие долготных
гравитационных аномалий, которое необходимо учитывать.
52
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

53. Учет возмущений в вычислении орбит

УЧЕТ ВОЗМУЩЕНИЙ В ВЫЧИСЛЕНИИ ОРБИТ
Уравнение возмущённого движения :
d 2r
r
aвозм
2
3
dt
r
Какие возмущения оказывают влияние на движение аппарата по орбите?
53
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

54. Возмущающие ускорения для спутников GPS

ВОЗМУЩАЮЩИЕ УСКОРЕНИЯ ДЛЯ СПУТНИКОВ GPS
Возмущающий фактор
Ускорение, м/с2
Полярное сжатие Земли (J2)
5·10-5
Другие гармоники геопотенциала
3·10-7
Гравитационное влияние Луны
5·10-6
Гравитационное влияние Солнца
2·10-6
Гравитационное влияние планет
3·10-10
Тектонические приливы
2·10-9
Океанские приливы
5·10-10
Солнечное давление
1·10-7
Лобовое сопротивление атмосферы
4·10-10
Релятивистские эффекты
3·10-10
Источник:
Guochang Xu GPS Theory, Algorythms and Applications 2nd Edition – Springer, 2007
54
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

55. Оскулирующая орбита

ОСКУЛИРУЮЩАЯ ОРБИТА
Оскулирующая орбита (в заданный момент времени t0) – это кеплерова орбита, которую
аппарат (в соответствии с его фактическим положением и скоростью) имел бы при отсутствии
в дальнейшем каких-либо возмущений.
Для оскулирующей орбиты положение и скорость КА можно вычислять с помощью
соотношений задачи двух тел по интегралам движения.
На некотором интервале после t0 оскулирующая орбита хорошо описывает реальное
движение, однако точность такого приближения ухудшается со временем пропорционально
возмущению.
v t0
реальная орбита
r t0
оскулирующая орбита
55
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

56. Изменение орбитальных параметров

ИЗМЕНЕНИЕ ОРБИТАЛЬНЫХ ПАРАМЕТРОВ
Изменение большой полуоси:
da 2a 2
v aвозм
dt
Изменение модуля момента количества движения:
dc 1 2
r v aвозм r v r aвозм
dt c
Изменение эксцентриситета:
de
1
pa r 2 v aвозм r v r aвозм
dt ae
Изменения наклонения и долготы восходящего узла:
dΩ
c
sin
i
dt
sin Ω
0
cos Ω
di
c
sin Ω cos i cos Ω cos i sin i r aвозм
dt
sin Ω sin i cos Ω sin i cos i
dc
dt
56
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

57. Изменение орбитальных аномалий

ИЗМЕНЕНИЕ ОРБИТАЛЬНЫХ АНОМАЛИЙ
Изменение истинной аномалии:
dθ c dη
dt r 2 dt
Изменение эксцентрической аномалии:
dE na dβ
dt
r dt
Изменение средней аномалии:
dM
dγ
n
dt
dt
где
η t0 t θ t0 t θ t0
β t0 t E t0 t E t0
γ t0 t M t0 t M t0
n – среднее движение.
57
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

58. Влияние полярного сжатия на смещение плоскости орбиты

ВЛИЯНИЕ ПОЛЯРНОГО СЖАТИЯ НА СМЕЩЕНИЕ ПЛОСКОСТИ ОРБИТЫ
Зональная гармоника J2 приводит к постоянному изменению долготы восходящего угла
орбиты со скоростью
2
3 a
Ω = J 2 n cos i
2 p
где n – среднее движение.
Наклонение орбиты
Направление вращения плоскости орбиты
i < 90°
противоположно направлению движению спутника
i > 90°
по направлению движения спутника
Выбором параметров орбиты скорость движения восходящего узла можно сделать равной
0,9856 °/сутки, т.е. один полный оборот за год. Такая орбита называется солнечносинхронной, поскольку ориентация плоскости относительно Солнца остаётся неизменной.
58
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

59. Влияние полярного сжатия на смещение перигея

ВЛИЯНИЕ ПОЛЯРНОГО СЖАТИЯ НА СМЕЩЕНИЕ ПЕРИГЕЯ
Зональная гармоника J2 приводит к изменению аргумента перигея со скоростью,
2
3 A
J 2 n 4 5sin 2 i
4 p
Из этого уравнения следует, что линия апсид неподвижна при
4
5
i 63, 453
sin 2 i
59
Наклонение орбиты
Направление вращения линии апсид
i < 63,435°
в направлении орбитального движения
i > 63,435°
против орбитального движения
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

60. литература

ЛИТЕРАТУРА
1. Бранец В.Н., Севастьянов Н.Н., Федулов Р.В. Лекции по теории систем ориентации,
управления движением и навигации. – Томск: ТГУ, 2013.
2. Раушенбах Б.В., Овчинников М.Ю. Лекции по динамике космического полета. –
Москва: МФТИ, 1997.
3. Бебенин Г.Г., Сребушевский Б.С., Соколов Г.А. Системы управления полетом
космических аппаратов. – Москва: Машиностроение, 1978.
4. Лысенко Л.Н. Наведение и навигация баллистических ракет. – Москва: МГТУ им.
Баумана, 2007.
5. Аксенов Е.П. Теория движения искусственных спутников земли. – Москва: Наука, 1977.
6. Бордовицына Т.В., Авдюшев В.А. Теория движения искусственных спутников земли. –
Томск: ТГУ, 2007.
7. Бэттин Р.Х. Наведение в космосе. – Москва: Машиностроение, 1966.
8. Wertz J.R. Spacecraft Attitude Determination and Control. – Kluwer Academic Publishers,
2002.
9. Griffin M.D., French J.R. Space Vehicle Design. – AIAA Education Series, 2004.
10. Guochang Xu GPS Theory, Algorythms and Applications 2nd Edition – Springer, 2007.
60
Движение космических аппаратов по орбите (астродинамика)
В.Н. Бранец, Р.В. Федулов

61. Спасибо за внимание

СПАСИБО ЗА ВНИМАНИЕ