Similar presentations:
Гетероскедастичность случайной составляющей
1.
Модель множественной регрессии всегда включает случайную составляющуюB c aYD bP
Наличие случайной составляющей связано в тем, что помимо факторов,
вошедших в модель на зависимую переменную могут влиять и другие
неучтенные факторы.
Метод наименьших квадратов является наилучшим только если случайная
составляющая обладает двумя свойствами
1) случайная составляющая является гомоскедастичной
(имеет постоянную дисперсию)
2) в случайной составляющей отсутствует автокорреляция
1
2. Гетероскедастичность случайной составляющей
Пусть нарушено первое условиеD const
Тогда говорят, что имеет место
гетероскедастичность, т.е. ошибки регрессии
имеют непостоянные дисперсии
В этом случае МНК не является лучшим методом.
2
3.
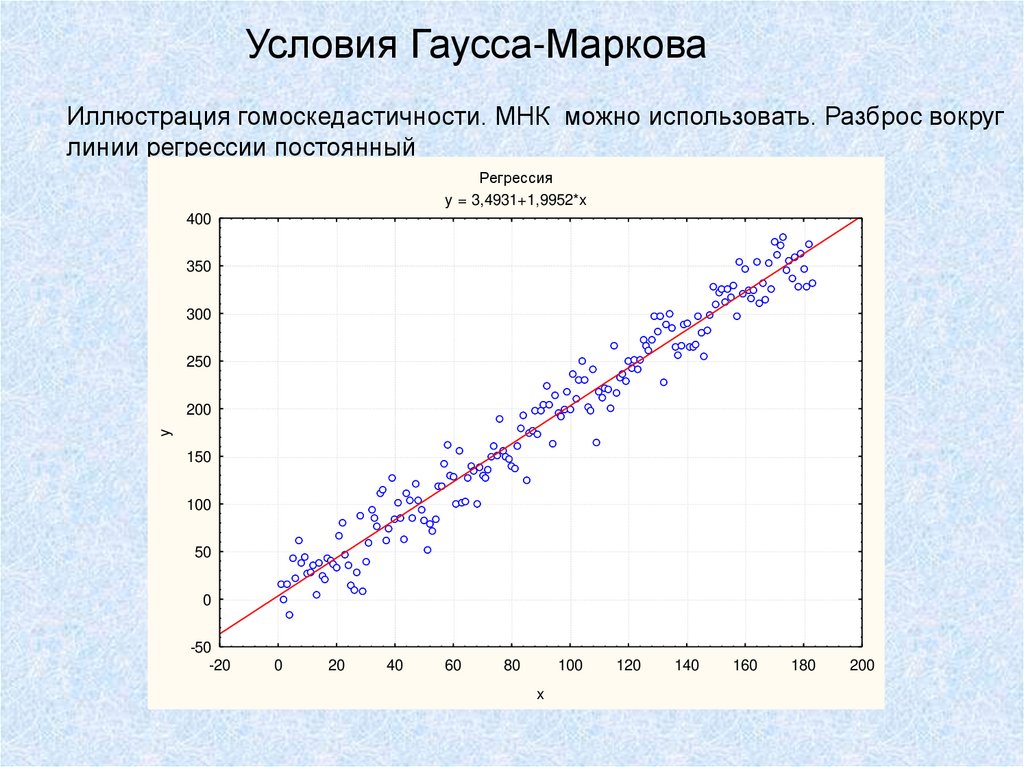
Условия Гаусса-МарковаИллюстрация гомоскедастичности. МНК можно использовать. Разброс вокруг
линии регрессии постоянный
Регрессия
y = 3,4931+1,9952*x
400
350
300
250
y
200
150
100
50
0
-50
-20
0
20
40
60
80
100
x
120
140
160
180
200
4.
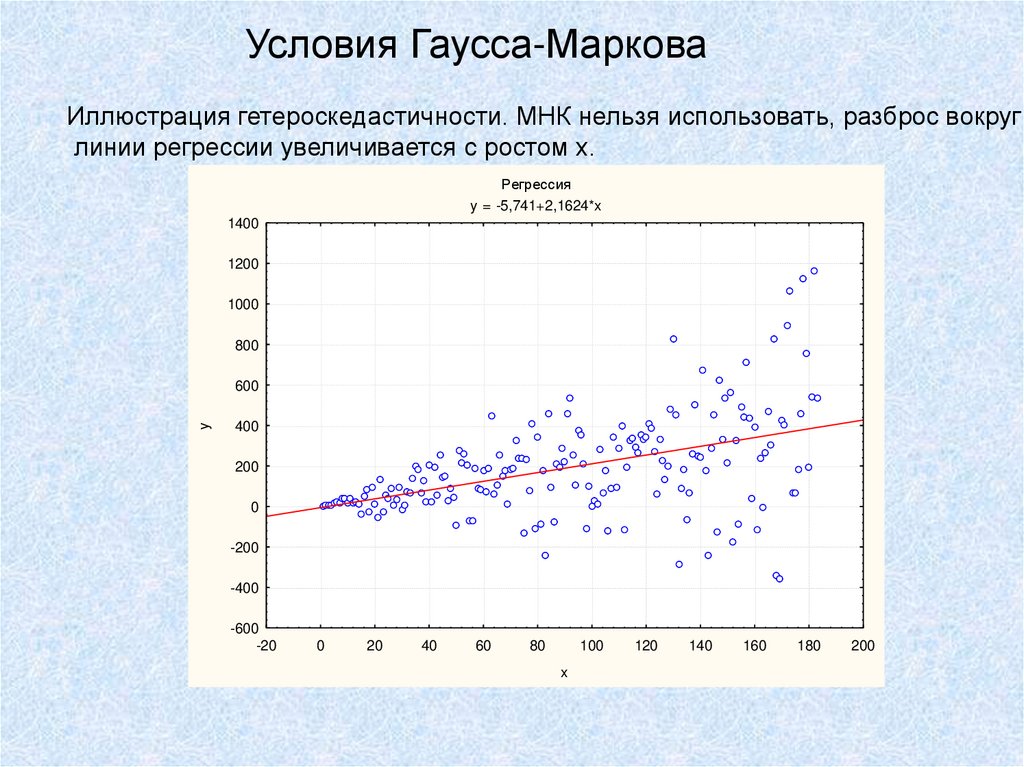
Условия Гаусса-МарковаИллюстрация гетероскедастичности. МНК нельзя использовать, разброс вокруг
линии регрессии увеличивается с ростом х.
Регрессия
y = -5,741+2,1624*x
1400
1200
1000
800
y
600
400
200
0
-200
-400
-600
-20
0
20
40
60
80
100
x
120
140
160
180
200
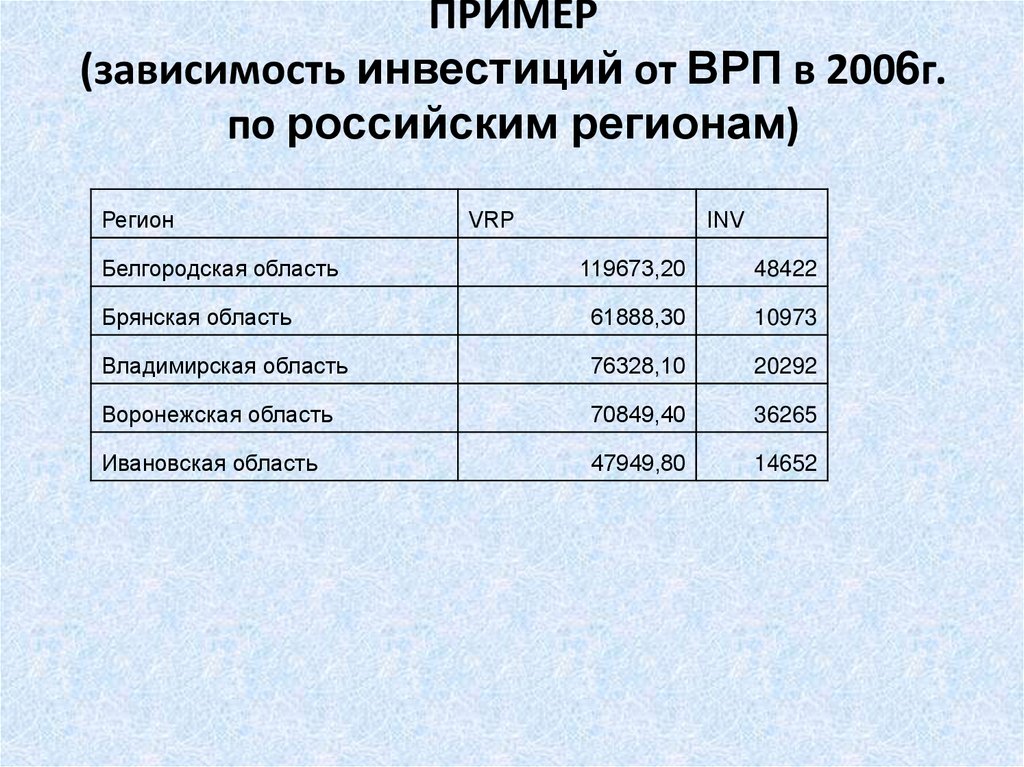
5. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
РегионБелгородская область
VRP
INV
119673,20
48422
Брянская область
61888,30
10973
Владимирская область
76328,10
20292
Воронежская область
70849,40
36265
Ивановская область
47949,80
14652
6. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
Коэффициенты
Станда
ртная
ошибка
Yпересечение
5164,439
11352,89 0,454901 0,650428
VRP
0,345983 0,070519 4,906268
INV 0,346 VRP 5164
tстатис
тика
PЗначени
е
4,88E-06
7. ПРИМЕР (зависимость инвестиций от ВРП в 2006г. по российским регионам)
600000500000
INV
400000
300000
y = 0,346x + 5164,4
200000
100000
0
0,00
200000,0 400000,0 600000,0 800000,0 1000000,
0
0
0
0
00
VRP
Разброс вокруг линии регрессии увеличивается с ростом ВРП. Есть
непостоянство дисперсии (гетероскедастичность)
8. График остатков в зависимости от ВРП также позволяет увидеть гетероскедастичность, чем больше ВРП, тем больше по модулю остатки
eОстатки
500000
400000
300000
200000
100000
0
-1000000,00
-200000
-300000
Остатки
200000 400000 600000 800000 100000
,00
,00
,00
,00
0,00
VRP
8
9. ПОСЛЕДСТВИЯ ГЕТЕРОСКЕДАСТИЧНОСТИ
1. Обычная МНК оценка становится не самойточной (есть более точные оценки).
2. Проверка значимости коэффициентов
становится некорректной
9
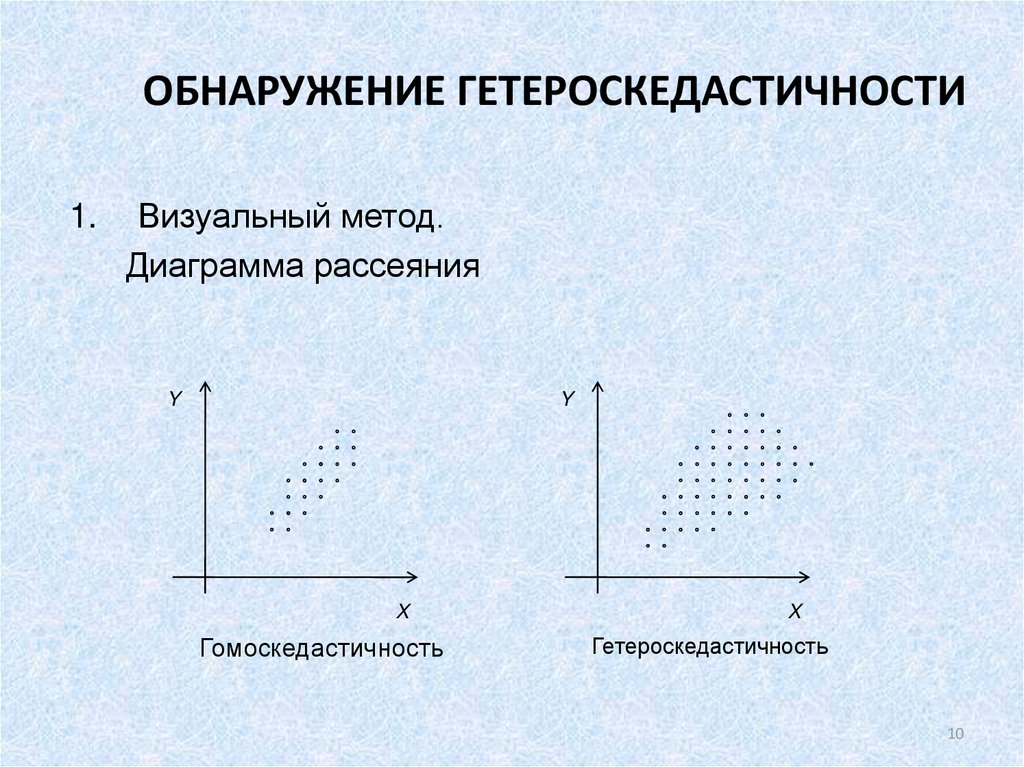
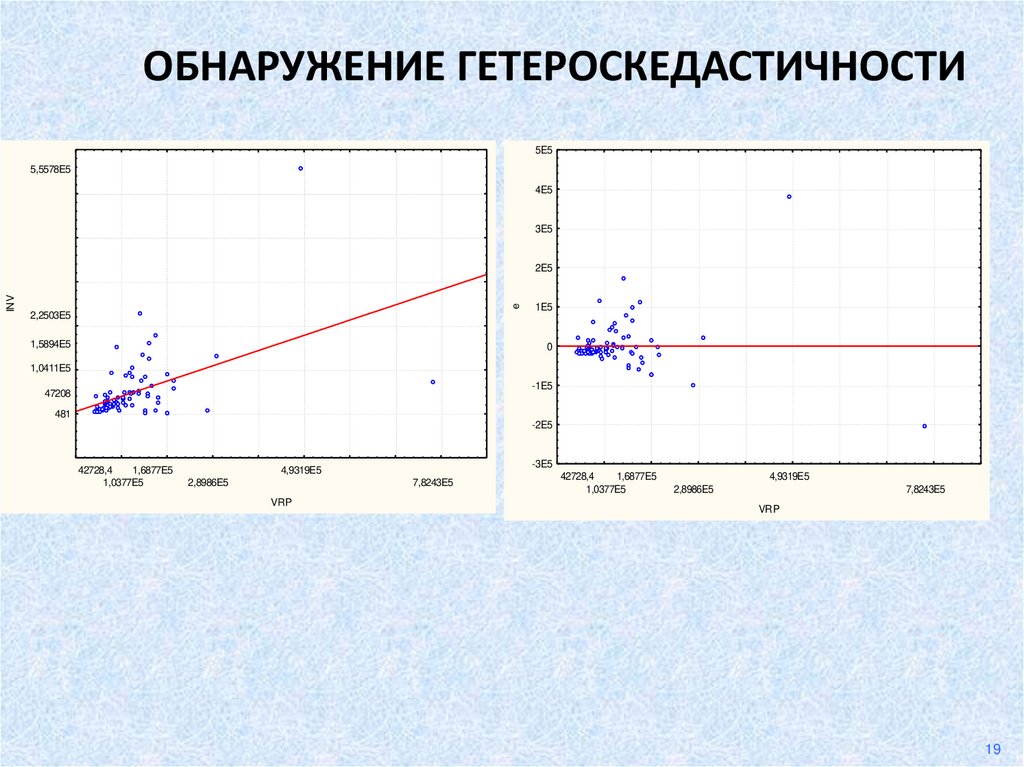
10. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
1.Визуальный метод.
Диаграмма рассеяния
Y
Y
X
Гомоскедастичность
X
Гетероскедастичность
10
11. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
1.Визуальный метод.
Графики остатков после построения оценок по
методу МНК
e
e
X или Y
Гомоскедастичность
X или Y
Гетероскедастичность
11
12.
ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ5E5
5,5578E5
4E5
3E5
e
INV
2E5
2,2503E5
1,5894E5
1E5
0
1,0411E5
-1E5
47208
481
-2E5
42728,4
1,6877E5
1,0377E5
-3E5
4,9319E5
2,8986E5
7,8243E5
VRP
42728,4
1,6877E5
1,0377E5
4,9319E5
2,8986E5
7,8243E5
VRP
19
13. ОБНАРУЖЕНИЕ ГЕТЕРОСКЕДАСТИЧНОСТИ
Кроме визуального метода используются более точные методыТесты:
1. Тест ранговой корреляции Спирмена.
2. Тест Глейзера.
3. Тест Голдфелда-Квандта.
4. Тест Уайта.
В специализированных эконометрических пакетах эти тесты есть
13
14. Устранение ГЕТЕРОСКЕДАСТИЧНОСТИ
1) Использовать обобщенный методнаименьших квадратов
В этом методе предполагается, что
стандартное отклонение остатков
пропорционально одной из объясняющих
переменных
Например,
INV aVRP b k VRP
14
15. Устранение гетероскедастичности пример
INV aVRP bk VRP
Делим уравнение на эту объясняющую переменную (в примере на ВРП )
INV
1
a b
VRP
VRP VRP
Тогда
1
1
2
2
2
D
D
k
VRP
k
const
2
2
VRP VRP
VRP
16. Устранение гетероскедастичности пример
INV1
a b
VRP
VRP VRP
Создаем новые переменные
INV
1
,
VRP VRP
Регион
Белгородская область
VRP
INV
INV/VRP
1/VRP
119673,20
48422
0,40
8,36E-06
Брянская область
61888,30
10973
0,18
1,62E-05
Владимирская область
76328,10
20292
0,27
1,31E-05
Воронежская область
70849,40
36265
0,51
1,41E-05
Ивановская область
47949,80
14652
0,31
2,09E-05
Калужская область
83817,40
16268
0,19
1,19E-05
17. Устранение гетероскедастичности пример
INV1
a b
VRP
VRP VRP
Коэффициент
ы
Стандартная
ошибка
t-статистика
Y-пересечение
0,491025
0,0864
5,683151
2,13E-07
1/VRP
-11337,2
7354,391
-1,54156
0,127178
INV
1
0,5 11,337
,
VRP
VRP
INV 0,5 VRP 11,337
P-Значение
18. Устранение гетероскедастичности пример
INV1
a b
VRP
VRP VRP
Остатки
1,5
1
0,5
e
Остатки
0
-0,5 0
5E-06
0,00001 1,5E-05 0,00002 2,5E-05
-1
1/VRP
Визуально гетероскедастичность отсутствует
19. 2) Изменить функциональную форму модели
Scatterplot (Spreadsheet1 10v*119c)y = -2554,0902+132,073*x
35000
30000
25000
y
20000
15000
10000
5000
0
-5000
-20
0
20
40
60
80
100
120
140
x
С ростом х растет разброс вокруг линии регрессии. Есть гетероскедастичность
20. 2) Изменить функциональную форму модели
Прологарифмируем данные и построим модель в логарифмахScatterplot (Spreadsheet1 10v*119c)
12
10
8
ln(y)
6
4
2
0
-2
-1
0
1
2
3
4
5
ln(x)
Разброс постоянный вокруг линии регрессии. Нет гетероскедастичности.
Таким образом, нужно строить степенную модель вместо линейной















 mathematics
mathematics








