Similar presentations:
Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками
1. Линейные регрессионные модели с гетероскедастичными и автокоррелированными остатками
1.2.
3.
4.
Предпосылки метода наименьших квадратов
Гетероскедостичность, выявление и устранение
Автокорреляция, выявление и устранение
Мультиколлениарность, выявление и устранение
5. Проблемы спецификации модели
2. Автокорреляция, выявление и устранение
3.
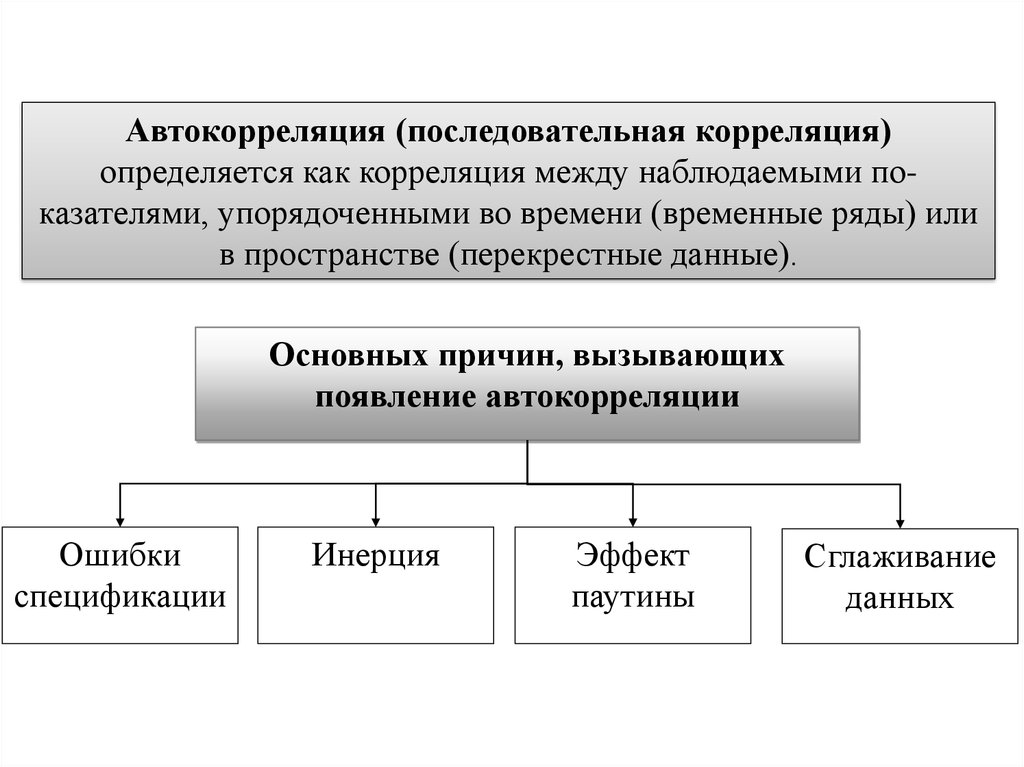
Автокорреляция (последовательная корреляция)определяется как корреляция между наблюдаемыми показателями, упорядоченными во времени (временные ряды) или
в пространстве (перекрестные данные).
Основных причин, вызывающих
появление автокорреляции
Ошибки
спецификации
Инерция
Эффект
паутины
Сглаживание
данных
4. Последствия автокорреляции:
1. Оценки параметров, оставаясь линейными инесмещенными, перестают быть эффективными
2. Дисперсии оценок являются смещенными
3. Оценка дисперсии регрессии 2 является смещенной
оценкой истинного значения генеральной дисперсии, во
многих случаях занижая его
4. Выводы по t- и F-статистикам, определяющим
значимость коэффициентов регрессии и коэффициента
детерминации, возможно, будут неверными случаях
занижая его
5. Методы обнаружения автокорреляции:
1.2.
3.
4.
5.
6.
графический анализ остатков
метод рядов
критерий Дарбина-Уотсона
тест серий Бреуша-Годфри
Q-тест Льюинга-Бокса
тест Льюинга-Бокса
6.
Графический анализа остатков0,04
εi2εi2
εi2
0,03
0,02
отсутствие автокорреляции
отклонения
0,01
0,00
t t
-0,01
t
Возрастающая
Случайные
остатки
тенденция в остатках
-0,02
Циклические колебания в остатках
-0,03
наличие автокорреляции
-0,04
-0,05
-0,06
0
2
4
6
8
10
t
12
14
16
18
95% confidence
20
7.
Метод рядовПоследовательно определяются знаки отклонений t
(------) (++++++++) (---) (++++) (-)
6 «-», 8 «+», 3 «-», 4 «+», 1 «-» при T=22
Если при достаточно большом количестве наблюдений
(T1>10, T2>10) количество рядов k лежит в пределах
то гипотеза об отсутствии автокорреляции не отклоняется
В нашем случае T1=12, T2=10, k=5, M(k)=11,91, D(k)=5,148
6,75<5<17,06
8.
Критерий Дарбина-Уотсона1 этап: Строят уравнение регрессии и находят отклонения t
2 этап: Рассчитывают величину:
3 этап: Проверяют выполняемость условий:
DW<d1 – в ряду автокорреляция есть;
DW>d2 – в ряду автокорреляции нет;
d1<DW<d2 – гипотеза о независимости выполняется условно
и необходимо дальнейшее исследование границ критерия
Механизм проверки гипотезы о наличии автокорреляции
остатков
Есть положительная
автокорреляция
остатков. Н0
отклоняется с
вероятностью Р=(1 ) принимается Н1
0
d1
Зона
неопредел
енности
Нет оснований
Зона
отклонять Н0
неопределе
(автокорреляция
нности
остатков отсутствует)
d2
2
4-d1
Есть отрицательная
автокорреляция
остатков. Н0
отклоняется с
вероятностью Р=(1 ) принимается Н1
4-d2
4
9.
Тест серий Бреуша-Годфри1 шаг: вычисляем регрессионное уравнение и находим
отклонения;
2 шаг: строим уравнение:
3 шаг: на основе t-критерия Стьюдента проверяют
статистическую значимость параметра .
Если tфакт > tтабл (параметр статистически значим), то в
анализируемом ряду наблюдается автокорреляции.
10.
Авторегрессионная схема первого порядкаСтроят парное линейное уравнение регрессии:
Наблюдению с индексом t соответствует выражение:
Наблюдению с индексом t-1 соответствует выражение:
Отклонения подвержены воздействию авторегрессии первого порядка:
Последовательно заменяя
получим:
11.
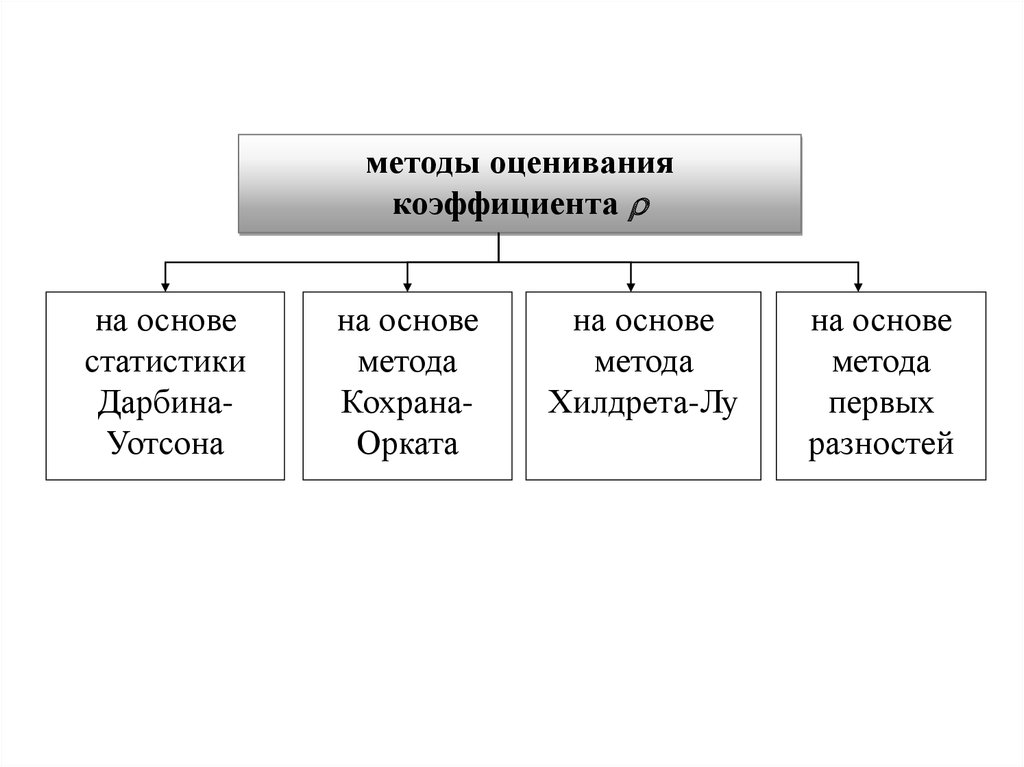
методы оцениваниякоэффициента
на основе
статистики
ДарбинаУотсона
на основе
метода
КохранаОрката
на основе
метода
Хилдрета-Лу
на основе
метода
первых
разностей
12.
Метод Кохрана-Орката1 этап: Оценивается по МНК регрессия и для нее определяются
оценки отклонений t;
2 этап: Оценивается регрессионная зависимость:
3 этап: На основе данной оценки строится уравнение:
4 этап: Значения
в уравнение регрессии:
и
подставляются
Затем вновь вычисляются оценки t отклонений и
возвращаются ко второму этапу.
13.
Определение на основестатистики
Дарбина-Уотсона
Определение на основе
метода
Хилдрета-Лу
оценивается для каждого возможного значения из
отрезка [-1,1]
14.
Метод первых разностейполагают = 1
Последовательно заменяя












 mathematics
mathematics








