Similar presentations:
Линейные регрессионные модели с гетероскедастичными остатками
1. ЛИНЕЙНЫЕ РЕГРЕССИОННЫЕ МОДЕЛИ С ГЕТЕРОСКЕДАСТИЧНЫМИ ОСТАТКАМИ
2.
Несмещенностьген
M (b j ) b j
Эффективность
ген 2
M (b j b j )
2
b
j
2
min b
j
Состоятельность
ген
b j b j
n
3.
Задачи регрессионного анализа:• Построение модели
• Исследование случайных отклонений
i yi yˆi
4.
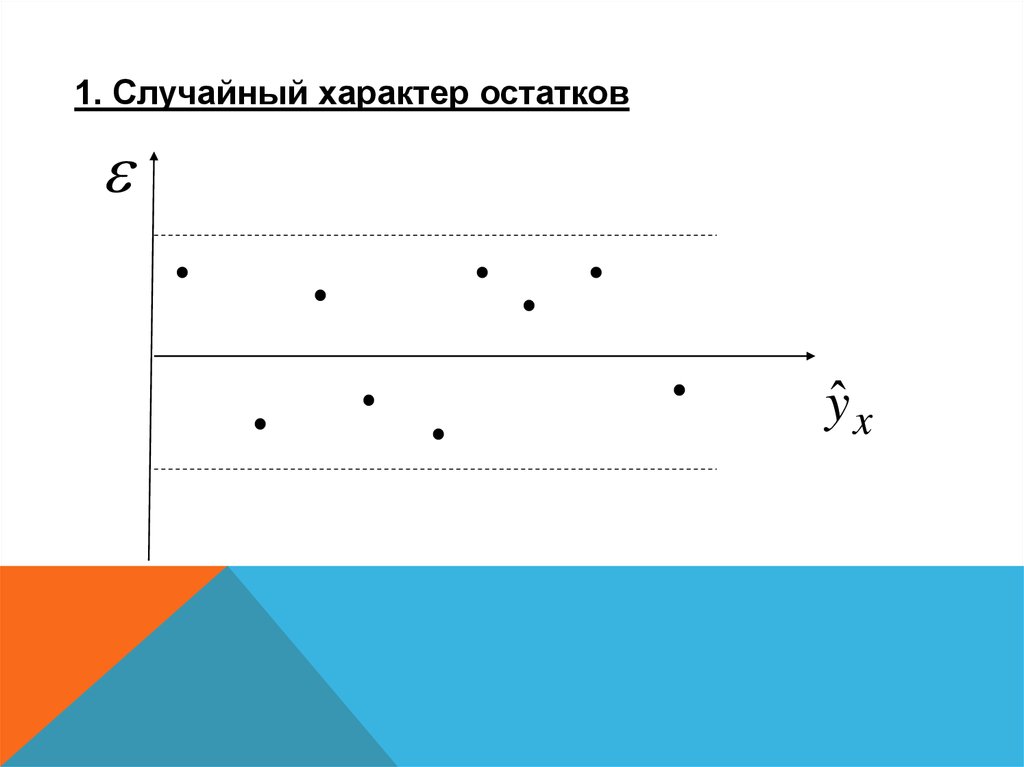
Пять предпосылок МНК:1. Случайный характер остатков
2. Нулевая средняя величина остатков, не зависящая от
xi
3. Гомоскедастичность
4. Отсутствие автокорреляции остатков
5. Остатки подчиняются нормальному распределению
5.
1. Случайный характер остатковyˆ x
6.
2. Нулевая средняя величина остатков( y yˆ x ) 0
2. Независимость величины остатков от величины
фактора x
xj
7.
8.
нарушение третьей предпосылки МНК.неправильная спецификация модели.
наличие систематической погрешности модели.
9.
3. Гомоскедастичность дисперсии остатков1. Оценки коэффициентов - несмещенные и
линейные.
2. Оценки коэффициентов не эффективные
3. Дисперсии оценок будут рассчитываться со
смещением.
4. Ненадежные интервальные оценки
коэффициентов.
10.
4. Отсутствие автокорреляции остатковКоэффициент корреляции
r i i 1
r i i 1 0
cov( i , i 1 )
i i 1
Остатки
автокоррелированы
11.
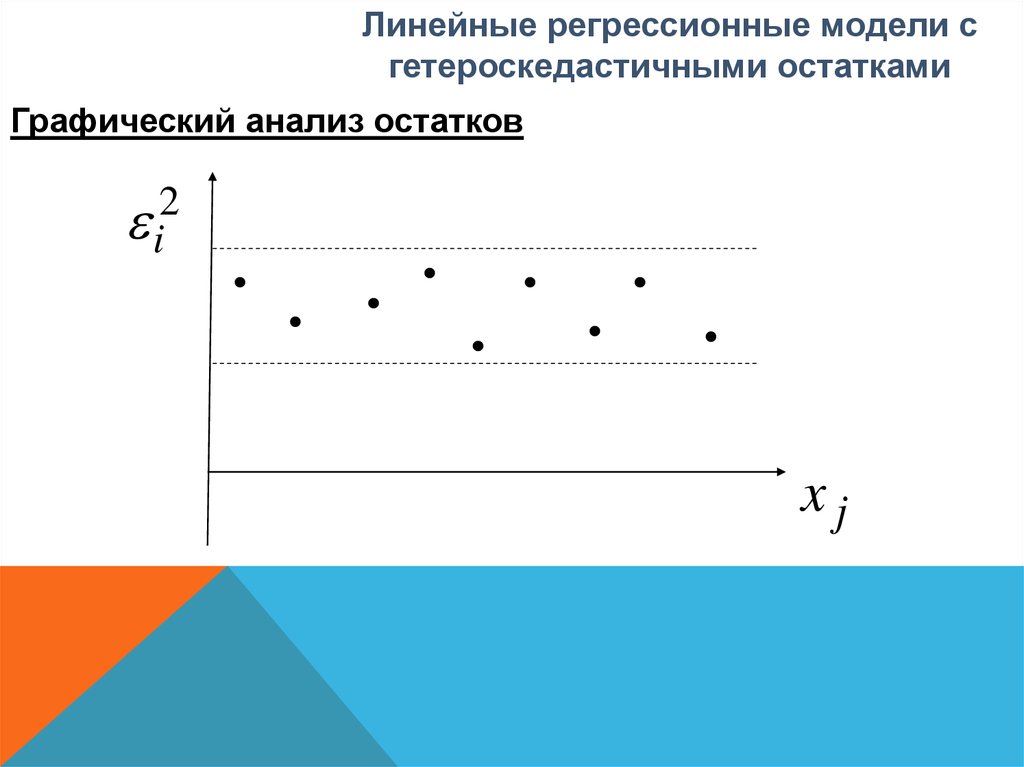
Линейные регрессионные модели сгетероскедастичными остатками
Графический анализ остатков
2
i
xj
12.
Линейные регрессионные модели сгетероскедастичными остатками
Тест Гольдфельда-Кванта
i ( xi ) xi
x
2
i
2
2
i
13.
Линейные регрессионные модели сгетероскедастичными остатками
Тест Гольдфельда-Кванта
1. Все наблюдения упорядочиваются по доминирующему
фактору
2. Упорядоченная совокупность делится на три группы:
k , (n 2 k ), k
3. По первой и третьей группе оцениваются регрессии
14.
Тест Гольдфельда-Кванта4.
5.
Fфакт
H 0 : S1 S3
Fфакт
H1 : S1 S3
S3 /(k m 1) S 3
.
S 1/(k m 1) S1
S3
Fтабл
S1
df1 df 2 k m 1
Остатки
гетероскедастичны
15.
ТестыПарка,
Глэйзера,
Уайта
1. Парка
ln a b ln x ji vi
2
i
x ji i е значение j го фактора
vi случайный остаток
16.
ТестыПарка,
Глэйзера,
Уайта
1. Глэйзера
i a bx kji vi ,
k какое либо число, например,
k 1; 0,5 ;0,5 ;1
2. Уайта
a b11 x1i b x b21 x2i b x c12 x1i x2i vi
2
i
2
12 1i
2
22 2i
17.
Тест ранговой корреляции Спирмена1. Ранжируются значения модулей остатков и
значения выбранного фактора
2. Вычисляется коэффициент Спирмена
rx ,
6 d
1
2
n (n 1)
2
i
d - разность между рангами i-го остатка и i–го фактора
18.
Тест ранговой корреляции Спирмена3.
H 0 : rx , 0
H1 rx , 0
tфакт tтабл
df n 2
t
rx , n 2
1 r
2
x ,
остатки
гетероскедастичны
19.
Обобщенный метод наименьших квадратовi
yi a b xi i
yi
i
i
D
i
a
i
b
xi
i
i
i
2
1 2 ( i ) i 1
2
2
i
i
20.
Обобщенный метод наименьших квадратов2
2
i
i
K
yi
xi
i
a
b
Ki
Ki
Ki
Ki
yi a bxi i
i ( i ) Ki
2
i
Ki
2
2
2
1
1
2
( i ) 2 K i 2 const
Ki
Ki
21.
Обобщенный метод наименьших квадратовn
1
2
S a, b yi a bxi
i 1 K i
1
K x y
b
1 2
K x
x y
b
x
2
22.
Обобщенный метод наименьших квадратовyi a b1 x1i b2 x2i i
K
2
i
i K
2
2
2
i
x1i
x 2i i
yi
a
b1
b2
Ki Ki
Ki
Ki Ki
23.
Обобщенный метод наименьших квадратовy a b1 x1 b2 x2 ... bm xm
K i x1i
i x
2
2
2
1i
x2i
xmi i
yi
1
a b1 b2
... bm
x1i
x1i
x1i
x1i x1i
24.
4. Автокорреляцияr i i 1
cov( i , i 1 )
i i 1
( i i 1 )
DW
2
i
2
DW 2 (1 r i i 1 )
25.
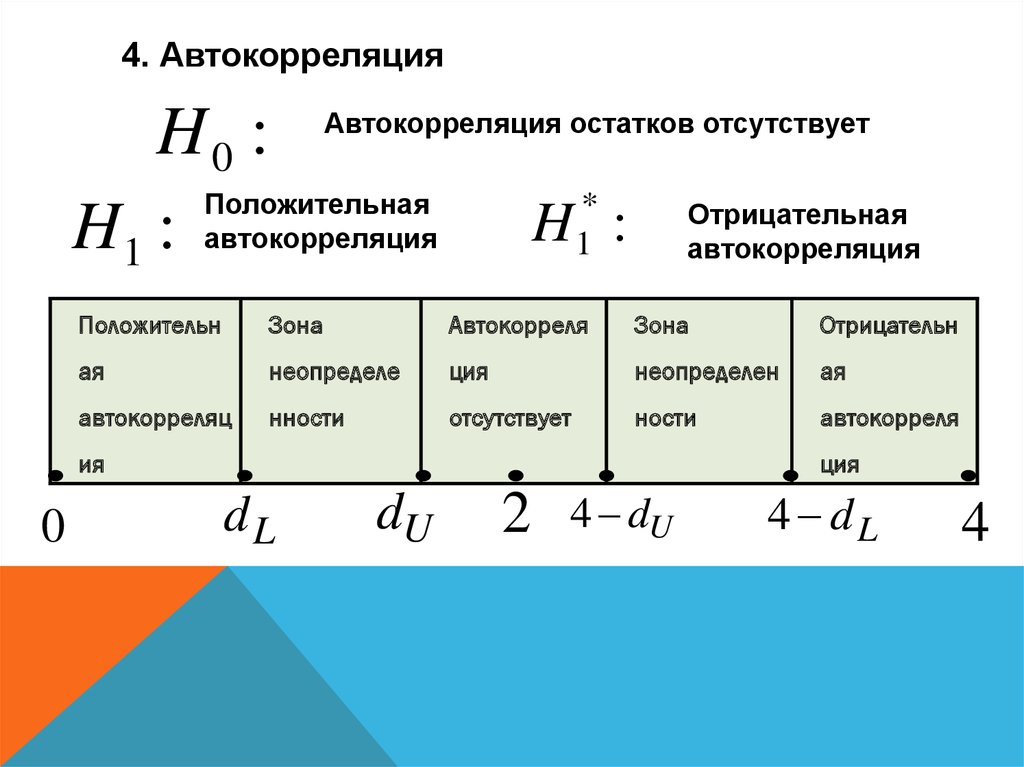
4. АвтокорреляцияH0 :
Положительная
H 1 : автокорреляция
Автокорреляция остатков отсутствует
*
1
Отрицательная
автокорреляция
H :
Положительн
Зона
Автокорреля
Зона
Отрицательн
ая
неопределе
ция
неопределен
ая
автокорреляц
нности
отсутствует
ности
автокорреля
ия
0
ция
dL
dU
2
4 dU
4 dL
4






















 mathematics
mathematics








