Similar presentations:
Методы решения тригонометрических уравнений. (Урок-лекция)
1.
2.
2 cos 2x cos x cos x2 cos 2x cos x cos x 0
cos x(2 cos 2 x 1) 0
или
2 cos 2x 1 0
cos x 0
1
cos 2 x
x n , n Z
2
Ответ:
6
k ,
2
2
1
2 x arccos 2 k , k Z
2
2 x 2 k , k Z
3
x k , k Z
6
n, k , n Z
3.
tgx(sin x 1) 0x из
n
Произведение равно 0, когда хотя бы
один
tgx 0 равен 0, аxдругой
n при
множителей
имеет
этом
x 2 k
смысл
2
sin x 1 0
sin x 1
sin
x
1
0
tgx 0 или
Ответ:
n,;n Z 2 k , n, k Z
x
n
2
x k , k Z
2
sin x 1
x 2 m, m Z
2
не соотв. условию
Ответ:
k , k Z
4.
3 cos x 10 cos x 3 02
cos x t , t 1;1
3t 2 10t 3 0
t1
1
, t2 3
3
не соот условию
1
cos x
3
1
x arccos 2 n
3
Ответ:
1
arccos 2 n, n Z
3
5.
cos 3x sin 3x 0: cos x 0
cos 3 x sin 3 x
0
cos 3 x cos 3x
1 tg 3 x 0
tg 3 x 1
3 x arctg 1 n
3x
x
4
12
n
n
3
Ответ:
12
n
3
,n Z
6.
2 cos x 3 sin x cos x sin x 02
2
: cos 2 x 0
2 cos 2 x 3 sin x cos x sin 2 x
0
2
2
2
cos x
cos x
cos x
3 sin x
2
tg 2 x 0
cos x
2 3tgx tg 2 x 0
tg 2 x 3tgx 2 0
x arctg 2 n
tgx t
t 3t 2 0
t1 2 t2 1
tgx 2 tgx 1
2
x arctg1 n
x
4
n
7.
6 sin x sin x cos x cos x 32
2
6 sin x sin x cos x cos x 3 cos x sin x 0
2
2
2
2
3 sin x sin x cos x 4 cos x 0 : cos x 0
2
2
3tg 2 x tgx 4 0
4
4
tgx , x arctg n
3
3
tgx 1, x k
4
Ответ:
4
k , arctg
n( n, k Z )
4
3
8.
3sin x 4 cos x 5Вынесем за скобку число
4
3
5 sin x cos x 5
5
5
3
4
sin x cos x 1
5
5
cos sin x sin cos x 1
sin x 1
x
2
32 42 5
Ответ:
3
arccos n, n Z
5 2
n
3
x n arccos n
2
5 2
4
arcsin n
5 2
9.
Проверить в исходном уравненииx 2 n
3sin x 4 cos x 5
x
2tg
1 tg 2
2 4
3
2 x
1 tg
1 tg 2
2
x
2 5
x
2
2t
1 t 2
3
4
5
2
2
1 t
1 t
6t
4 1 t 2
5
2
2
1 t
1 t
6t 4 4t 2 5 1 t 2
x
2 x
2tg
1 tg
2 , cos x
2
sin x
2 x
2 x
1 tg
1 tg
2
2
2
Пусть
x
tg t
2
1
x
1
t , tg
3
2
3
1
x 2arctg 2 n
3
Ответ:
1
2arctg 2 n, n Z
3
10.
cos 3x sin 2x sin 4x 0cos 3x sin 2 x sin 4 x 0
2x 4x
2x 4x
cos 3x 2 sin
cos
0
2
2
cos 3x 2 sin x cos 3x 0
cos 3x 1 2 sin x 0
n
cos 3x 0
x 6 3
k
1
2
sin
x
0
x 1 k
6
5
6
2
6
7
6
11
6
3
2
Ответ:
6
n
3
,n Z
11.
sin 5x cos 3x sin 6x cos 2x1
1
sin 8 x sin 2 x sin 8 x sin 4 x
2
2
sin 2 x sin 4 x 0
2x 4x
2x 4x
2 sin
cos
0
2
2
2 sin x cos 3x 0
sin x 0
x n
cos 3x 0
k
x 6 3
Ответ:
n,
6
k
3
( n, k Z )
12.
sin 2 x1 cos 2 x
1 cos 2 x
, cos 2 x
2
2
sin x sin 2 x 1
2
2
1 cos 2 x 1 cos 4 x
1
2
2
1 cos 2 x 1 cos 4 x 2
cos 2 x cos 4 x 0
2x 4x
2x 4x
2 cos
cos
0
2
2
2 cos 3 x cos x 0
Ответ:
6
n
3
,n Z
n
cos 3 x 0 x 6 3
cos x 0
x k
2
13.
Уравнение содержит набор sinx, cosx и sinxcosx
sin x cos x 1 sin x cos x
sin x cos x t sin x cos x t 2
2
2 2 x 2 sin x cos x t 2
sin 2 x cos
t 1
2
t 1
t 2 2t 1 0 t 1 0 2 t 1
2
t 1
1 2 sin x cos x t 2 sin x cos x
sin x cos x 1
2
1
1
2
sin x
cos x 1
2
2
1
cos sin x sin cos x
4
4
2
2
n
sin x
x 1 n
4 2
4 4
14.
5xsin
cos x 2
4
5x
5x
sin
1
2
n
4
4
2
cos x 1
x 2 k
, (n, k Z )
2 8 n
2 k
5
5
1 4n
т.к. к – целое число,то
k
5
n 1 5m (m Z )
x 2 8 m (m Z )
15.
f ( x ) g ( x)Равносильный переход:
1 cos x sin x
g ( x) 0
2
f ( x) g ( x)
sin x 0
2
1 cos x sin x
sin x cos x 1 0
2
1 cos x cos x 1 0
cos x(cos x 1) 0
2
x
2
k
x 2 n
Ответ:
не соотв усл
x
2
2 k , 2 n, k , n Z






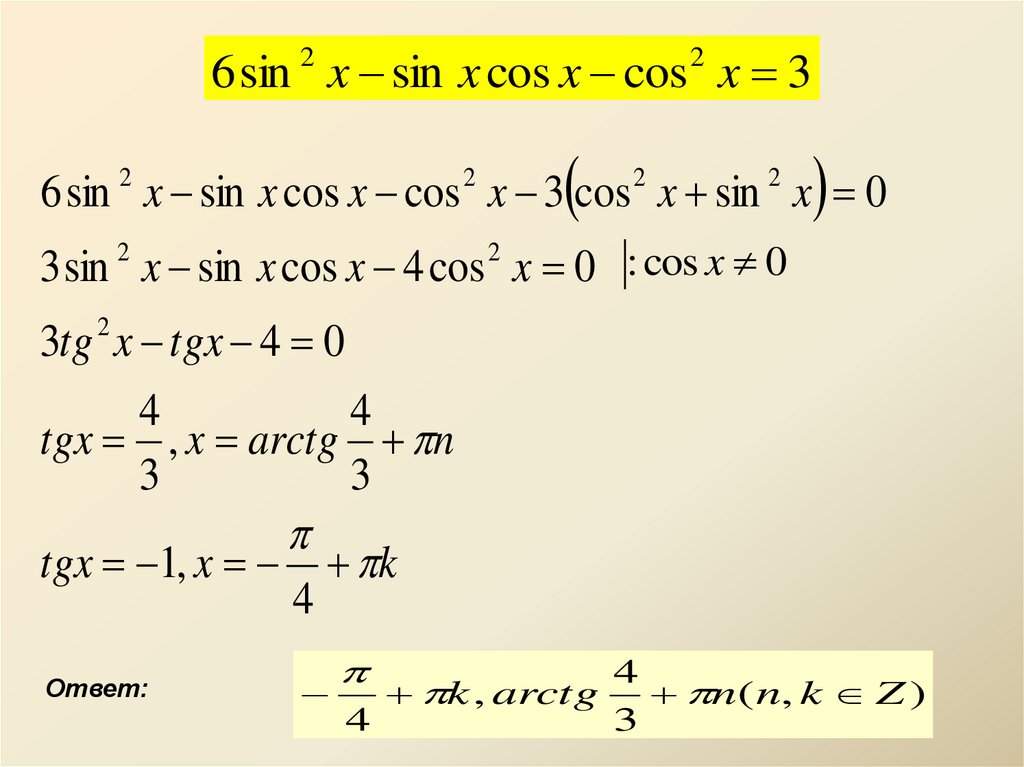








 mathematics
mathematics








