Similar presentations:
Analýza kvalitativních znaků_vzorove priklady
1.
Příklad tabulka 2x2:U 120 zaměstnanců byl zjišťován zájem o pokročilý kurz
informatiky. Výsledky průzkumu byly sestaveny do
asociační tabulky:
Nejprve se provede testování, kdy chceme odpovědět na
otázku, zda zájem o kurz je ovlivněn pohlavím ( = 0,05).
Protože n > 40, použijeme rovnou 2 – test.
2.
H0: zájem o kurz není ovlivněn pohlavímH1: zájem o kurz je ovlivněn pohlavím
2
n
a
d
b
c
120
(
50
43
13
14
)
2
36,1117
a b a c b d c d
63 57 64 56
2
02, 05 (1) 3,841
viz tab. str.182-184
2 2 H 0 se zamítá
V případě prokázané závislosti mezi znaky je možné
zjistit sílu závislosti.
3.
V2
n
Koeficient asociace
n a a b a c
120 50 63 64
V
0,5486
a b c d a c b d
63 57 64 56
Závislost mezi zájmem o kurz informatiky a pohlavím
zaměstnanců je středně silná.
4.
Příklad tabulka 2x2 Fisherův faktoriálový test:U 27 náhodně vybraných pracovníků s VŠ vzděláním bylo
zjišťováno, zda mají zájem o další zvyšování vzdělání
formou postgraduálního studia. V souboru byli muži i
ženy. Výsledky byly sestaveny do tabulky:
Pohlaví
muž
žena
celkem
Zájem o studium
ano
ne
9
8
3
7
12
15
celkem
17
10
27
Zajímá nás, zda zájem o studium je ovlivněn pohlavím pracovníků. Protože rozsah souboru
je 27, tzn. v rozmezí 20 – 40, je třeba vypočítat teoretické četnosti, abychom zjistili
použitelnost 2 – testu.
H0: zájem o studium nezávisí na pohlaví pracovníků
H1: zájem o studium závisí na pohlaví pracovníků
5.
(a b)(a c)a0
n
c0
(c d )(a c)
n
(a b)(b d)
b0
n
(c d)(b d)
d0
n
17 12
a0
7,55
27
17 15
b0
9,44
27
10 12
c0
4,44
27
10 15
d0
5,55
27
Jestliže alespoň jedna z
očekávaných četností je
menší než 5, je nutno
použít Fisherův
faktoriálový test.
6.
Vytváříme pomocné tabulky, kdy nejmenší četnost vždy zmenšujeme o jedna.I.
9
3
12
8
7
15
17
10
27
II.
10
2
12
7
8
15
17
10
27
III.
11
1
12
6
9
15
17
10
27
IV.
12
0
12
5
10
15
17
10
27
7.
pia b ! c d ! a c ! b d !
n! a ! b! c! d !
8.
pia b ! c d ! a c ! b d !
n! a ! b! c ! d !
17 !10 !12 !15 !
pI
0,167810831
27 ! 9! 3! 8! 7 !
9
3
12
17 !10 !12 !15 !
p II
0,050343249
27 ! 10 ! 2 ! 7 ! 8!
10
2
12
17 !10 !12 !15 !
p III
0,0071192473 94
27 ! 11! 1! 6 ! 9 !
p IV
= 0,05
12
0
12
17
10
27
7
8
15
11
1
12
17 !10 !12 !15 !
0,0003559623697
27 ! 12 ! 0 ! 10 ! 5!
p p i 0,225629289
17
10
27
8
7
15
17
10
27
6
9
15
5
10
15
17
10
27
0,2256 > 0,05 H0 se přijímá, tzn., nelze potvrdit, že by zájem pracovníka o
studium byl ovlivněn pohlavím.
9.
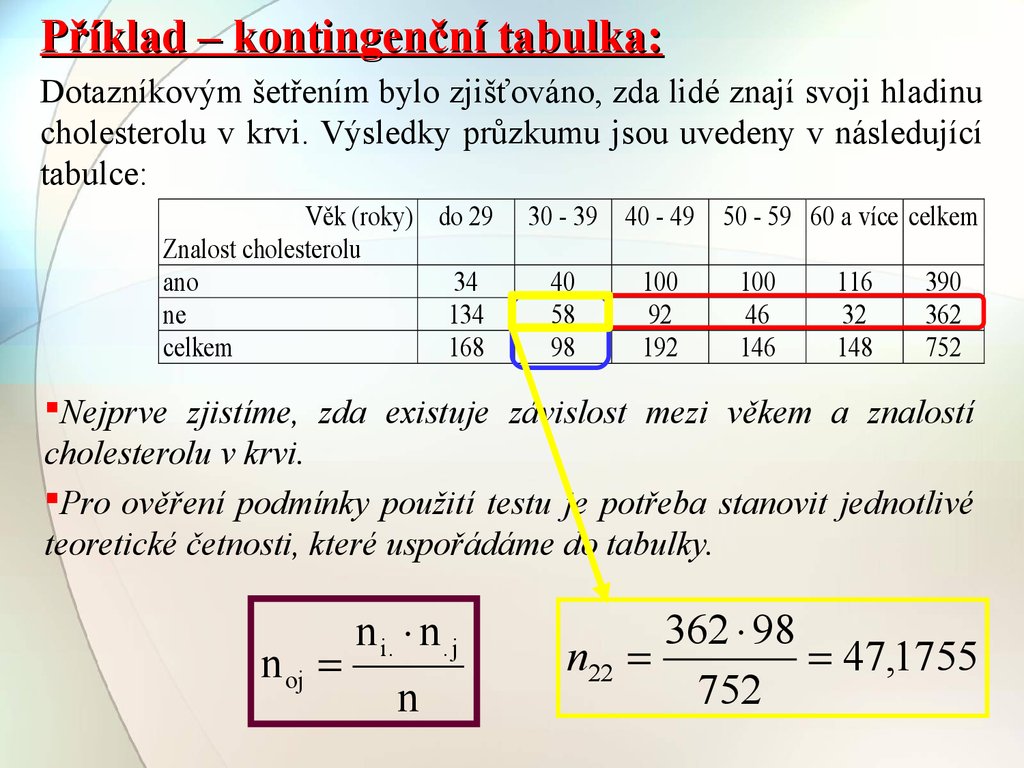
Příklad – kontingenční tabulka:Dotazníkovým šetřením bylo zjišťováno, zda lidé znají svoji hladinu
cholesterolu v krvi. Výsledky průzkumu jsou uvedeny v následující
tabulce:
Věk (roky) do 29
Znalost cholesterolu
ano
34
ne
134
celkem
168
30 - 39 40 - 49
40
58
98
100
92
192
50 - 59 60 a více celkem
100
46
146
116
32
148
390
362
752
Nejprve zjistíme, zda existuje závislost mezi věkem a znalostí
cholesterolu v krvi.
Pro ověření podmínky použití testu je potřeba stanovit jednotlivé
teoretické četnosti, které uspořádáme do tabulky.
n oj
n i. n . j
n
362 98
n22
47,1755
752
10.
rs
2
n nij
ni .n. j
i 1 j 1
r
s
2
n
2
ij n oj
i 1 j 1
n
Dvě možnosti stanovení
hodnoty testovacího kritéria 2
2
n oj
nij – dílčí absolutní četnosti odpovědí – skutečné četnosti
Věk (roky) do 29
Znalost cholesterolu
ano
34
ne
134
celkem
168
30 - 39
40 - 49
40
58
98
100
92
192
50 - 59 60 a více celkem
100
46
146
116
32
148
390
362
752
noj – očekávané (teoretické) četnosti odpovědí
n oj
n i. n . j
n
Věk (roky)
Znalost cholesterolu
ano
ne
do 29
30 - 39
40 - 49
87,13
80,87
50,82
47,18
99,57
92,43
50 - 59 60 a více
75,72
70,28
76,76
71,24
11.
H0: znalost hladiny cholesterolu není ovlivněna věkemH1: znalost hladiny cholesterolu je ovlivněna věkem
12.
Věk (roky)Znalost cholesterolu
ano
ne
r
s
2
i 1 j 1
2
n
do 29
30 - 39
40 - 49
87,13
80,87
50,82
47,18
99,57
92,43
ij n oj
50 - 59 60 a více
75,72
70,28
76,76
71,24
2
n oj
2
2
2
2
2
2
34 87,13
40 50,82
100 99,57
100 75,72
116 76,76
134 80,87
87,13
50,82
99,57
75,72
2
2
2
2
58 47,18
92 92,43
46 70,28
32 71,24
47,18
92,43
2 2 1 . 5 1
0 , 01
70,28
13,277
viz tab. str.182-184
71,24
76,76
80,87
129,949
H 0 se zamítá
2
2
13.
Závěr: Mezi oběma kvalitativními znaky bylaprokázána závislost (vysoce významná). S
pravděpodobností 99 % je znalost hladiny
cholesterolu vysoce významně ovlivněna věkem
člověka.
Po provedení tohoto testu je možné stanovit sílu
závislosti mezi sledovanými znaky.
2
129, 949
C
0,38385
2
n
752 129, 949
Jedná se o středně silnou závislost.






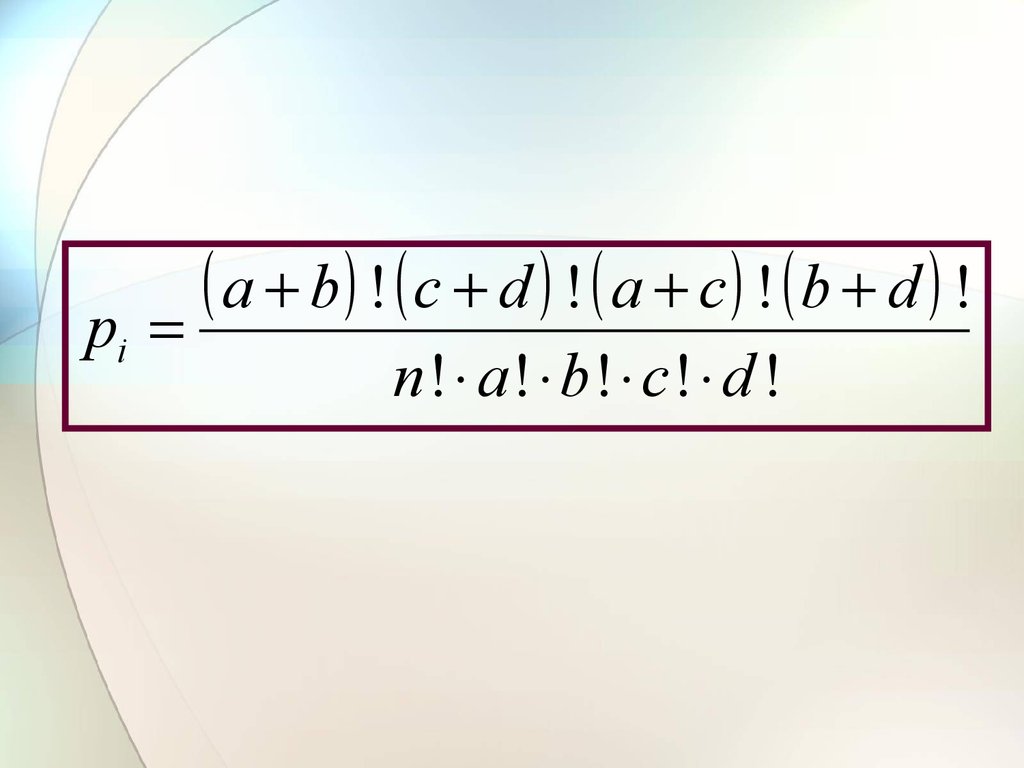





 mathematics
mathematics








