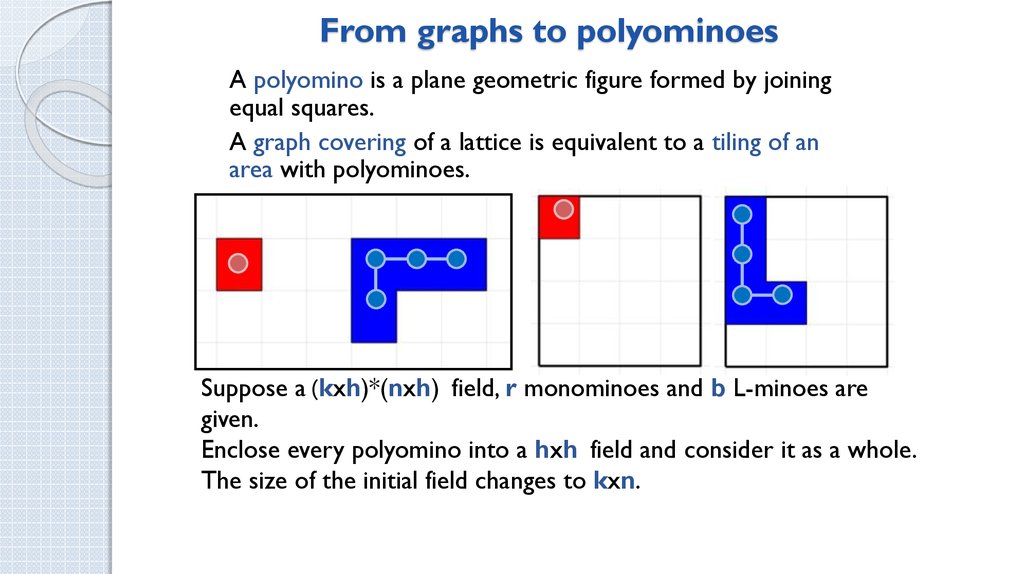
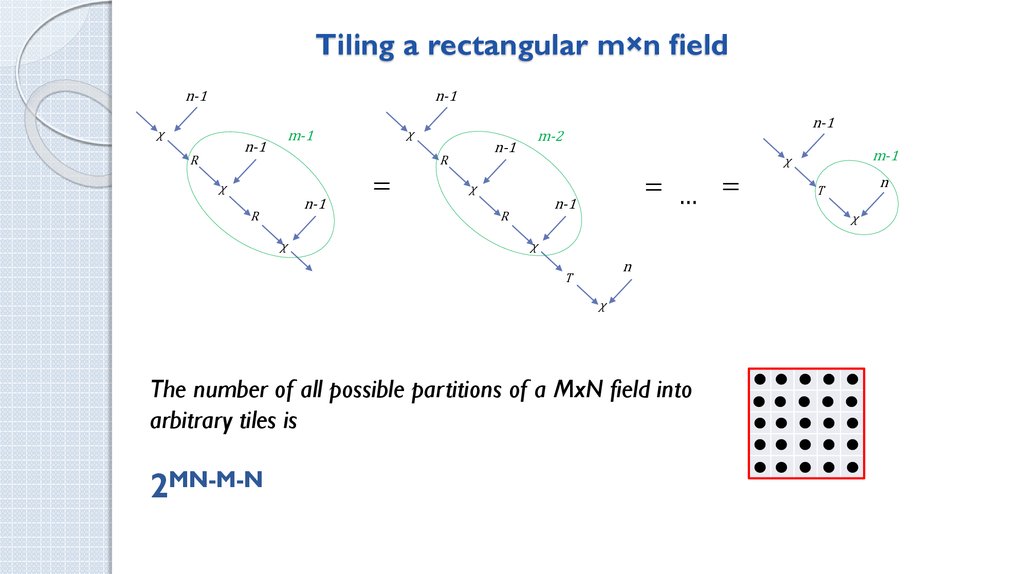
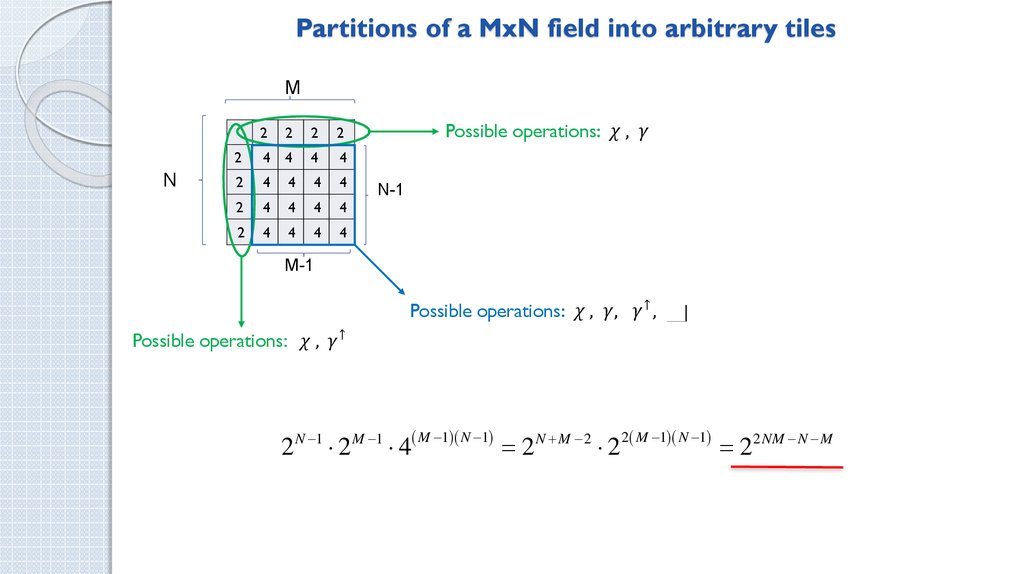
How many ways are there to tile a rectangle with polyominoes?

1. How many ways are there to tile a rectangle with polyominoes?

Aleksandrov N.M., Askerova A.A., Dzhuraev A.A., Kaniber
V.V., Kruzhkov D.O., Raeva A.A., Stolbova V.A.
Bauman Moscow State Technical University, Moscow,
Russia

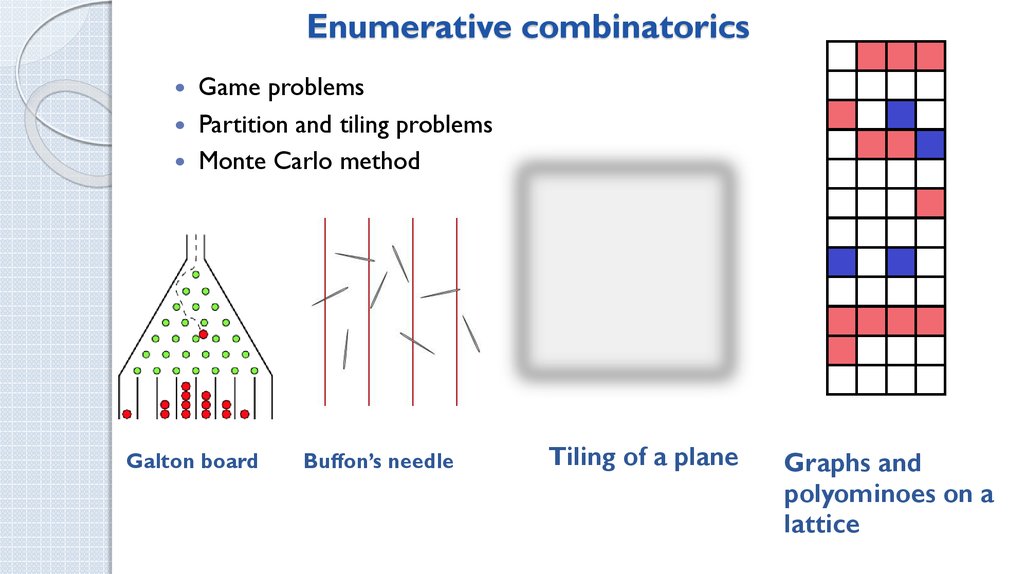
2. Enumerative combinatorics

Game problems
Partition and tiling problems
Monte Carlo method
Galton board
Buffon’s needle
Tiling of a plane
Graphs and
polyominoes on a
lattice

3. Random walks on a lattice

If some atoms fit into two
squares with adjacent sides, a
“spring” appears between
them.
Percentage of draws
Number of springs

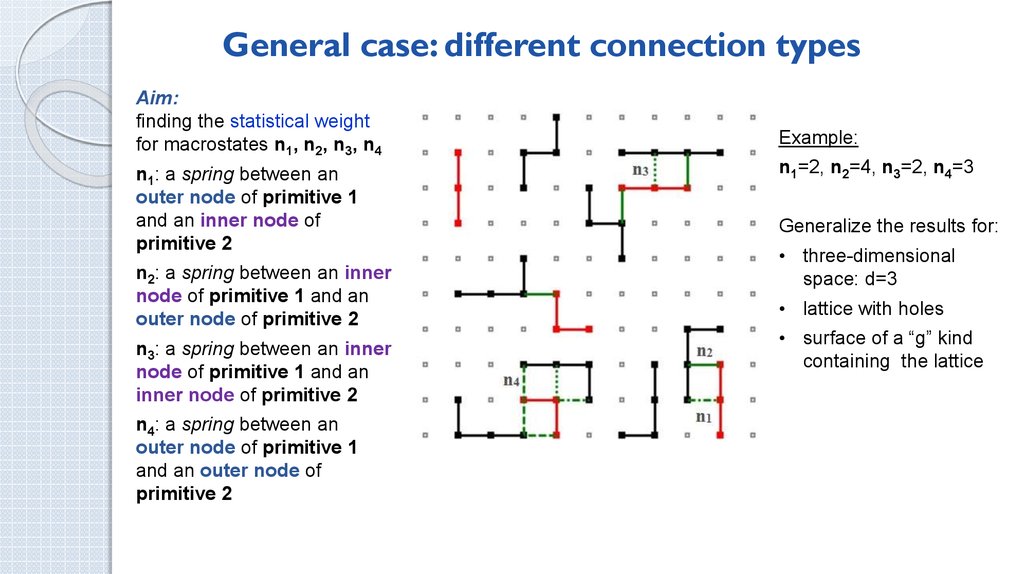
4. General case: different connection types

Aim:
finding the statistical weight
for macrostates n1, n2, n3, n4
n1: a spring between an
outer node of primitive 1
and an inner node of
primitive 2
n2: a spring between an inner
node of primitive 1 and an
outer node of primitive 2
n3: a spring between an inner
node of primitive 1 and an
inner node of primitive 2
n4: a spring between an
outer node of primitive 1
and an outer node of
primitive 2
Example:
n1=2, n2=4, n3=2, n4=3
Generalize the results for:
• three-dimensional
space: d=3
• lattice with holes
• surface of a “g” kind
containing the lattice

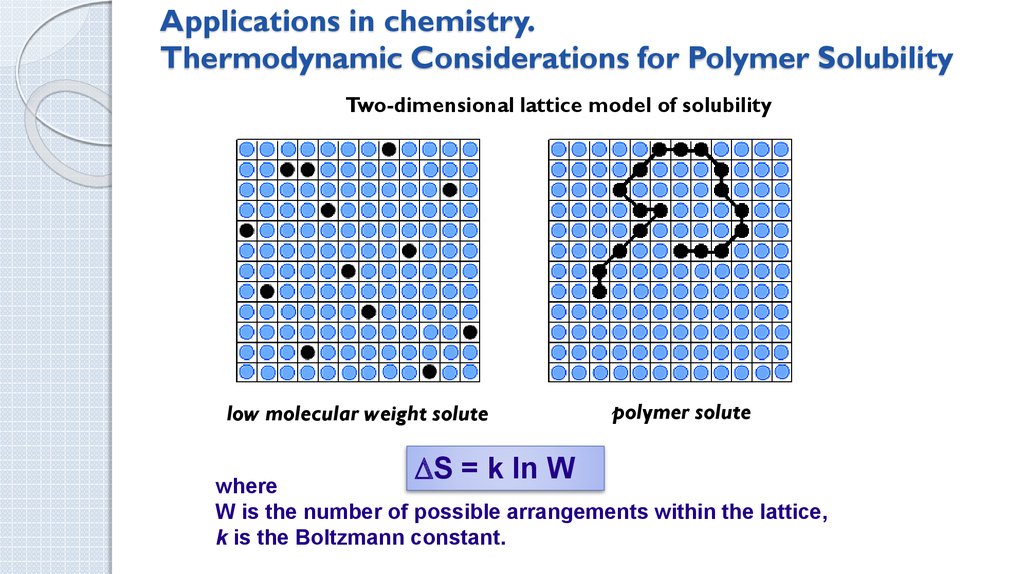
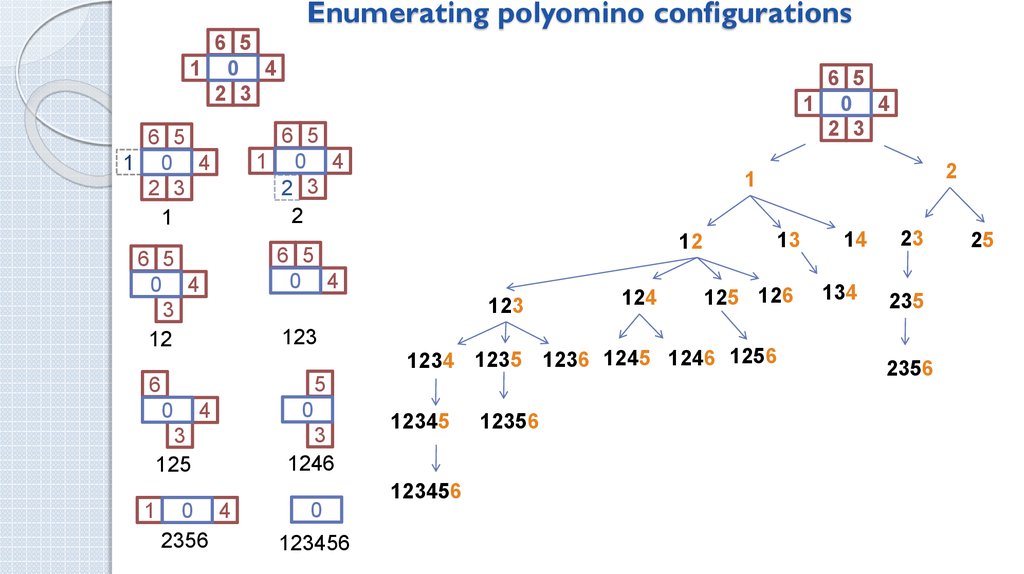
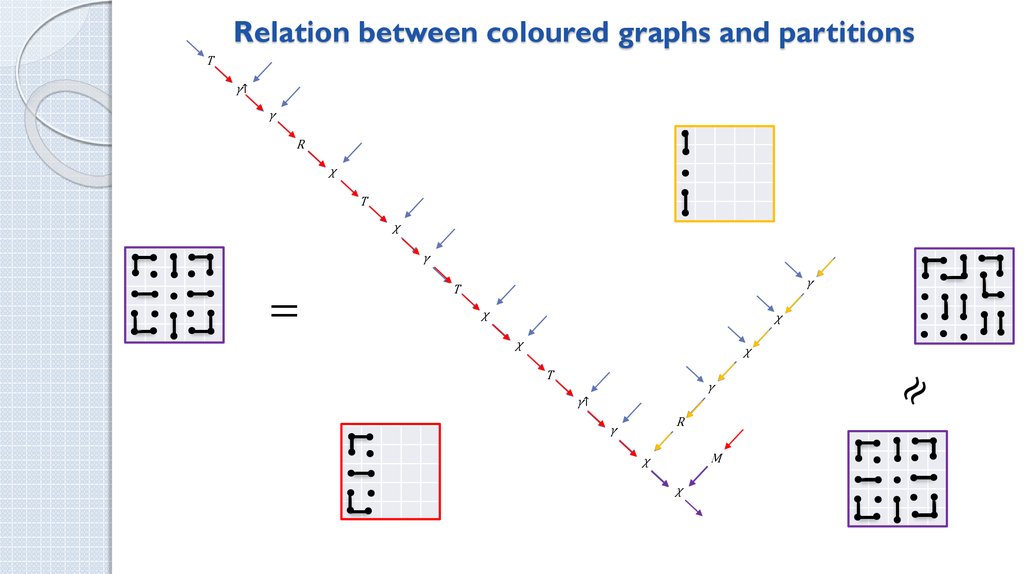
5. Statistical weight problem for a system of graphs embedded in square lattice

1
2
…
MxN
nodes
1 2
…
M
N
1
• How many realizations of an
ordered set (n1, n2,…, nS)
exist at fixed number of
nodes and kind of graphs?
• ns (