Термодинамические циклы. Понятие о круговом процессе (цикле). Прямые и обратные циклы

1.

ТЕРМОДИНАМИЧЕСКИЕ ЦИКЛЫ
ПОНЯТИЕ О КРУГОВОМ ПРОЦЕССЕ (ЦИКЛЕ).
ПРЯМЫЕ И ОБРАТНЫЕ ЦИКЛЫ
Циклом называется замкнутый круговой процесс, при осуществлении которого
рабочее тело, пройдя ряд последовательных состояний, возвращается в исходное.
Прямой цикл − тепловые машины, двигатели.
Обратный цикл − холодильные машины, тепловые насосы.
l ц pdv
l ц q1 q 2
pdv pdv
1a 2
2b1
(1)
Термодинамическим
КПД
называется
отношение работы цикла к подведённой
теплоте.
lц
q1
(2)
q2
t 1
q1
(3)
t

2.

Среднее давление цикла
lц
pt
v max v min
v max v min vh − рабочий объём цикла
(4)
Среднее давление цикла представляет собой удельную работу цикла.
q1
t
v min 1
v max
− степень сжатия
v min
v min − объём камеры сгорания (или сжатия)
q1
− тепловая нагрузка единицы объёма камеры сгорания
v min
pt
(5)
В холодильной установке полезным эффектом является теплота, отданная от
объекта охлаждения в холодильной камере q2. Отношение этой величины к
затраченной работе называется холодильным коэффициентом.
q2
lц
(6)

3.

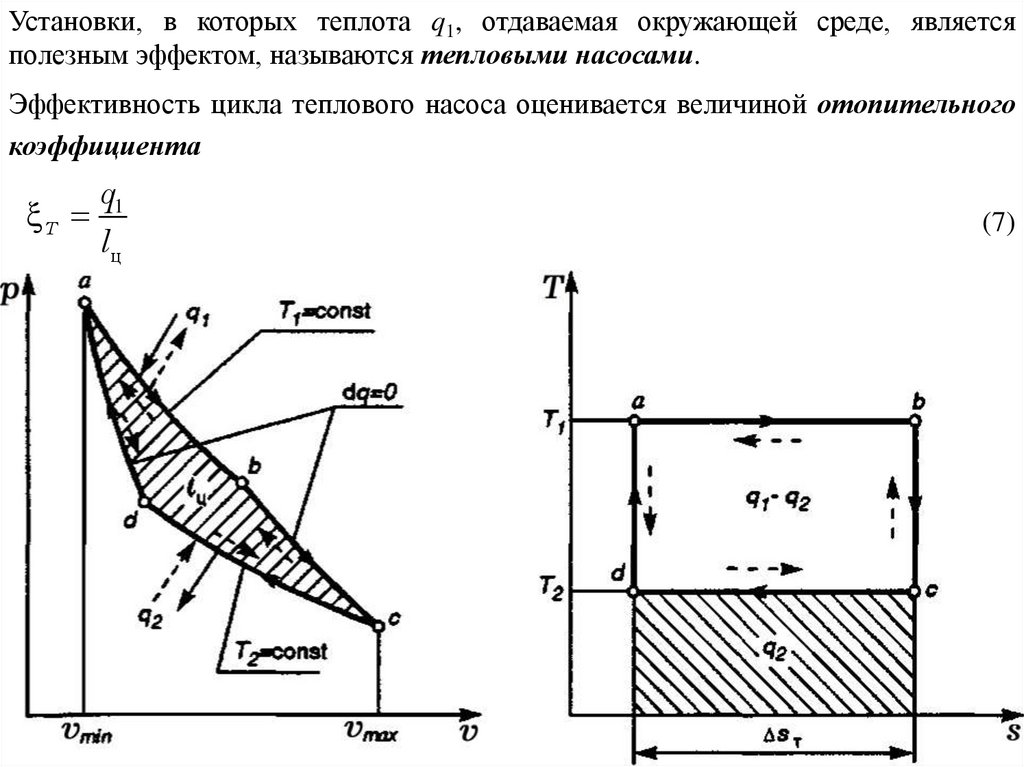
Установки, в которых теплота q1, отдаваемая окружающей среде, является
полезным эффектом, называются тепловыми насосами.
Эффективность цикла теплового насоса оценивается величиной отопительного
коэффициента
T
q1
lц
(7)

4.

vb
q1 RT1 ln
va
vc v max
T1 sT
T1
vb
T2
vc
q 2 RT2 ln
vd
(8)
1
k 1
T2 sT
(9)
vb v c
T − степень изотермического сжатия (расширения)
va vd
t 1
T2
T1
(10)
Среднее давление цикла Карно
pt
pmax ln T
T (1 t )
( k 1) 1
1
t
(11)

5.

Холодильный коэффициент обратного цикла Карно
T2
1
T1 T2 T1 1
T2
(12)
Отопительный коэффициент теплового насоса, работающего по обратному циклу
Карно
T1
1
T
T1 T2 1 T2
T1
(13)

6.

ЦИКЛЫ ПОРШНЕВЫХ ДВИГАТЕЛЕЙ ВНУТРЕННЕГО
СГОРАНИЯ
Термодинамический цикл поршневого двигателя внутреннего сгорания (ПДВС)
представляет собой повторяющуюся замкнутую последовательность обратимых
термодинамических процессов, каждый из которых приближённо отражает
известные из опыта особенности реальных процессов, происходящих в
работающем двигателе.
Цикл совершается неизменным количеством рабочего тела, которое будем
полагать идеальным газом постоянного состава с теплоёмкостью, независящей от
температуры.
Задача термодинамического исследования циклов ПДВС состоит в получении
выражений термического КПД и среднего давления цикла, а также выявлении
характера зависимости этих показателей от параметров цикла.
В общем случае термический КПД и среднее давление цикла зависят от степени
сжатия, природы рабочего тела, количества подведённой теплоты и способа её
подвода.

7.

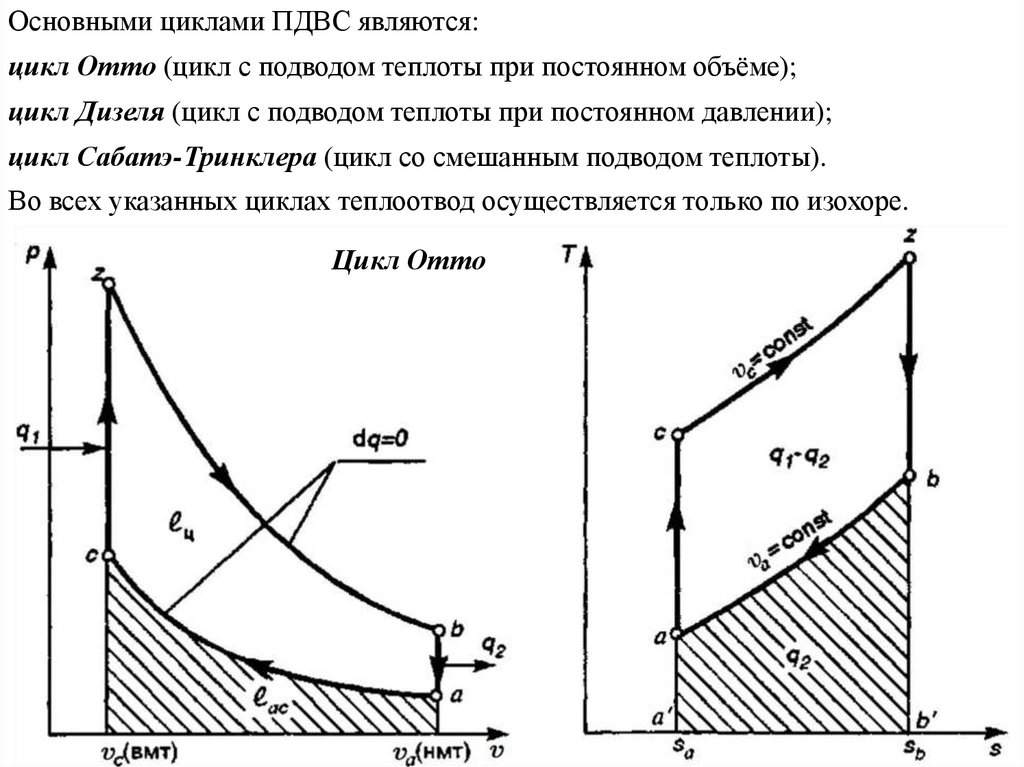
Основными циклами ПДВС являются:
цикл Отто (цикл с подводом теплоты при постоянном объёме);
цикл Дизеля (цикл с подводом теплоты при постоянном давлении);
цикл Сабатэ-Тринклера (цикл со смешанным подводом теплоты).
Во всех указанных циклах теплоотвод осуществляется только по изохоре.
Цикл Отто

8.

va
− степень сжатия
vc
pz
− степень повышения давления при изохорном теплоотводе
pc
q1 c v (Tz Tc ) − подведённая теплота
q 2 c v (Tb Ta ) − отведённая теплота
q
T Ta
t 1 2 1 b
q1
Tz Tc
(14)
Выразим температуры в характерных точках цикла через его параметры и
начальную температуру Ta
Tc Ta
t 1
k 1
1
k 1
Tz Tc Ta k 1
Tb
Tz
Ta
k 1
(15)
Таким образом, термический КПД цикла с подводом теплоты при постоянном
объёме зависит только от степени сжатия и природы рабочего тела.

9.

Из уравнения (15) видно, что для рассматриваемого цикла, термический КПД тем
больше, чем больше степень сжатия.
Однако если при малых степенях сжатия
повышение ε вызывает существенное
увеличение термического КПД, то при
высоких значениях ε возрастание ηt при
увеличении ε делается всё менее и менее
значительным (см. рис.).
С уменьшением показателя адиабаты
термический КПД при той же степени
сжатия уменьшается.
В реальном двигателе искрового
зажигания выбор степени сжатия в
основном определяется практическими
возможностями организации процесса
сгорания без детонации. Так как в
уравнении (15) отсутствует параметр λ,
то термический КПД цикла Отто не
зависит от количества подведённой
теплоты, т.е. от нагрузки.
Зависимость показателей цикла
Отто от степени сжатия при
ограничении на максимальную
температуру цикла (pa = 0,1 МПа,
Ta = 300 К, Tz = 2700 К, k = 1,4).

10.

Среднее давление цикла определяемое по выражению (5), которое с учётом того,
что
q1 c vTa k 1 ( 1)
pa k ( 1)
pt
t
(k 1)( 1)
cv
R
k 1
(16)
При прочих равных условиях pt возрастает прямо пропорционально
начальному давлению цикла pa.
На практике повышение pa осуществляют за счет применения наддува. В
бензиновых двигателях давление наддува ограничено возникновением детонации.
Среднее давление цикла повышается с увеличением количества теплоты (ростом
λ = Tz/Tc). Однако, если на максимальную температуру цикла Tz наложено
ограничение, связанное, например, с требованием уменьшения выбросов оксидов
азота NOx, то, как показывают расчёты, кривая среднего давления цикла в
функции от степени сжатия проходит через максимум (см. рис.).

11.

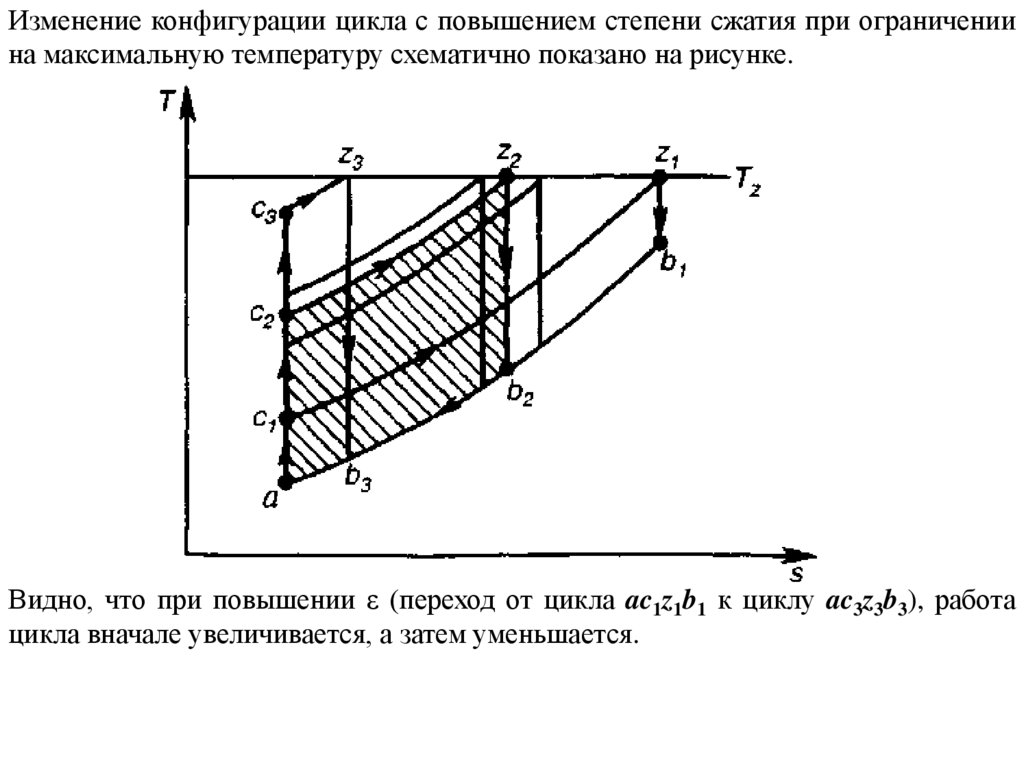
Изменение конфигурации цикла с повышением степени сжатия при ограничении
на максимальную температуру схематично показано на рисунке.
Видно, что при повышении ε (переход от цикла ac1z1b1 к циклу ac3z3b3), работа
цикла вначале увеличивается, а затем уменьшается.

12.

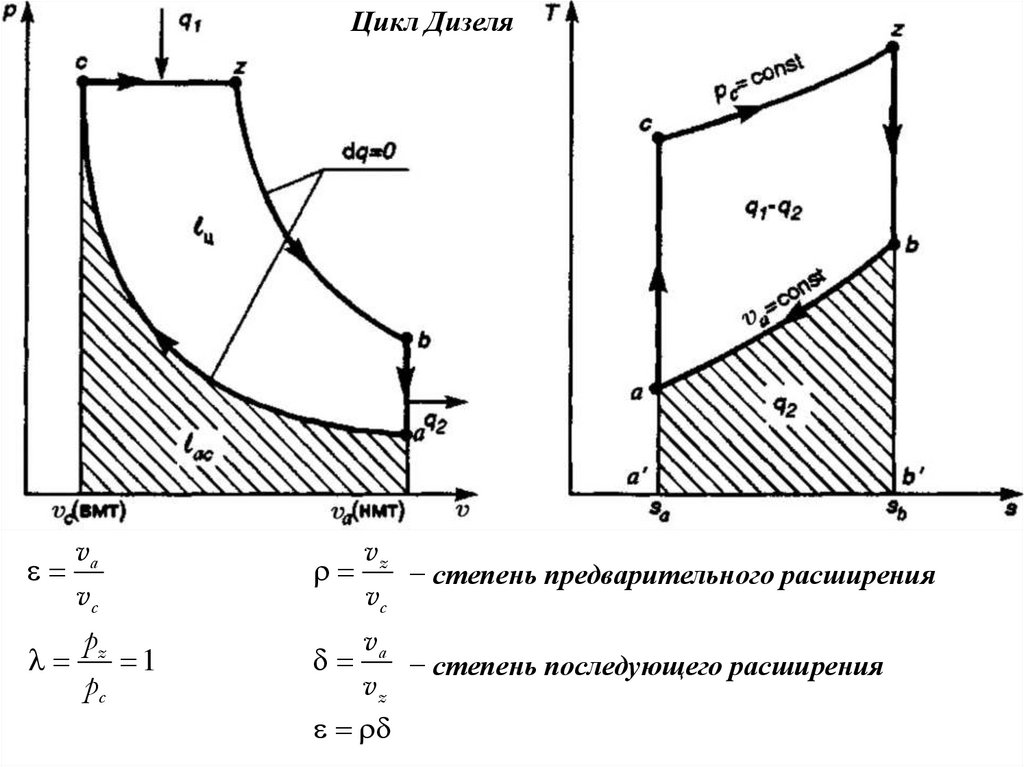
Цикл Дизеля
va
vc
p
z 1
pc
vz
− степень предварительного расширения
vc
v
a − степень последующего расширения
vz

13.

Выразим температуры в характерных точках цикла через его параметры и
начальную температуру Ta
Tc Ta
k 1
Tz Tc Ta
k 1
Tz
Tz k 1
Tb k 1 k 1 Ta k
В соответствии с полученными соотношениями
q1 c p (Tz Tc ) c p k 1Ta ( 1)
(17)
q 2 c v (Tb Ta ) c v Ta ( k 1)
Подставляя эти результаты в (3), получим
1 k 1
t 1 k 1
k ( 1)
(18)
Из (17) следует, что тепловую нагрузку в цикле Дизеля отражает параметр ,
который находится по формуле
q1
1
c pTa k 1
(19)
pa k k ( 1)
pt
t
(k 1)( 1)
(20)

14.

Таким образом, как и в случае цикла Отто, ηt и pt цикла Дизеля зависят от
природы рабочего тела и степени сжатия, возрастая при повышении ε и
показателя адиабаты k.
В отличии от цикла Отто, в данном случае термический КПД зависит от тепловой
нагрузки цикла, т.е. количества подведённой теплоты. С его увеличением ηt
снижается. По условию организации теплоотвода по изохоре ba величина не
может превышать значения ε. Несмотря на снижение ηt, увеличение количества
подводимой теплоты приводит к росту среднего давления цикла.
Традиционно цикл с подводом теплоты при p = const считается термодинамическим циклом тихоходного дизеля. Однако при подборе подходящих значений
pa и ε этот цикл может рассматриваться как модель цикла двигателя с искровым
зажиганием при его работе на особо малых нагрузках и холостом ходу.

15.

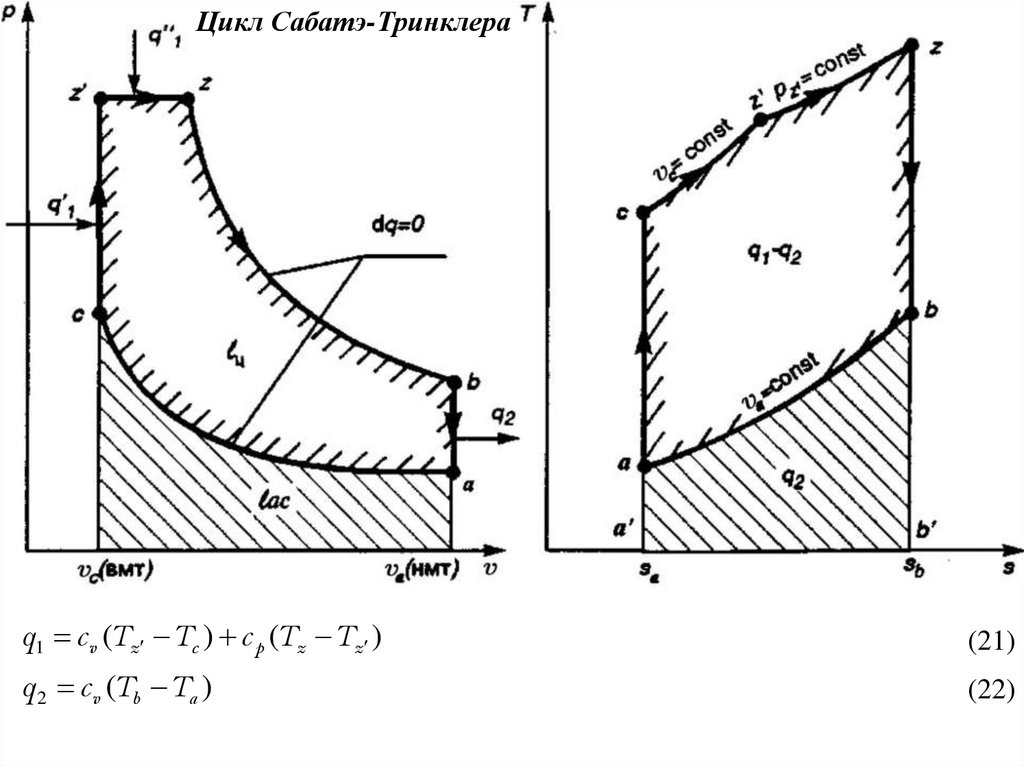
Цикл Сабатэ-Тринклера
q1 c v (Tz Tc ) c p (Tz Tz )
(21)
q 2 c v (Tb Ta )
(22)

16.

q1 c vTa k 1 1 k ( 1)
(23)
q 2 c vTa ( k 1)
(24)
k 1
t 1 k 1
1 k ( 1)
pa k [ 1 k ( 1)]
pt
t
(k 1)( 1)
xq
1 v 1k 1
c vTa
(1 xv )q1
1
k (c vTa k 1 xv q1 )
q1
xv
− доля теплоты, подведённой в изохорном процессе
q1
1
(25)
(26)
(27)
(28)

17.

ЦИКЛЫ ГАЗОТУРБИННЫХ ДВИГАТЕЛЕЙ
В цикле газотурбинного двигателя (ГТД) процессы осуществляются в разных
элементах двигателя одновременно при непрерывном или пульсирующем потоке
через них рабочего тела.
В цикле ГТД с непрерывным потоком теплота к рабочему телу подводится при
постоянном давлении (p = const), в цикле с пульсирующим потоком подвод
теплоты осуществляется при постоянном объёме (V = const).
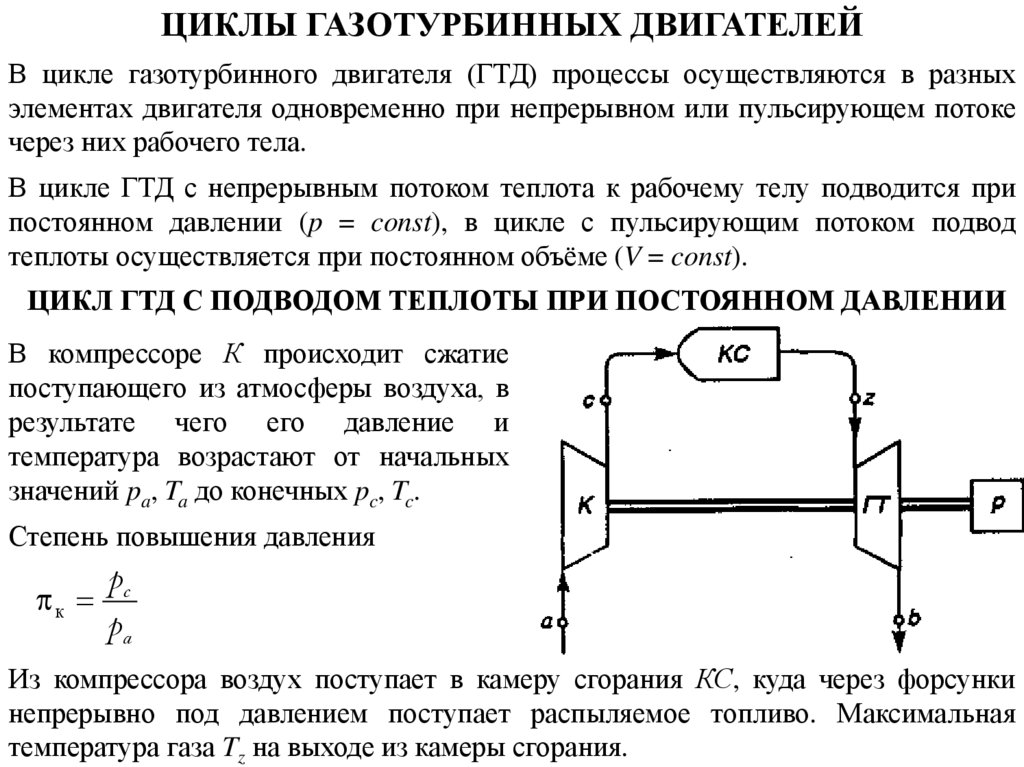
ЦИКЛ ГТД С ПОДВОДОМ ТЕПЛОТЫ ПРИ ПОСТОЯННОМ ДАВЛЕНИИ
В компрессоре К происходит сжатие
поступающего из атмосферы воздуха, в
результате чего его давление и
температура возрастают от начальных
значений pa, Ta до конечных pc, Tc.
Степень повышения давления
pc
к
pa
Из компрессора воздух поступает в камеру сгорания КС, куда через форсунки
непрерывно под давлением поступает распыляемое топливо. Максимальная
температура газа Tz на выходе из камеры сгорания.

18.

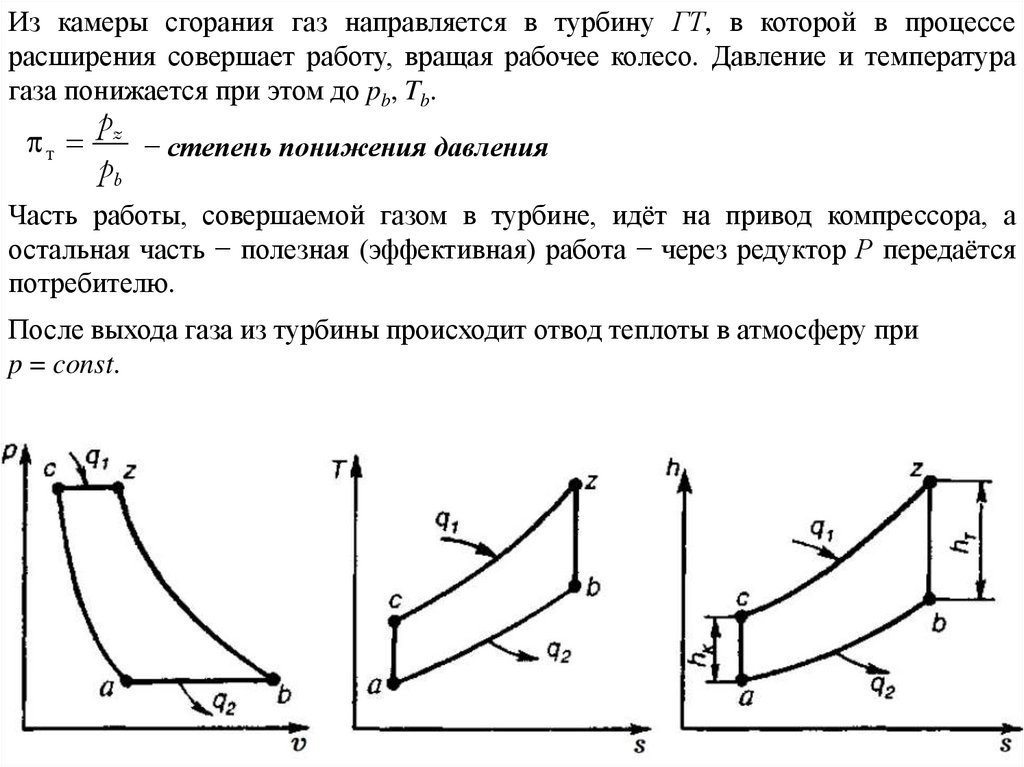
Из камеры сгорания газ направляется в турбину ГТ, в которой в процессе
расширения совершает работу, вращая рабочее колесо. Давление и температура
газа понижается при этом до pb, Tb.
т
pz
− степень понижения давления
pb
Часть работы, совершаемой газом в турбине, идёт на привод компрессора, а
остальная часть − полезная (эффективная) работа − через редуктор Р передаётся
потребителю.
После выхода газа из турбины происходит отвод теплоты в атмосферу при
p = const.

19.

В изобарных процессах подвод и отвод теплоты
q1 c p (Tz Tc )
q 2 c p (Tb Ta )
Тогда при условии cp = const, термический КПД цикла
q2
Tb Ta
t 1 1
q1
Tz Tc
(29)
Выразим температуры газов в переходных точка цикла через температуру Ta.
k 1
k
k 1
Tc pc
к k
Ta pa
Tz vz
Tc vc
Tb pb
Tz pz
k 1
k
pa
pc
Tc Ta
k 1
k
к
k 1
k
к
Tz Tc Ta
k 1
k
1
k 1
k
к
Tb
Tz
k 1
k
к
Ta
vz
− степень предварительного расширения
vc

20.

Подставив полученные выражения температур в уравнение (29), получим
t 1
1
k 1
k
к
(30)
Удельная работа цикла lц определяется как разность между работой lт расширения
в турбине и работой lк сжатия в компрессоре.
l ц l т l к (hz hb ) (hc ha ) c p (Tz Tb ) c p (Tc Ta )
k
R Tz (1 Tb Tz ) Ta (Tc Ta 1)
k 1
После замены отношений температур соответствующими отношениями давлений
имеем
1 k
1 k
k
k
k
lц
RTa 1 к к 1
k 1
T
z − степень повышения температуры в цикле
Ta
(31)

21.

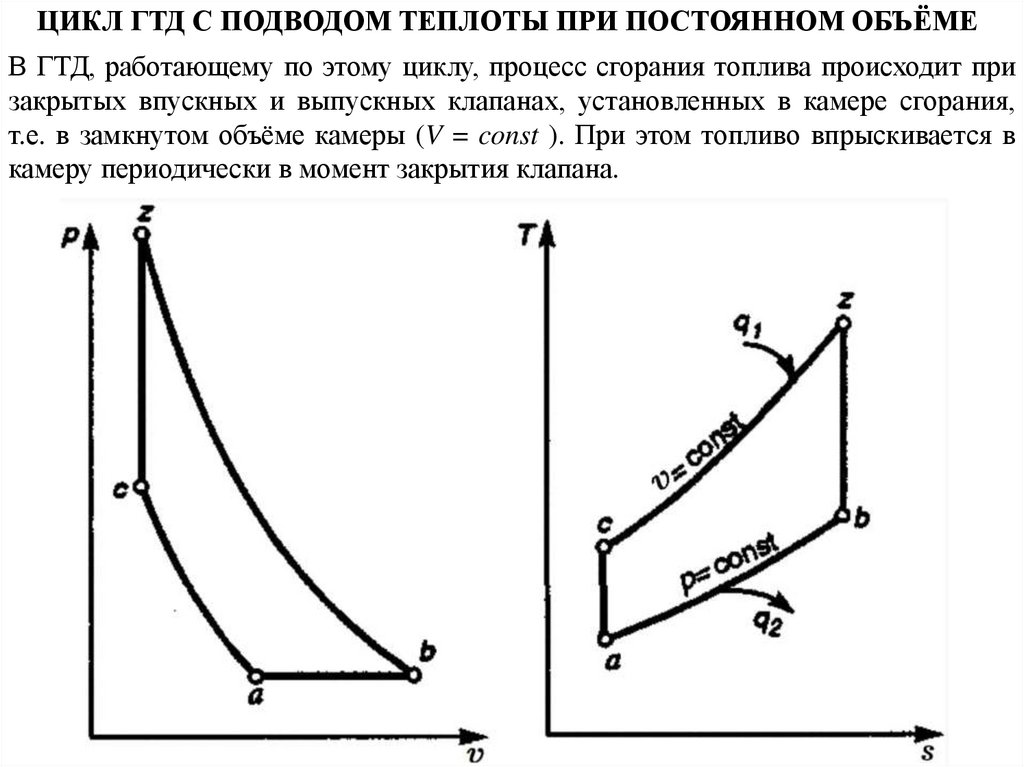
ЦИКЛ ГТД С ПОДВОДОМ ТЕПЛОТЫ ПРИ ПОСТОЯННОМ ОБЪЁМЕ
В ГТД, работающему по этому циклу, процесс сгорания топлива происходит при
закрытых впускных и выпускных клапанах, установленных в камере сгорания,
т.е. в замкнутом объёме камеры (V = const ). При этом топливо впрыскивается в
камеру периодически в момент закрытия клапана.

22.

Количество теплоты, подводимой к рабочему телу в этом цикле, определяется
выражением
q1 c v (Tz Tc )
Термический КПД цикла равен
c p (Tb Ta )
q2
t 1 1
q1
c v (Tz Tc )
Выразим температуры в характерных точках цикла через Ta:
Tc Ta
k 1
k
к
Tz Ta
k 1
k
к
Tb Ta
1
k
pz
− степень изохорного повышения давления при подводе теплоты
pc
t 1
1
k
k ( 1)
k 1
k
к
(32)
( 1)
Таким образом, термический КПД цикла с подводом теплоты при V=const зависит
как от степени повышения давления к в компрессоре, так и от количества
подведённой к циклу теплоты q1, которому соответствует определённое значение
величины .

23.

В изохорном процессе подвода теплоты
pz Tz
Tz
pc Tc Ta (кk 1) k к(k 1) k
k 1 k (кk 1) k
t 1 (k 1) k 2
(k 1) k
к
к
2
(33)
Удельная работа за цикл определяется выражением
R
l ц q1 t cv (Tz Tc ) t
Ta к(k 1) k t
k 1
(34)

24.

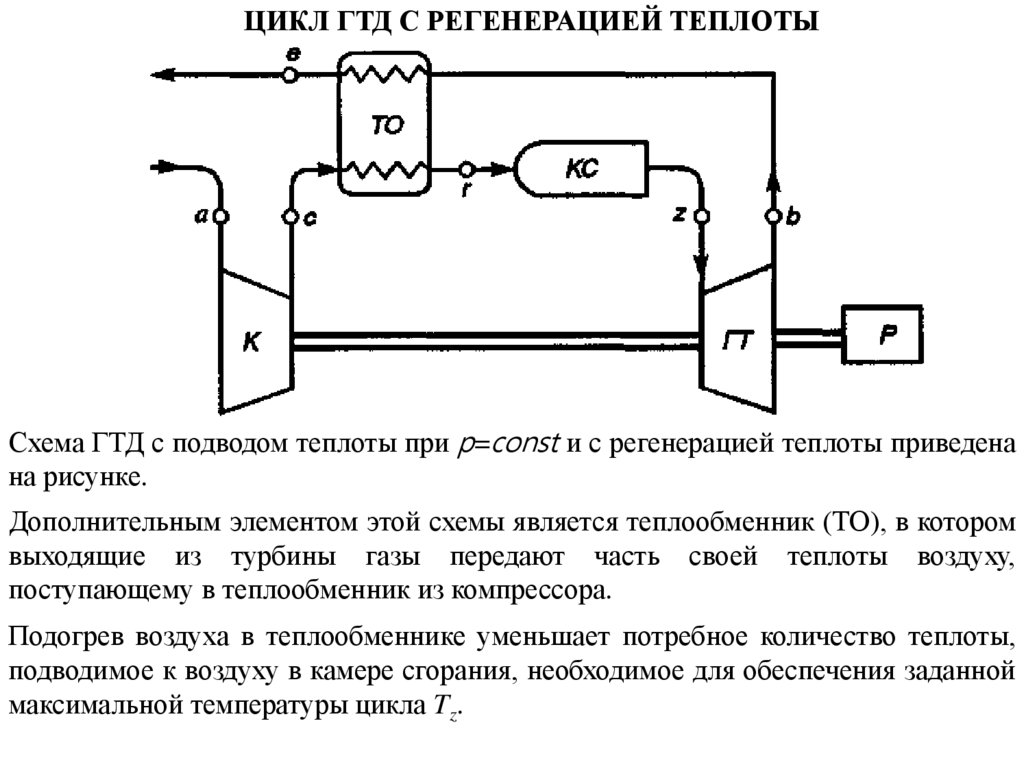
ЦИКЛ ГТД С РЕГЕНЕРАЦИЕЙ ТЕПЛОТЫ
Схема ГТД с подводом теплоты при p=const и с регенерацией теплоты приведена
на рисунке.
Дополнительным элементом этой схемы является теплообменник (ТО), в котором
выходящие из турбины газы передают часть своей теплоты воздуху,
поступающему в теплообменник из компрессора.
Подогрев воздуха в теплообменнике уменьшает потребное количество теплоты,
подводимое к воздуху в камере сгорания, необходимое для обеспечения заданной
максимальной температуры цикла Tz.

25.

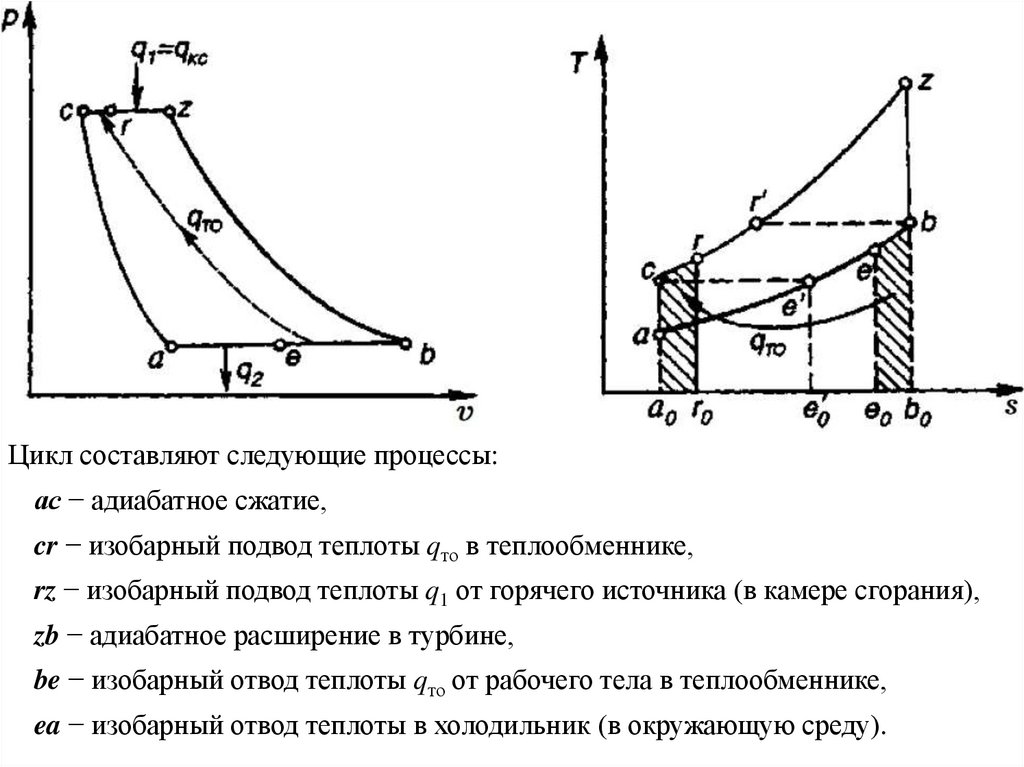
Цикл составляют следующие процессы:
ас − адиабатное сжатие,
cr − изобарный подвод теплоты qто в теплообменнике,
rz − изобарный подвод теплоты q1 от горячего источника (в камере сгорания),
zb − адиабатное расширение в турбине,
be − изобарный отвод теплоты qто от рабочего тела в теплообменнике,
ea − изобарный отвод теплоты в холодильник (в окружающую среду).

26.

Отношение величины действительного повышения температуры воздуха в
теплообменнике к максимально возможному называется степенью регенерации
Tr Tc
р
Tb Tc
(35)
Термический КПД рассматриваемого цикла равен
q2
t 1
q1
q1 − количество теплоты, подведённое к рабочему телу от горячего источника (в
камере сгорания);
q2 − количество теплоты отдаваемое рабочим телом холодильнику (в
окружающую среду)
q1 c p (Tz Tr )
q 2 c p (Te Ta ) c p (Tb Ta ) c p (Tb Te )
=c p (Tb Ta ) c p (Tr Tc )
t 1
c p (Tb Ta ) c p (Tr Tc )
c p (Tz Tr )

27.

Полагая, что cp не зависит от температуры и учитывая, что в соответствии с (35)
Tr = Tc + р(Tb Tc), после преобразований получаем
Tz Tb Tc
Ta 1
Ta Ta Ta
Tz Tb Tc Ta
t
Tz Tc р (Tz Tc )
Tz Tc
Tz Tc
Ta р
Ta Ta
Ta Ta
Оставляя отношение известных (задаваемых) температур Tz/Ta = и заменяя
остальные отношения температур их выражениями, полученными при
рассмотрении цикла без регенерации теплоты, приводим это уравнение к виду
(кk 1) k 1
(кk 1) k
t
( k 1) k
( k 1) k
к
р (k 1) k к
к

28.

1
t 1 (k 1) k
к
(кk 1) k
1 р (k 1) k 1
к
р
( k 1) k
к
(36)
При р= 0 из (36) получается уравнение t цикла ГТД без регенерации теплоты
t 1
1
(кk 1) k
Преобразование выражений удельной работы цикла с регенерации теплоты
l ц c p (Tz Tr ) c p (Tb Ta )
l ц q1 t
приводит к тому же выражению (31), что и в цикле без регенерации теплоты.
Следовательно, применение теплообменника в термодинамическом цикле на
удельную работу не влияет.
В действительном цикле вследствие гидравлических сопротивлений воздушных и
газовых каналов теплообменника и соответствующего падения давления в них
удельная работа несколько снижается.