Similar presentations:
Оптимизация природопользования
1.
Сысуев В.В.доктор географических наук, профессор
ОПТИМИЗАЦИЯ
ПРИРОДОПОЛЬЗОВАНИЯ
Введение в теорию оптимизации
Географический факультет
Московского государственного университета им. М.В.Ломоносова
v.v.syss@mail.ru
Москва, 2016
2.
Введение в учение о природно-антропогенныхландшафтах
[Николаев, и др., 2008, с. 7]
Основаниями классификации (выделения) природноантропогенных ландшафтов являются три критерия:
«…а)
степень антропогенной трансформации природных
ландшафтов…; б) наличие или отсутствие антропогенной
регуляции; в) социально-экономические функции, выполняемые
ландшафтами».
В соответствии с основными видами природопользования среди
природно-антропогенных обоснованно выделяются ландшафты:
«…целенаправленно созданные, антропогенно регулируемые:
1) сельскохозяйственные, 2) лесохозяйственные,
3) водохозяйственные, 4) городские и другие селитебные,
5)…»
3.
«…для перехода земной цивилизации к устойчивомуразвитию необходимо решить две взаимосвязанные
ландшафтно-экологические задачи планетарного масштаба.
Первая состоит в оптимизации всех существующих
природно-антропогенных ландшафтов с целью
преобразования их в истинно культурные (ноосферные).
Вторая – в сбережении, уходе и восстановлении естественных
природных комплексов, наиболее надежно гарантирующих
относительную стабильность природной среды за счет
гомеостазиса…
Важнейшим инструментом проектирования
культурного ландшафта признано ландшафтное
планирование. Его суть в научном обеспечении
оптимальной природно-хозяйственной организации
ландшафтного пространства на принципах геоэкологической
адаптивности»
[Николаев, 2013, с. 284].
4.
I. ОБ ОПТИМИЗАЦИИ ПРИРОДНО-АНТРОПОГЕННЫХ ЛАНДШАФТОВ«Проектирование - это начало изменений в
окружающей человека искусственной среде»
Дж. К. Джонс
Планирование, проектирование и управление
устойчивым природопользованием и задачи условной
оптимизации предполагают наличие одинаковых
предпосылок: имеется цель, которую нужно достичь,
учитывая всевозможные ограничения.
Мощный аппарат решения этих проблем имеет теория
оптимизации (оптимального управления).
Выражения, связывающее цель со средствами ее
достижения: критерий функционирования, критерий или показатель
эффективности, целевая или критериальная функция, функция цели
5.
Логический пример оптимизация:настраивая радиоприемник, мы добиваемся максимальной
громкости некоторой радиостанции:
Допустимой областью Х является
интервал углов поворота ручки настройки
между начальными н и конечными
значениями к. Целевая функция —
зависимость громкости F от угла . Путем
измерений получим значения целевой
функции F( ) и начертим ее график. Из
графика видно, что наибольшему значению
целевой функции соответствует
оптимальный угол ( опт). Математическое
выражение (или алгоритм вычисления)
целевой функции F( ), график которой
хорошо совпадает с экспериментальной
кривой, и называют математической
моделью.
Оптимизация - нахождение max (min) целевой функции
6.
Если множество всех вариантов Х, а его элементы – x, тосопоставив каждому варианту x из множества Х (x Х) число
— критерий оптимальности, получим функцию F(x),
определенную в области Х. Эта функцию, показывающая
«качество» выбираемых вариантов, целевая функция, а
область Х — допустимая область
Задача оптимизации - поиск минимума целевой функции:
F(x)→ min
x Х
7.
Для решения задач оптимизации необходимо:А) Составить математическую модель объекта
оптимизации
Б) Выбрать критерий оптимальности и составить
целевую функцию F(X)
В) Установить возможные ограничения, которые
должны накладываться на переменные
Г) Выбрать метод оптимизации, который позволит
найти экстремальные значения искомых величин
8.
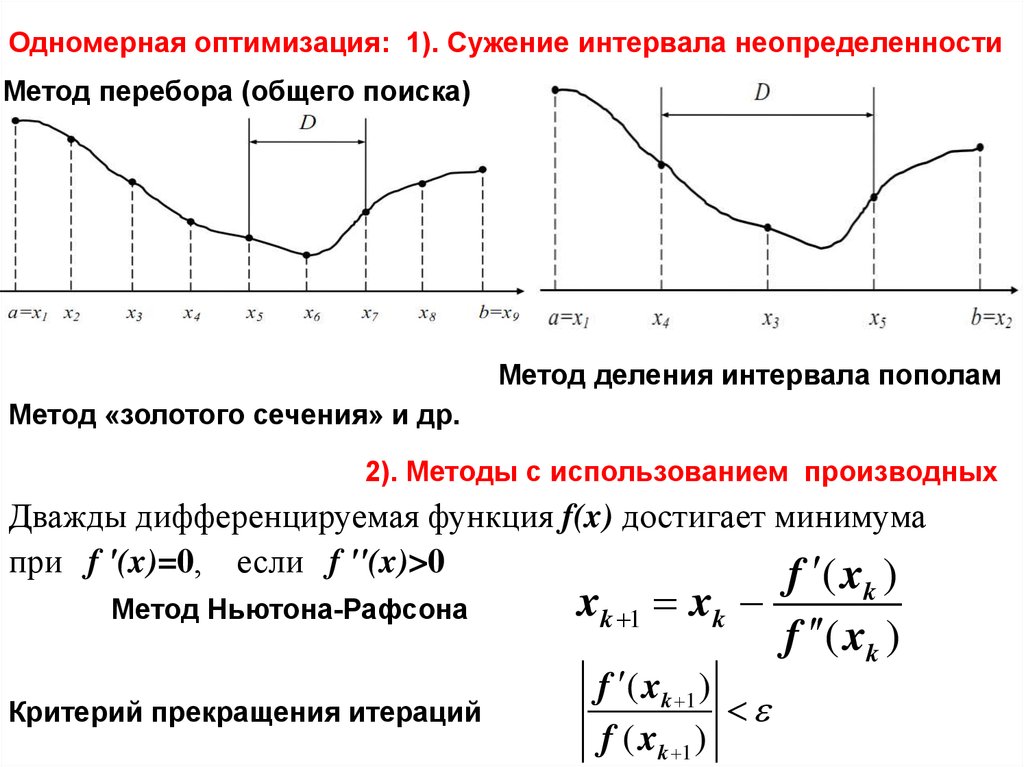
Одномерная оптимизация: 1). Сужение интервала неопределенностиМетод перебора (общего поиска)
Метод деления интервала пополам
Метод «золотого сечения» и др.
2). Методы с использованием производных
Дважды дифференцируемая функция f(x) достигает минимума
при f '(x)=0, если f ''(x)>0
f ( x )
Метод Ньютона-Рафсона
Критерий прекращения итераций
xk 1 xk
f ( xk 1 )
f ( xk 1 )
k
f ( xk )
9.
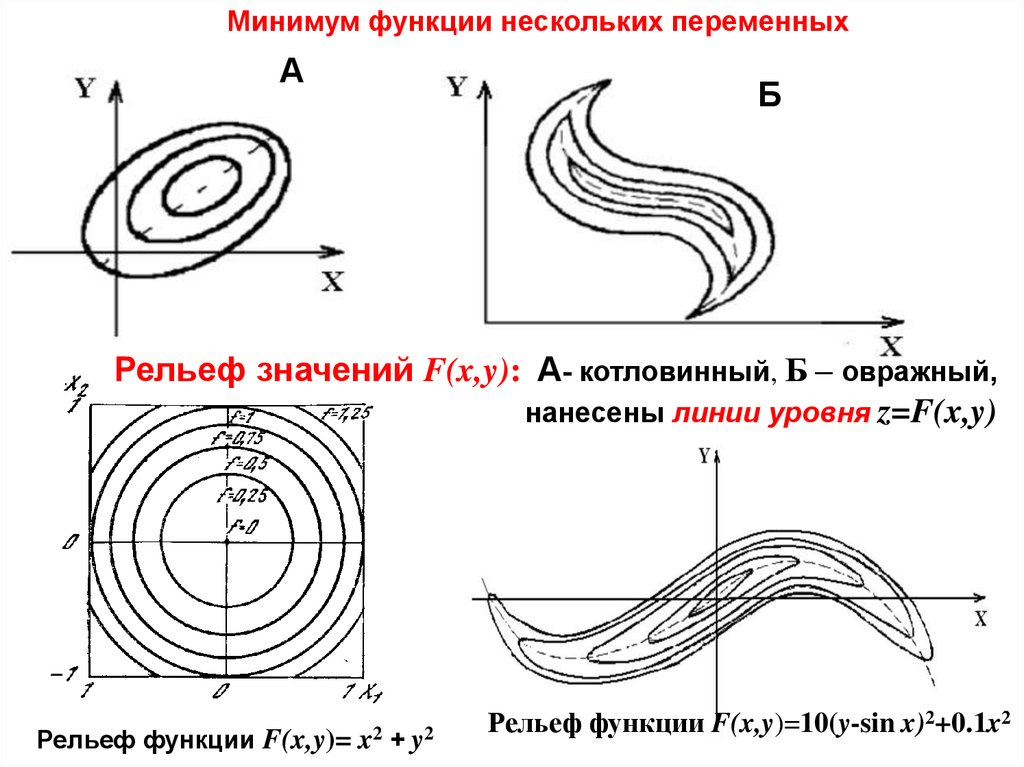
Минимум функции нескольких переменныхА
Б
Рельеф значений F(x,y): А- котловинный, Б – овражный,
нанесены линии уровня z=F(x,y)
Рельеф функции F(x,y)=
x2
+
y2
Рельеф функции F(x,y)=10(y-sin x)2+0.1x2
10.
Метод координатного спуска (метод Гаусса)F(x,y,z) - функция 3-х переменных. Пусть нулевое приближение x0 , y0 , z0 .
1. Фиксируем значение двух координат y= y0 , z=z0 . Функция f1= F(x,y0,z0)
только одной переменной – отыщем ее минимум и обозначим его x1.
т.е. сделали шаг из т. (x0 , y0 , z0) в т. (x1, y0, z0), и значение F(x,y,z)
уменьшилось
2. Из новой точки сделаем спуск по оси y, т.е. найдем минимум f2= F(x1, y, z0)
→
попадем в точку (x1, y1 , z0)
3. Третий шаг – спуск по оси z из т. (x1, y1 , z0) в т. (x1, y1 , z1) – цикл или первая
итерация завершена
11.
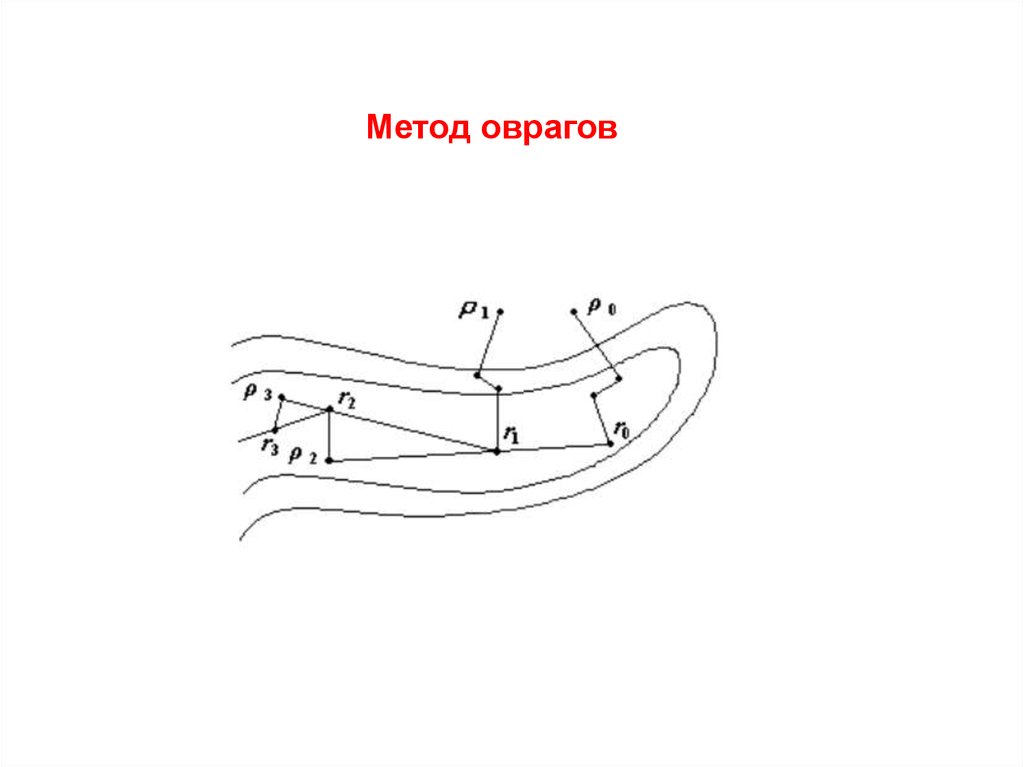
Метод оврагов12.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ [Канторович, 1939]1. Задача об использовании сырья
Виды
сырья
Запасы
сырья
S1
S2
S3
S4
b1
b2
b3
b4
Доход
Виды
продукции
П1
a11
a21
a31
a41
c1
П2
a12
a22
a32
a42
c2
Виды
сырья
S1
S2
S3
S4
Запасы
сырья
19
13
15
18
Доход
Виды
прордукции
П1
2
2
0
3
7
П2
3
1
3
0
5
Если предприятие выпускает х1 единиц продукции вида П1 и x2 единиц вида П2
2 x1 3 x2 19
2 x x 13
1
2
3
x
15
2
3 x1 18
F 7 x1 5 x2
0 19 2 x1 3 x2
0 13 2 x x
1
2
0
15
3
x
2
0 18 3 x1
х3 19 2 x1 3 x2
х 13 2 x x
4
1
2
х5 15 3 x2
х6 18 3 x1
F -7 x 5 x
Найти min
1
2
основная задача линейного программирования
13.
Геометрический смысл основной задачи линейногопрограммирования
Требуя неотрицательности всех неизвестных
приходим к системе
многоугольник решений
неравенств
системы неравенств
x1 0
x 0
2
19 2 x1 3 x2 0
13 2 x1 x2 0
15 3 x2 0
18 3 x1 0
F -7 x1 5 x2
P0 x1(0) , x2(0)
(I)
x1 0
C0 7 x1(0) 5 x2(0)
x 0
(II)
2
Оптимальная точка Q(5, 3)
19 2 x1 3 x2 0 (III)
F1min 7 5 5 3 50
13
2
x
x
0
(IV)
1
2
15 3 x2 0
(V) Оптимальное решение задачи:
x1= 5, x2 = 3.
(VI)
18 3 x1 0
C -7 x1 5 x2
14.
ЛИНЕЙНОЕ ПРОГРАММИРОВАНИЕ2. Транспортная задача
Пункты
отправления
A1
A2
Потребность
в грузе
Пункты
отправления
A1
A2
Потребность
в грузе
Пункты
назначения
Запасы
груза
B1 B2 B3
c11 c12 c13
a1
c21 c22 c23
a2
b1 b2 b3 ∑ai =∑bj
Пункты
назначения
B1 B2 B3
x11 x12 x13
x21 x22 x23
b1 b2 b3
Запасы
груза
a1
a2
∑ai =∑bj
а1, a2 - ед. груза на станциях отправления,
b1, b2, b3 груза на станциях назначения,
сij - стоимость перевозки единицы груза
xij количество ед. груза, предназначенного
к отправке
ОСНОВНАЯ ЗАДАЧА ОПТИМИЗАЦИИ
x11 x21 b1
x12 x22 b2
x13 x23 b3
x x x a
12
13
1
11
x21 x22 x23 a2
2
3
F c11 x11 c12 x12 c13 x13 c21 x21 c22 x22 c23 x23 cij xij cij xij
i 1 j 1
i, j
15.
Численный пример транспортной задачиМногоугольник решений
Пункты
отправления
Пункты назначения
Запасы
груза
B1
B2
B3
A1
x11
x12
x13
20=a1
A2
x21
x22
x23
30=a2
10=b1
30=b2
10=b3
∑ai =∑bj
Потребность
в грузе
(I)
20 x11 x12 0
10 x 0
(II)
11
30 x12 0
(III)
10 x11 x12 0 (IV)
x11 0
(V)
(VI)
x12 0
F 330 2 x11 x12
Оптимальное решение в точке N(10, 10)
x11 = 10, x12 =
10,
Fmin = 300.
x13 20 x11 x12 0
x 10 x 0
21
11
x22 30 x12 20
x23 10 x11 x12 10
16.
Задача рационального распределения пород деревьевпо соответствующим им ТУМ [].
Основная задача линейного программирования
Найти максимум целевой функции
n
F ( x ) c j ( ) x j max
при условиях:
j 1
ограничения на имеющиеся
природные ресурсы
выполнения предъявляемых
к насаждениям требований
и неотрицательности переменных:
(1)
n
a
j 1
pj
n
a
j 1
kj
( ) x j bp ( )
(2)
( ) x j bk ( )
сj( ) – запас, прирост или другая специфическая функция j-ой породы
в возрасте количественной спелости;
xj – доля участия j-ой породы в данных ТУМ xj 0, j = 1,..., n,
apj( ) – норма потребности j-ой породы в p-ом ресурсе;
bp( ) – количество имеющихся p-ых ресурсов;
akj( ) – нормы требуемых от насаждения дополнительных специфических
функций (средообразующих, биоразнообразия, защитных и др);
bk( ) – оценки требований к этим функциям;
- количество выделов.
17.
Географические ограничения по ресурсам в задачахоптимизации продукционных процессов
[Нестеров, Бредихин, 1970 ]
№ Наименование
Номера районов
1
2
3
4
1
Солнечная радиация,
ккал/см2 вегет. период
60
65
80
90
2
Доступная вода,
сотни тонн/га
340
300
250
115
3
Азот, кг/га
54
60
100
50
4
Фосфор, кг/га
12
15
27
16
5
Калий, кг/га
50
54
60
60
6
Почвы
7
∑to
2150
2200
2750
3000
8
pH
5,2
5,5
6,3
7,5
дерноводерновочернозем Темнокаш
подзолист. подзолист выщелоч. тановая
супесчаная среднесугл легкосугл среднесугл
18.
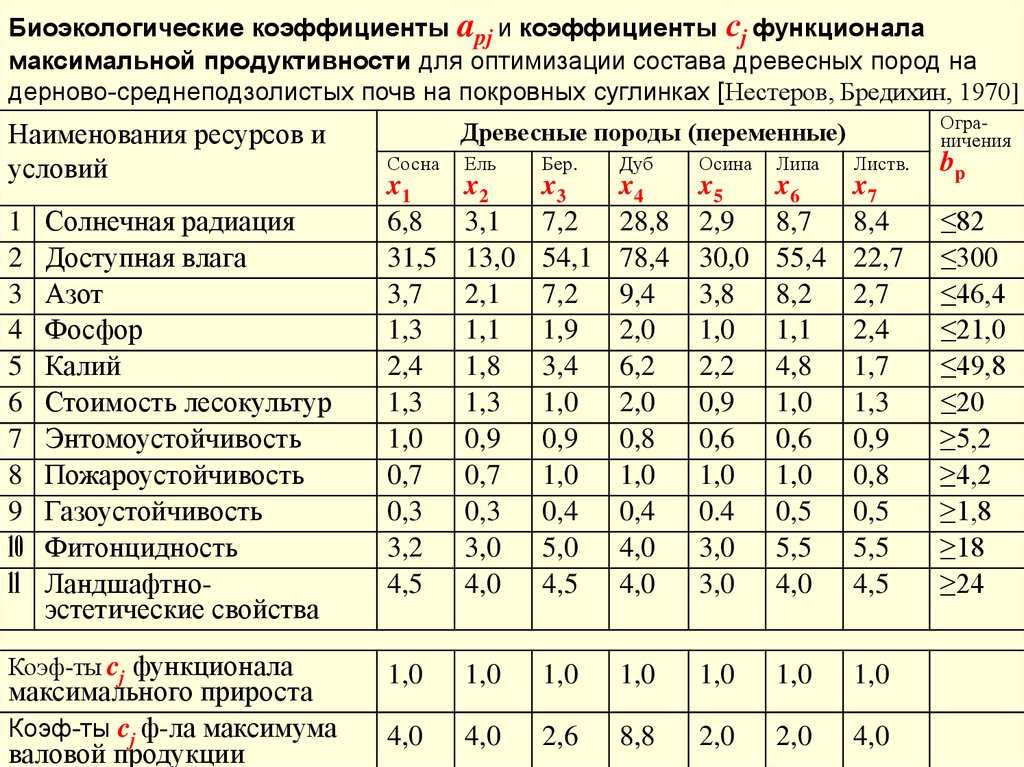
Биоэкологические коэффициенты apj и коэффициенты сj функционаламаксимальной продуктивности для оптимизации состава древесных пород на
дерново-среднеподзолистых почв на покровных суглинках [Нестеров, Бредихин, 1970]
Наименования ресурсов и
условий
1
2
3
4
5
6
7
8
9
10
11
Солнечная радиация
Доступная влага
Азот
Фосфор
Калий
Стоимость лесокультур
Энтомоустойчивость
Пожароустойчивость
Газоустойчивость
Фитонцидность
Ландшафтноэстетические свойства
Коэф-ты cj функционала
максимального прироста
Коэф-ты cj ф-ла максимума
валовой продукции
Ограничения
Древесные породы (переменные)
Сосна
x1
6,8
31,5
3,7
1,3
2,4
1,3
1,0
0,7
0,3
3,2
4,5
Ель
x2
3,1
13,0
2,1
1,1
1,8
1,3
0,9
0,7
0,3
3,0
4,0
Бер.
x3
7,2
54,1
7,2
1,9
3,4
1,0
0,9
1,0
0,4
5,0
4,5
Дуб
x4
28,8
78,4
9,4
2,0
6,2
2,0
0,8
1,0
0,4
4,0
4,0
Осина
x5
2,9
30,0
3,8
1,0
2,2
0,9
0,6
1,0
0.4
3,0
3,0
Липа
x6
8,7
55,4
8,2
1,1
4,8
1,0
0,6
1,0
0,5
5,5
4,0
Листв.
x7
8,4
22,7
2,7
2,4
1,7
1,3
0,9
0,8
0,5
5,5
4,5
1,0
1,0
1,0
1,0
1,0
1,0
1,0
4,0
4,0
2,6
8,8
2,0
2,0
4,0
bp
≤82
≤300
≤46,4
≤21,0
≤49,8
≤20
≥5,2
≥4,2
≥1,8
≥18
≥24
19.
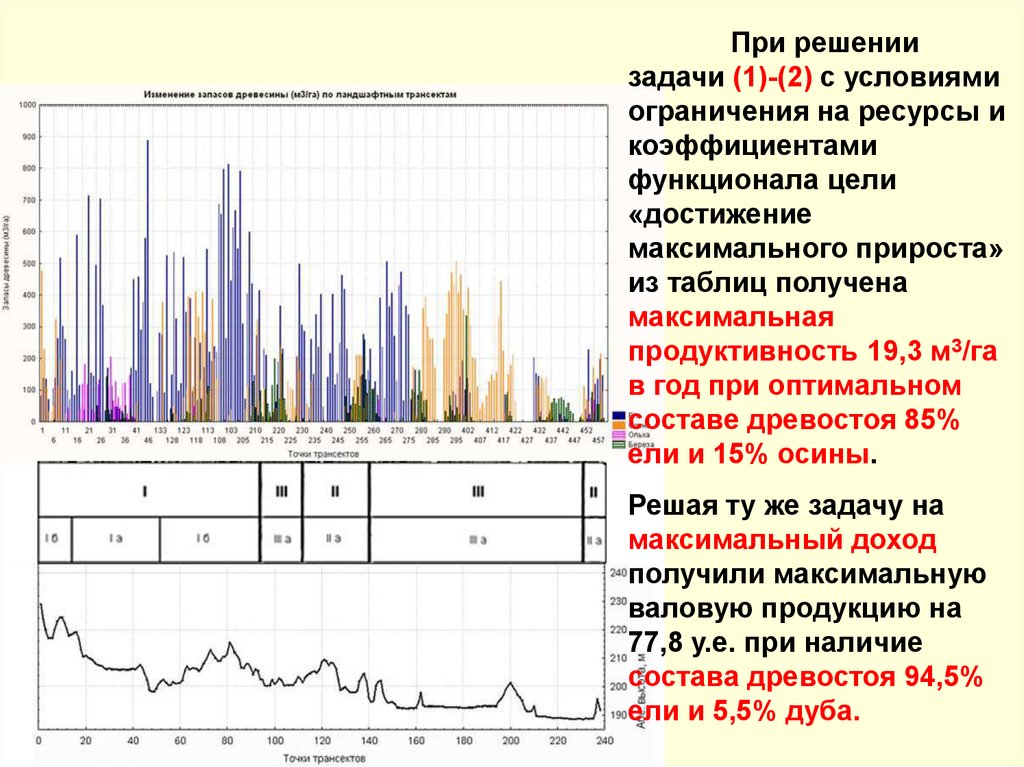
При решениизадачи (1)-(2) с условиями
ограничения на ресурсы и
коэффициентами
функционала цели
«достижение
максимального прироста»
из таблиц получена
максимальная
продуктивность 19,3 м3/га
в год при оптимальном
составе древостоя 85%
ели и 15% осины.
Решая ту же задачу на
максимальный доход
получили максимальную
валовую продукцию на
77,8 у.е. при наличие
состава древостоя 94,5%
ели и 5,5% дуба.
20.
Оптимизация лесопользования [В.Г. Нестеров, М.А. Бредихин, 1971].Основнаязадача линейного программирования в вероятностной постановке
Найти максимум математического ожидания целевой функции
n ln
M c ks ( ) xks max неотрицательных переменных xks 0, k , K , s, S;
k 1 s 1
C (ω) - чистый доход с дисконтированием затрат с помощью нормы эффективности вложений:
ks
Dtks( ) - доход от реализации s-го варианта в k-м участке в t году;
Tks
Tks
Ztks( ) - затраты на проведение s-го варианта в k-м участке в t-м году;
Dkst
Z kst
E - норма эффективности вложений; u - год, к которому приводится
cks ( )
t u
t u
значение показателя; t - рассматриваемый год; Tks - время, в течение
t u (1 E )
t u (1 E )
которого будет получен эффект от проведения s-го варианта в k-м
участке.
Условия ограничения:
1. По удовлетворению потребностей экономики
в лесной продукции
2. По распределению лимитированных ресурсов
n ln
P arks ( ) xks br ( ) ar , r , R;
k 1 s 1
n ln
P aiks ( ) xks Li ( ) ai , i , I i ;
k ln1 s 1
P aiks ( ) xks bik ( ) ai , i , I I1, k , K ;
хks - доля использования s-го варианта в k-м участке; s 1
3. По использованию других ресурсов
где:
arks( ) - объем получения r-го вида лесной продукции в k-м участке при s-м варианте;
br( ) - потребности экономики в r-м виде лесной продукции;
aiks( )- норма затрат i-го ресурса на проведение s-го варианта в k-м участке;
Li( ) - объем i-го вида лимитированных ресурсов;
bik( ) - объем i-го вида ресурсов в k-м участке;
I - множество всех ресурсов;
I1 - множество лимитированных ресурсов;
R - множество видов лесной продукции;
ar, ai - заданные вероятности соблюдения ограничений по удовлетворению потребностей и наличию ресурсов;
cks( ) - чистый доход от проведения s-го варианта в k-м участке.
21.
2. Задачи оптимального управленияприродопользованием
Система, точнее - динамическая система (которая развивается,
эволюционирует во времени) в каждый момент времени пребывает в
одном из некоторого числа возможных состояний.
Смена состояний системы с течением времени и составляет её
развитие или функционирование.
Предполагается, что состояние динамической системы в каждый
момент времени может быть однозначно охарактеризовано
определенным конечным набором n числовых параметров или
функций состояния.
Управление – это есть воздействие, способное изменить
текущее состояние, а значит и все последующее развитие системы.
Функционированием многих природно-антропогенных систем
можно (необходимо) управлять.
22.
Постановка задачи оптимального управления включает:1. Систему дифференциальных уравнений, описывающих
поведение (функционирование) данного объекта и
2. Критерий оптимальности (функционал), который следует
максимизировать или минимизировать,
3. Выбор управляющих переменных.
4. Введение ограничений на переменные и граничные условия
5. Формулировка принципа максимума Л.С. Понтрягина. Этот
принцип - необходимое условие существования оптимального
управления динамическими системами, принимает разный вид в
зависимости от задачи. В его формулировке участвуют функции
специального вида – гамильтониан и сопряженные переменные.
Существует схема применения принципа максимума, в общем случае
его использование требует высокой математической квалификации.
Решением задачи оптимального управления является
оптимальный процесс, т.е. оптимальное управление и
соответствующая ему оптимальная траектория функционирования
системы.
23.
Оптимальное управление лесопользованием. Простейшая модельV – мощность лесоперерабатывающего предприятия,
R – запас леса на выделенной территории. Доля доходов
тратится на рост производства; темп этого роста
с начальными условиями уменьшается с уменьшением запаса леса: a–g/R, а –
максимальный темп роста производственной мощности
при неограниченном запасе леса R=∞, g – некоторая
константа зависимости от ресурса. cV - интенсивность
потребления леса, которая значительно превосходит
естественную скорость лесовосстановления
(Решение сплошные линии)
Если запас R0 достаточно велик, так что
При затрате доли средств, на
лесовосстановление, снижается рост
производства на величину u. Скорость
восстановления леса считаем
пропорциональной u с
коэффициентом α (эффективность
затрат). Если u удастся задать так, что
запас стабилизируется
на
некотором уровне Rс тогда:
Решение – пунктирные линии
24.
Оптимальное управление вырубкой плакорных пихтовых лесовПриангарья
Si, площади занятые i –м типом леса; ji - ji
Si ji S j ij Si ui uNi uvi u pi интенсивность перехода из j-го состояния в i-е
j
j
состояние (тип леса), определяется по времени
- jiнеобходимому для смены типа леса; ui, uNi –
Оптимальное управление рубками:
интенсивность изменения площади вырубки и
S AS Bu DSV LSuv ,
потери лесных площадей в результате
V uv ,
пожаров; uv, up – потери лесной площади на
V 0 V0 , S 0 S0 , S t 0 ,
расширение мощности предприятия и
0 ui wi V , uv 0 ,
инфраструктуры
T
i
I1 u buv cV S S
0
2
V - мощность лесозаготовительного
dt max . предприятия, v - выпуск продукции,
ui – площадь, вырубаемая в каждом
типе леса. стоимости древостоев,
вырубаемых с площади u, входят
потери прибыли на увеличение
мощности предприятия uv и на
штрафы за нарушение экологических
условий (равновесия) S S 2
1
25.
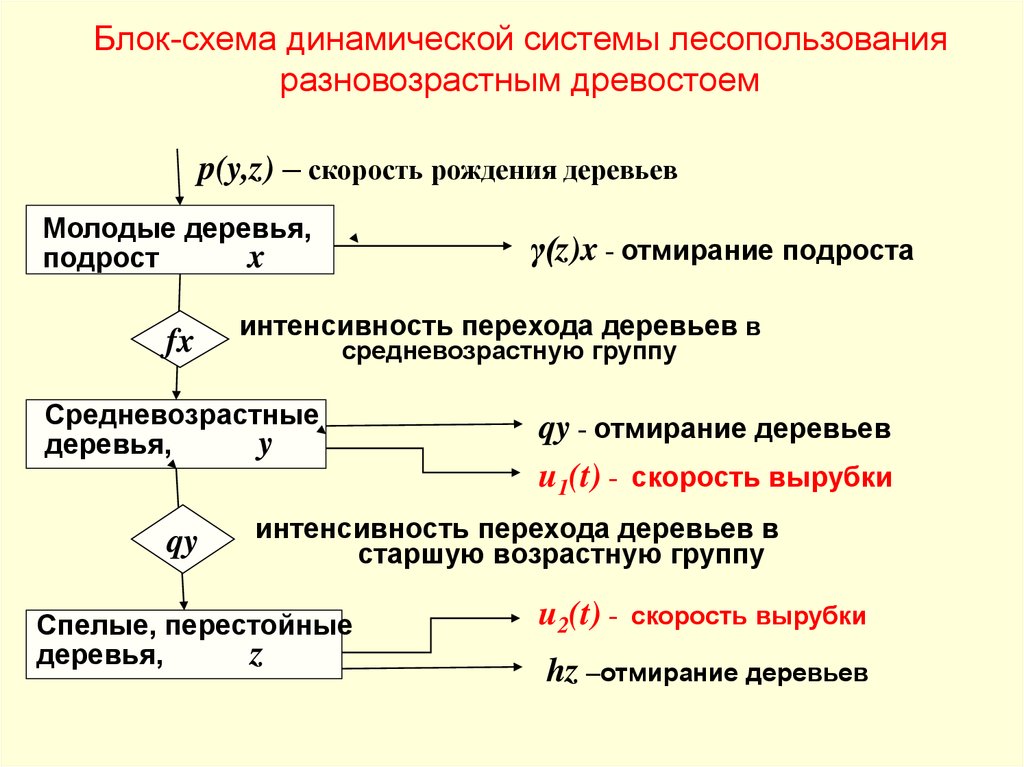
Блок-схема динамической системы лесопользованияразновозрастным древостоем
p(y,z) – скорость рождения деревьев
Молодые деревья,
подрост
x
fx
γ(z)x - отмирание подроста
интенсивность перехода деревьев в
средневозрастную группу
Средневозрастные
деревья,
y
qy
qy - отмирание деревьев
u1(t) - скорость вырубки
интенсивность перехода деревьев в
старшую возрастную группу
Спелые, перестойные
деревья,
z
u2(t) -
скорость вырубки
hz –отмирание деревьев
26.
Постановка задачи оптимального управления лесопользованием[Андреева, Шилова, 2014]
x p y, z z x fx ,
y fx q d y u1 ,
z qy hz u2 ,
с краевыми условиями:
x 0 X 0 , y 0 Y0 , z 0 Z 0 ;
x T X T , y T YT , z T ZT .
Функции управления u1(t), u2(t) - скорость вырубки деревьев
среднего и старшего возрастов: 0 uk t k , k 1,2 , t 0, T
2
0 uk t k ,
k 1
t 0,T ,
;
Цель управления - максимизация функционала J(u) - прибыль,
полученную от продажи вырубленного леса:
T
3
J u i y, z ci y, z ui dt b1 y T b2 z T max,
где: i
0 i 2
y, z ,
ci y, z -
стоимость реализованной древесины и
себестоимость затрат на выращивание и рубки
27.
Решение задачи оптимального управления лесопользованиемЗадача минимизации функционала с критериями выполнения конечных
T 3
условий:
J u i y, z ci y, z ui dt b1 y T b2 z T М1 max 0, X T x T
0 i 2
2
M 2 max 0,YT y T M 3 max 0, ZT z T min.
2
2
Строится функция Понтрягина из функций специального вида (гамильтониана
H и сопряженных переменных pi) и функция переключения
3
H t , x, y, z, u, p(t ), 0 0 i y, z ci y, z ui
i 2
p1 t , z z x fx p2 t , fx q d y u1 p3 t , qy hz u2 ;
k t k ck y, z pk 1 t , k 1,2.
Пусть x , y , z , u1 , u2 локально-оптимальный процесс
сформулированной задачи, тогда оптимальное
uk
управление определяется условием:
0, k t 0
k , k t 0
0, k , k t 0, k 2,3,
Сопряженные функции pk ,k=1,2,3 являются решением системы
дифференциальных уравнений: p t p t az 4 b f p
1
2 t f ;
p2 t 1u1 p2 t q d p3 t q;
p3 t 2 u2 p1 t 4az 3 x p3 t h
1





















 mathematics
mathematics geography
geography








