Методы оптимизации

1. Методы оптимизации

МЕТОДЫ
ОПТИМИЗАЦИИ
Лекция 7
Двойственность линейного
программирования
к.т.н., доцент
Кирпичёва Елена Юрьевна

2.

Исходная ЗЛП
Z c1 x1 c2 x2 ... cn xn
max
a11 x1 a12 x2 ... a1n xn b1 ,
.........................................
ak1 x1 ak 2 x2 ... akn xn bk ,
ak 11 x1 ak 12 x2 ... ak 1n xn bk 1 ,
...........................................
am1 x1 am 2 x2 ... amn xn bm ,
Двойственная ЗЛП
Z b1 y1 b2 y2 ... bm ym
a11 y1 a21 y 2 ... am1 y m c1 ,
..........................................
a1l y1 a2l y 2 ... aml y m cl ,
a1l 1 y1 a2l 1 y 2 ... aml 1 y m cl 1 ,
............................................
a1n y1 a2 n y 2 ... amn y m cn ,
yi 0
xj 0
m×n
m уравнений
n неизвестных
min
n×m
n уравнений
m неизвестных

3.

Правила построения двойственных задач:
1. Если в исходной задаче целевая функция
исследуется на min, то в двойственной задаче она будет
исследоваться на max и наоборот.
2. Если в исходной задаче n переменных и m
уравнений, то в двойственной задаче будет m переменных и
n уравнений.
3. Коэффициенты целевой функции исходной задачи
становятся правыми частями ограничений двойственной
задачи, а правые части системы ограничений исходной
задачи становятся коэффициентами целевой функции
двойственной задачи.

4.

Правила построения двойственных задач:
4. Матрица коэффициентов системы ограничений двойственной
задачи получается из матрицы коэффициентов системы
ограничений исходной задачи транспонированием.
5. Если в исходной задаче xk ≥ 0 то в двойственной задаче k-ое
ограничение будет неравенством, если же в исходной задаче xk не
имело ограничений на знак, то k-ое ограничение в двойственной
задаче будет равенством.
6. Если в исходной задаче l-ое ограничение - неравенство, то в
двойственной задаче yl ≥ 0, если же в исходной задаче l-ое
ограничение - равенство, то в двойственной задаче нет
ограничений на знак yl.

5.

Пример построения двойственной задачи
Исходная задача
Двойственная задача
3x 2 x 3x 5x min
1
2
3
4
2 x 4 x 5
1
4
3x 2 x 10
2
3
4 x 5 x 3x 7
1
2
4
2 y
4 y 3
1
3
3 y 5 y 2
2
3
2 y 3
2
3 y 5
4 y
1
3
x , x , x 0
1 2 3
A=
2
0
4
A
T
2
0
0
4
0
0
4
3
2
0
5
0
0
3
5
0
3
4
3
2
0
5 y 10 y 7 y max
1
2
3
y 0
1
y знака
2
y 0
3

6.

Связь между решениями прямой и
двойственной задач
Лемма 1
Если исходная задача (X) исследуется на max, а двойственная (Y) на min, то Z ( x) Z ( y )
Лемма 2
Если Z ( x * ) Z ' ( y * ) , то
x * , y * – оптимальные планы.
Теорема 1 (1 –ая теорема двойственности)
Если одна из пары двойственных задач имеет оптимальные планы, то и другая имеет
оптимальный план, причем : Zmax = Z’min.
Если же в одной из задач целевая функция не ограничена на ОДЗ, то у другой
задачи вообще нет допустимых планов.
Теорема 2 (2 –ая теорема двойственности)
План X*-исходной задачи и план Y*-двойственной
задачи являются оптимальными тогда и только
тогда, когда выполняется равенство:
m
*
aij yi c j x* 0,
j
i 1
j 1,...n

7.

Пара симметричных двойственных задач
Z с1x1 ... cn xn max
a x a2 x2 ... a1n xn b1
11 1
m1 1
......................................
a x am2 x2 ... amn xn bm
x 0( j 1,n)
j
Z ' b1 y1 ... bm ym min
a y a21 y2 ... am1 ym c1
11 1
1n 1
.........................................
a y a2n y2 ... amn ym cn
y 0(i 1,m)
i
Пары сопряженных переменных
Основные
Дополнительные
x1 , x2 ,..., xn ,
xn 1 , xn 2 ,..., xn m
y m 1 , y m 2 ,..., y m n ,
Дополнительные
y1 , y 2 ,..., y m
Основные

8.

Экономический смысл двойственных задач
Сырьё
№1
№2
Цена, руб
y , y , ≥ 0.
1 2
Расход сырья
(усл. ед.)
на 1 ед. товара
Товар А
Товар Б
1
3
2
1
3000
2000
Задача I (исходная)
Запасы сырья
6
8
Задача II (двойственная)
Z = 3000·x1 + 2000·x2 → max
Z’ = 6·y1 + 8·y2 → min
Переменные двойственной задачи (двойственные оценки)
x1 3x2 6
2 x1 x2 8
x1 0, x2 0
y1 2 y 2 3000
=
Теневые цены 3 y1 y 2 2000
y1 , y 2 0

9.

Экономический смысл двойственных задач
Т.к. по первой теореме двойственности Zmax = Z’min, то
предприятию безразлично, производить ли продукцию по оптимальному плану X*
и получить от ее реализации прибыль в размере Zmax или начать продавать
ресурсы по оптимальной цене Y* и возместить от продажи равные ей
минимальные затраты на ресурсы Z’min:
Zmax = Z’min = b1·y1 + b2·y2
Можно определить как изменится прибыль от производства Zmax при
изменении объема i-го сырья.
Теневая цена будет показывать, на какую величину изменится максимальный доход Zmax при изменении запаса соответствующего сырья на единицу.

10.

Экономический смысл двойственных задач
Переменная двойственной задачи – это:
1) оценка (теневая цена), соответствующая одной единице ограниченного i-го
сырья.
2) равна величине, на которую могла бы увеличиться суммарная прибыль от
производства, если бы количество этого ограниченного сырья увеличилось на
единицу (если это увеличение было бы использовано оптимально).
3) количество прибыли, недополученной из-за нехватки единицы ограниченного
сырья bi.

11.

Экономический смысл двойственных задач
F 2 x1 3 x2 max
Z 18 y1 16 y2
x1 3 x2 18
2 x x 16
1 2
x2 5
3 x1 21
x1 , x2 0
F
*
5 y3 21 y4 min
y1 2 y2 3 y4 2
3 y1 y2 y3 3
y1 , y2 , y3 , y4 0
max
Z
*
min
24

12.

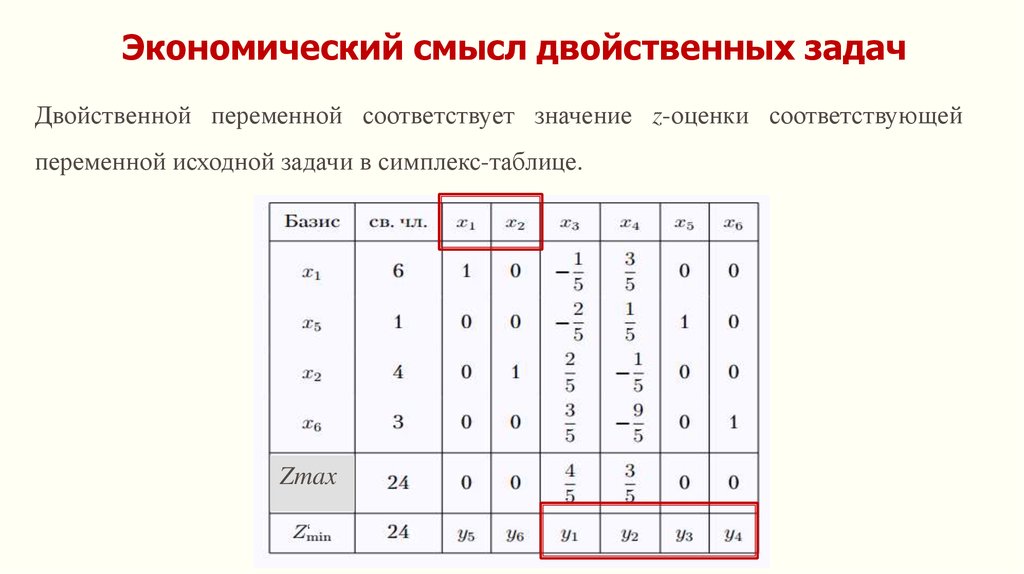
Экономический смысл двойственных задач
Двойственной переменной соответствует значение z-оценки соответствующей
переменной исходной задачи в симплекс-таблице.
Zmax
‘

13.

Экономический смысл двойственных задач
Задача 1
Остатки ресурсов
Число единиц
продукции
x*1 = 6
x*2 = 4
x*3 = 0
x*4 = 0 x*5 = 1 x*6 = 3
y*5 = 0
y*6 = 0 y*1 = 4/5 y*2 = 3/5 y*3 = 0 y*4 = 0
Превышение
затрат
на ресурсы
- дефицитные
ресурсы
получают ненулевые оценки, которые определяют степень их
Условные цены ресурсов
дефицитности;над ценой
реализации
- теневые цены (y*) показывают, на сколько денежных единиц изменится
Задачапродукции
2
максимальная выручка от реализации
при изменении запаса
соответствующего ресурса на одну единицу.

14.

Исследование на чувствительность
При исследовании на чувствительность исследуется зависимость решения
ЗЛП от небольших изменений коэффициентов в условии задачи. При этом
предыдущее решение может стать либо недопустимым, либо неоптимальным.
К недопустимости пред. решения могут привести изменения запасов ресурсов
и/или добавление новых ограничений.
К неоптимальности пред. решения могут привести изменение целевой
функции и/или изменение технологических коэффициентов и/или включение
в модель нового вида производственной деятельности.
Исследование на устойчивость
Исследование на устойчивость – исследование диапазона изменения правых
частей системы ограничений, при котором найденное оптимальное решение не
изменяется.