Similar presentations:
Составляющие постановки задачи оптимизации
1.
Список литературы1. Исследование операций в экономике: Учебное пособие для
вузов / Н.Ш. Кремер и др. – М.: Банки и биржи, ЮНИТИ,
1997. – 407 с.
2. Акулич И.Л. Математическое программирование в примерах
и задачах: Учебное пособие. – М.: Высш. шк., 1993. – 336 с.
3. Соловьев В.И. Методы оптимальных решений: Учебное
пособие. – М.: Финансовый университет, 2012. - 364 с.
2. Составляющие постановки задачи оптимизации
• Решение (план) задачи - вектор X [ x1 , x2 ,....xn ] .T
• Целевая функция (функция цели, показатель
эффективности) F X .
• Условия D (система ограничений), налагаемые на
компоненты вектора
X
.
3. Формальная постановка задачи оптимизации
определитьmin(max) F ( X )
X D
,
(1)
где
h ( X ) 0 , i 1,k
(2)
i
D:
j 1,l
g j ( X ) 0 ,
*
Допустимый план X , доставляющий функции цели
экстремальное значение
оптимальным.
(min
или
max),
называется
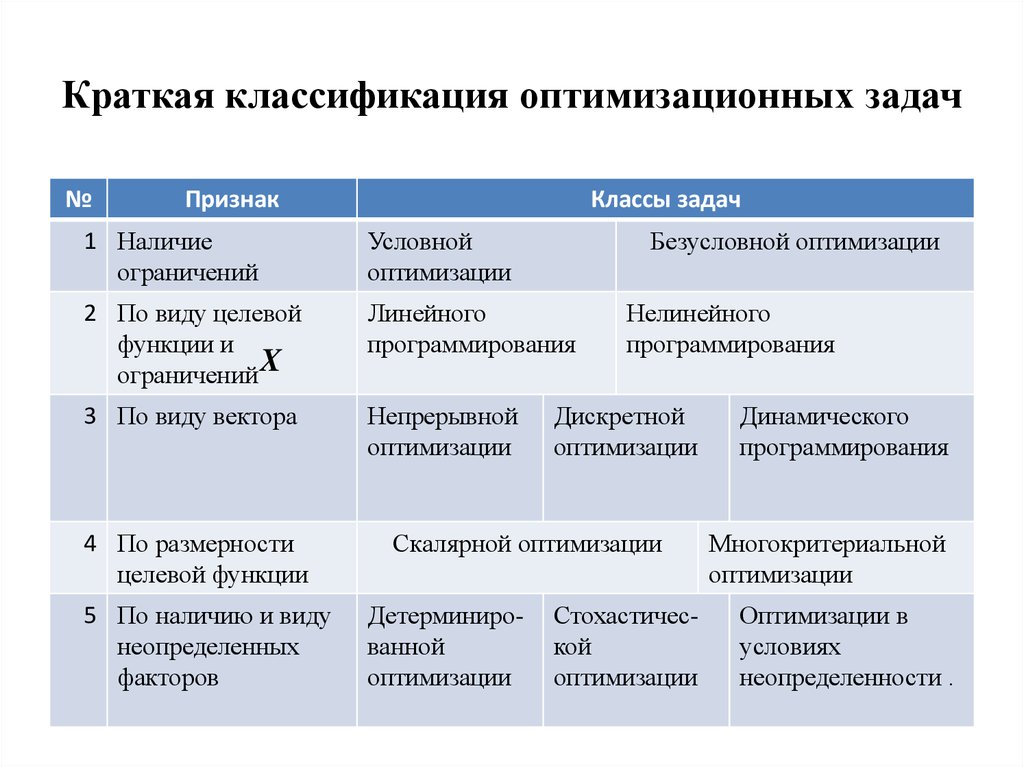
4. Краткая классификация оптимизационных задач
№Признак
Классы задач
1 Наличие
ограничений
Условной
оптимизации
2 По виду целевой
функции и
ограничений X
Линейного
программирования
3 По виду вектора
Непрерывной
оптимизации
4 По размерности
целевой функции
5 По наличию и виду
неопределенных
факторов
Безусловной оптимизации
Нелинейного
программирования
Дискретной
оптимизации
Скалярной оптимизации
Детерминированной
оптимизации
Стохастической
оптимизации
Динамического
программирования
Многокритериальной
оптимизации
Оптимизации в
условиях
неопределенности .
5. Задача линейного программирования (ЛП)
1. Общая задача ЛПn
определить
где
min ( max ) F ( X )
X D
cjxj
j 1
n
aij x j bi , i 1,k
j
1
n
D : aij x j bi , i (k 1) ,m
j 1
x 0,
j 1,l
j
(3)
(4)
6. Матричная форма общей задачи ЛП
определить min ( max ) F ( X )X D
где
C X,
A1 X B1
D : A2 X B2
j 1,l
x j 0,
T
(5)
(6)
7. В постановке (5), (6):
Tdim C 1 n
dim A1 k n
dim A2 s n
k s m;
l n.
dim X n 1
dim B1 k 1
dim B2 s 1
8. 2. Стандартная задача ЛП
определитьmin ( max ) F ( X )
X D
C X,
T
(7)
где
AX B
D:
X 0n
(8)
9. 3. Каноническая задача ЛП
определитьmin ( max ) F ( X )
X D
где
!!!
Замечание.
CT X ,
AX B
G:
X 0n
Любая
задача
(9)
(10)
ЛП
может
быть
представлена в виде канонической, стандартной или
общей задачи ЛП.
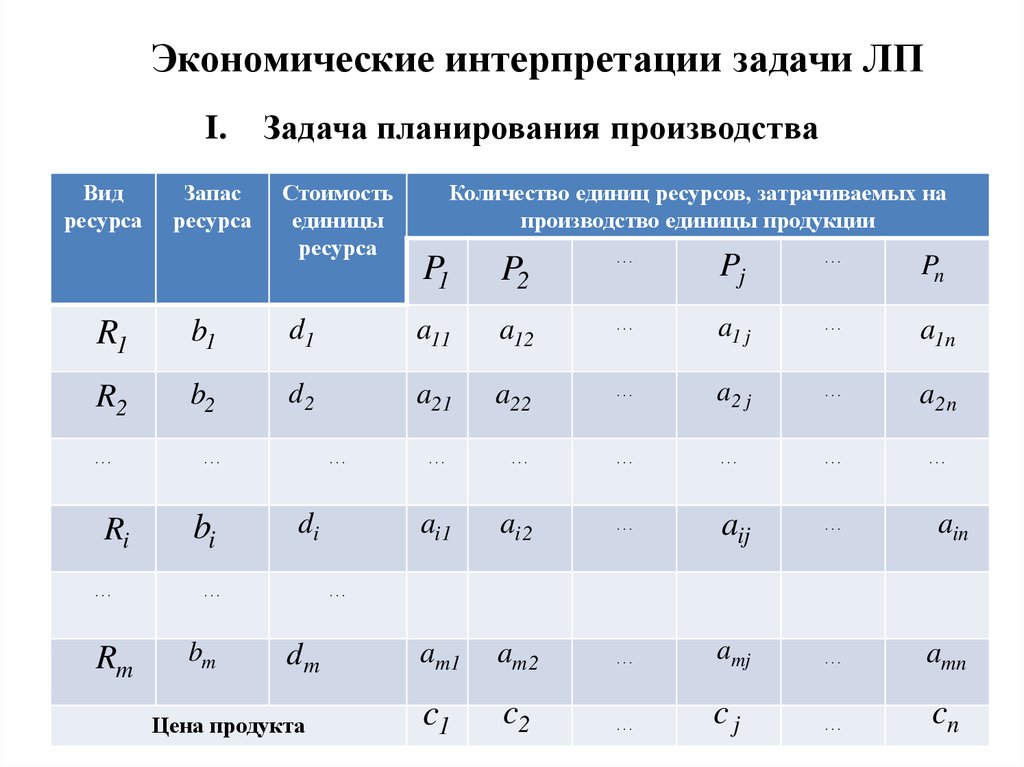
10. Экономические интерпретации задачи ЛП
I.Вид
ресурса
Запас
ресурса
Задача планирования производства
Стоимость
единицы
ресурса
Количество единиц ресурсов, затрачиваемых на
производство единицы продукции
P1
P2
…
Pj
…
Pn
R1
b1
d1
a11
a12
…
a1 j
…
a1n
R2
b2
d2
a21
a22
…
a2 j
…
a2n
…
…
…
…
…
…
ai1
ai2
…
aij
…
ain
am1
am2
…
amj
…
amn
c1
c2
…
cj
…
cn
…
Ri
…
Rm
…
bi
…
di
…
bm
…
dm
Цена продукта
11. Какое количество единиц каждого продукта необходимо произвести, чтобы получить максимальную прибыль?
Постановка задачи.T
1. План производства: X x1 , , xn
2. Ограничения.
• Физический смысл:
x j 0, j 1, n
(11)
;
• Условие ограниченного спроса:
x j k j , j 1, n;
(12)
• Ресурсов должно хватить:
n
aij x j bi
j 1
i 1,m
;
(13)
12. 3. Целевая функция: чистая прибыль от реализации всего плана производства
• Себестоимостьs j единицы продукции Pj :
m
s j di aij
i 1
j 1,n
• Чистая прибыль от реализации единицы продукции
qj cj sj
Pj :
j 1,n
• Чистая прибыль от реализации всего плана производства:
n
F X q j x j , j 1, n
j 1
(14)
13. Формальная постановка задачи планирования производства
Требуется определить план производства Xx1 ,
,
T
xn ,
обеспечивающий максимальное значение целевой функции
F X вида (14) при соблюдении ограничений на вектор X
вида (11), (12), (13).
Замечание. Постановка (11)-(14) является стандартной
задачей ЛП.
14. Транспортная задача (ТЗ)
II. Транспортная задача (ТЗ)Потребители
\\\\\\\\\\\\\\\
Источники
И1
…
Иi
П1
…
Пj
…
Пn
c11
…
c1 j
…
c1n
…
…
…
…
…
cij
ci1
…
Кол-во
ресурсов
a1
…
cin
ai
…
…
…
…
Иm
cm1
…
b1
…
Заявки на
товары от
потребителей
…
cmj
bj
…
…
…
cmn
…
bm
am
ai b j
i
j
15. II.1. ТЗ по критерию стоимости
Предполагаем, чтоcij - стоимость перевозки единицы ресурса И i со склада
в пункт потребления П j ;
ai b j
i
j
, т.е. ТЗ с правильным балансом.
Постановка задачи.
1. План производства:
T
X xij , i 1, m; j 1, n .
2. Ограничения.
• физический смысл:
xij 0, i 1, n; j 1, n .
(15)
16.
• Емкости складов д.б. израсходованы полностью:n
(16)
i 1, m .
xij ai
j 1
• Заявки, поданные потребителями, д.б. удовлетворены:
m
(17)
xij b j j 1, n .
i 1
3. Общая стоимость перевозок:
m n
F X cij xij .
i 1 j 1
(18)
17. Формальная постановка ТЗ по критерию стоимости
Требуется определить план перевозокX ,
обеспечивающий минимальное значение целевой функции
F X вида (18) при соблюдении ограничений на вектор
вида (15), (16), (17).
Замечание. Постановка (15)-(18) является канонической
задачей ЛП.
18. II.2. ТЗ по критерию времени
Предполагаем, что- время перевозки ресурса
cij xij
пункт потребления
со склада И i в
П j (зависит, вообще говоря, от
объема перевозки );
ai b j
i
, т.е. ТЗ с правильным балансом.
j
Постановка задачи.
1. План производства:
T
X xij , i 1, m; j 1, n .
2. Ограничения:– (15)-(17).
19.
3. Общее время всех перевозок T – все перевозкизаканчиваются, в момент, когда заканчивается самая
длительная из всех перевозок:
T F X max
i 1, m ,
j 1, n ,
xij 0
c x
ij
ij
(19)
20. Формальная постановка ТЗ по критерию времени
Требуется определить план перевозокX ,
обеспечивающий минимальное значение целевой функции
F X вида (19) при соблюдении ограничений на вектор
вида (15), (16), (17).
Замечание. Постановка (15), (16), (17), (19) является задачей
нелинейного программирования.
21. Пример 1.
Сформулировать постановку задачи планированияпроизводства в виде задачи ЛП.
Дана таблица.
Вид ресурса
Запас ресурса
Кол-во единиц ресурсов,
затрачиваемых на
изготовление единицы
продукта
P1
P2
S1
S2
S3
180
6
8
160
7
6
50
4
1
S4
210
3
2
22. Прибыль от реализации единицы продукции и составляет 20 и 30 тыс. рублей соответственно.
Прибыль от реализации единицы продукции P1 исоставляет 20 и 30 тыс. рублей соответственно.
P2
Требуется найти план производства продукции, при котором
Прибыль от ее реализации будет максимальной.
T
Решение.
X x1 , x2 - план производства продукции
P1 и P2 соответственно.
Для реализации плана производства X потребуется
ресурсов
S1 : 6 x1 8x2 ; S2 : 7 x1 6 x2 ;
S3 : 4x1 1x2 ; S4 : 3x1 2x2 .
23. Потребление ресурсов не должно превышать их запасы:
6 x1 8x2 1807 x1 6 x2 160
4x1 1x2 50
3x1 2x2 21
(20)
Исходя из физического смысла:
x1 0 , x2 0 .
(21)
Суммарная прибыль:
F X 20x1 30x2 max
(22)
24. Пример 2.
Привести стандартную задачу ЛП к канонической форме.F X x1 x2 max
2x1 x2 1
x1 x2 0
x1 0 , x2 0.
Решение. Введем новые переменные по правилу:
2x1 x2 1 x3
x1 x2 x4
25. Каноническая форма:
F X x1 x2 maxпри ограничениях
2x1 x2 x3 1
x1 x2 x4 0
x1 0 , x2 0 , x3 0 , x4 0.





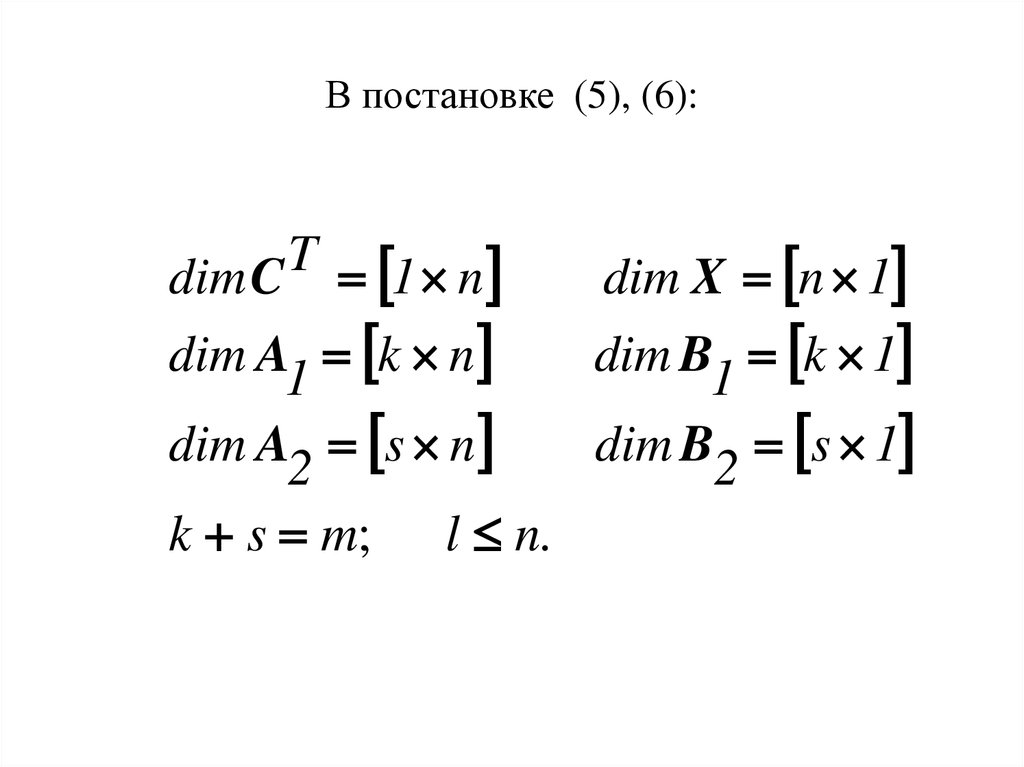

















 mathematics
mathematics








