Негиперболичность системы гидродинамических уравнений климатической модели атмосферы

1. НЕГИПЕРБОЛИЧНОСТЬ СИСТЕМЫ ГИДРОДИНАМИЧЕСКИХ УРАВНЕНИЙ КЛИМАТИЧЕСКОЙ МОДЕЛИ АТМОСФЕРЫ

Уравнения умнее тех, кто их вывел.
Генрих Герц (1857-1894)
НЕГИПЕРБОЛИЧНОСТЬ СИСТЕМЫ
ГИДРОДИНАМИЧЕСКИХ УРАВНЕНИЙ
КЛИМАТИЧЕСКОЙ МОДЕЛИ АТМОСФЕРЫ
Р.И. Нигматулин, Сюй Сюлинь
МОСКОВСКИЙ ГОСУДАРСТВЕННЫЙ
УНИВЕРСИТЕТ им. М.В. Ломоносова
РОССИЙСКАЯ АКАДЕМИЯ НАУК
Механико-математический факультет
Семинар В.А. Садовничего
11 декабря 2019 г.
МГУ им. В.М. Ломоносова
Институт океанологии
им П.П. Ширшова РАН

2.

Гидротермодинамические уравнения для
атмосферы
d
1 vx vy vz
− уравнение сохранения массы
dt
x y z
d
vx
vy
vz
dt t
x
y
z
dvx
p
xy
xz
f x(cor) xx
x
y
z
dt
x
p
- уравнения
f y(cor) -yxуравнения
yy yz
сохранения
импульсасохранения
импульса
dt
y
x
y
z
zx zy zz
dvz
p
(cor)
f z g
x
y
z
dt
z
dvy
1 d
1 dp 1 Q
dT Q
p d
− уравнение притока тепла
=
dt
p dt
p
dt cv cv dt
q
Q
Q J (е) l (е) J (m) l (m)
z
Уравнения состояния совершенного газа
p R T
u cv T const
cv R / ( 1)

3.

ДЛЯ ЗАМЫКАНИЯ СИСТЕМЫ УРАВНЕНИЯ
НЕОБХОДИМЫ УРАВНЕНИЯ:
- для вертикального теплового потока q
(турбулентная теплопроводность).
- для выделения тепла из-за поглощения
радиации Q, определяемого уравнениями для
потоков коротковолновой радиации G,
длинноволновой радиации U.
- для интенсивности испарения (конденсации) J(е),
плавления льда или снега) J(m),
и тепла J(е)l(е) + J(m)l(m) фазовых переходов.

4.

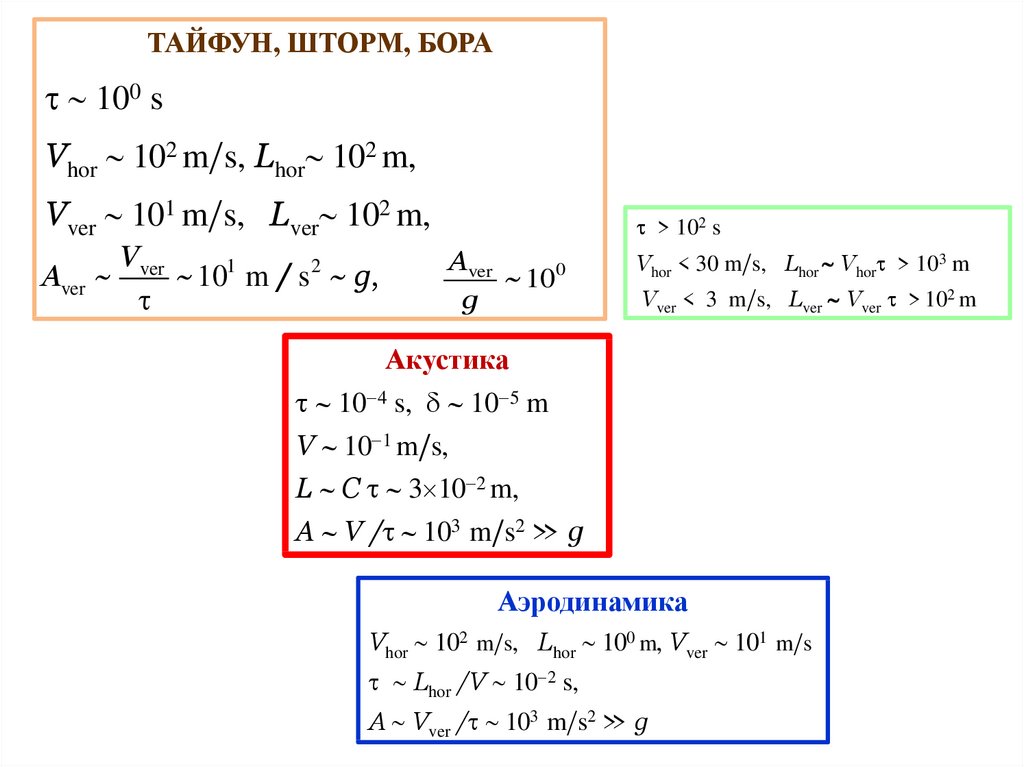
КЛИМАТИЧЕСКИЕ и МЕТЕОРОЛОГИЧЕСКИЕ
МАСШТАБЫ
100 s
> 102 s
103 m
Vhor 102 m/s, Lhor 102 m,
> 102 m
Vver 30 m/s, Lver 102 m,
Vhor < 30 m/s, Lhor Vhor >
Vver < 3 m/s, Lver Vver
ТАЙФУН, ШТОРМ,
БОРА
КЛИМАТ,
ПОГОДА
vx
t
~
vy
vх
x
vz
x
vz
t
Vhor
~
t
vx
~
y
vz
~
y
vх
~
y
Vver
~
Lhor
~
Vver
~
vy
Vhor
~
x
Lhor
vz
z
Vver
~
Lver

5.

t
x
y
z
t , x
, y
, z
,
Lhor
Lhor
Lver
vx
vx
vz
vx
, vy
, vz
О 1
Vhor
Vhor
Vver
dvx Vhor vx
vx
vx
vx
vx
vy
vz
dt
t
x
y
z
dvx
Ahor dt
AhorО 1
vy
vy
vy
dvy
Vhor vy
vx
vy
vz
Ahor
dt
t
x
y
z
dt
AhorО 1
dvz Vver vz
vz
vz
vz
v
v
v
x
y
z
dt
t
x
y
z
AverО 1
dvy
dvz
A
ver
dt
a (cor) f (cor) f (cor) 2 v 2Vcor e o v
2
24 час
0, 727 10 4 с 1,
Acor 2Vcor
~
Vhor
cor

6.

dvi
Безразмерные функции vi ,
О 1
dt
Масштабы ускорений
Ahor
2
Vhor Vhor
10 1 м / с 2 ,
Lhor
Aver
2
Vver Vver
10 2 м / с 2 ,
Lverr
Acor 2 Vhor 1, 4 10 3 м / с 2
Ahor Aver Acor
,
,
g
g
g
2
3
4
10 , 10 , 10
Ahor Aver Acor
,
,
g
g
g
> 102 s
Vhor < 30 m/s, Lhor Vhor > 103 m
Vver < 3 m/s, Lver Vver > 102 m
0

7.

ТАЙФУН, ШТОРМ, БОРА
100 s
Vhor 102 m/s, Lhor 102 m,
Vver 101 m/s, Lver 102 m,
V
Aver ~ ver ~ 101 m / s 2 ~ g,
> 102 s
Aver
~ 100
g
Vhor < 30 m/s, Lhor Vhor > 103 m
Vver < 3 m/s, Lver Vver > 102 m
Акустика
10 4 s, 10 5 m
V 10 1 m/s,
L C 3 10 2 m,
A V / 103 m/s2 >> g
Аэродинамика
Vhor 102 m/s, Lhor 100 m, Vver 101 m/s
Lhor /V 10 2 s,
A Vver / 103 m/s2 >> g

8.

УРАВНЕНИЯ МПУЛЬСА
p
dv
x ax(cor)
x
dt
p
dv
z az(cor)
g
z
dt
dv
p
y ay(cor)
y
dt
p
g 1 O
z
p
O Ahor Acor
y
p
O Ahor Acor
x
H
p t , x , y, z g dz g dz gM
0
z
H
p
M
g
g
dz
x 0 x
x
z
H
p
M
g
g
dz
y 0 y
y
z
H
M t , x , y, z t , x , y, z dz
z
z
Как рассчитать вертикальную скорость vz ?

9.

ВЕРТИКАЛЬНЫЕ ПОТОКИ. Дождь (фото с борта самолета)

10.

ВЕРТИКАЛЬНЫЕ ПОТОКИ. Образование грозы
(фото с борта самолета на высоте 11 000 м).

11.

УРАВНЕНИЕ СОХРАНЕНИЯ МАССЫ
vx vy vz
1 d
div v
dt
x y z
vx vy 1 d
vz
z
x y dt
Уравнение для распределения
вертикальной скорости
по вертикали

12.

ОКЕАН: 10 4 - 10 3
1 dT
1 d 1 dp 1 dS
vx vy vz
<<
+
+
,
,
T S ,T dt
dt p S ,T dt S p,T dt
x y z
vx vy 1 d
vz
z
x y dt
vy
v x
v z
- Квазинесжимаемость
z
x
y
Обыкновенное дифференциальное уравнение
для распределения вертикальной скорости
по вертикали в океане
Хотя океанские течения происходят именно из-за
переменности плотности: (p, T, S)

13.

Атмосфера: 100
1 d
1 dp 1
Q - уравнение притока тепла
dt
p dt
p
для совершенного газа
vx vy 1 d
vz
z
y dt
x
1 d
dt
vx vy 1 dp 1
vz
Q
z
x y p dt p
H
p t , x , y, z g dz Mg
z

14.

gM
H
v vy
dp p
p
p
p
x
vz
vx
vy
g
x
y
dt t
z
x
y
z
dz
p
p
vx
vy
y
x
vx vy 1 dp 1
vz
Q
z
x y p dt p H
O( )
p gM g t , x , y, z dz
z
v z
z
vx vy 1 M
1 Q
y M
gM
x
H
H
( vy )
M
M t , x , y, z dz , M ( vx )
vz
dz
x
y
t
z
z
M
(z ),
z
M ( vx ) ( vy )
z x
y

15.

Уравнения сохранения для атмосферы
с вертикальной квазистатикой (относительно , vx, vy)
t
1 M 1 Q
vx
vy
vz
t
x
y
z M
gМ
div v
vx
v
v
v g M
vx x vy x vz x
f x(cor)
t
x
y
z x
vy
t
z
vx
vy
x
vy
vy
y
vy
vz
z
g M
f y(cor)
y
Q
q
Q Jl
z
p p
С2
x x
x
p p
С2
y y
y
M
z
( )
( vx ) ( vy )
M
z
x
y
vx vy 1 M
vz
1 Q
z
y M
gM
x
p gM ,
gM
T
R
H
M t , x , y, z dz ,
z
( vx ) ( vy )
M
dz
x
y
z
H

16.

,
.
Aver
Ahor
Acor
2
ver
, hor
, cor
, C M
g
g
g
2
2
2
Vver Vver
Vhor Vhor
Vhor
V
2
ver
, Ahor
, Acor
, M 2
Aver
Lver
Lhor
cor
C
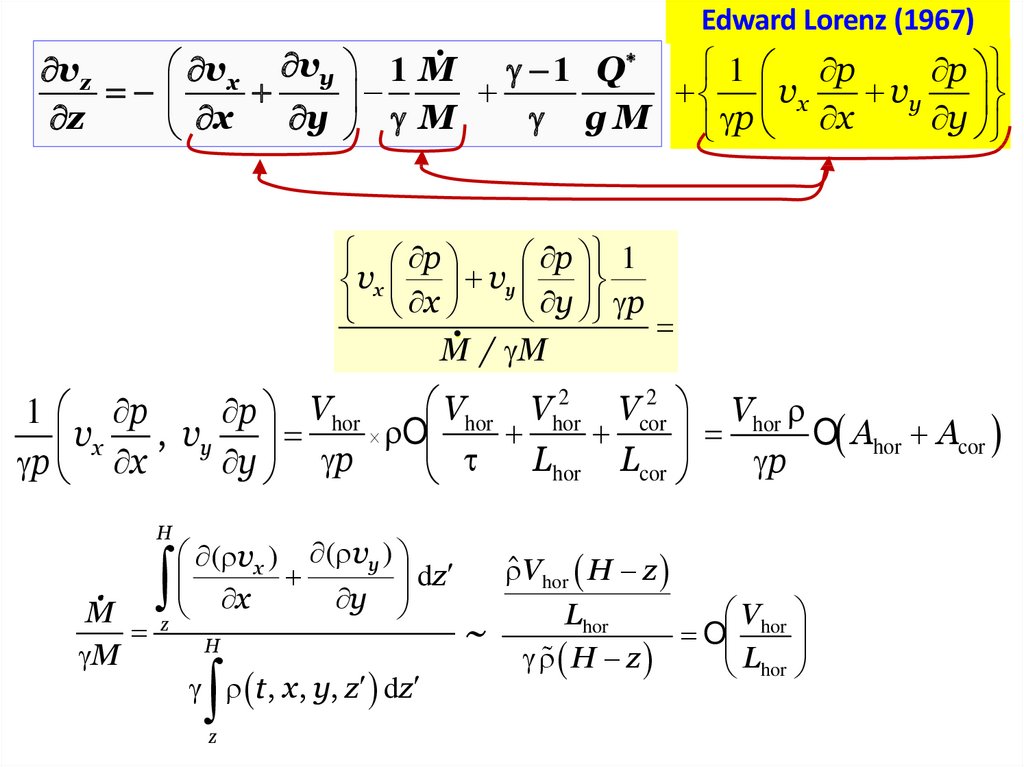
Теорема. Уравнения ( ) асимптотически точные уравнения для
ver 0,
hor 0,
cor 0,
C 0
Edward Lorenz (1967)
1 p
vx vy 1 M
v z
p
1 Q
vx
vy
p
x
y
z
x
y
M
g
M
O M2 O

17.

Edward Lorenz (1967)
1 p
vx vy 1 M
p
v z
1 Q
vx
vy
p
x
y
z
x
y
M
g
M
p
p 1
vx vy
y p
x
M / М
2
2
Vhor Vhor
Vhor
Vcor
1 p
p Vhor
O
O Ahor Acor
vx
, vy
Lhor Lcor
p
p x
y p
H
M
M
( vx ) ( vy )
dz
x
y
z
H
t , x , y, z dz
z
~
ˆVhor H z
Vhor
Lhor
O
L
H z
hor

18.

2
2
Vhor
Vhor
Vhor O
L
L
hor
cor
p
p 1
vx vy
y p
x
M / М V
O hor
Lhor
2
2
Vhor Vhor
Vhor
Vhor
O
р
Lhor Lcor
Vhor
O
L
hor
2
2
2
Lhor
Vhor
Lhor
Lhor Vhor
Vhor
Lhor
1
2 O
O 2
2 O
cor
C
Lcor
Lhor Lcor C Vhor
V
M hor ,
C
p 2
C
= 300 350 м / c
1
2
O
M

19.

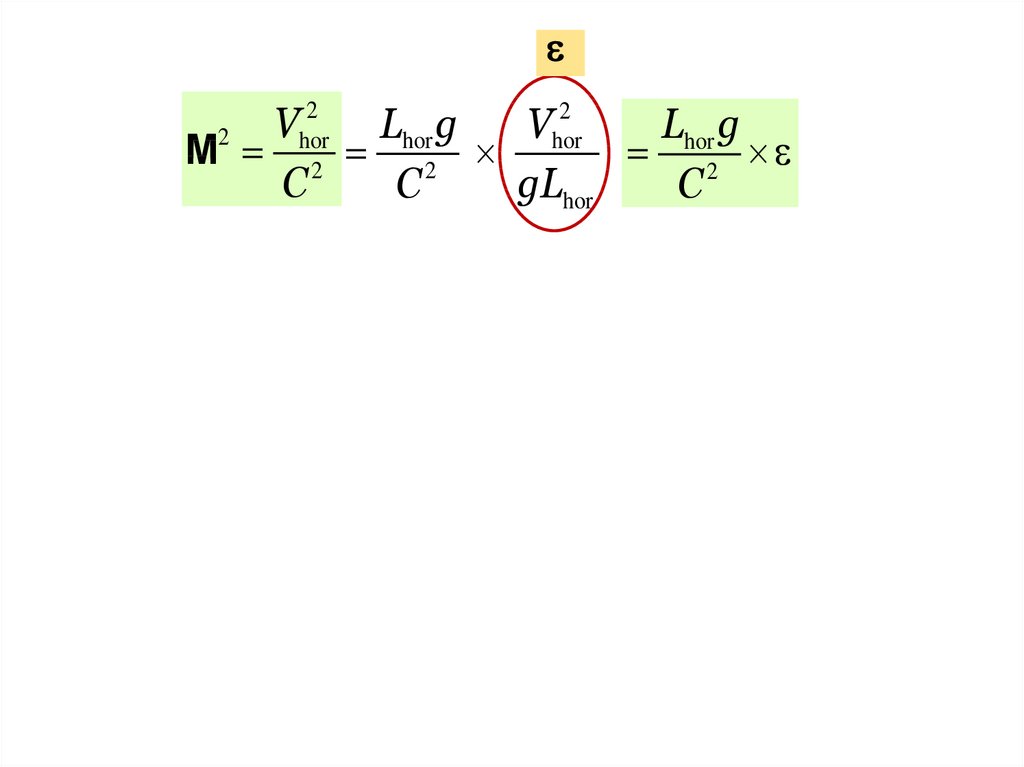
2
2
V
L
g
V
Lhor g
2
hor
hor
hor
М 2 2
2
C
C
gLhor
C

20.

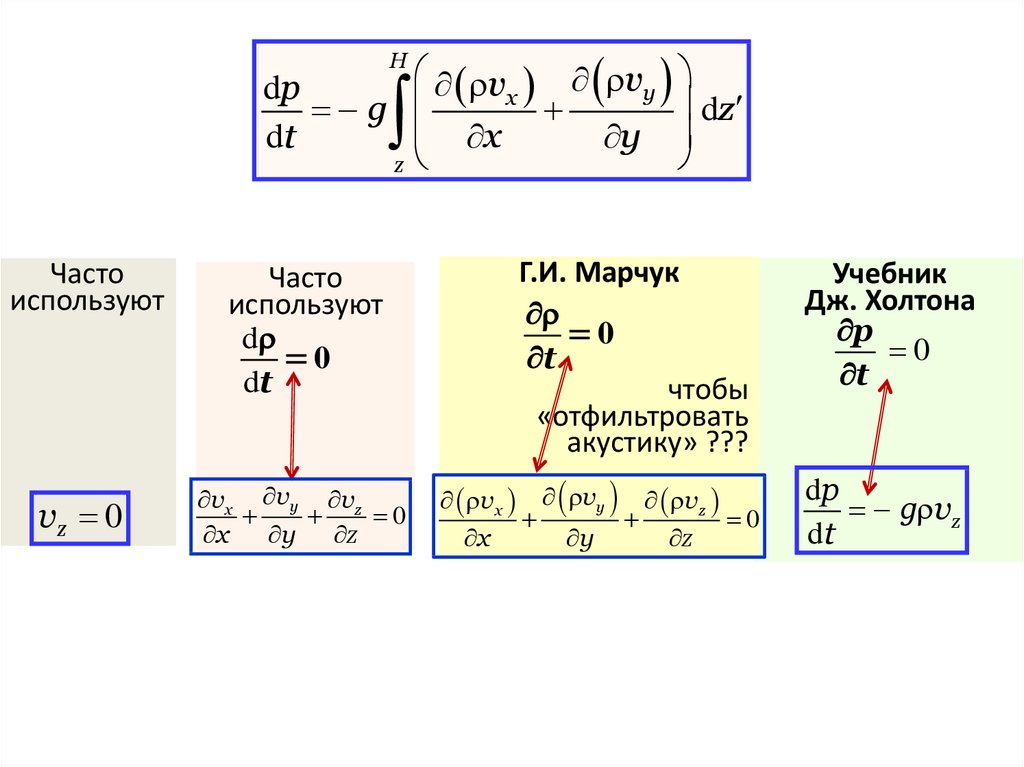
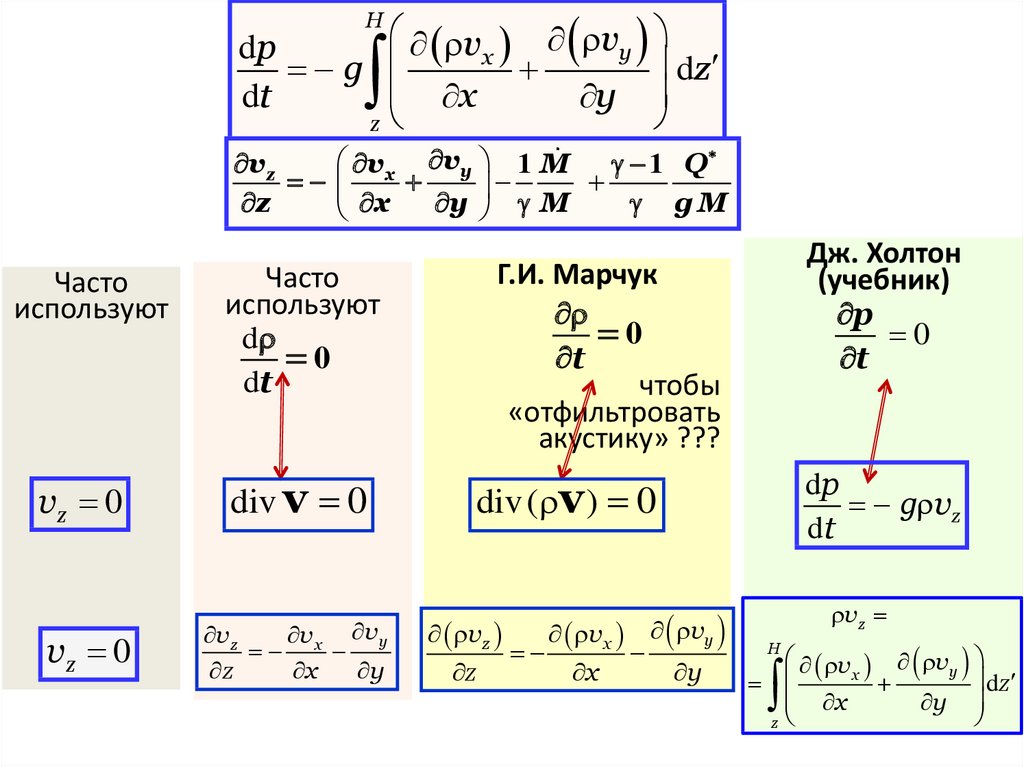
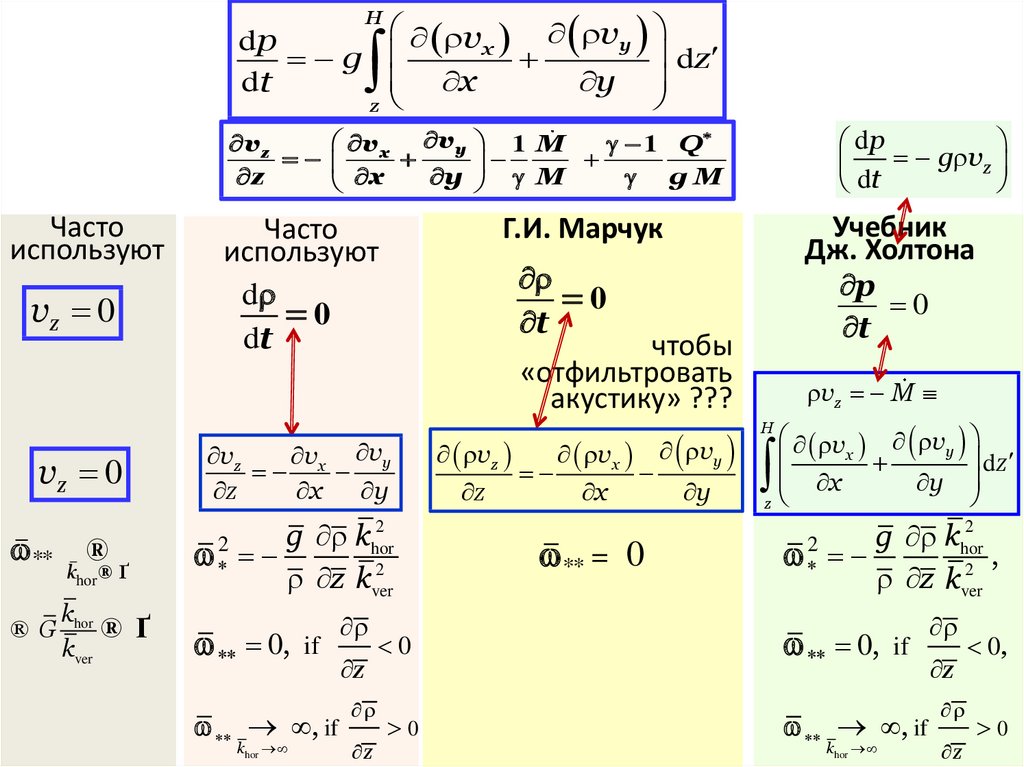
H
v vy
dp
x
g
x
dt
y
z
Часто
используют
vz 0
Часто
используют
d
0
dt
vx vy vz
0
x
y
z
dz
Г.И. Марчук
0
t
чтобы
«отфильтровать
акустику» ???
vx vy
vz
0
x
y
z
Учебник
Дж. Холтона
p
0
t
dp
g vz
dt

21.

H
v vy
dp
x
g
x
dt
y
z
dz
vx vy 1 M 1 Q
v z
z
y M
gM
x
Часто
используют
vz 0
vz 0
Часто
используют
d
0
dt
Дж. Холтон
(учебник)
p
0
t
Г.И. Марчук
0
t
чтобы
«отфильтровать
акустику» ???
dp
g vz
dt
div v 0
div ( v ) 0
v
v
vz
x y
z
x
y
vz
vx vy
z
x
y
vz
H
v vy
x
x
y
z
dz

22.

Схема распределения параметров в тропосфере
над межфазной поверхностью
МЕЖФАЗНАЯ ГРАНИЦА
- поток испаряющейся массы на
z
нижней границе атмосферы
Н
l(е) - поток энергии испарения
LvL – дождевой (снежный) поток
q - поток тепла
G - коротковолновая солнечная радиация
U - длинноволновое тепловое излучение
р 0,
0
p
Lver
НЕПРОЗРАЧНАЯ
(твердая) фаза:
G = U = 0
T
G+0
AG+0
G 0
U+0
U 0
LvL
q+0 (е)
l
+
q 0
q 0 q 0 (1 A)G 0 G 0 U 0 U 0 0(e)l (e) 0(m)l (m)

23.

U
U
U
U
Bt
Bx
By
Bz
B = 0,
t
x
y
z
ж чц
зз ч
зз vх чч
зз ччч
зз vy чч
U = зз ччч,
зз vz ч
зз ччч
зз M&чч
зз чч
зиM чш
ж
ц
&
зз Q - M / ( M )ч
ч
ч
зз
ч
ч
зз
ч
- vy f
ч
зз
ч
ч
ч
зз
vx f
ч
ч
B = зз
ч
зз- Q - M
& / M ч
ч
ч
(
)
зз
ч
ч
ч
зз
ч
ч
0
зз
ч
ч
зз
ч
ч
и
ш
(
)
(
)

24.

1
0
0
Bt
0
0
0
vz
0
0
Bz
0
0
0
0 0 0 0 0
1 0 0 0 0
0 1 0 0 0
,
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0
0
vz
0
0
vz
0
0
0
0
0
0
0 0 0
0 0 0
0 0 0
1 0 0
0 1 0
0 0 1
vx
0
0
Bx
0
vx
0
vy
0
0
Bx
0
vy
0
0
0
0 0
vx
0
0 0
0
vx
0 0
1
0
0
0 0
0 0
0
0
0 0
0
0
0 0
vy
0
0 0
0
vy
0 0
0
0
1 0 0
0 0
0
0
0 0
0
g /
0
0
0
0
0
0
g /
0
0
0

25.

B =
B11
B21
B31
0
vx vy
x
y
1
&
Q
M
B11
,
M M
x
vx
x
vy
f
x
y
vx
f
y
vy
z
vx
z
vy
y
z
0
0
0
1
M
0
0
0
0
x
0
y
0
1 dvx
B21
vy f
dt
,
M
0
0
B11
M
0
0
B11
M
0
0
1 dvy
B31
vx f
dt
,

26.

1. В дифференциальном операторе системы уравнений
квазистатического по вертикали движения нет
скорости
звука
С,
даже
в
уравнениях
горизонтального движения,
т.е. уже «акустика отфильтрована» (выражение Г.И. Марчука).
2. Система уравнений только с вертикальной
квазистатичностью негиперболична (С )
даже при отсутствии теплопроводности, т.е. при
отсутствии параболического члена
T
∂xk xk

27.

Некоторое решение
U = U (t , x , y , z )
Другое решение, отличающееся от U малым возмущением
U (d) = U + Uў,
(U :
1, Uў = 1).
U
U
U
U
Bt
Bx
By
Bz
B U F
t
x
y
z
ж ў ц
зз ч
ч
зз vў ч
ч
х ч
зз ч
зз vyў ч
ч
ч
з
U= з ч
,
ч
ч
зз vzў ч
зз ч
ч
&
зз M ўч
ч
ч
зз ч
ч
ч
зиM ўш
ж- Q ў/ M ч
ц
зз
ч
ч
зз
ч
0
ч
зз
ч
ч
зз
ч
0
ч
ч
F ў= зз
ч
зз Q ў/ M ч
ч
ч
зз
ч
ч
0
зз
ч
ч
ч
зз
ч
и
ш

28.

Исходное гармоническое возмущение
жA ( ) ц
ч
зз
ч
зз A (vx ) ч
ч
ч
зз
ч
(
vy
)
зз A ч
ч
ч
A = зз (vz ) ч
,
ч
ч
зз A ч
зз (M&) ч
ч
зз A ч
ч
ч
зз (M ) ч
ч
ч
иA ш
Коротковолновые возмущения с Q = 0:

29.

Коротковолновые возмущения
6444444444444447 444444444444448
Bt , B x , B y , B z , Bў, » const, F ў= 0
vxў = A*(vx ) E* , vyў = A*(vy ) E* , vzў = A*(vz ) E*
&
ў= A*( ) E* , M&ў= A*(M ) E* , M ў= A*(M ) E*
E* = exp i (kx x + ky y + kz z - *t ) = exp ( **t )Чexp i (kx x + ky y + kz z - t ) ,
(
)
* = + i ** ,
(
* = * Ч
** > 0 - неустойчивость (коротковолновая) решения U (t , x , y , z )
** ® + Ґ - абсолютная неустойчивость решения U (t , x , y , z )
k® Ґ
некорректно поставленная задача
)

30.

DA * = 0,
(
( )
*
(vx )
*
A* = A , A
(vy )
*
,A
(vz )
*
,A
&)
(M
*
,A
(M )
*
,A
T
).
D i Bt kx Bx kyBy kz Bz B
det D = 0
b, c , d определяется значениями компонент U ,
vx vy
а именно , vx , vy , vz ,
,
,...
x x

31.

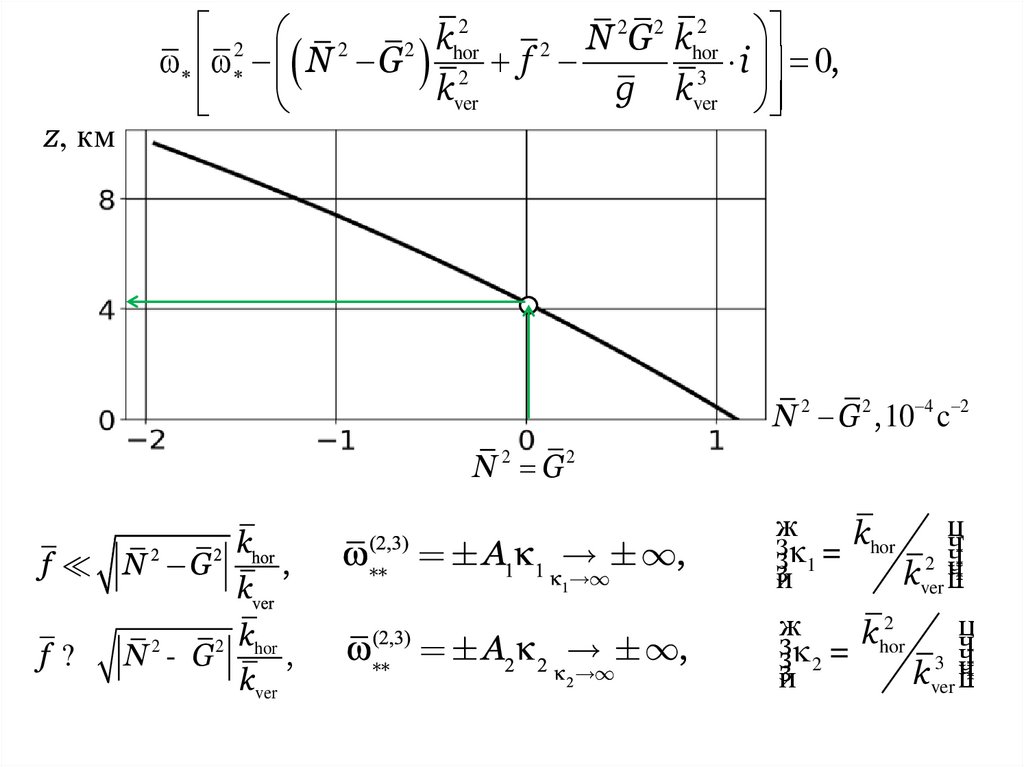
Устойчивость покоя
& 0, Q 0
vx vy vz 0,
0, M
x y
vx vy
vx vx vx vy vy vy vz
0,
0,
t
t
x
y
z
x
y
z
z
+ стандартная атмосфера (z ),
и
z
p
2
2
2 2
2 2
k
k
N
G
2
2
hor
hor
N G
f
i 0,
2
3
g kver
kver
2
g Lver 2
N
N
z Lhor
2
2
g Lver
2
G
g
M Lhor p
2
g
N
,
z
2 g 2 g2
G
,
p
C

32.

2
2
2 2
2 2
k
k
N
G
2
2
hor
hor
N G
f
i 0,
2
3
g kver
kver
z, км
N 2 G 2 , 10 4 c 2
N 2 G2
f?
N 2 - G2
khor
,
kver
ж
ц
зз 1 = khor 2 чч
зи
kver чш
2
ж
ц
k
зз 2 = hor 3 ч
ч
ч
зи
kver ш

33.

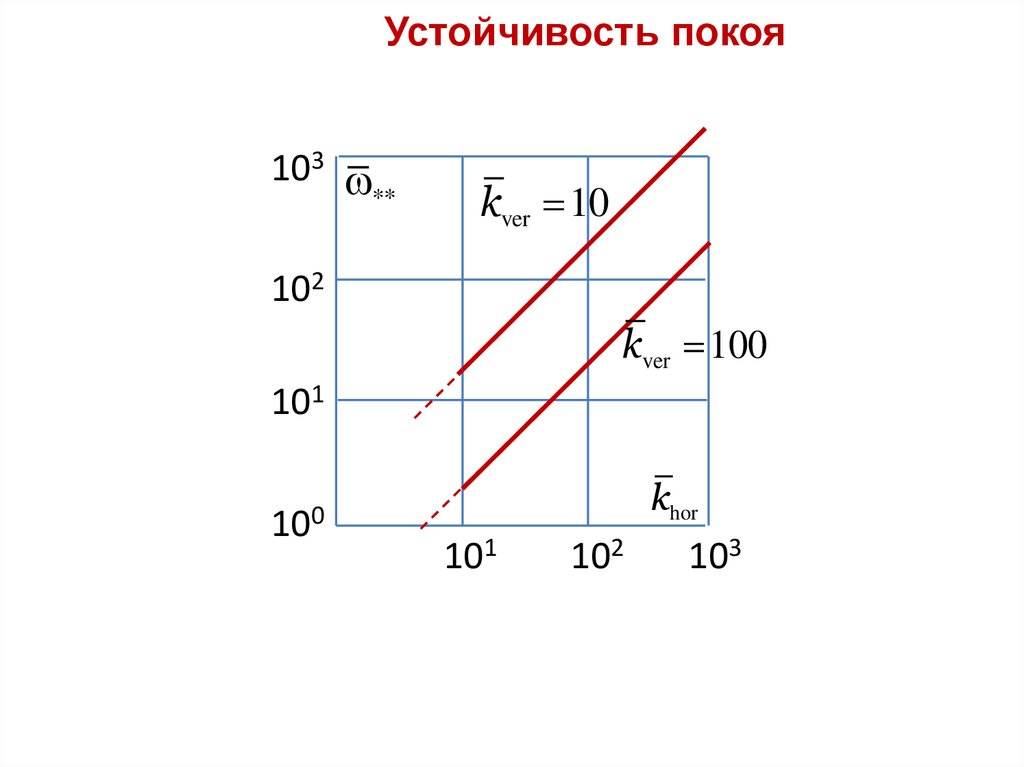
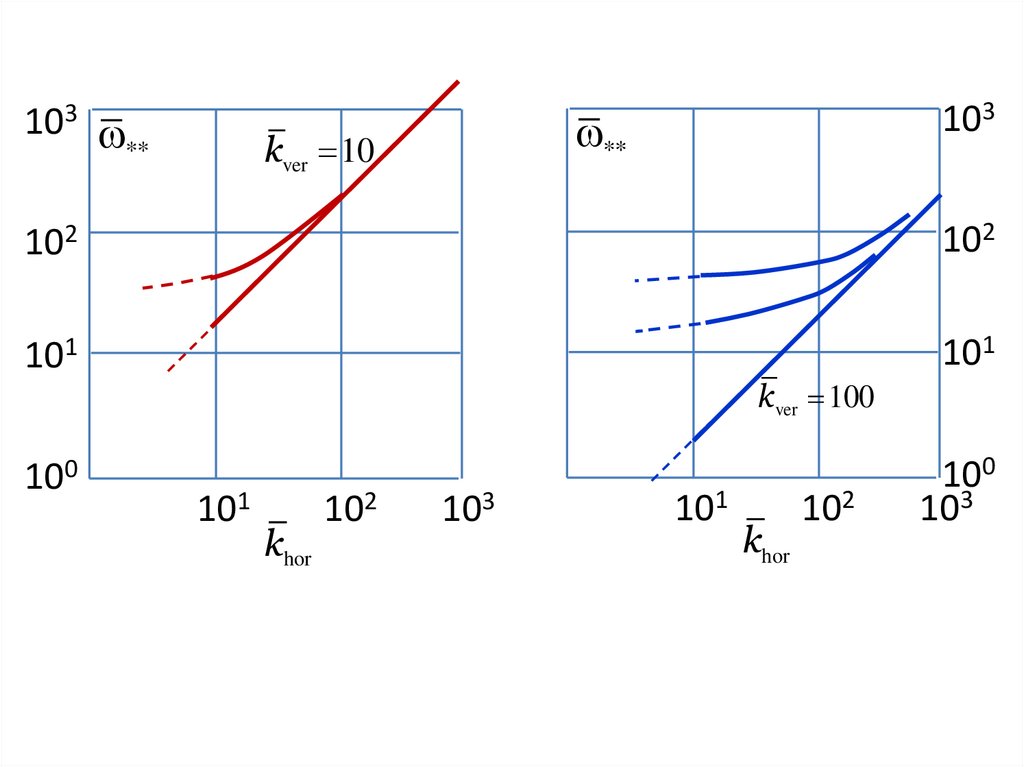
Устойчивость покоя
103
**
kver 10
102
kver 100
101
100
khor
101
102
103

34.

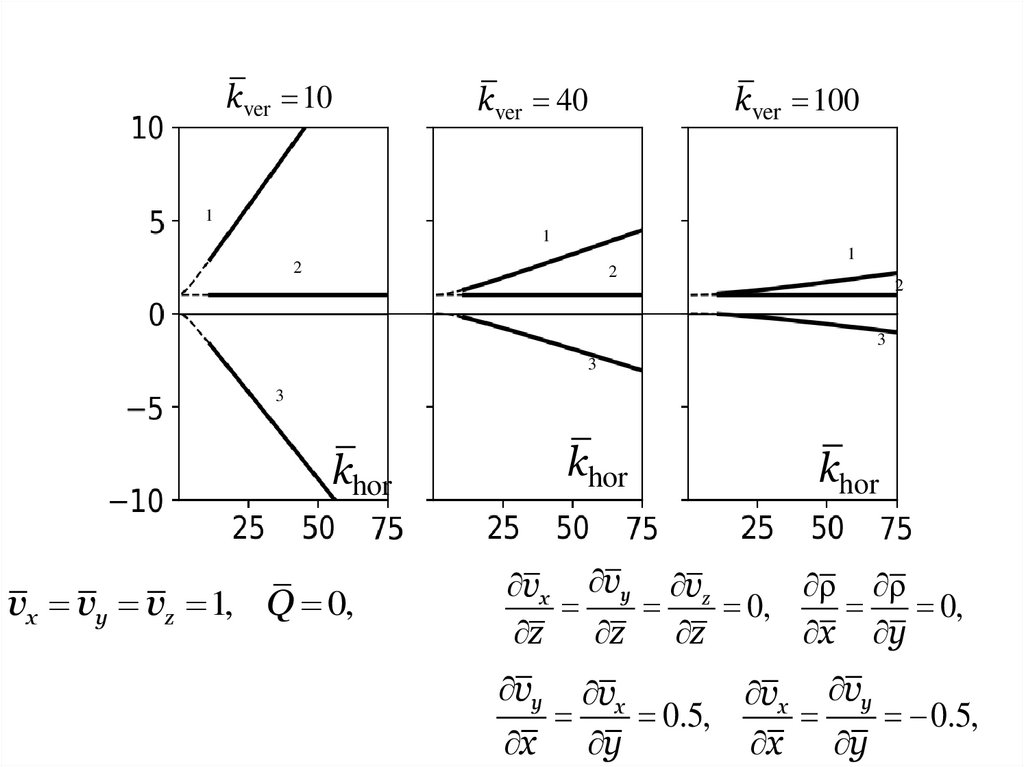
kver 10
kver 40
kver 100
1
1
1
2
2
2
3
3
3
khor
khor
vx vy vz 1, Q 0,
khor
vx vy vz
0,
0,
z
z
z
x y
vy
vx
vx vy
0.5,
0.5,
x y
x y

35.

103
**
103
**
kver 10
102
102
101
101
100
kver 100
101
khor
102
103
101
khor
102
100
103

36.

РАЗНОСТНАЯ СЕТКА
vi
xi
i
li min 4 i ,
kimax li min 2 ,
i x , y , z ,
kimax kimax Li 1 2 N i
Li
Ni ,
i
ki kimax 1 2 N i
i x , y, z ,

37.

ИСКУССТВЕННАЯ ВЯЗКОСТЬ
c a kx kykz
a
a
Vver Lver
n
,
c a k x ky k z
m
( a 1.8 10 5 кг / (м с) ).
,

38.

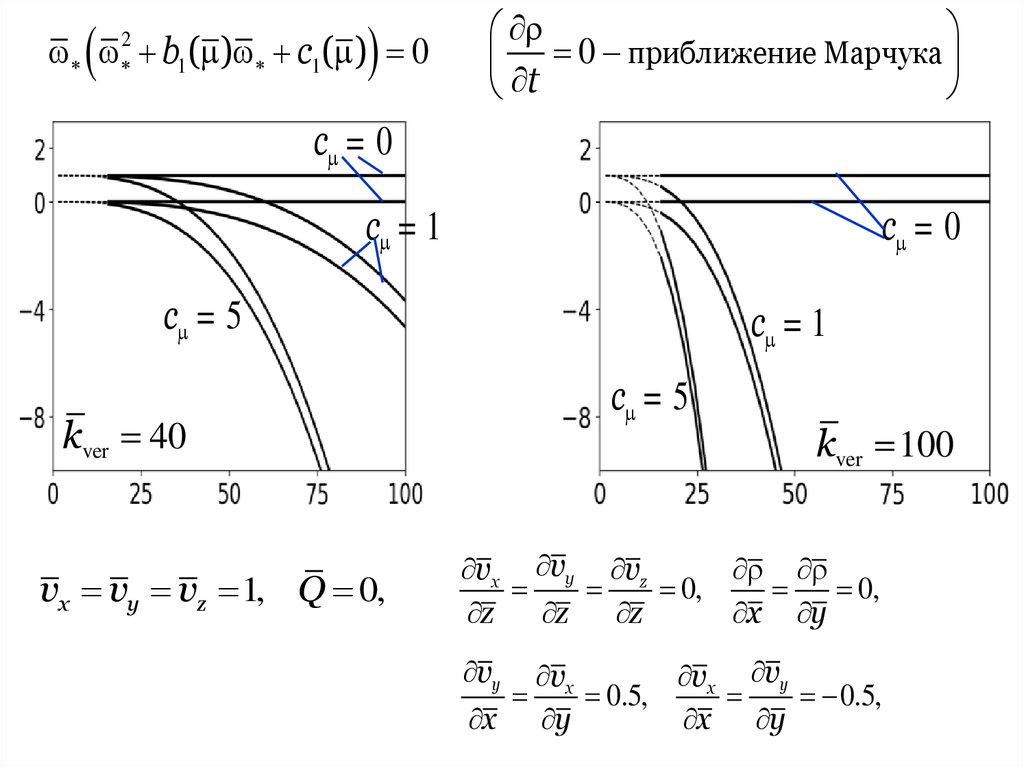
kver 10
n 1.5
c = 1
c = 0
c = 5
1
1
1
2
2
2
3
3
3
khor
khor
khor

39.

b1( ) c1( ) 0
2
0 приближение Марчука
t
c = 0
c = 0
c = 1
c = 5
c = 1
c = 5
kver 40
vx vy vz 1, Q 0,
kver 100
vx vy vz
0,
0,
z
z
z
x y
vy
vx
vx vy
0.5,
0.5,
x y
x y

40.

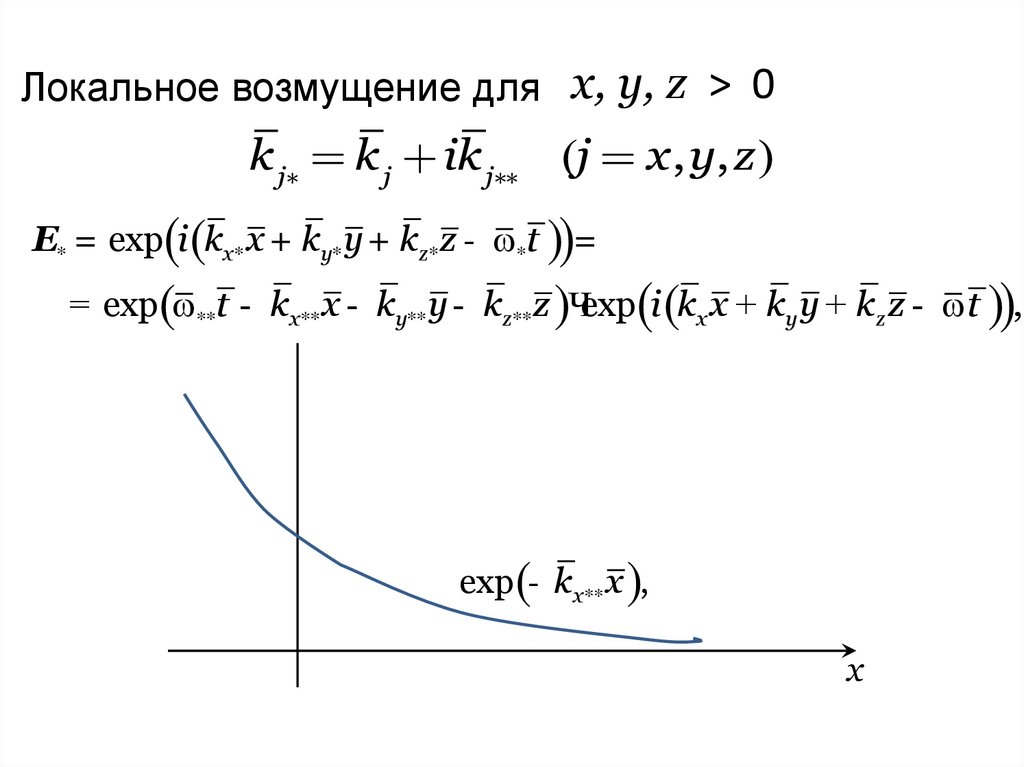
Локальное возмущение для x, y, z > 0
E* = exp i (kx* x + ky* y + kz* z - *t ) =
(
)
= exp( **t - kx** x - ky**y - kz** z )Чexp i (kx x + ky y + kz z - t ) ,
(
)
exp (- kx** x ),
x

41.

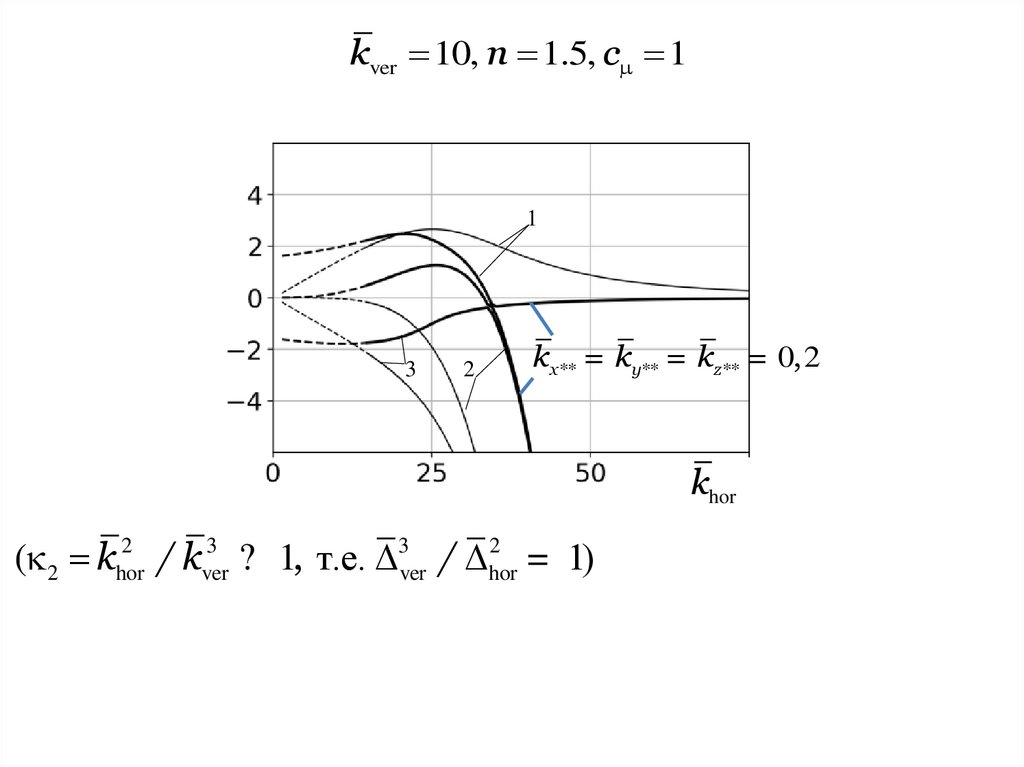
kver 10, n 1.5, c 1
1
3
2
kx** = ky** = kz** = 0, 2
khor
2
3
2
( 2 khor
/ kver
? 1, т.е. 3ver / hor
= 1)

42.

H
v vy
dp
x
g
x
dt
y
z
vx vy
v z
z
x
y
Часто
используют
vz 0
vz 0
** ®
khor ® Ґ
®G
khor
® Ґ
kver
, if
khor
z
z
Учебник
Дж. Холтона
p
0
t
чтобы
«отфильтровать
акустику» ???
2
g khor
2
z kver
if
dp
g
v
z
dt
1M
1 Q
M
gM
0
t
vx vy
vz
z
x
y
0,
Г.И. Марчук
Часто
используют
d
0
dt
2
dz
0
0
vz
vx vy
z
x
y
** = 0
vz M
H
v vy
x
x
y
z
2
dz
2
g khor
,
2
z kver
0,
if
, if
khor
z
z
0,
0

43.

Негиперболичность приводит к некорректной (ill posed) поста-
новке задачи Коши при отсутствии диссипации, при которой коротковолновые
возмущения
Wk t 0 A k sin kx
при k
растут неограниченно быстро:
W A k exp (k )t sin kx ,
(k )
k
p
L 0 ~ H ~ 104 м - линейный размер, следующий из дифференциального
0 g
оператора и начальных условий
2 2 0 g
k
- характерное волновое число метеорологического процесса
L
p0
Конечно-разностная схема генерирует «паразитные»
коротковолновые возмущения с длинами волн l > 4 x и волновым
2
2
числом
kx
и
kz
lx
lz
2 0 g
2
2
если k
или
k
, то 1, exp (k ) 1
4
z
4
x
p
0
Необходим фильтр (численная диссипация) для возмущений типа
A k sin kx при k x 1
A k 0
при k

44.

Луна и Земля
Снимок с борта Discovery 16.07.15 из точки Лагранжа (1,5 млн км от Земли).
H = 300 км
Толщина
стратосферы
1/ H
30
СПАСИБО
ЗА ВНИМАНИЕ !