Химическая связь и строение молекул

1. Химическая связь и строение молекул

Лекция 7

2. Химическая связь

3. Потенциальная кривая

U ( r ) D e 1 e
( r re ) 2

4.

5. Атомная орбиталь

АО = nlm

6. Спин – орбиталь электрона.

(i)
( ) ms = +1/2 а.е.
( ) ms = -1/2 а.е.
Пример
( )
В общем случае 1 (1)

7. Полная волновая функция атома и молекулы.

Состояние системы содержащей
несколько электронов описывается
полной волновой функцией,
учитывающей квантовые состояния
для всех электронов, т.е. совокупностью спин-орбиталей I .
ат = П I ; мол = П I

8. Метод валентных схем (МВС)

Рассмотрим молекулу Н2, которую
построим из двух АО атомов Н.
AO для Н1 – 1s0 и 1 = 1s0,a* (1)= 1s0,a(1)= H,a (1)
для Н2 – 1s0 и 2 = 1s0,b * (2)= 1s0,b(2) = H,b (2)
H2
*
1
2

9. Метод молекулярных орбиталей (ММО)

1
Ha
(1) (1)
Hb
H2
*
2
1
Ha
2
(2) (2)
Hb

10. Метод молекулярных орбиталей

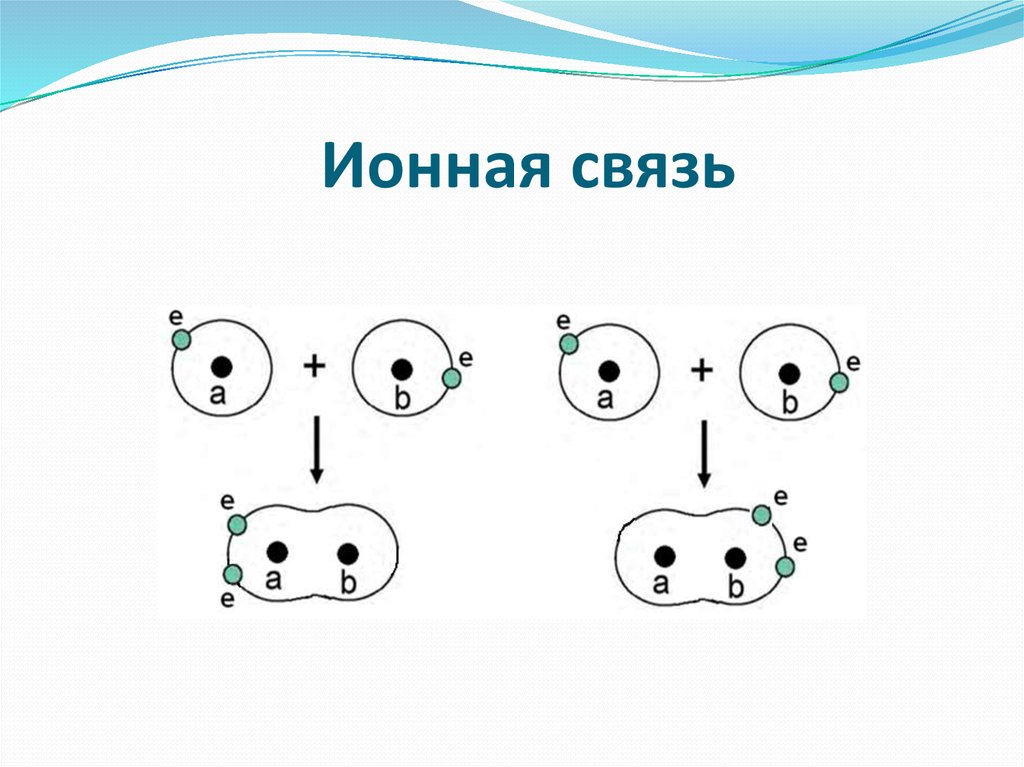
11. Ионная связь

12. МВС

Связь образуется между атомами, имеющими
неспаренные электроны с антипараллельными
спинами.
Образование химической связи обусловлено
повышенной электронной плотностью между
ядрами. Возникает ковалентная двухэлектронная двухцентровая связь, которую наглядно
можно изобразить в виде черточки
валентности Н-Н.
Прочность химической связи в большой
степени определяется перекрыванием
электронных облаков взаимодействующих
атомов, или АО.

13.

Метод валентных схем (МВС)

14. Гипервалентность и гибридизация ОА

15. Донорно-акцепторное взаимодействие

16.

17. Метод молекулярных орбиталей

H = Te1 +Te2 + Uaei + Ue1e2 + Uab
H = -1/2∇2е1-1/2∇2е2 - Za/ri + 1/r12 + Z2/R в а.е.

18. Точное решение уравнения Шредингера

Точное решение уравнения
Шредингера для многоэлектронной
молекулы решить невозможно
Причина:
Потенциальная энергия взаимодействия между электронами е1 и е2
Ueiej = 1/rij

19. Решение для Н2+

Решение для
+
Н2
Ĥ М(r, , ) = E М(r, , )
H = -1/2∇2е1- (Za/r1 + Zb/r2 ) +Z2/R (в а.е.)
Общий подход к решению молекулярных
структур
М = R(r) ( ) ( ) = Z( )H( ) ( ) = f(n,l, )
Сферические Цилиндрические
координаты
коoрдинаты

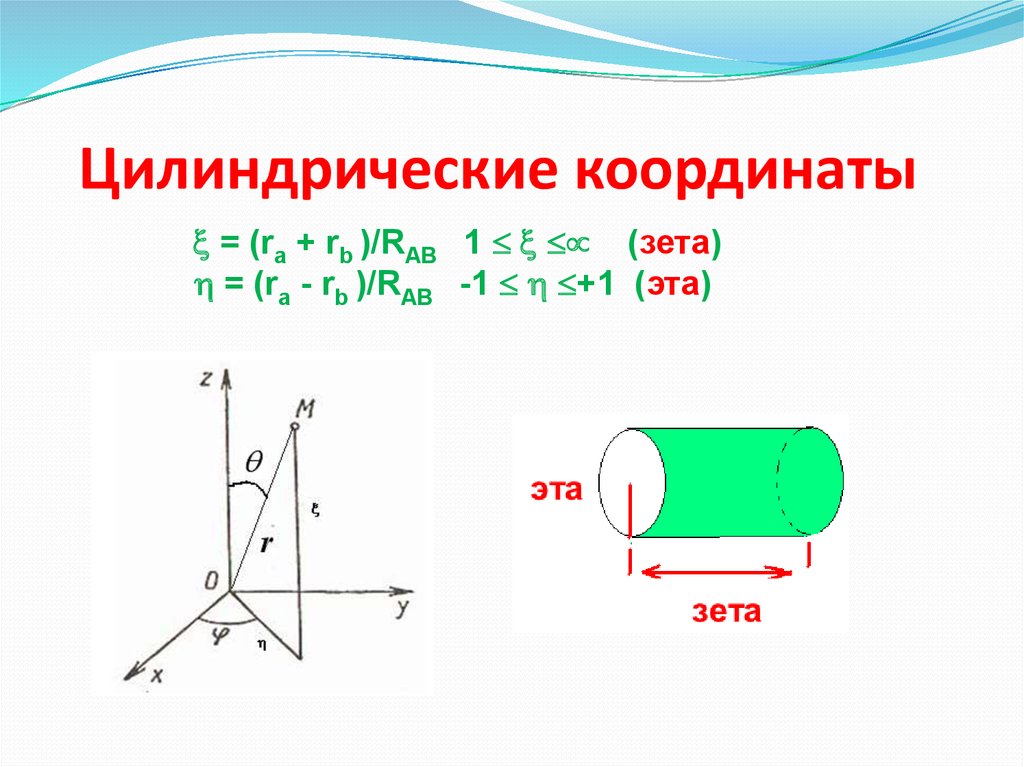
20. Цилиндрические координаты

= (ra + rb )/RAB 1 (зета)
= (ra - rb )/RAB -1 +1 (эта)

21. Анализ решения

Для молекулы квантовые числа n и l
не имеют физического смысла и не
постоянные.
Квантовое число является
решением ( ) = Аexp(i ) и
называется осевым квантовым
числом | | = 0, 1, 2, 3

22. Обозначение МО для двухатом-ных молекул

Обозначение МО для двухатомных молекул
| |
МО
0 1
2
3
МО = N
где N – номер МО по мере возрастания энергии.
- индекс указывающий симметрию относительно
операции инверсии î. Возможны два случая:
î = +1* ( g – четная) или
î = -1* (u – нечетная) функция

23. Осевое квантовое число 

Осевое квантовое число
Квантовое число в молекуле может быть
сопоставлено с кв.числом m в атоме, если
расположить молекулу по оси Z и
рассмотреть проекцию на плоскость XY
î = +1*

24. Осевое квантовое число =1

Осевое квантовое число = 1
2 u,x = 2px1 + 2px2 =+1 ; 2 u,y = 2py1 + 2py2 =-1
î = -1*