Similar presentations:
Построение теней от геометрических тел. Построение теней на архитектурных деталях. Лекция 13
1. Лекция 13
•Построение теней от геометрических тел•Построение теней на архитектурных
деталях
•Построение теней на лестнице. Метод
вспомогательных экранов
•Построение теней на колоннах,
пилястрах
2. Способ вспомогательного проецирования
В этом способе используютсядополнительные проекции светового
луча на плоскости П2 и П3.
Т.к. за направление светового луча
принята диагональ куба, всегда можно
построить недостающие проекции
луча, имея одну вторичную проекцию и
луч S
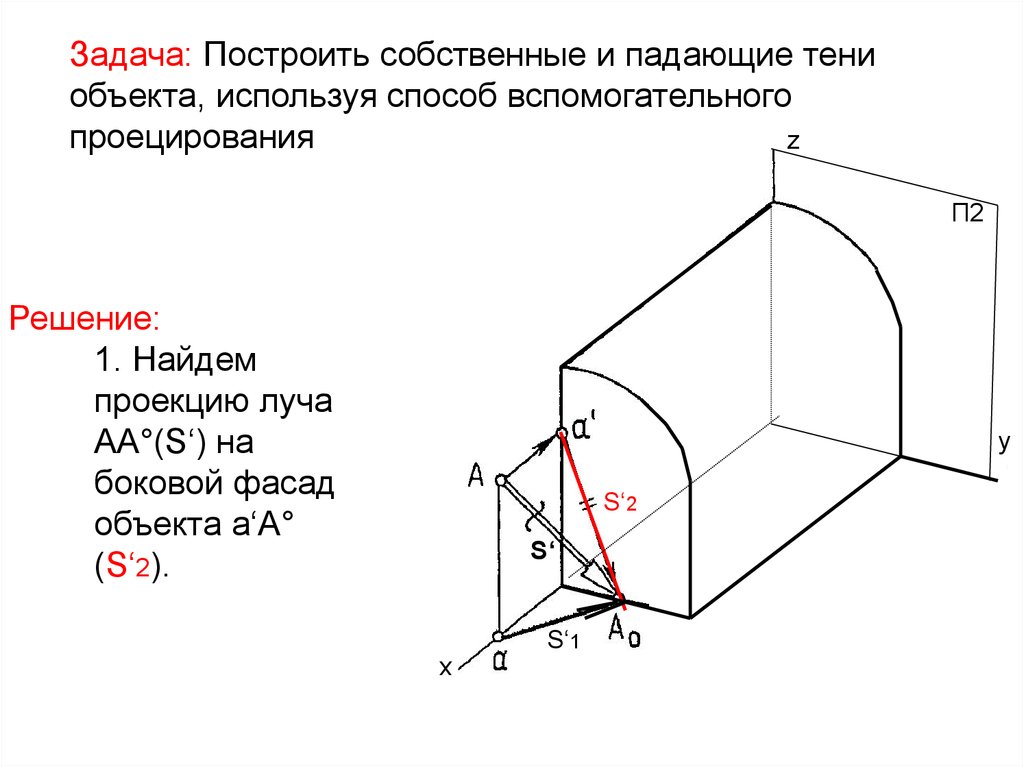
3. Решение: 1. Найдем проекцию луча АА°(S‘) на боковой фасад объекта а‘А° (S‘2).
Задача: Построить собственные и падающие тениобъекта, используя способ вспомогательного
проецирования
z
П2
Е≡Е°2
Решение:
1. Найдем
проекцию луча
АА°(S‘) на
боковой фасад
объекта а‘А°
(S‘2).
S‘2
S‘
S‘1
x
М°y2
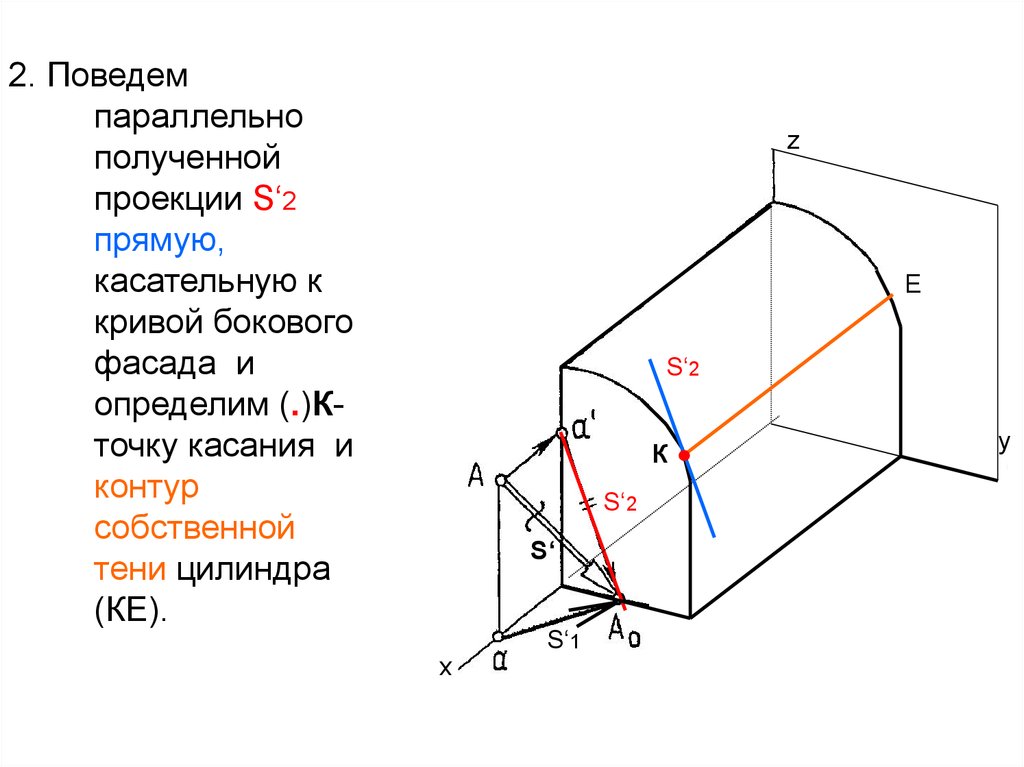
4. 2. Поведем параллельно полученной проекции S‘2 прямую, касательную к кривой бокового фасада и определим (.)К- точку касания и
2. Поведемпараллельно
полученной
проекции S‘2
прямую,
касательную к
кривой бокового
фасада и
определим (.)Кточку касания и
контур
собственной
тени цилиндра
(КЕ).
z
Е≡Е°
2
Е
S‘2
К ●
S‘2
S‘
S‘1
x
М°y2
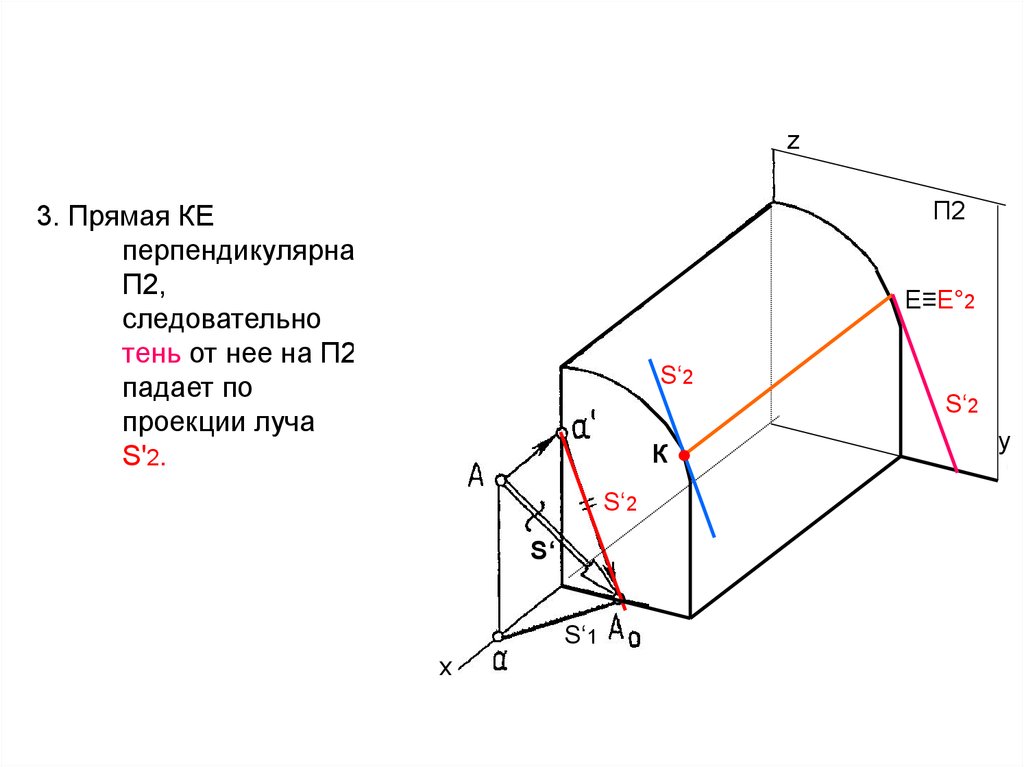
5. 3. Прямая КЕ перпендикулярна П2, следовательно тень от нее на П2 падает по проекции луча S'2.
zП2
3. Прямая КЕ
перпендикулярна
П2,
следовательно
тень от нее на П2
падает по
проекции луча
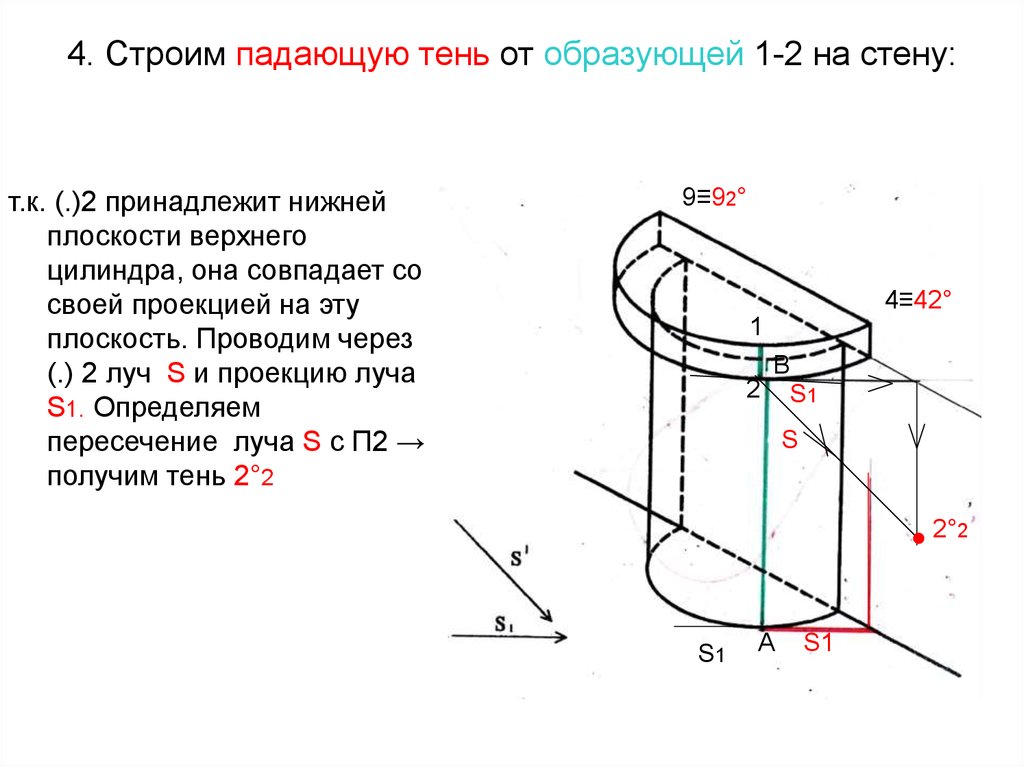
S'2.
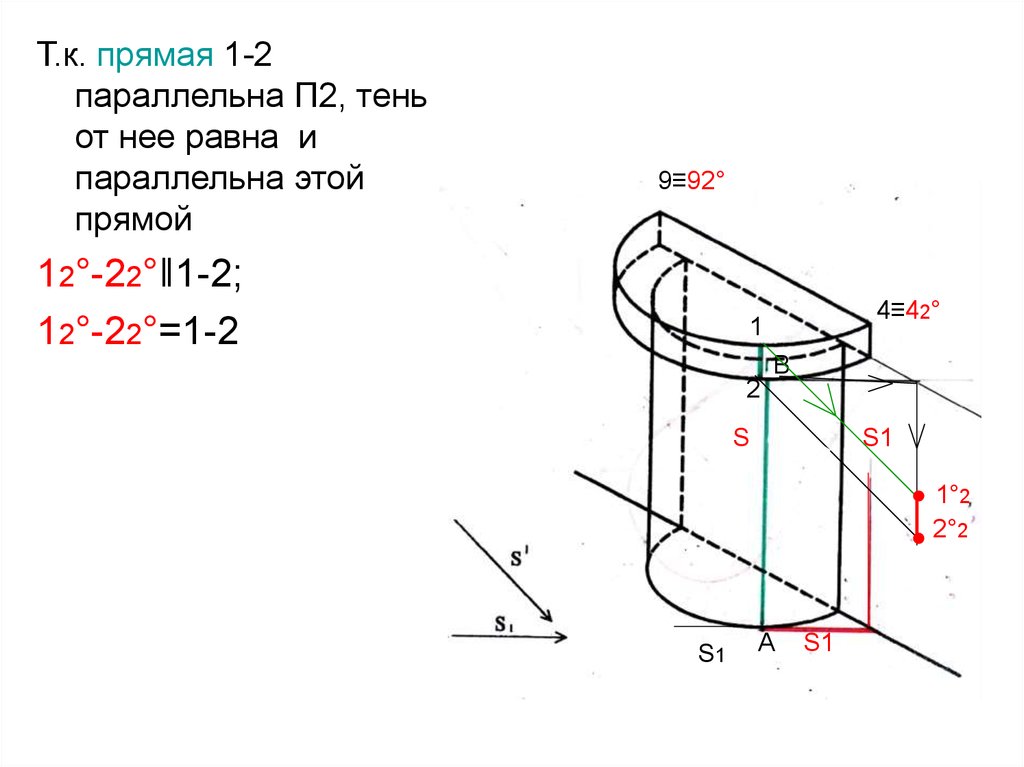
Е≡Е°2
Е≡Е°2
S‘2
К ●
S‘2
S‘
S‘1
x
S‘2
М°y2
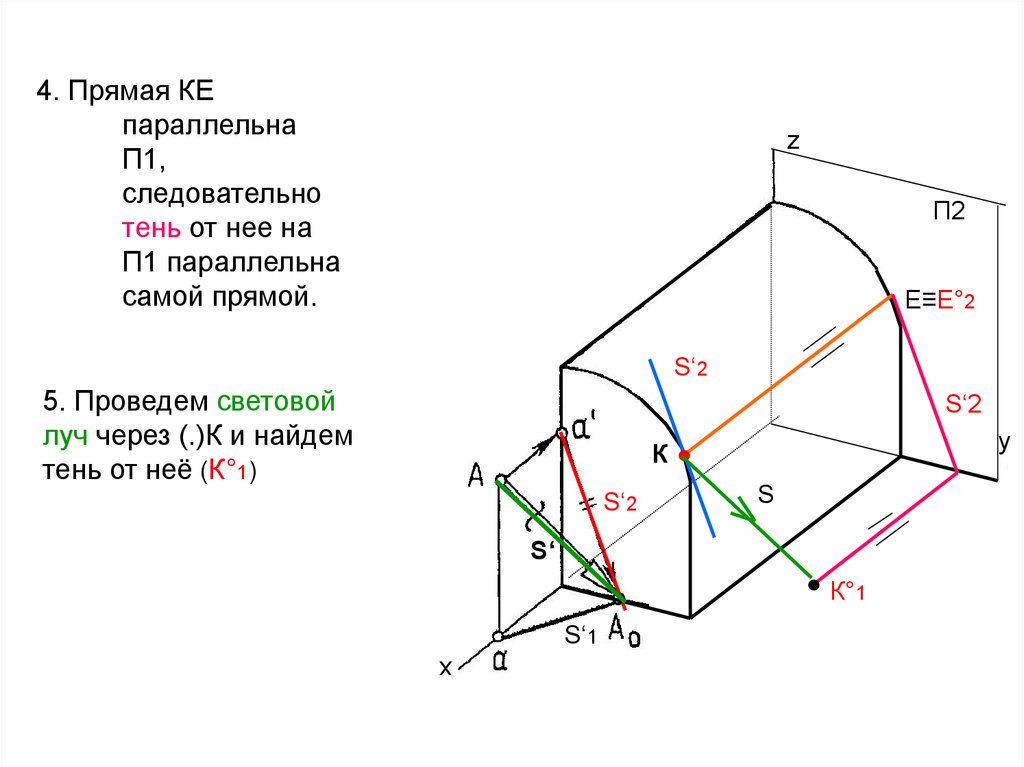
6. 4. Прямая КЕ параллельна П1, следовательно тень от нее на П1 параллельна самой прямой.
zП2
Е≡Е°2
Е≡Е°2
S‘2
5. Проведем световой
луч через (.)К и найдем
тень от неё (К°1)
S‘2
М°y2
К ●
S‘2
S
S‘
● К°1
S‘1
x
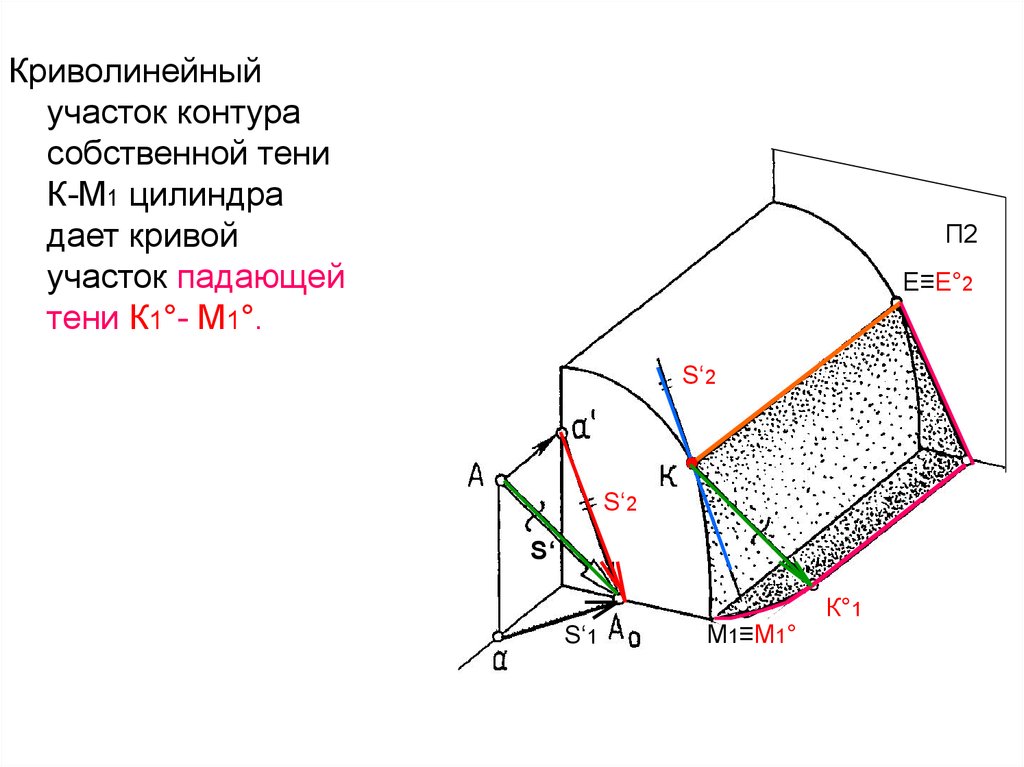
7.
Криволинейныйучасток контура
собственной тени
К-М1 цилиндра
дает кривой
участок падающей
тени К1°- М1°.
П2
Е≡Е°2
S‘2
S‘2
S‘
S‘1
M1≡M1°
К°
11°
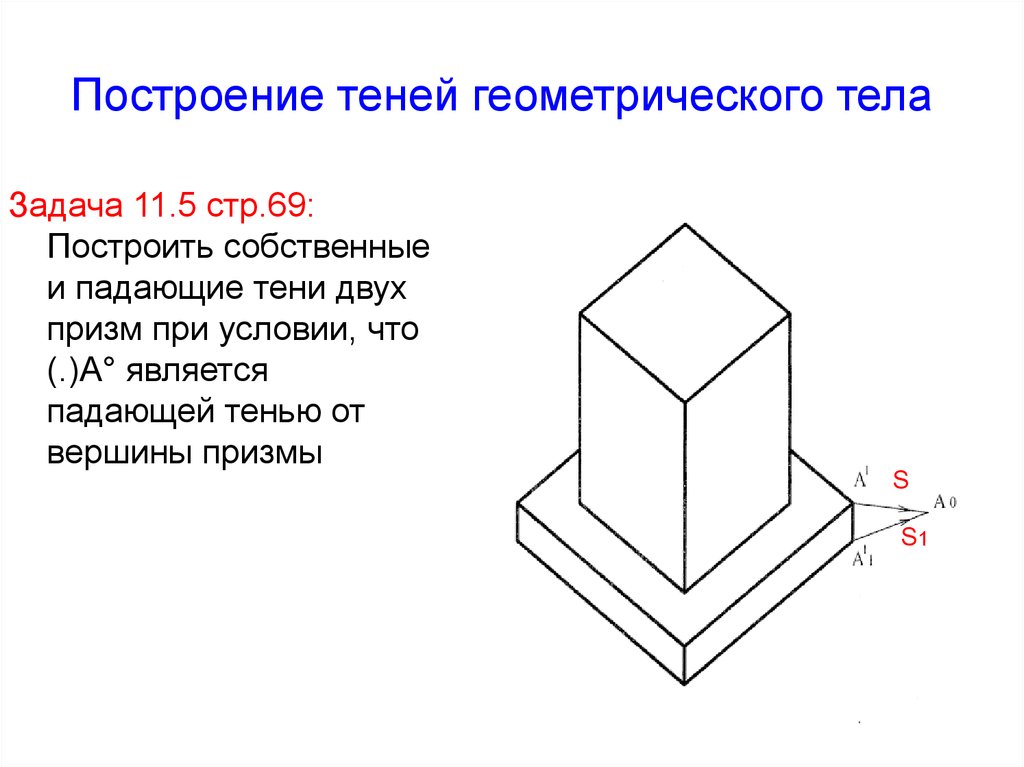
8. Построение теней геометрического тела
Задача 11.5 стр.69:Построить собственные
и падающие тени двух
призм при условии, что
(.)А° является
падающей тенью от
вершины призмы
S
S1
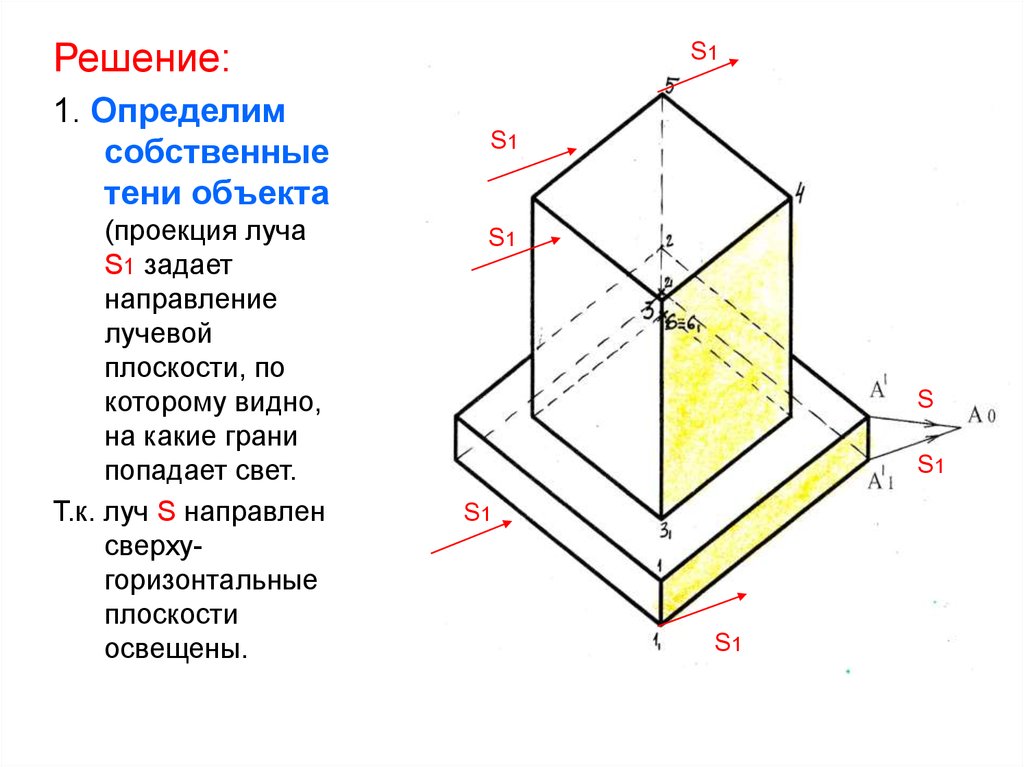
9.
Решение:1. Определим
собственные
тени объекта
(проекция луча
S1 задает
направление
лучевой
плоскости, по
которому видно,
на какие грани
попадает свет.
Т.к. луч S направлен
сверхугоризонтальные
плоскости
освещены.
S1
S1
S1
S
S1
S1
S1
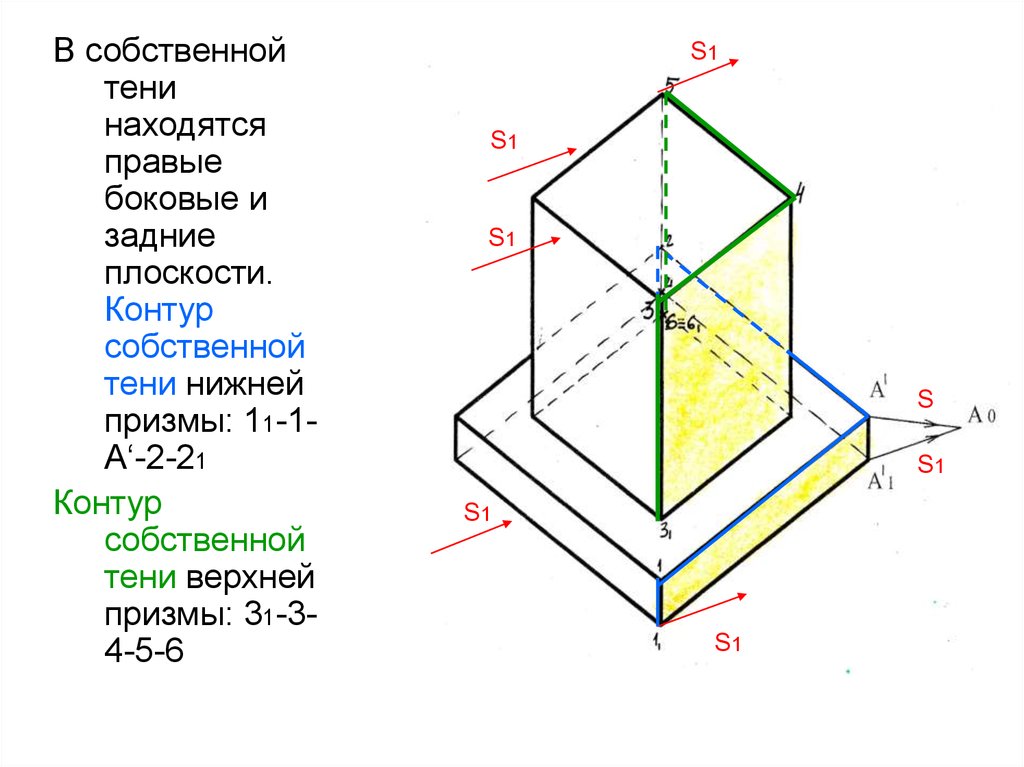
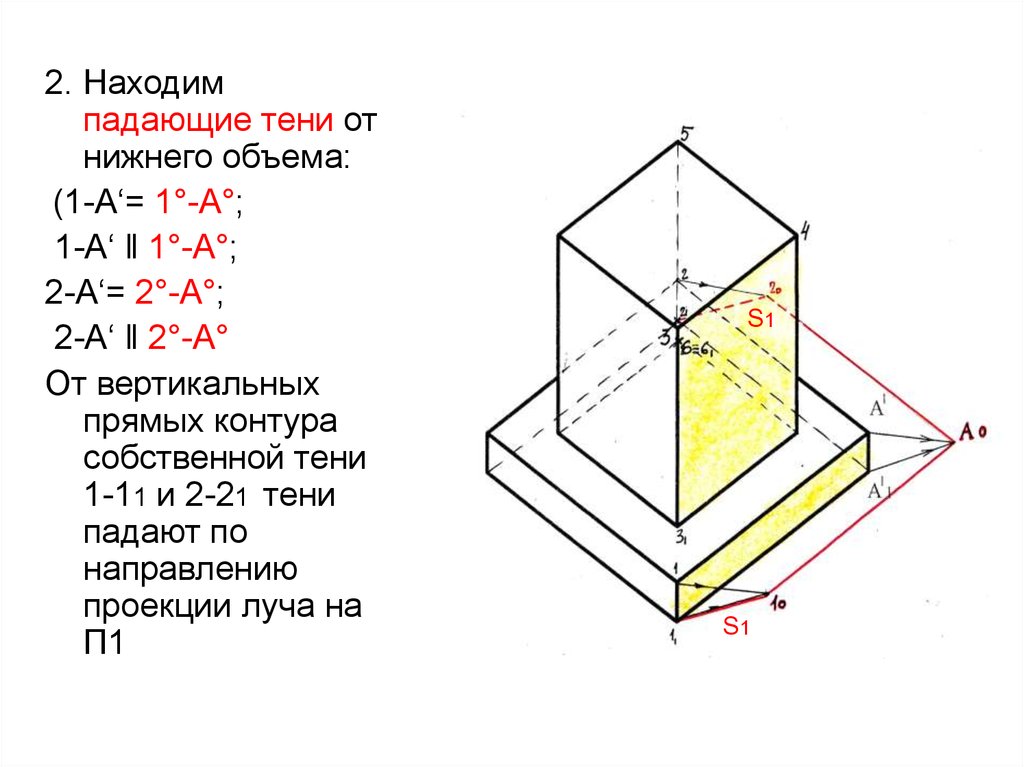
10.
В собственнойтени
находятся
правые
боковые и
задние
плоскости.
Контур
собственной
тени нижней
призмы: 11-1А‘-2-21
Контур
собственной
тени верхней
призмы: 31-34-5-6
S1
S1
S1
S
S1
S1
S1
11.
2. Находимпадающие тени от
нижнего объема:
(1-А‘= 1°-А°;
1-А‘ ‖ 1°-А°;
2-А‘= 2°-А°;
2-А‘ ‖ 2°-А°
От вертикальных
прямых контура
собственной тени
1-11 и 2-21 тени
падают по
направлению
проекции луча на
П1
S1
S1
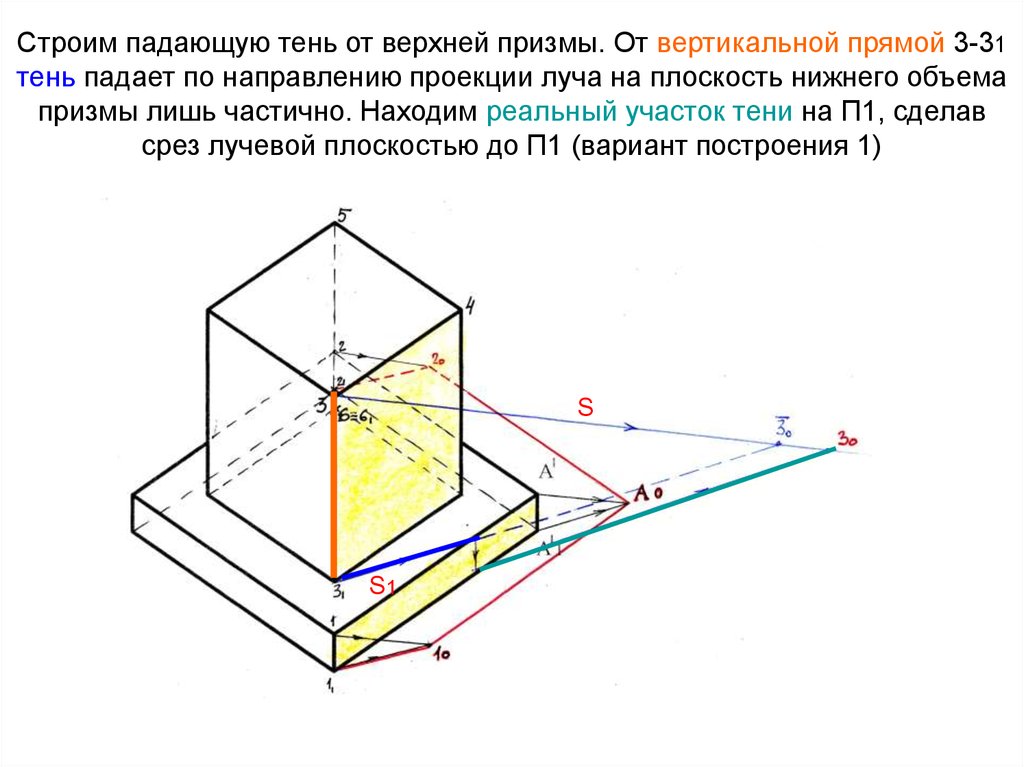
12. Строим падающую тень от верхней призмы. От вертикальной прямой 3-31 тень падает по направлению проекции луча на плоскость
нижнего объемапризмы лишь частично. Находим реальный участок тени на П1, сделав
срез лучевой плоскостью до П1 (вариант построения 1)
S
S1
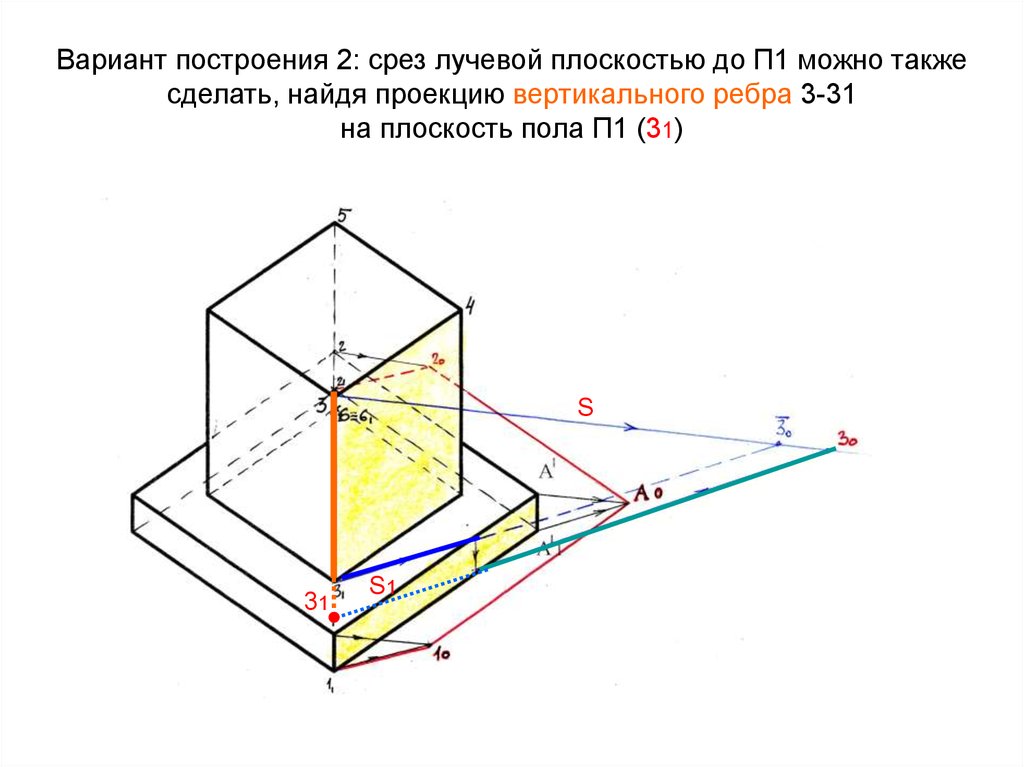
13. Вариант построения 2: срез лучевой плоскостью до П1 можно также сделать, найдя проекцию вертикального ребра 3-31 на плоскость
пола П1 (31)S
31
S1
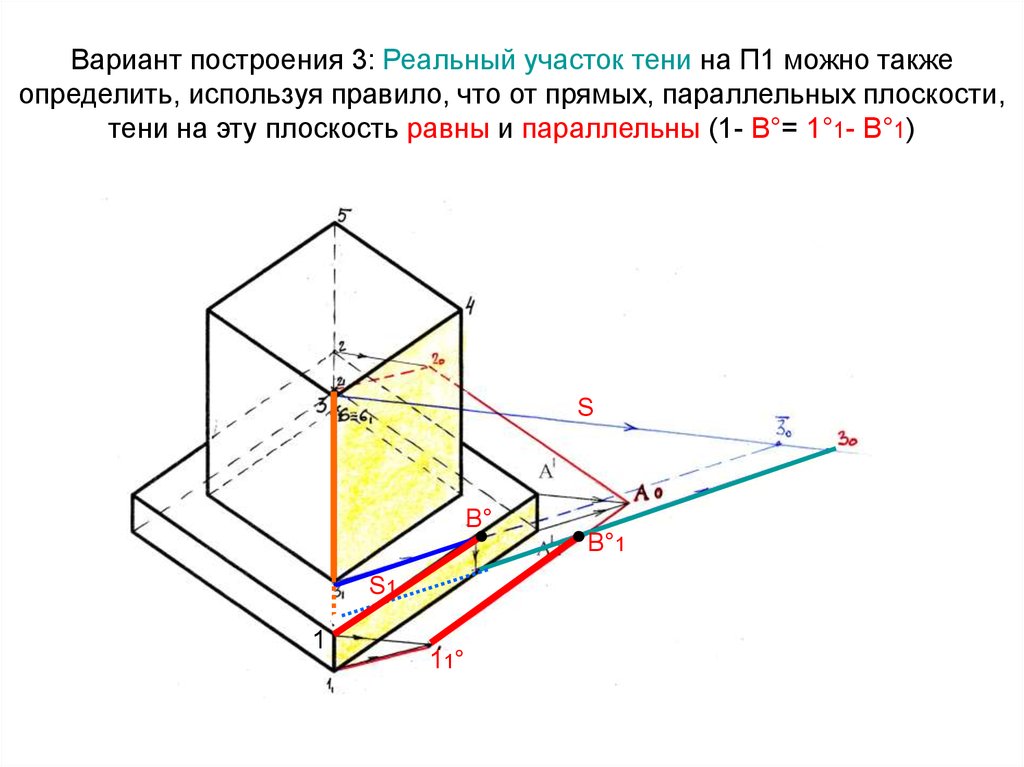
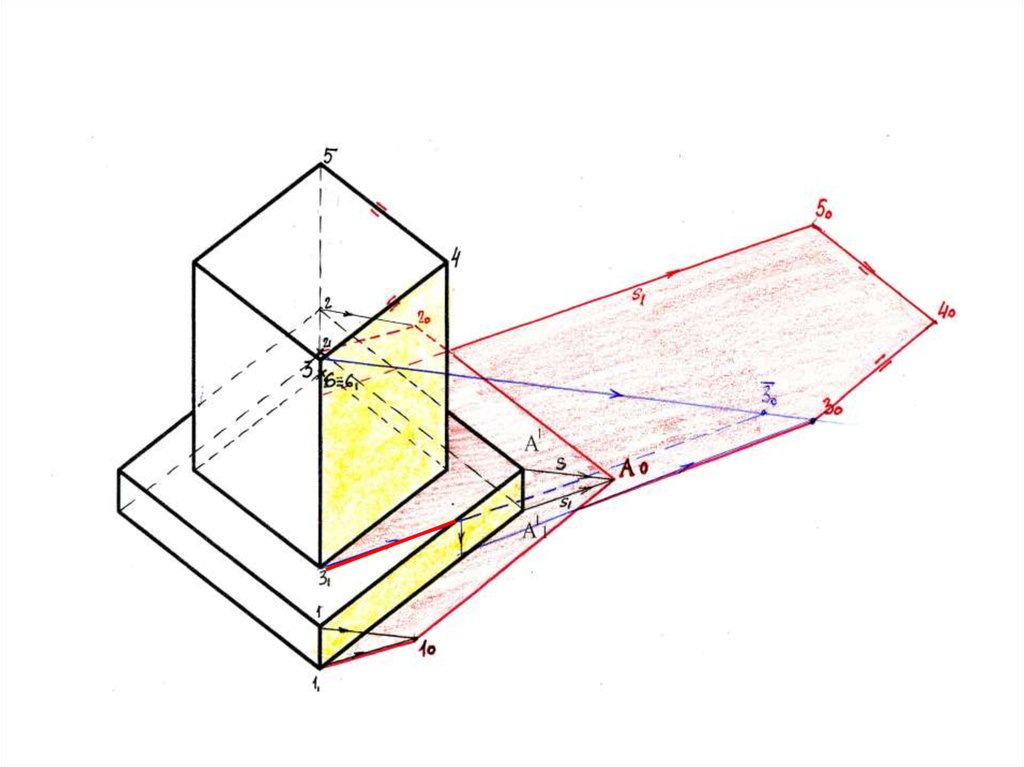
14. Вариант построения 3: Реальный участок тени на П1 можно также определить, используя правило, что от прямых, параллельных
плоскости,тени на эту плоскость равны и параллельны (1- В°= 1°1- В°1)
S
В°
S1
1
11°
●В°1
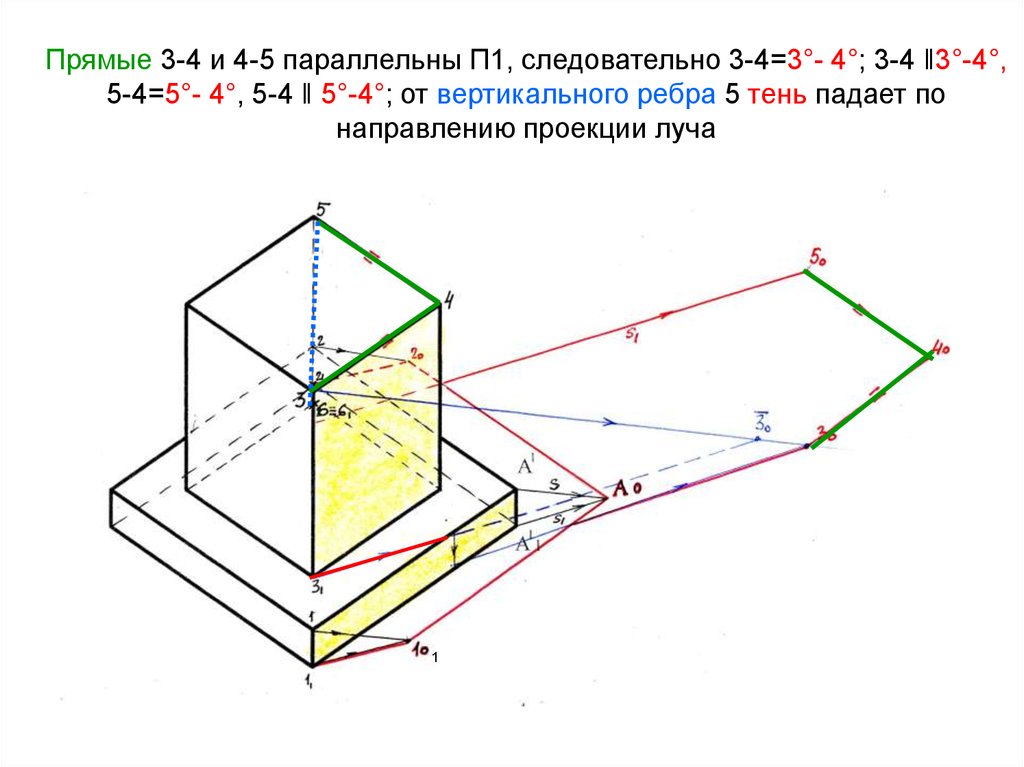
15. Прямые 3-4 и 4-5 параллельны П1, следовательно 3-4=3°- 4°; 3-4 ‖3°-4°, 5-4=5°- 4°, 5-4 ‖ 5°-4°; от вертикального ребра 5 тень
падает понаправлению проекции луча
1
16.
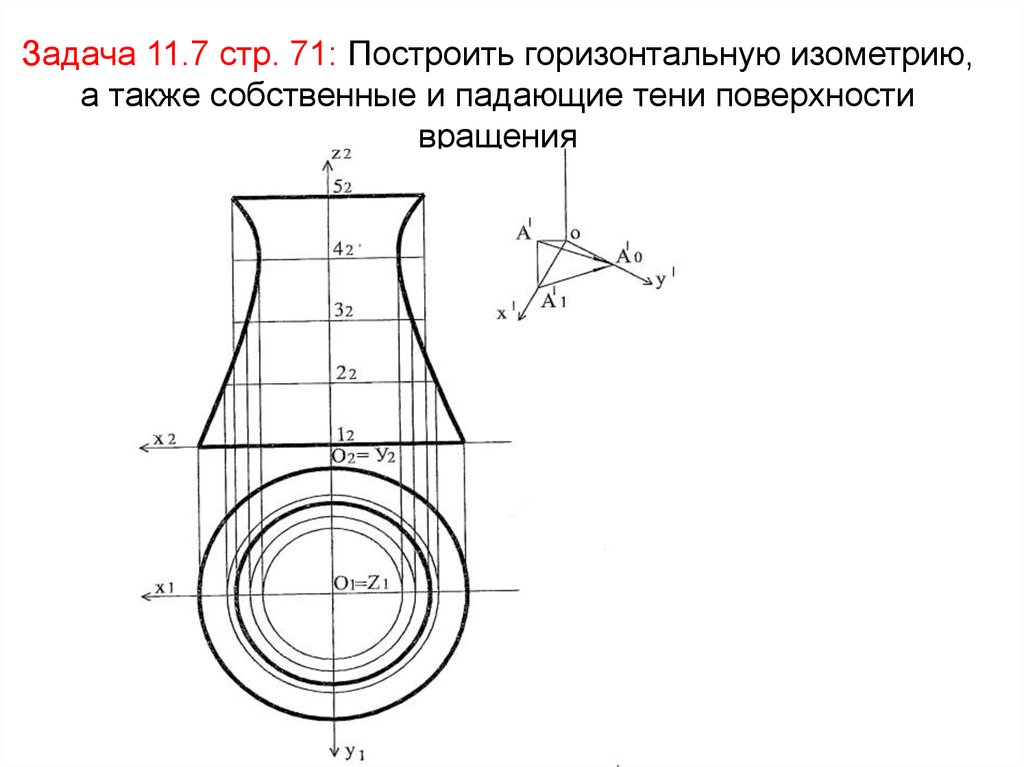
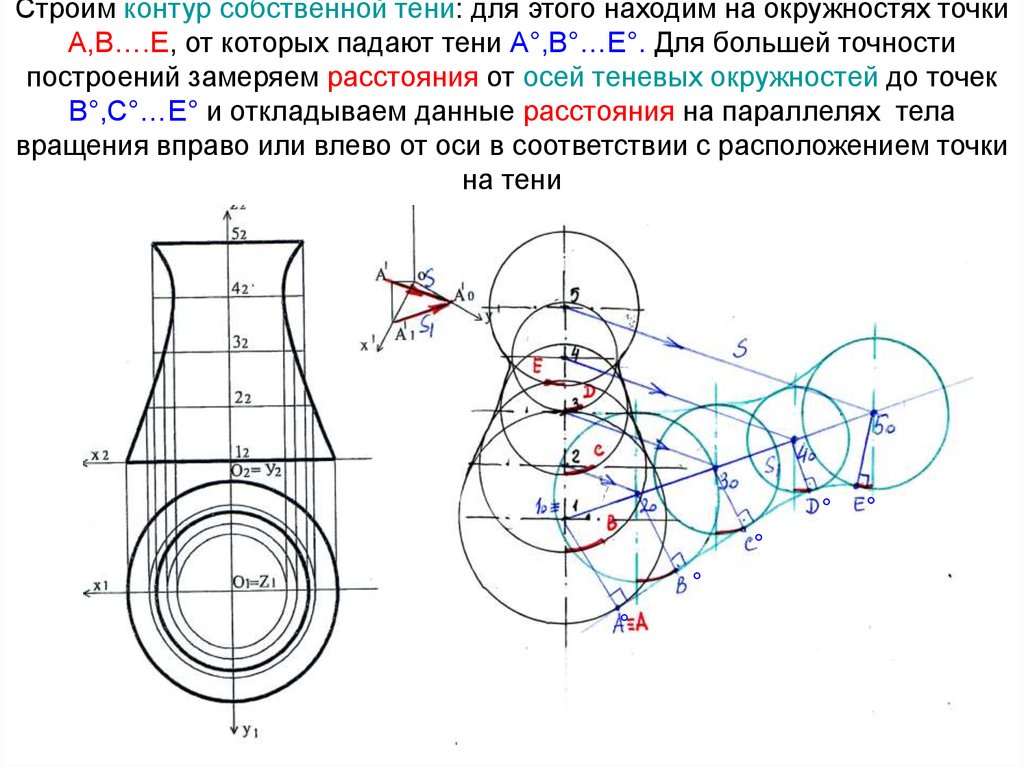
17. Задача 11.7 стр. 71: Построить горизонтальную изометрию, а также собственные и падающие тени поверхности вращения
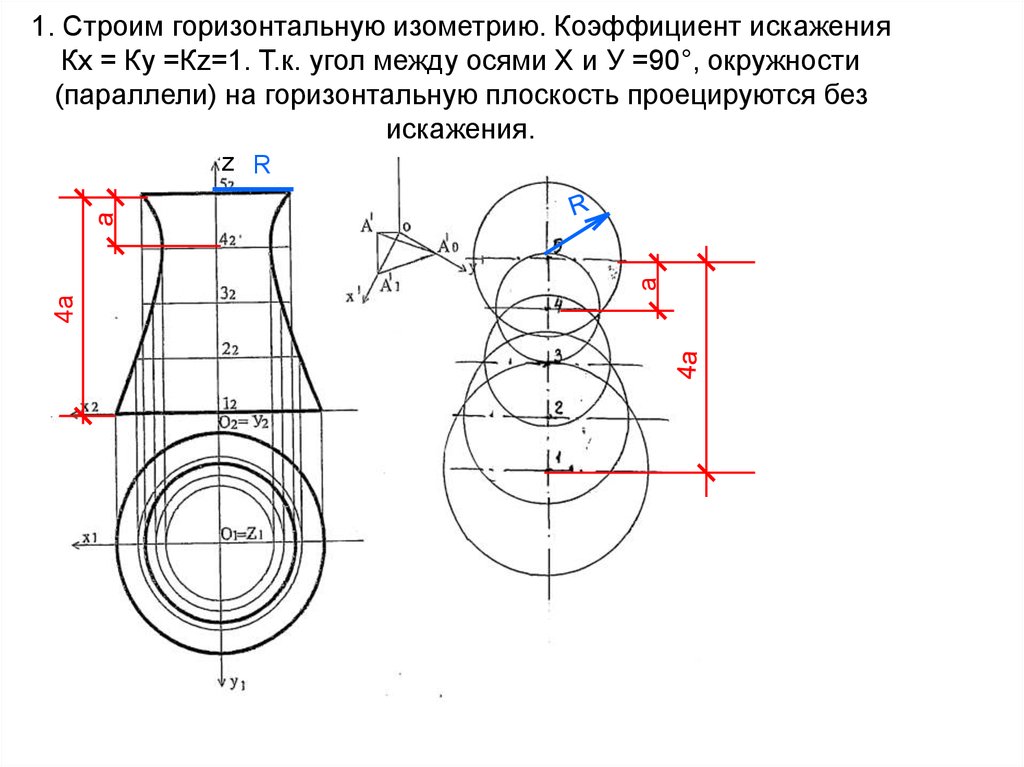
18. 1. Строим горизонтальную изометрию. Коэффициент искажения Кх = Ку =Кz=1. Т.к. угол между осями Х и У =90°, окружности
(параллели) на горизонтальную плоскость проецируются безискажения.
4a
a
z R
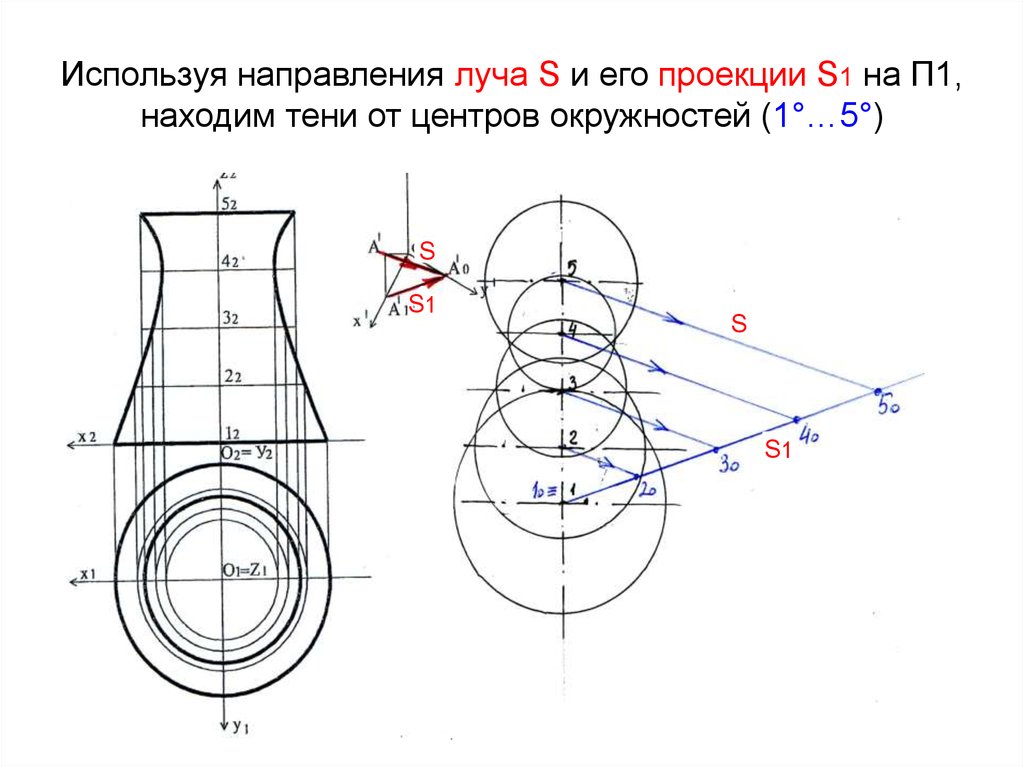
19. Используя направления луча S и его проекции S1 на П1, находим тени от центров окружностей (1°…5°)
SS1
S
S1
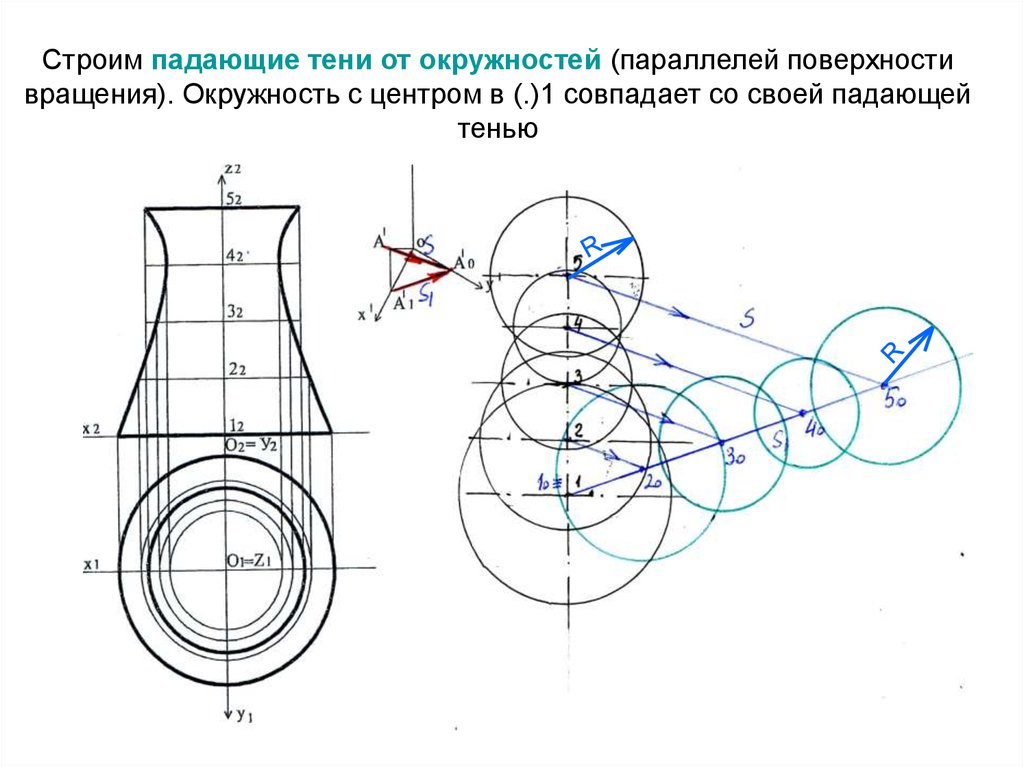
20. Строим падающие тени от окружностей (параллелей поверхности вращения). Окружность с центром в (.)1 совпадает со своей падающей
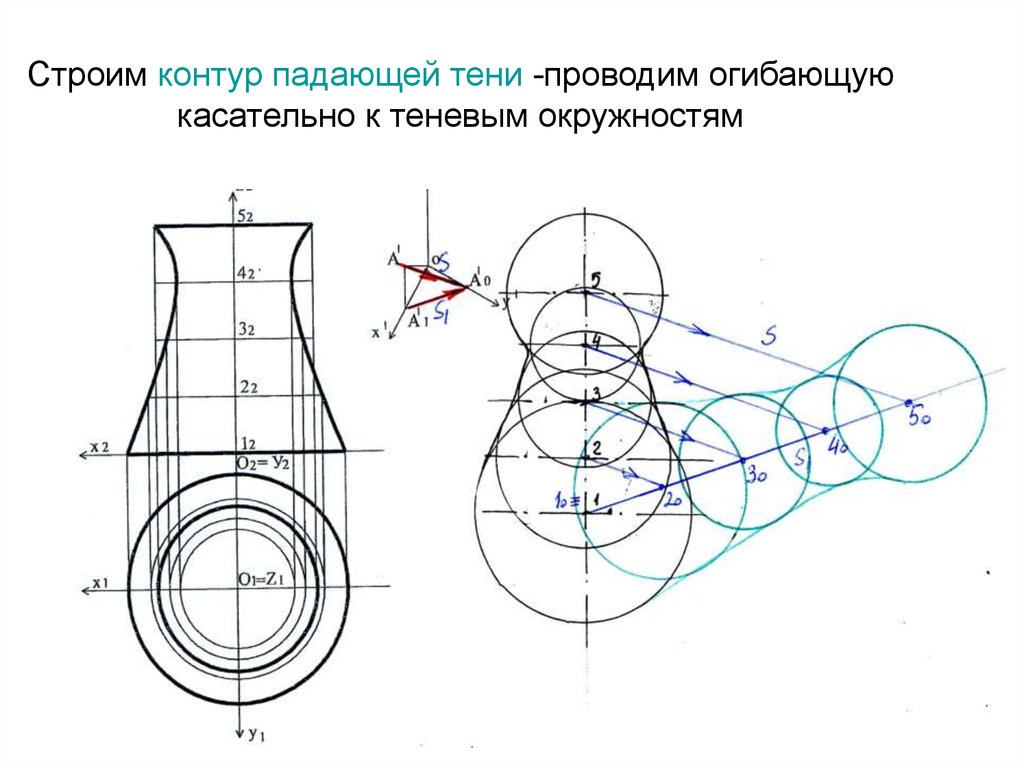
тенью21. Строим контур падающей тени -проводим огибающую касательно к теневым окружностям
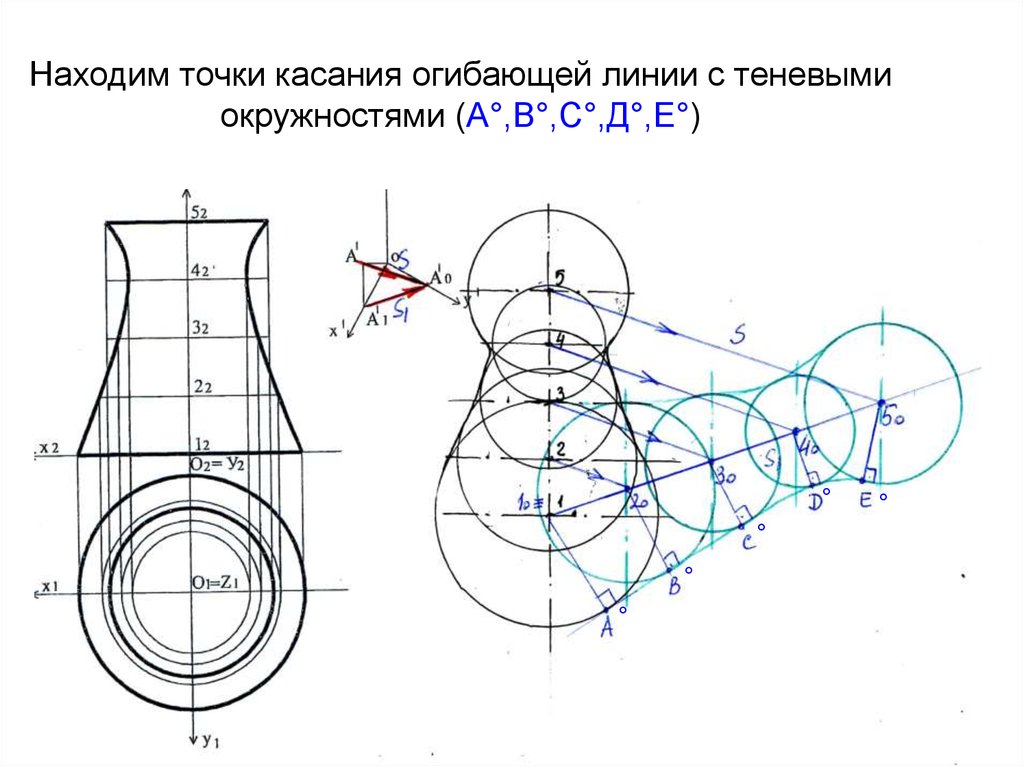
22. Находим точки касания огибающей линии с теневыми окружностями (А°,В°,С°,Д°,Е°)
°°
°
°
°
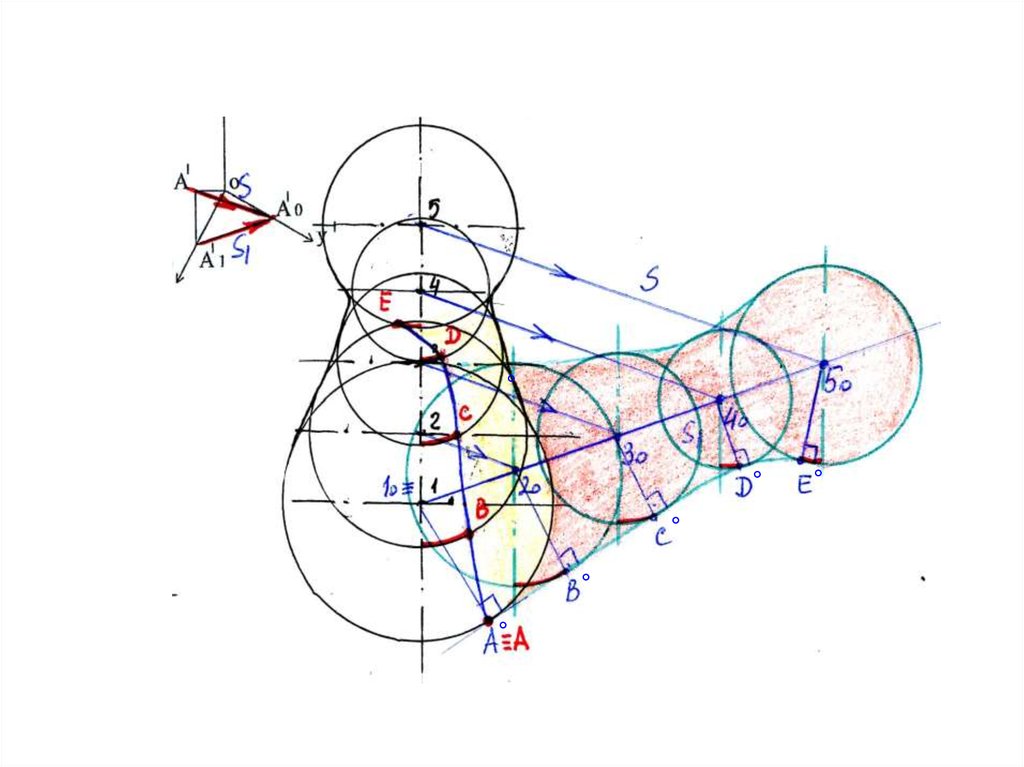
23. Строим контур собственной тени: для этого находим на окружностях точки А,В….Е, от которых падают тени А°,В°…Е°. Для большей
точностипостроений замеряем расстояния от осей теневых окружностей до точек
В°,С°…Е° и откладываем данные расстояния на параллелях тела
вращения вправо или влево от оси в соответствии с расположением точки
на тени
°
°
°
°
°
24.
°°
°
°
°
°
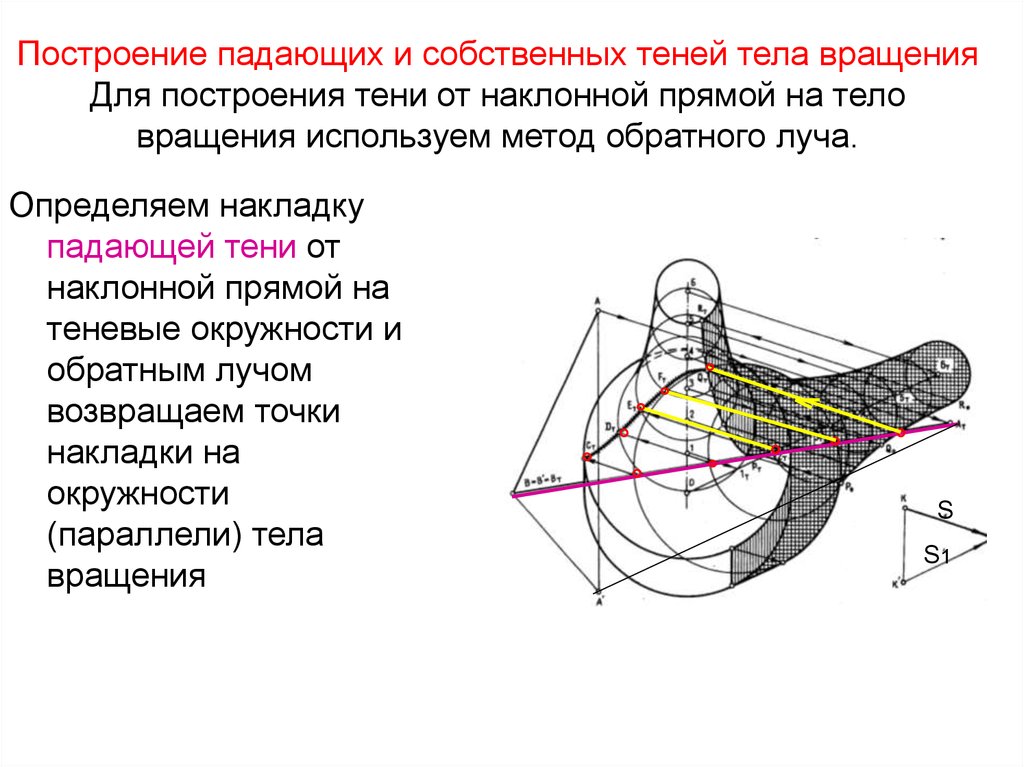
25. Построение падающих и собственных теней тела вращения Для построения тени от наклонной прямой на тело вращения используем метод
обратного луча.Определяем накладку
падающей тени от
наклонной прямой на
теневые окружности и
обратным лучом
возвращаем точки
накладки на
окружности
(параллели) тела
вращения
°
°
°
°
°
°
°
°
°
°
S
S1
26.
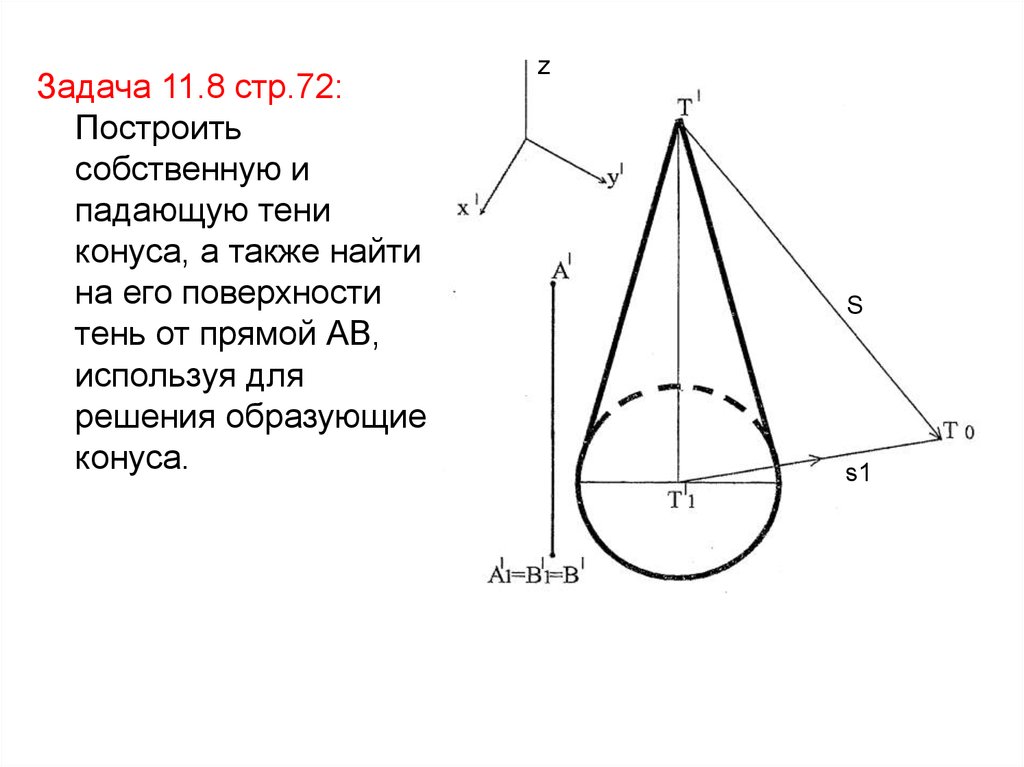
Задача 11.8 стр.72:Построить
собственную и
падающую тени
конуса, а также найти
на его поверхности
тень от прямой АВ,
используя для
решения образующие
конуса.
z
S
s1
27.
S21
S1
11
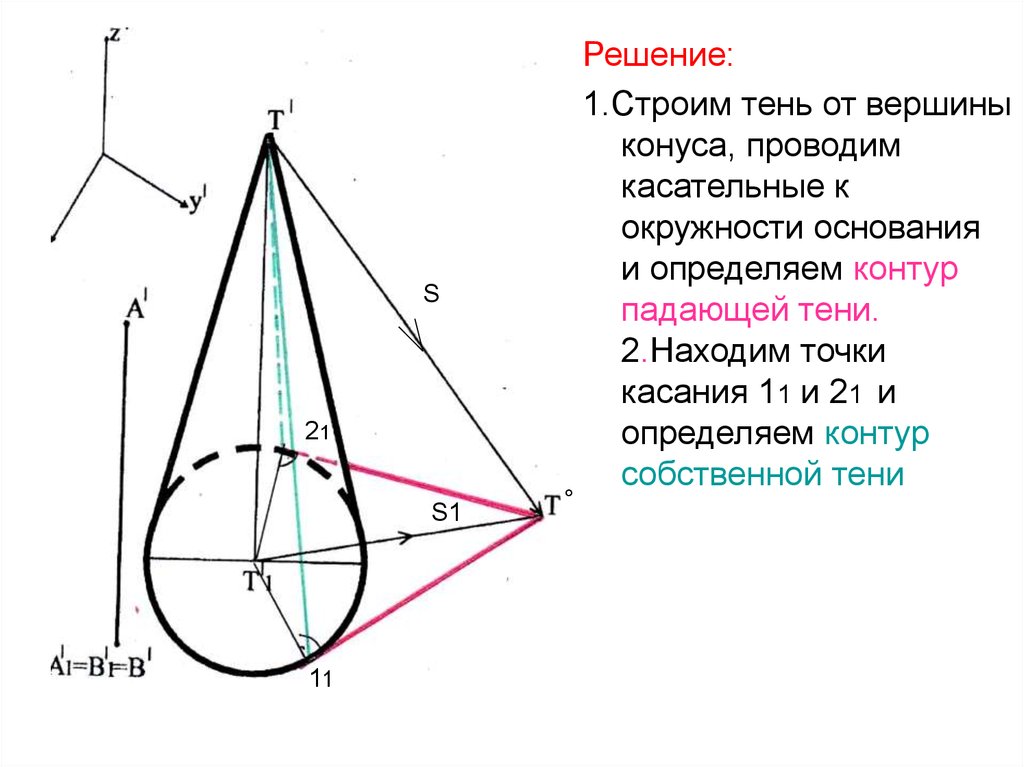
°
Решение:
1.Строим тень от вершины
конуса, проводим
касательные к
окружности основания
и определяем контур
падающей тени.
2.Находим точки
касания 11 и 21 и
определяем контур
собственной тени
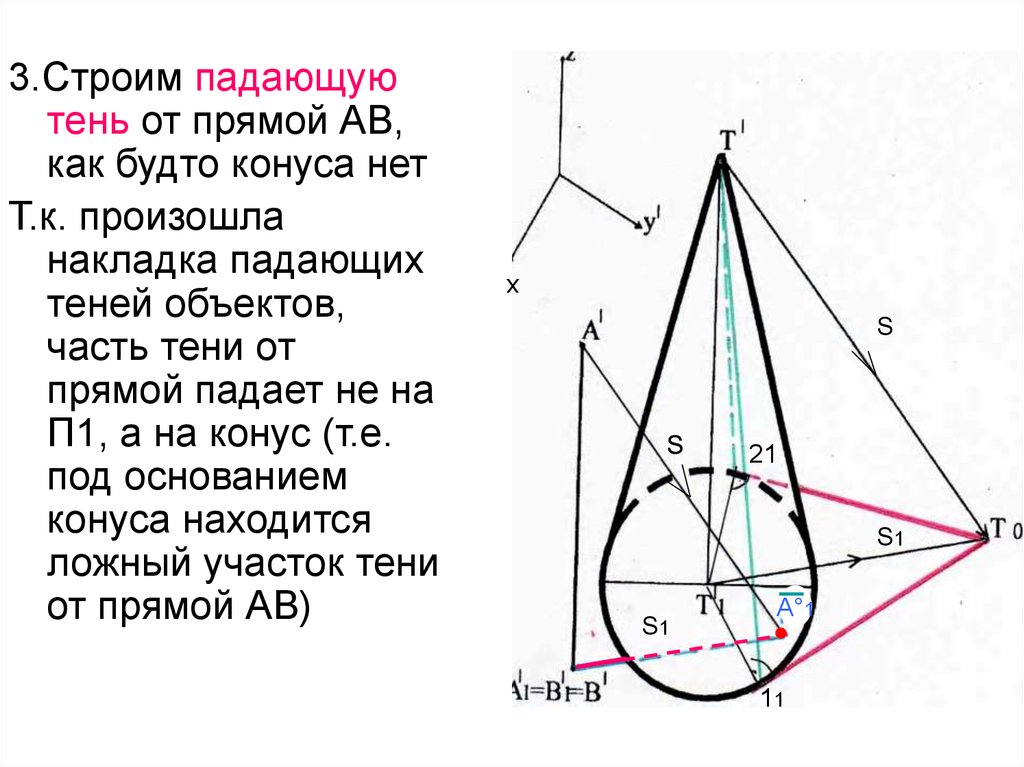
28.
3.Строим падающуютень от прямой АВ,
как будто конуса нет
Т.к. произошла
накладка падающих
теней объектов,
часть тени от
прямой падает не на
П1, а на конус (т.е.
под основанием
конуса находится
ложный участок тени
от прямой АВ)
х
S
21
S1
S1
А°1
11
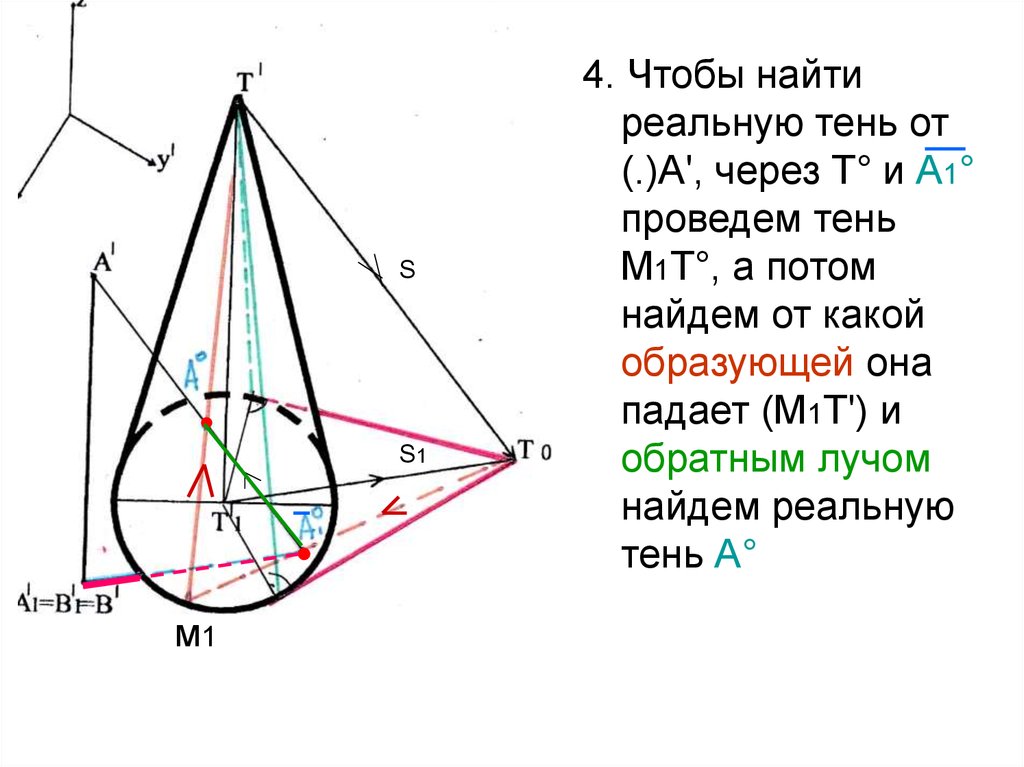
29.
SS1
м1
4. Чтобы найти
реальную тень от
(.)А', через Т° и А1°
проведем тень
М1Т°, а потом
найдем от какой
образующей она
падает (М1Т') и
обратным лучом
найдем реальную
тень А°
30.
SS1
°
C1
1°1
м1
°
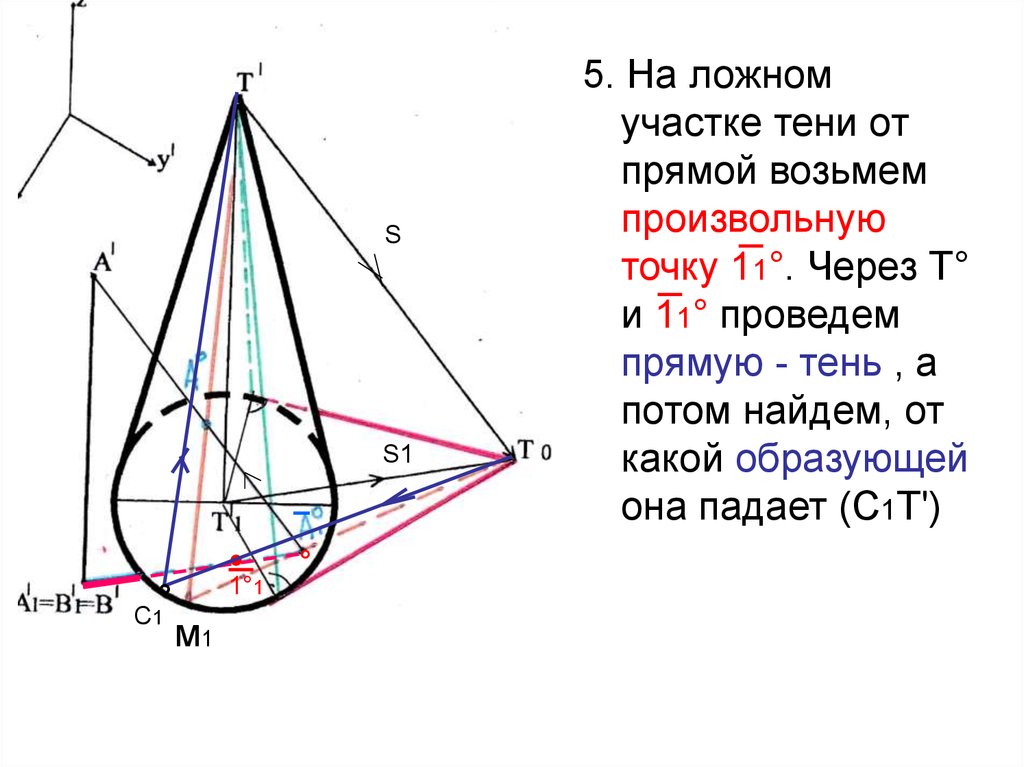
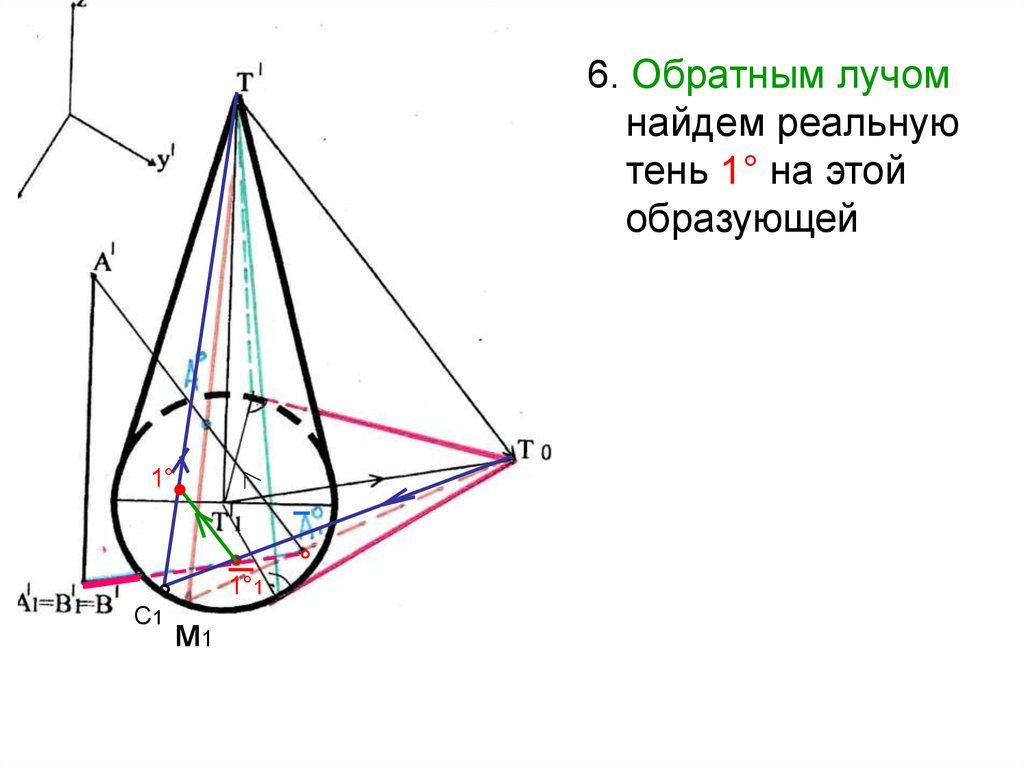
5. На ложном
участке тени от
прямой возьмем
произвольную
точку 11°. Через Т°
и 11° проведем
прямую - тень , а
потом найдем, от
какой образующей
она падает (С1Т')
31.
6. Обратным лучомнайдем реальную
тень 1° на этой
образующей
1°
°
C1
1°1
м1
°
32.
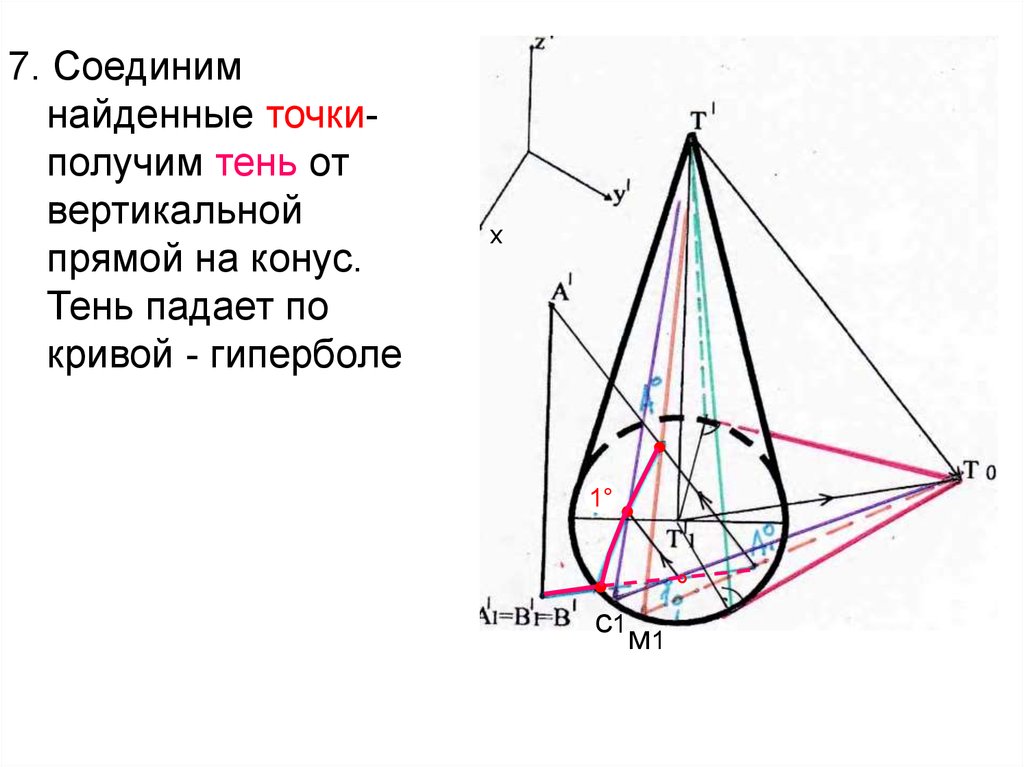
7. Соединимнайденные точкиполучим тень от
вертикальной
прямой на конус.
Тень падает по
кривой - гиперболе
х
1°
с1 м1
°
33.
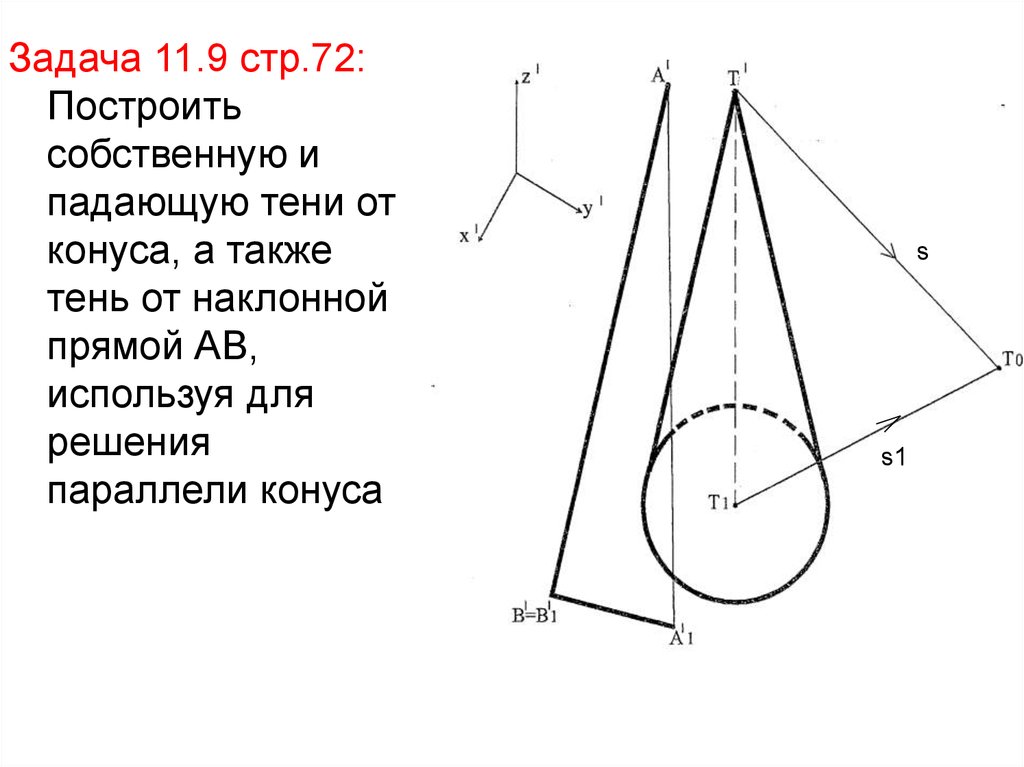
Задача 11.9 стр.72:Построить
собственную и
падающую тени от
конуса, а также
тень от наклонной
прямой АВ,
используя для
решения
параллели конуса
s
s1
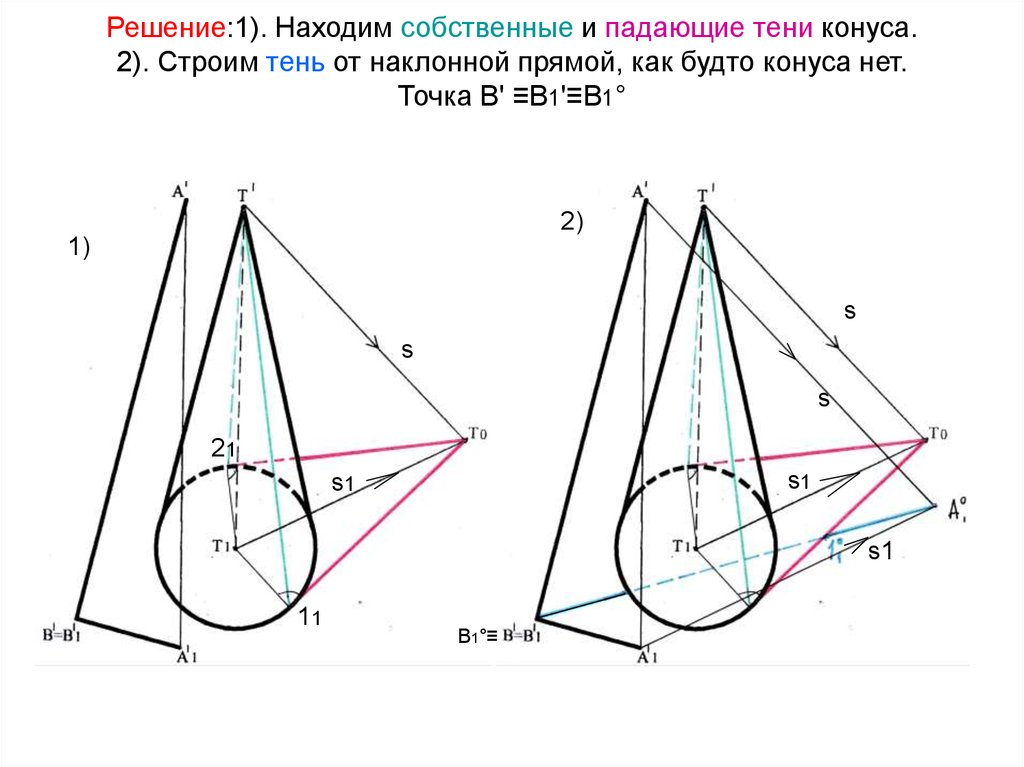
34. Решение:1). Находим собственные и падающие тени конуса. 2). Строим тень от наклонной прямой, как будто конуса нет. Точка В'
≡В1'≡В1°2)
1)
s
s
s
21
s1
s1
s1
11
В1°≡
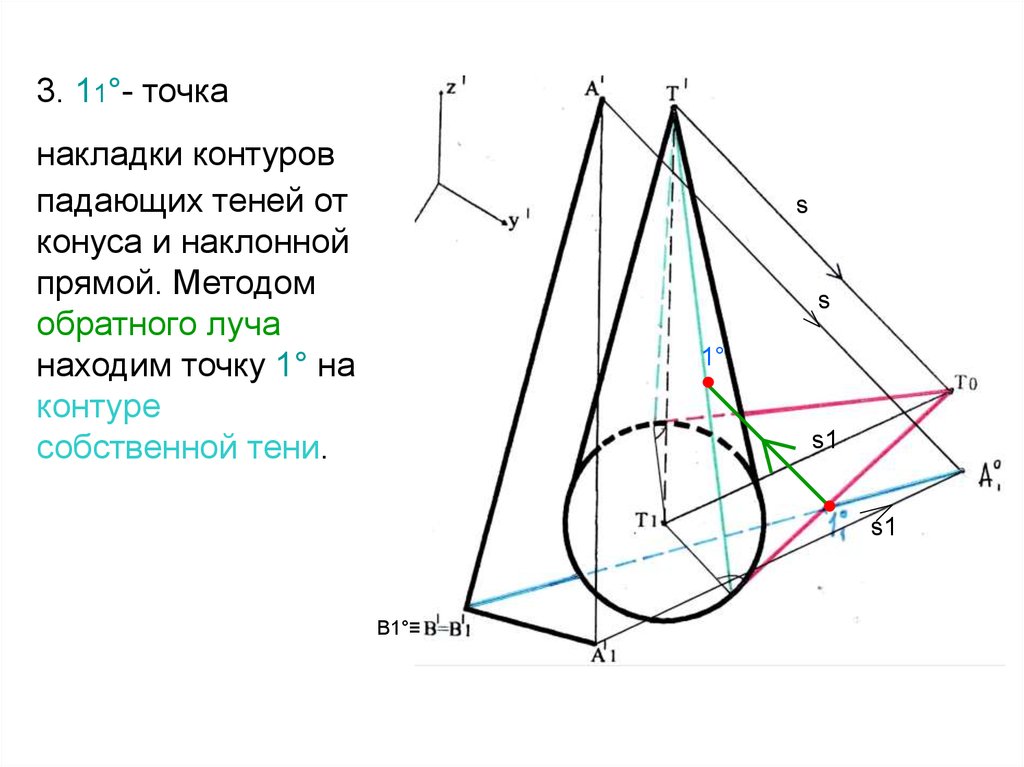
35. 3. 11°- точка накладки контуров падающих теней от конуса и наклонной прямой. Методом обратного луча находим точку 1° на контуре
собственной тени.s
s
1°
s1
В1°≡
s1
36.
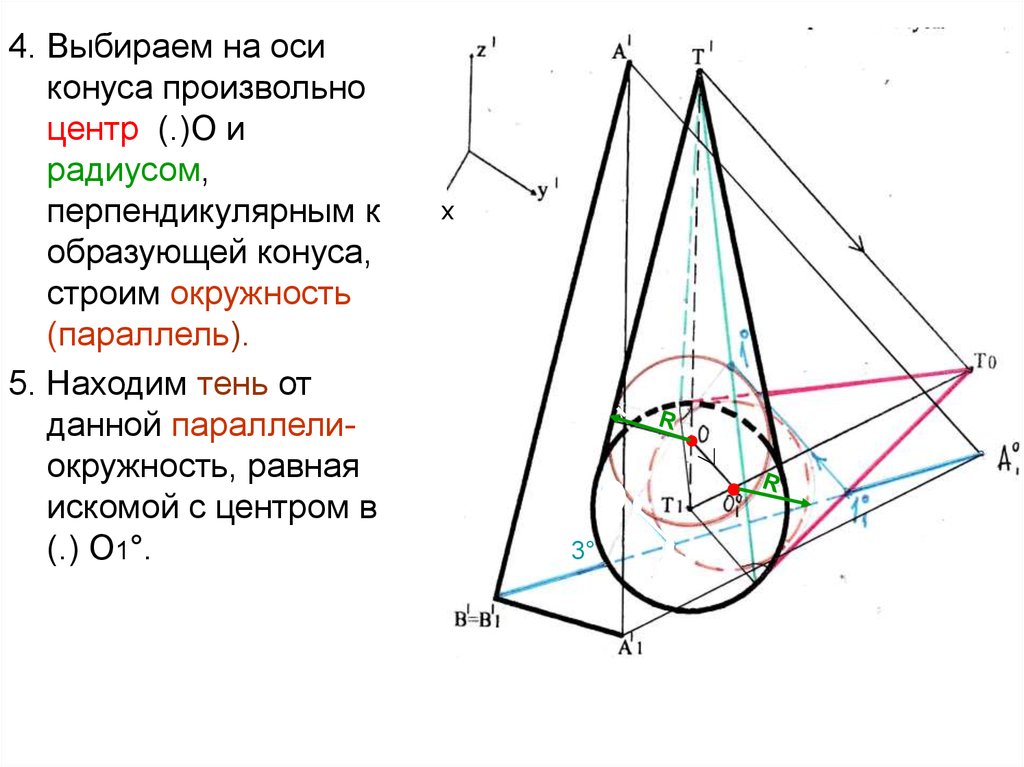
4. Выбираем на осиконуса произвольно
центр (.)О и
радиусом,
перпендикулярным к
образующей конуса,
строим окружность
(параллель).
5. Находим тень от
данной параллелиокружность, равная
искомой с центром в
(.) О1°.
х
3°
37.
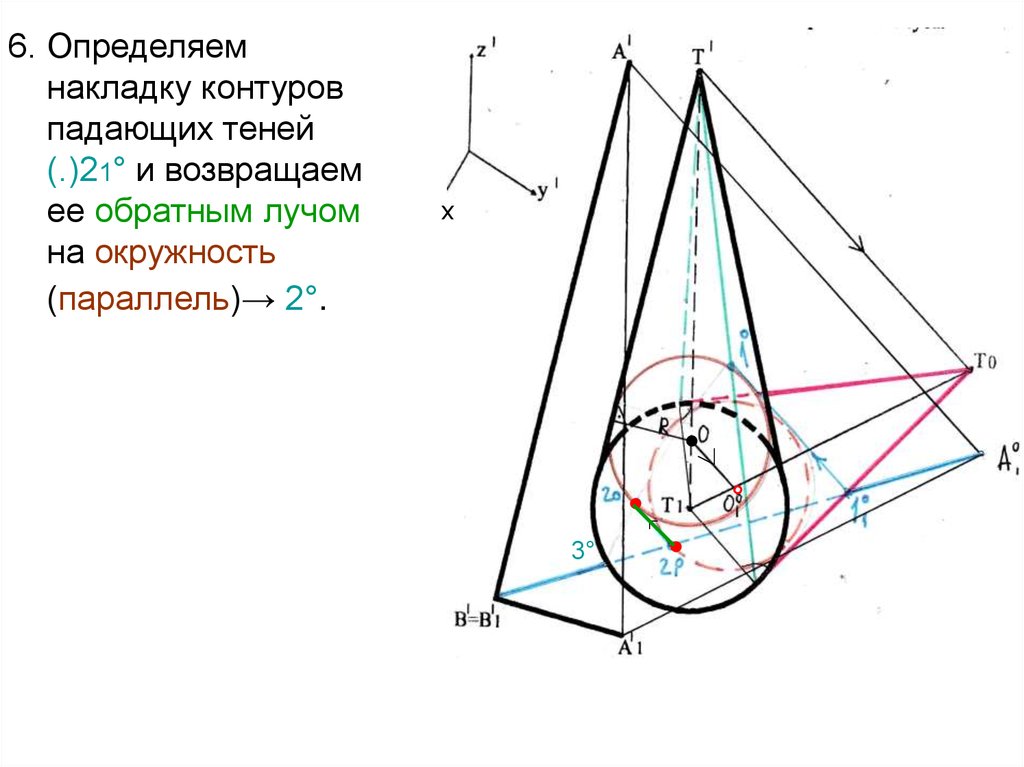
6. Определяемнакладку контуров
падающих теней
(.)21° и возвращаем
ее обратным лучом
на окружность
(параллель)→ 2°.
х
°
3°
38.
7.Завершаемпостроение
падающей тени
от наклонной
прямой на
конус,
соединив
найденные
точки 1°,2°,3°
х
3°
39.
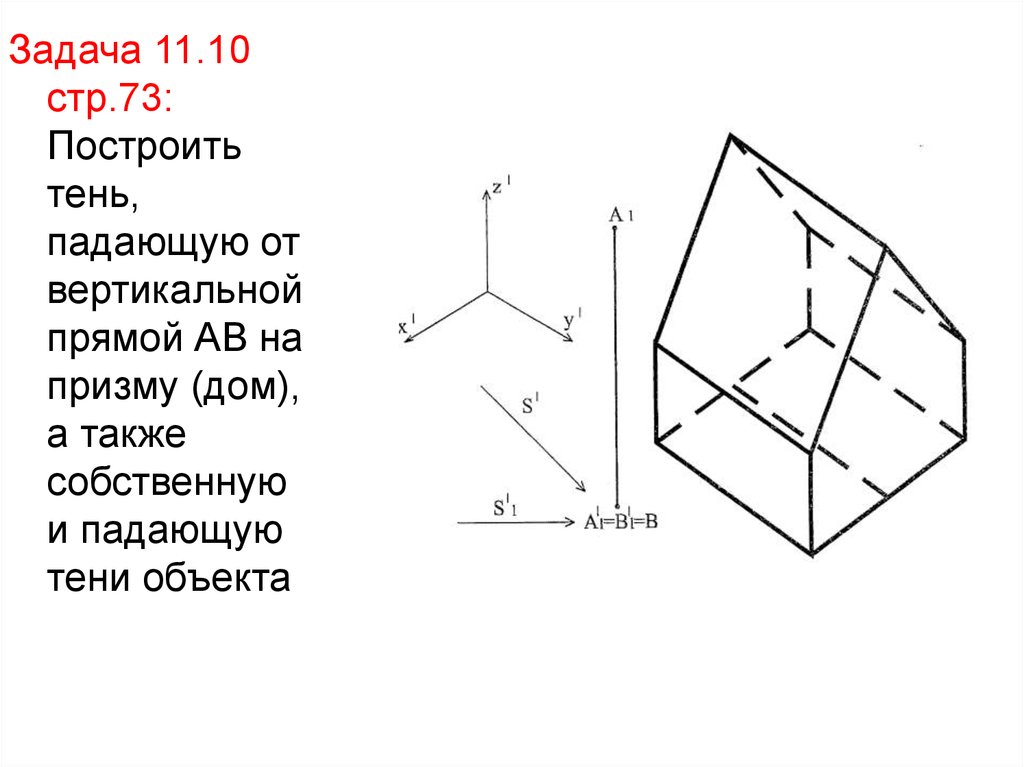
Задача 11.10стр.73:
Построить
тень,
падающую от
вертикальной
прямой АВ на
призму (дом),
а также
собственную
и падающую
тени объекта
40.
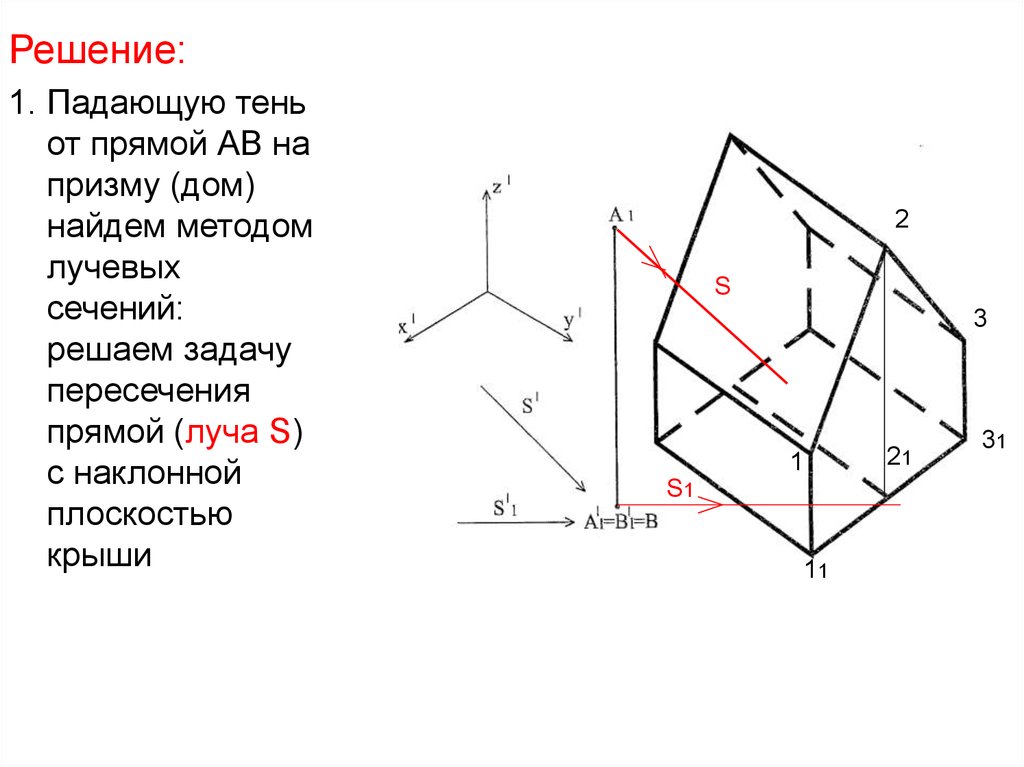
Решение:1. Падающую тень
от прямой АВ на
призму (дом)
найдем методом
лучевых
сечений:
решаем задачу
пересечения
прямой (луча S)
с наклонной
плоскостью
крыши
2
S
3
1
S1
11
21
31
41.
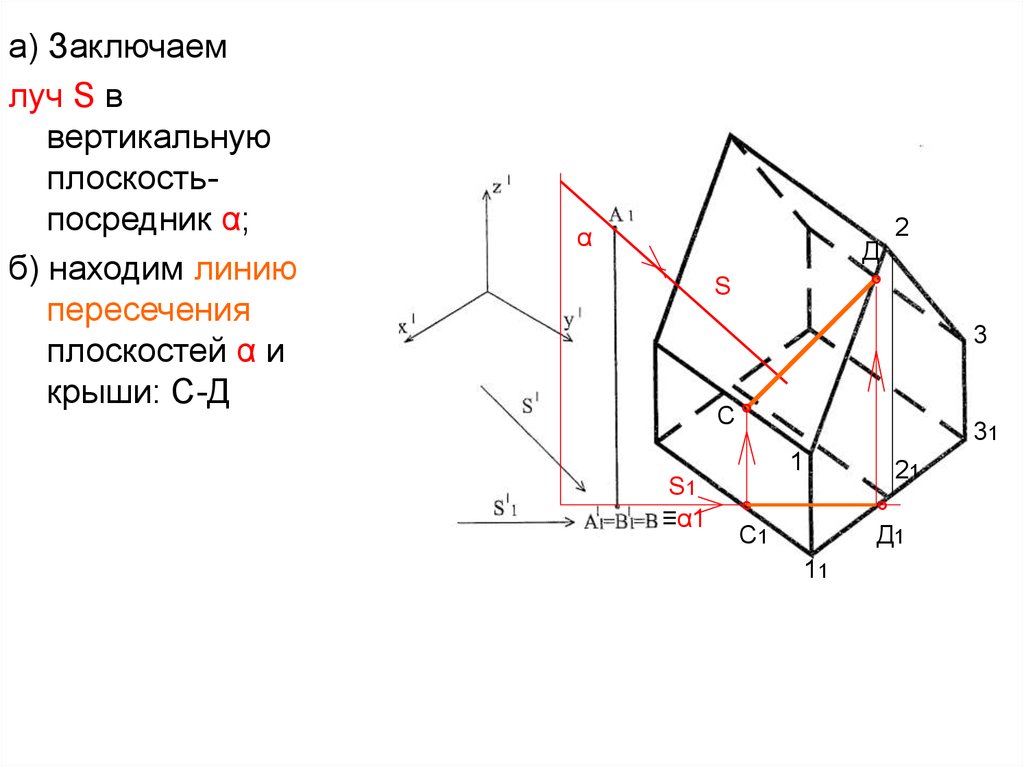
а) Заключаемлуч S в
вертикальную
плоскостьпосредник α;
б) находим линию
пересечения
плоскостей α и
крыши: С-Д
α
Д
2
°
S
3
С°
31
1
S1
≡α1
°
21
°
С1
Д1
11
42.
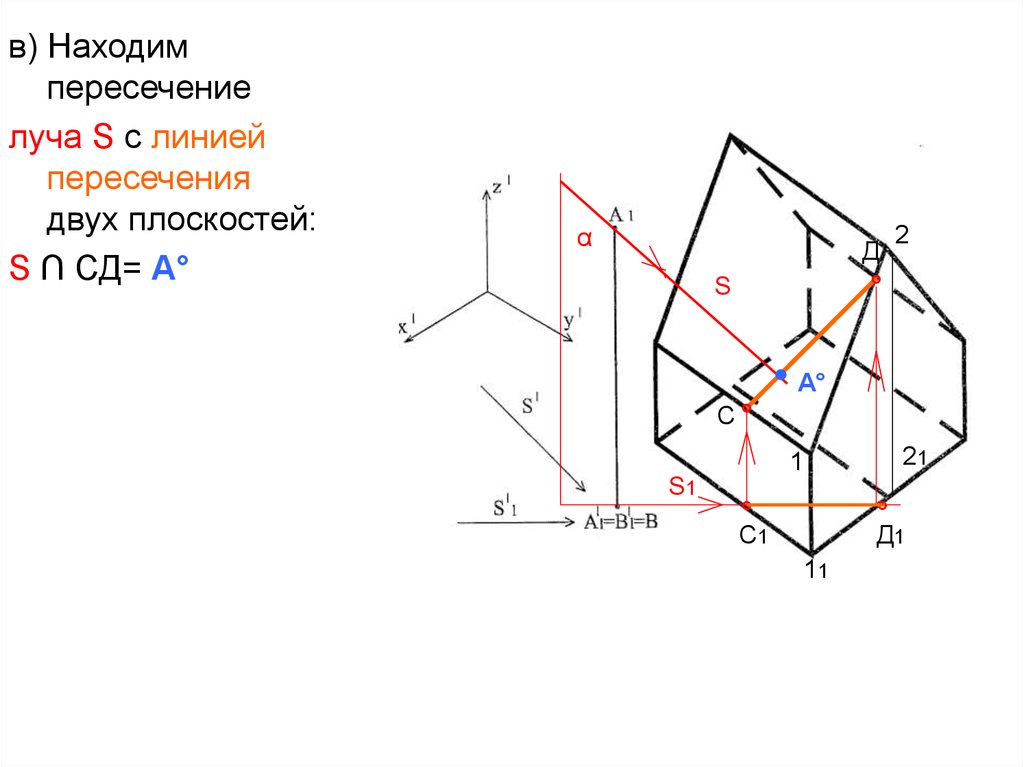
в) Находимпересечение
луча S с линией
пересечения
двух плоскостей:
S ∩ СД= А°
α
Д
2
°
S
● А°
С°
21
1
S1
°
°
С1
Д1
11
43.
г) выделяемреальный
участок тени от
вертикальной
прямой на пол,
стену и крышу
α
Д
2
°
S
3
● А°
С°
21
1
S1
°
°
С1
Д1
11
31
44.
2) Определяемосвещенность
дома:
По направлению луча
S видно, что левая
наклонная
плоскость крыши
освещена.
Освещенность
правой части крыши
не известна (можно
будет определить
только после
построения
падающей тени)
?
S
2
α
Д
°
S
3
● А°
С°
31
1
S1
°
21
°
С1
Д1
11
45.
По направлениюпроекции луча S1
видно, что
вертикальные
левые плоскости
фасадов освещены,
а вертикальные
правые плоскости
фасадов - нет
Угол отклонения
лучевой плоскости
2
α
Д
S
°
S1
● А°
S1
С°
1
S1
S1
°
С1
Угол отклонения
лучевой
плоскости
21
°
Д1
11 S1
46.
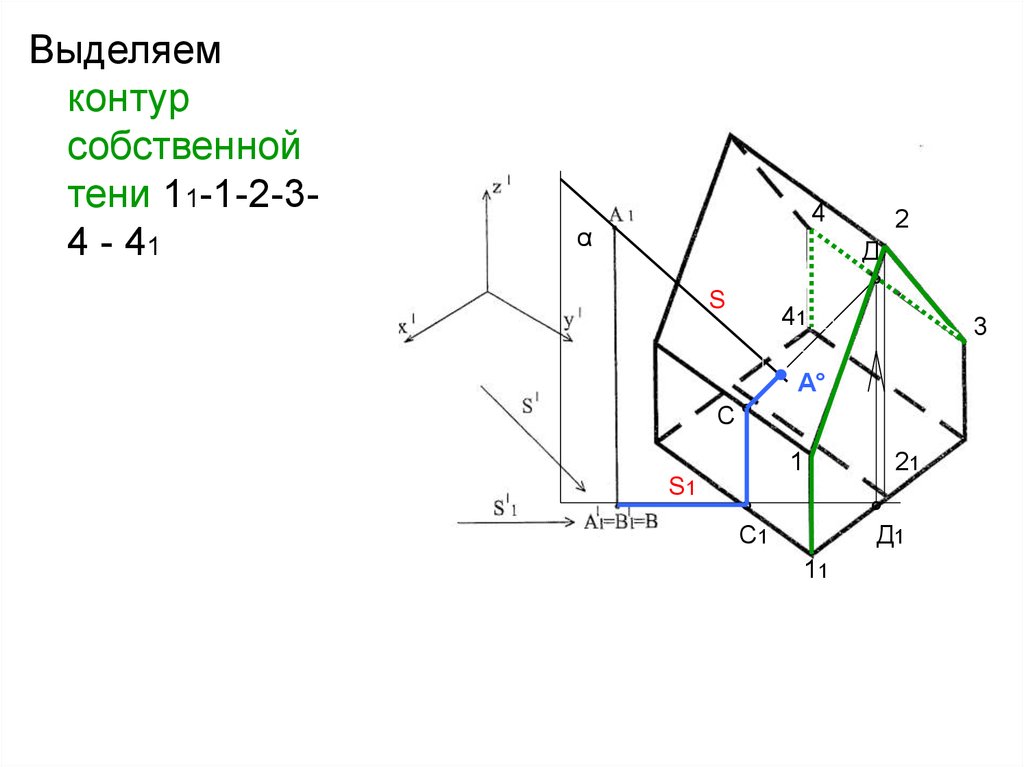
Выделяемконтур
собственной
тени 11-1-2-34 - 41
4
α
2
Д
°
S
41
3
● А°
С°
1
S1
°
21
°
С1
Д1
11
47.
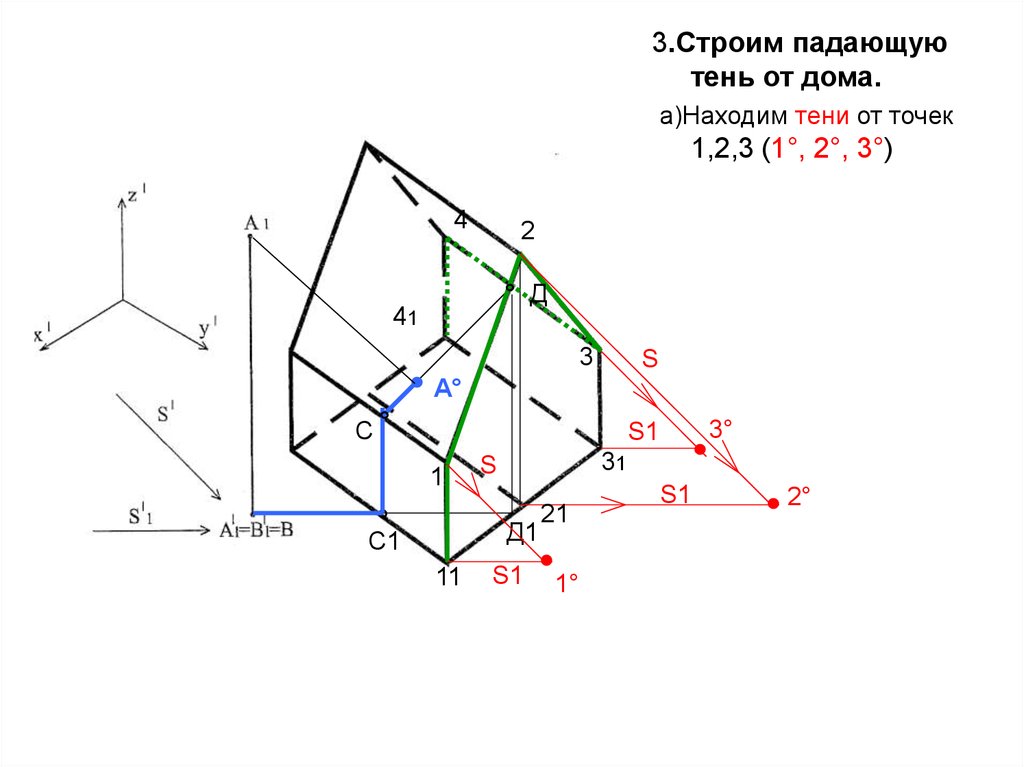
3.Строим падающуютень от дома.
а)Находим тени от точек
1,2,3 (1°, 2°, 3°)
4
2
° Д
41
3
● А°
S
С°
S1
1
°
31
S
Д1
С1
11
S1
21
1°
S1
3°
● 2°
48.
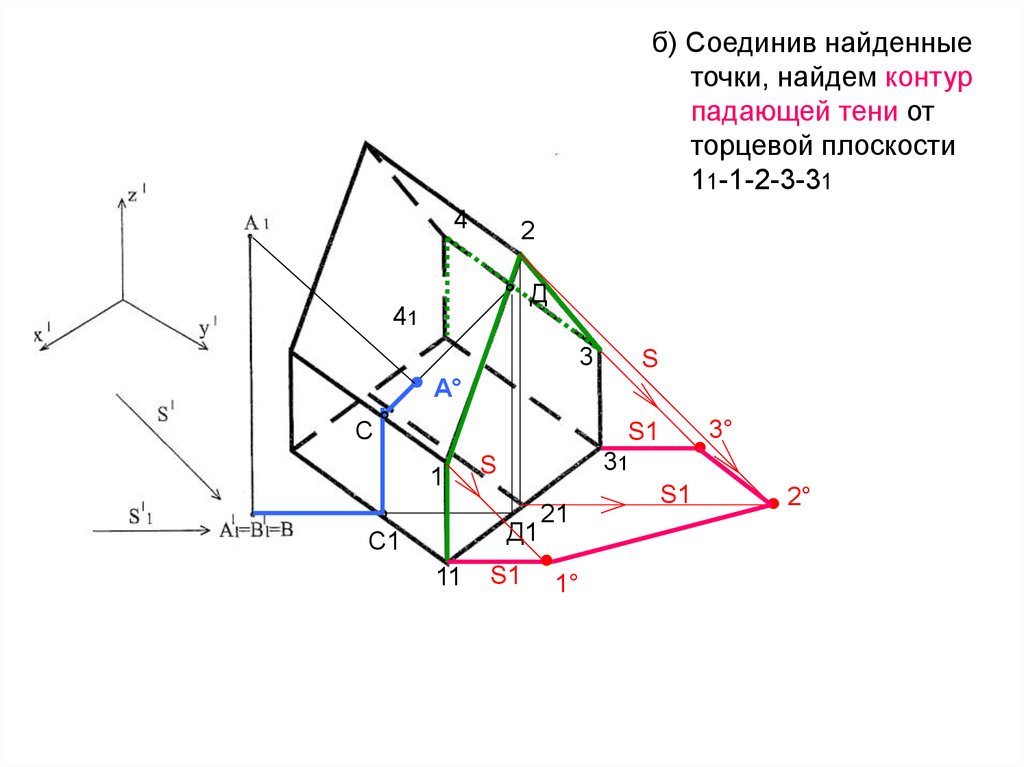
б) Соединив найденныеточки, найдем контур
падающей тени от
торцевой плоскости
11-1-2-3-31
4
2
° Д
41
3
● А°
С°
S
S1
1
°
31
S
Д1
С1
11
S1
21
1°
S1
3°
● 2°
49.
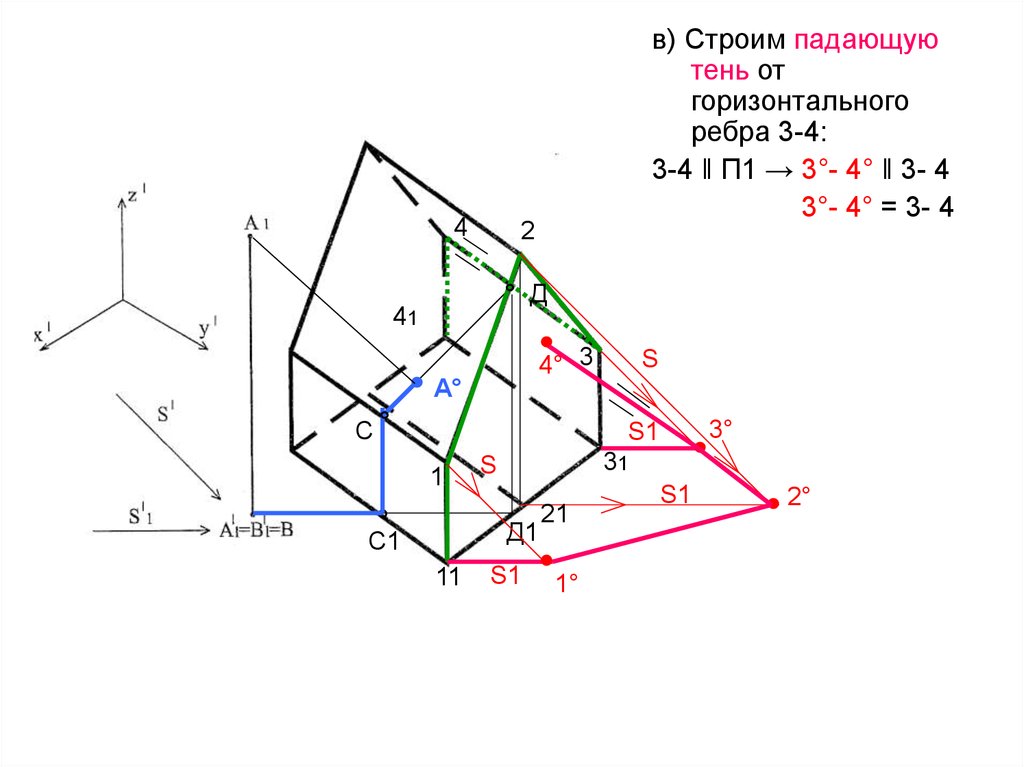
4в) Строим падающую
тень от
горизонтального
ребра 3-4:
3-4 ‖ П1 → 3°- 4° ‖ 3- 4
3°- 4° = 3- 4
2
° Д
41
4° 3
● А°
С°
S
S1
1
°
31
S
Д1
С1
11
S1
21
1°
S1
3°
● 2°
50.
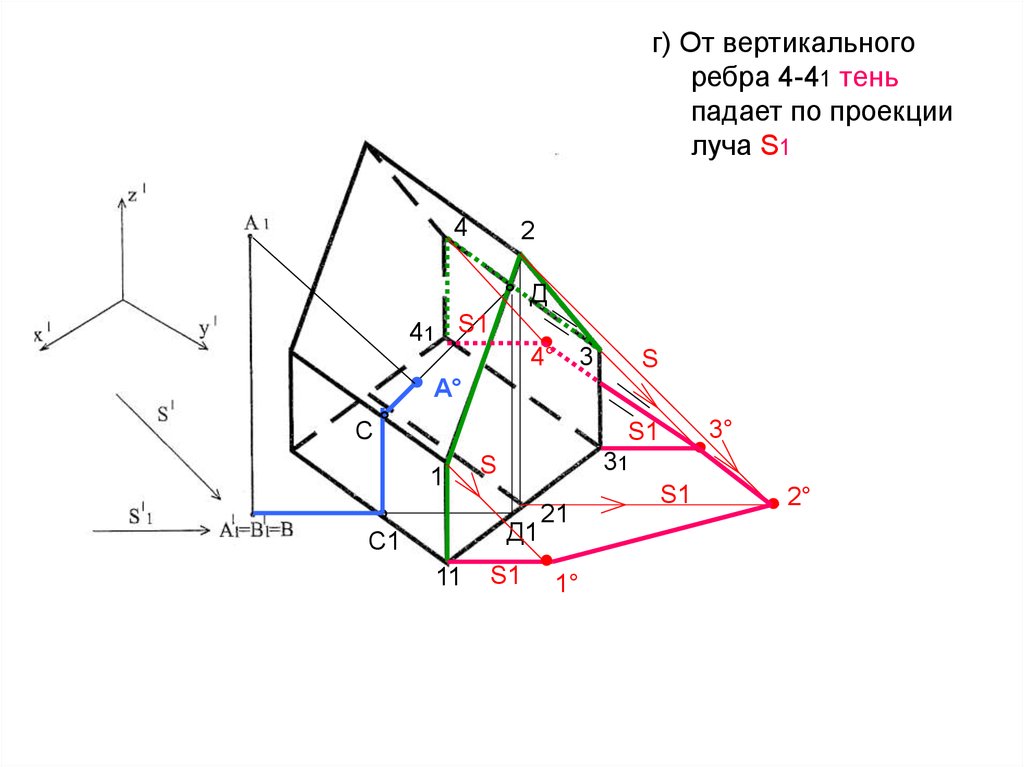
г) От вертикальногоребра 4-41 тень
падает по проекции
луча S1
4
2
° Д
41 S1
4° 3
● А°
С°
S
S1
1
°
31
S
Д1
С1
11
S1
21
1°
S1
3°
● 2°
51.
4) Проверяем, освещена ли вторая наклоннаяплоскость крыши.
Строим тень от конька
(горизонтального ребра
2-2*), параллельного
плоскости П1→ тень на
П1 равна и параллельна
2-2*= 2°-2*°; 2-2*‖ 2°-2*°
2*
4
2
° Д
41 S1
4° 3
● А°
S
2*°
С°
S1
1
°
31
S
Д1
С1
11
S1
21
S1
3°
● 2°
1°
•Т.к.тень от горизонтального ребра 2-2* оказалась внутри тени от объекта,
второй скат кровли тоже освещен. Контур собственной тени проходит по
ребру 3-4 (как и предполагали ранее)
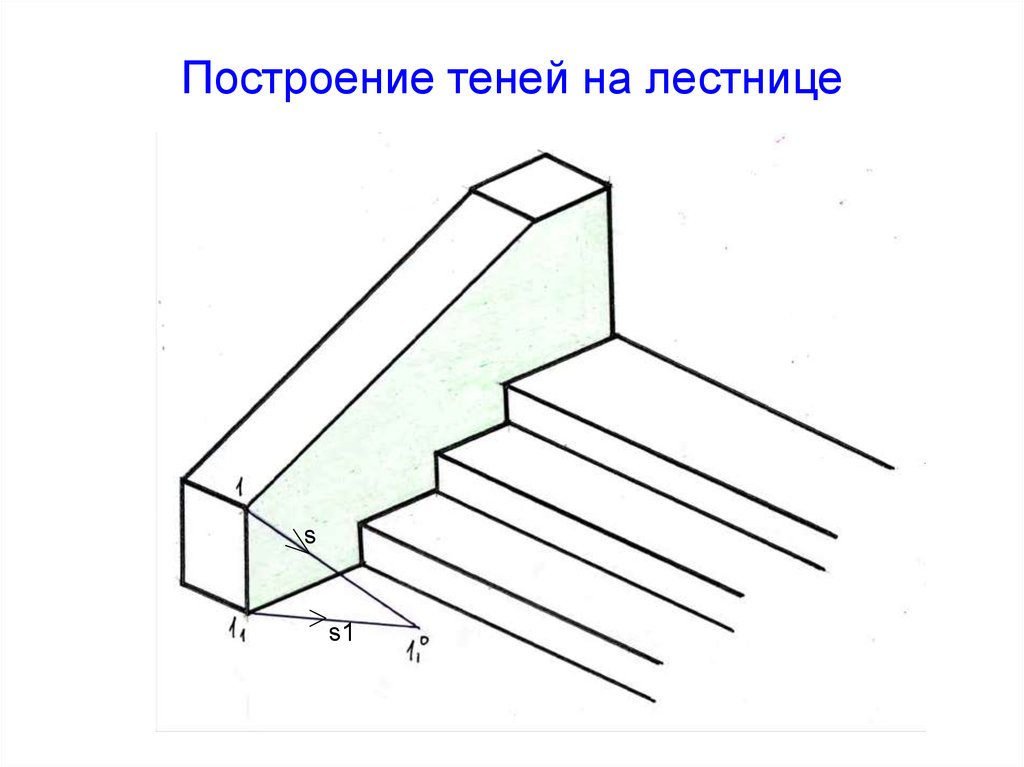
52. Построение теней на лестнице
ss1
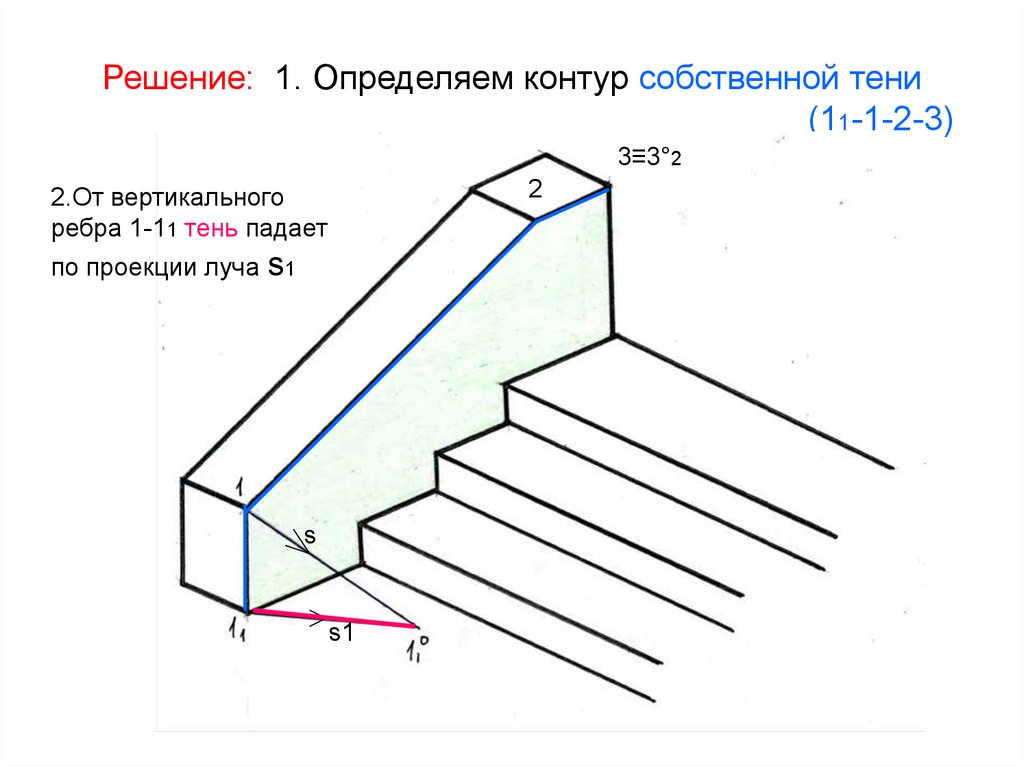
53. Решение: 1. Определяем контур собственной тени (11-1-2-3)
3≡3°22
2.От вертикального
ребра 1-11 тень падает
по проекции луча s1
s
s1
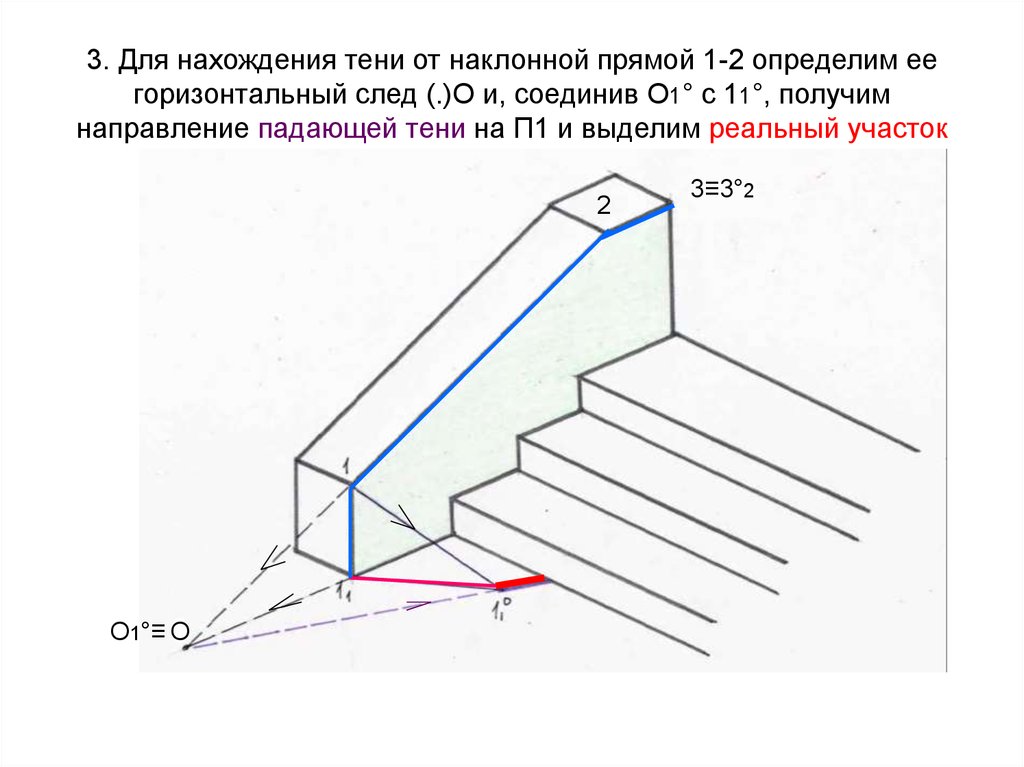
54. 3. Для нахождения тени от наклонной прямой 1-2 определим ее горизонтальный след (.)О и, соединив О1° с 11°, получим направление
падающей тени на П1 и выделим реальный участок2
О1°≡ О
3≡3°2
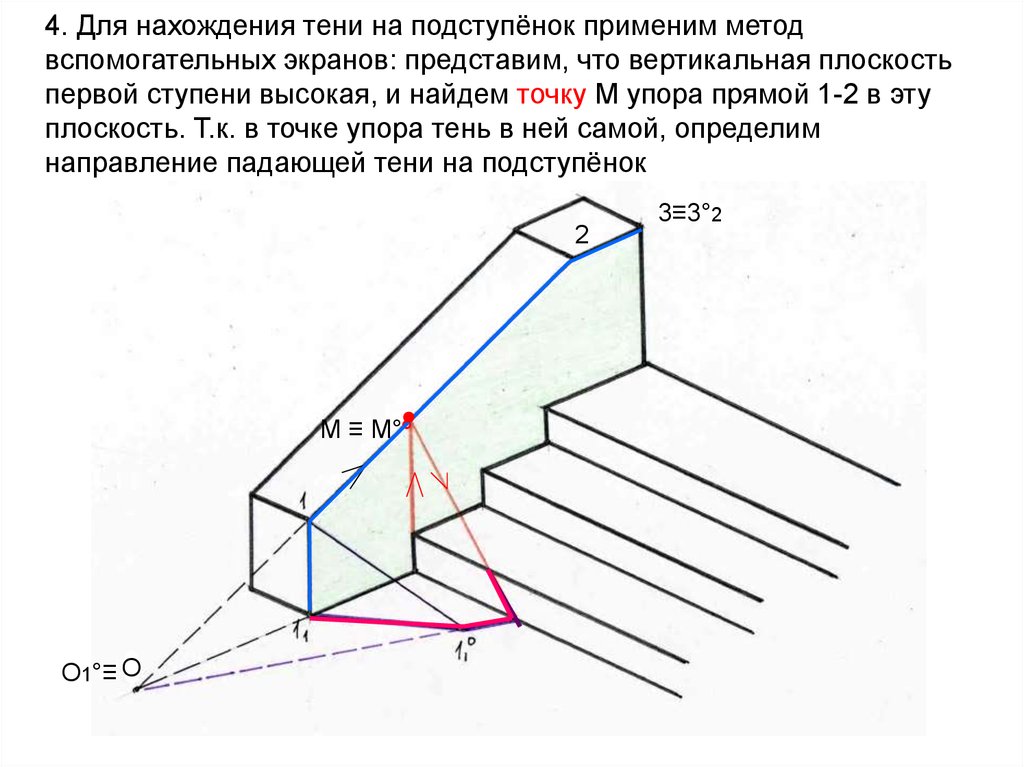
55. 4. Для нахождения тени на подступёнок применим метод вспомогательных экранов: представим, что вертикальная плоскость первой
ступени высокая, и найдем точку М упора прямой 1-2 в этуплоскость. Т.к. в точке упора тень в ней самой, определим
направление падающей тени на подступёнок
2
М ≡ М°°
О1°≡ О
3≡3°2
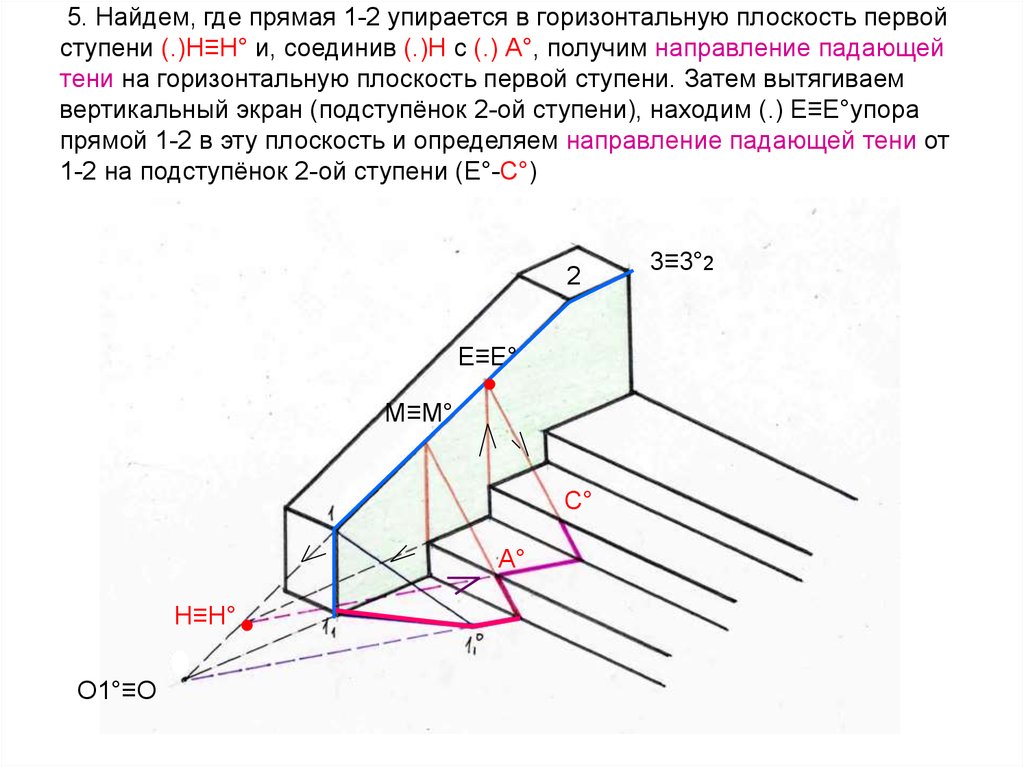
56. 5. Найдем, где прямая 1-2 упирается в горизонтальную плоскость первой ступени (.)Н≡Н° и, соединив (.)Н с (.) А°, получим
направление падающейтени на горизонтальную плоскость первой ступени. Затем вытягиваем
вертикальный экран (подступёнок 2-ой ступени), находим (.) Е≡Е°упора
прямой 1-2 в эту плоскость и определяем направление падающей тени от
1-2 на подступёнок 2-ой ступени (Е°-С°)
2
Е≡Е°
М≡М°
С°
А°
Н≡Н°
О1°≡О
3≡3°2
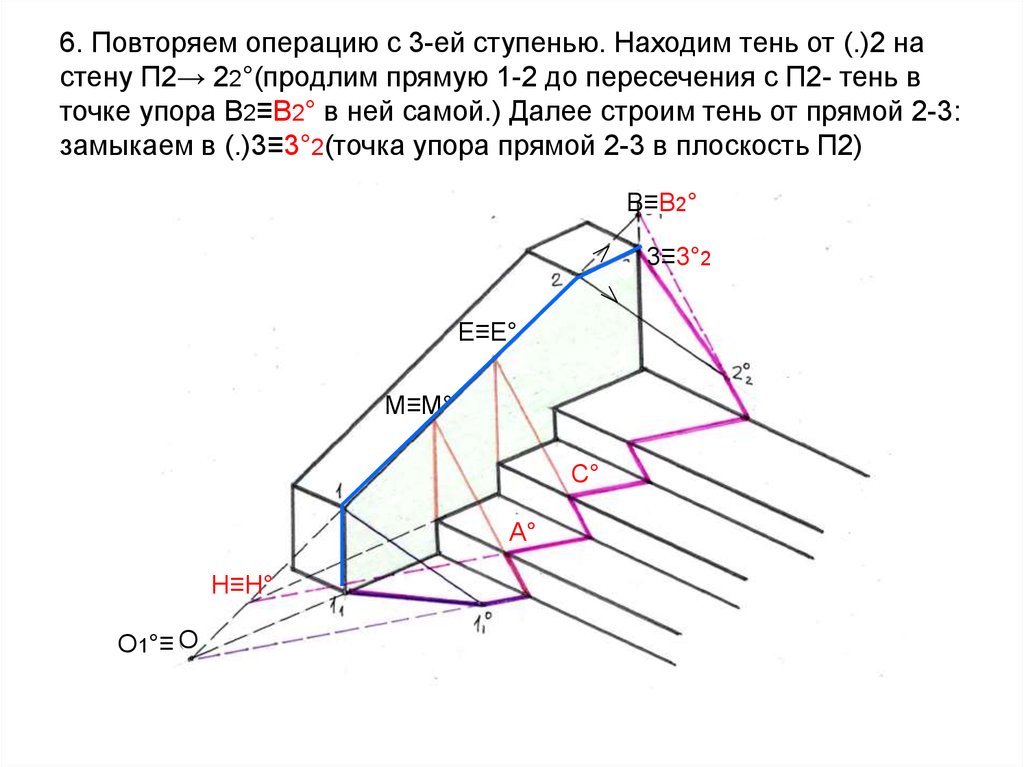
57. 6. Повторяем операцию с 3-ей ступенью. Находим тень от (.)2 на стену П2→ 22°(продлим прямую 1-2 до пересечения с П2- тень в
точке упора В2≡В2° в ней самой.) Далее строим тень от прямой 2-3:замыкаем в (.)3≡3°2(точка упора прямой 2-3 в плоскость П2)
В≡В2°
3≡3°2
Е≡Е°
М≡М°
С°
А°
Н≡Н°
О1°≡ О
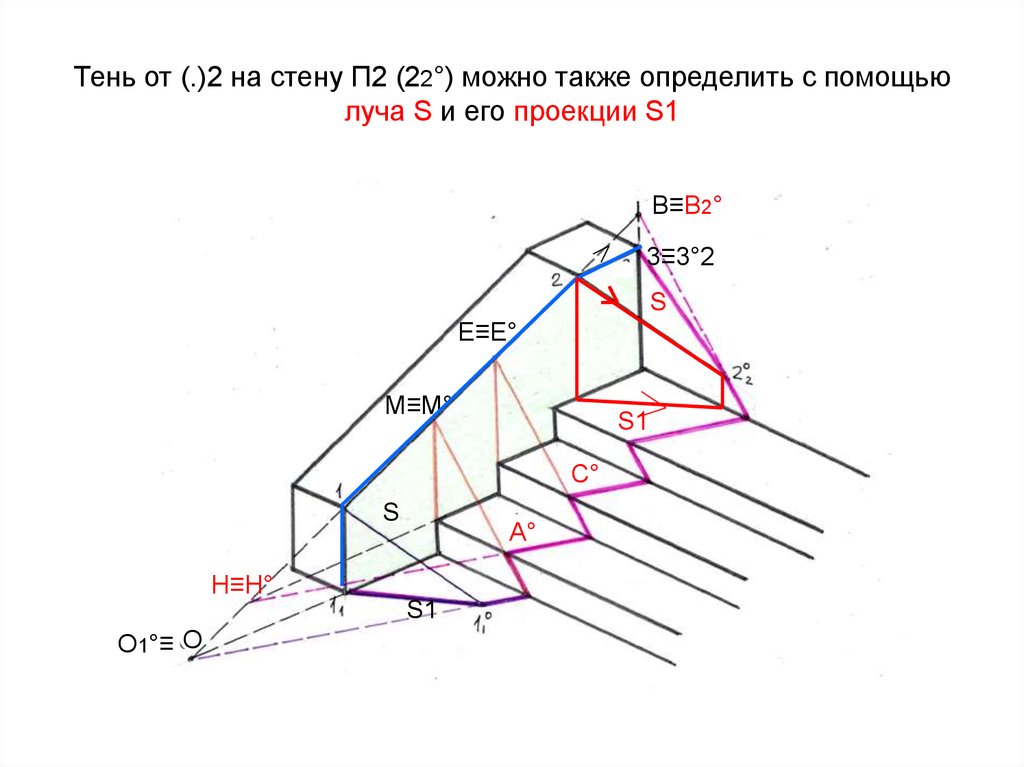
58. Тень от (.)2 на стену П2 (22°) можно также определить с помощью луча S и его проекции S1
В≡В2°
2
3≡3°2
S
Е≡Е°
М≡М°
S1
С°
S
А°
Н≡Н°
S1
О1°≡ О
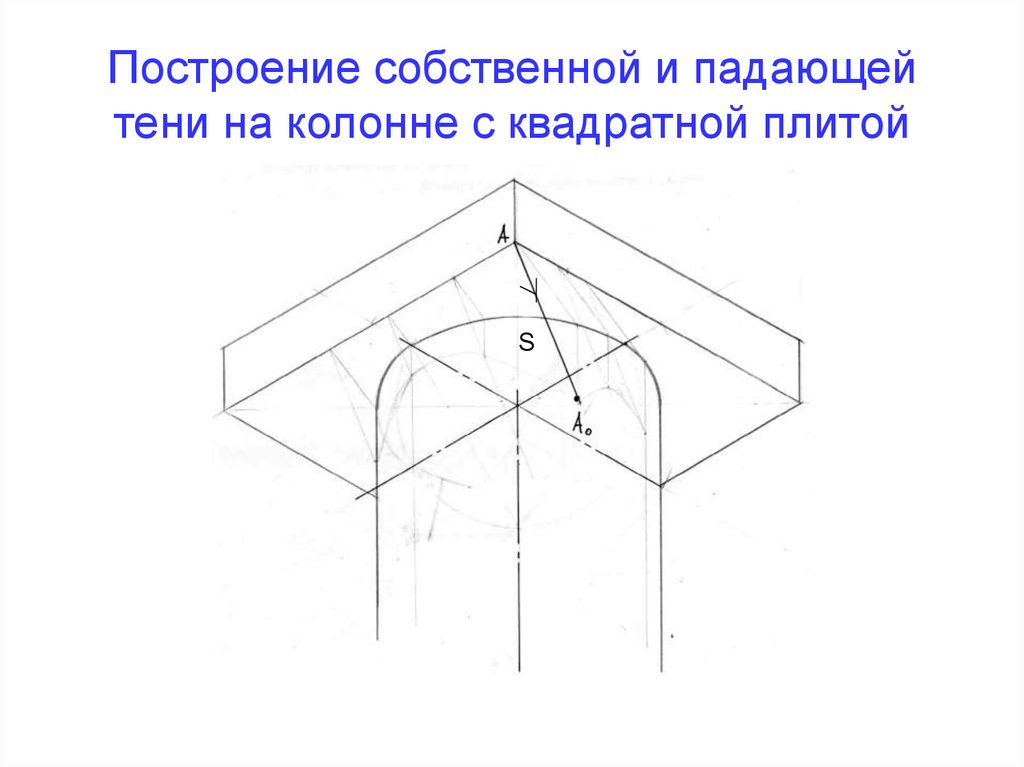
59. Построение собственной и падающей тени на колонне с квадратной плитой
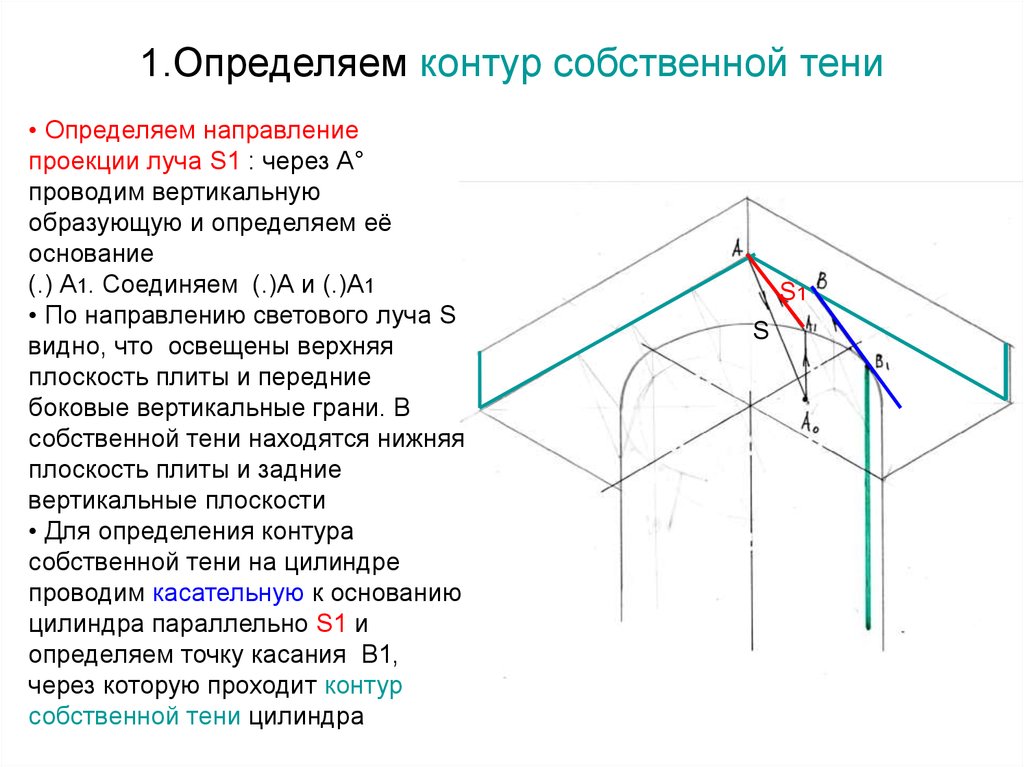
S60. 1.Определяем контур собственной тени
• Определяем направлениепроекции луча S1 : через А°
проводим вертикальную
образующую и определяем её
основание
(.) А1. Соединяем (.)А и (.)А1
• По направлению светового луча S
видно, что освещены верхняя
плоскость плиты и передние
боковые вертикальные грани. В
собственной тени находятся нижняя
плоскость плиты и задние
вертикальные плоскости
• Для определения контура
собственной тени на цилиндре
проводим касательную к основанию
цилиндра параллельно S1 и
определяем точку касания В1,
через которую проходит контур
собственной тени цилиндра
S1
S
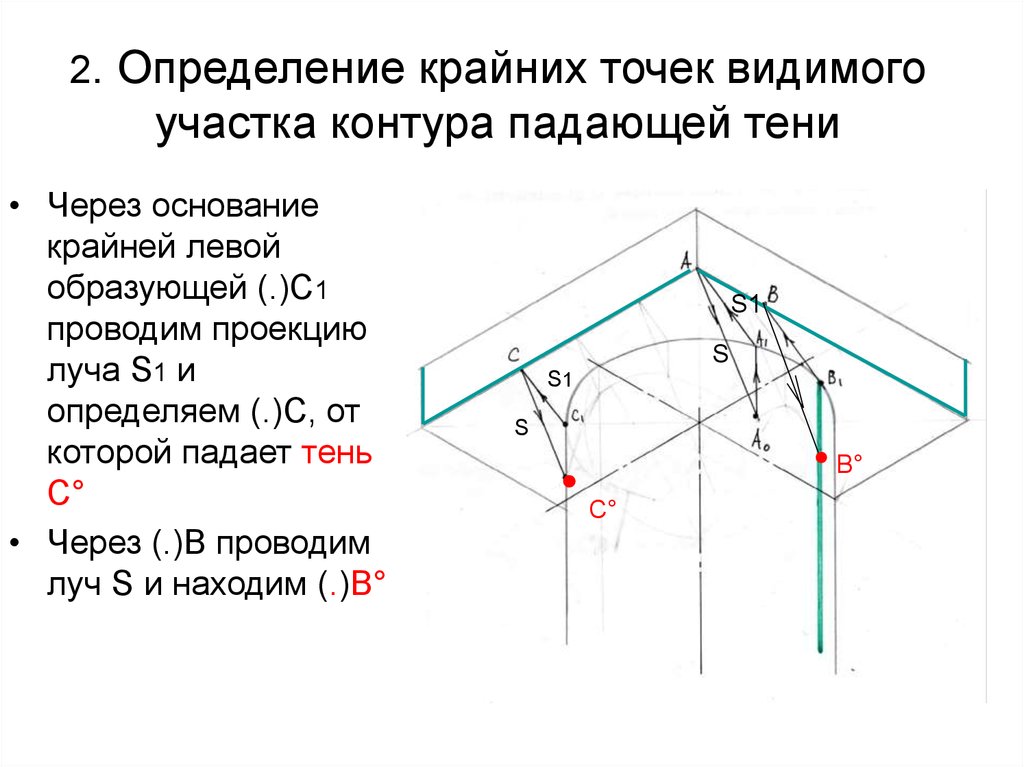
61. 2. Определение крайних точек видимого участка контура падающей тени
• Через основаниекрайней левой
образующей (.)С1
проводим проекцию
луча S1 и
определяем (.)С, от
которой падает тень
С°
• Через (.)В проводим
луч S и находим (.)В°
S1
S
S1
S
● В°
С°
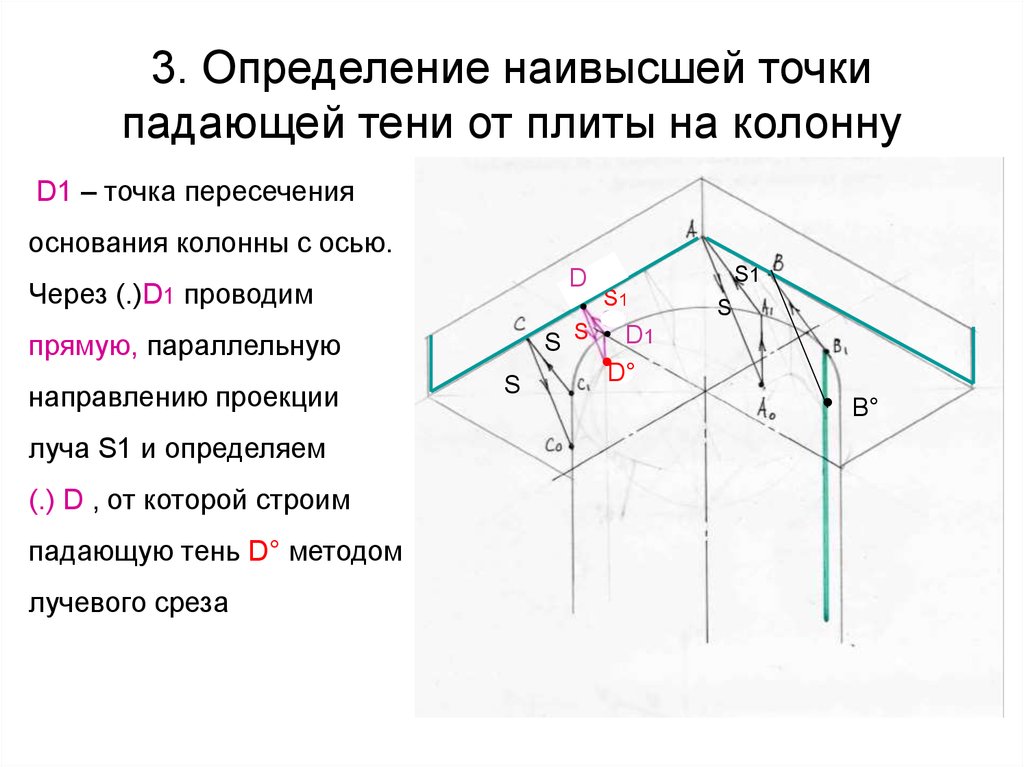
62. 3. Определение наивысшей точки падающей тени от плиты на колонну
D1 – точка пересеченияоснования колонны с осью.
D
Через (.)D1 проводим
S S
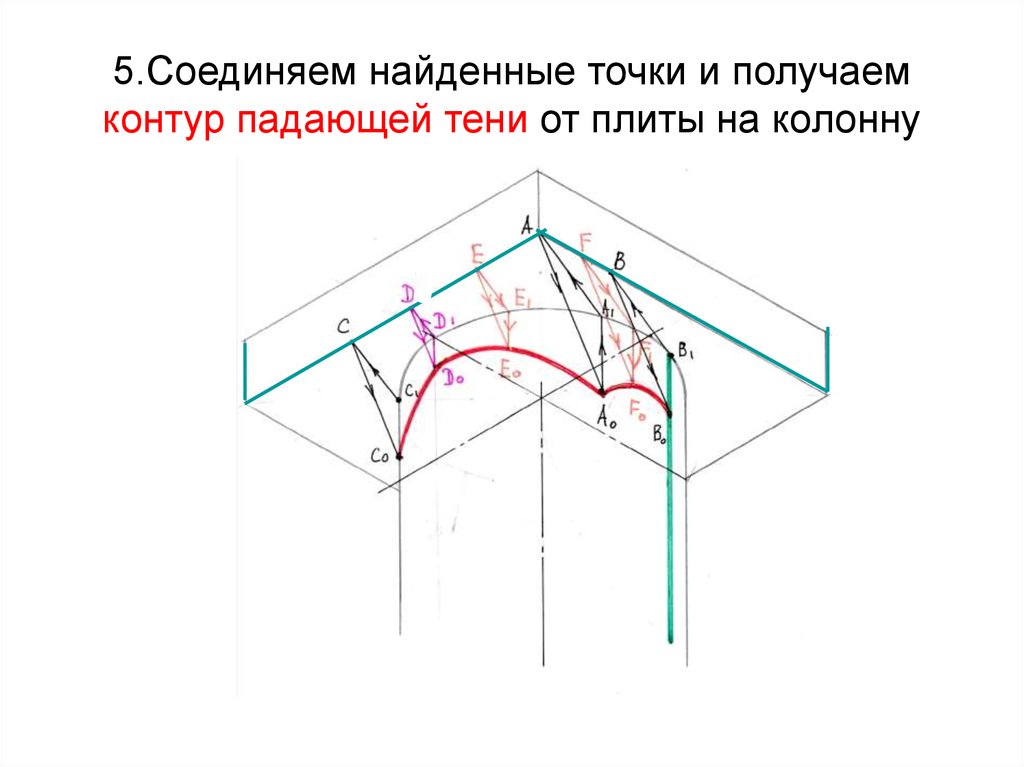
прямую, параллельную
направлению проекции
луча S1 и определяем
(.) D , от которой строим
падающую тень D° методом
лучевого среза
S
S1
S1
S
D1
D°
В°
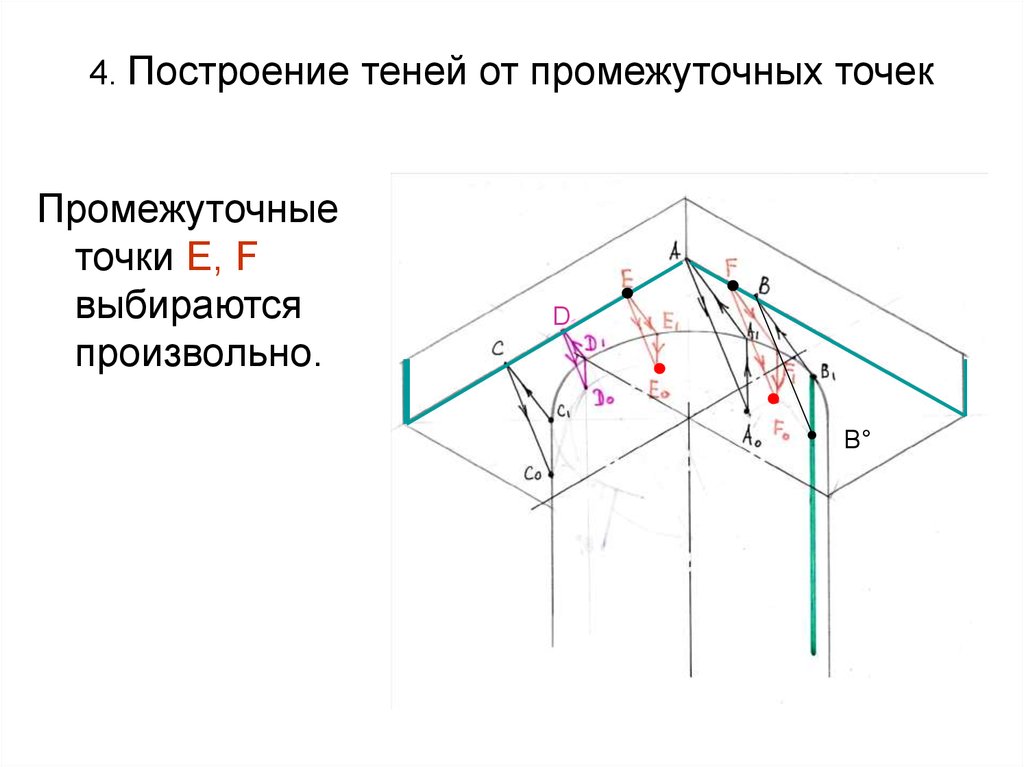
63. 4. Построение теней от промежуточных точек
Промежуточныеточки Е, F
выбираются
произвольно.
D
В°
64. 5.Соединяем найденные точки и получаем контур падающей тени от плиты на колонну
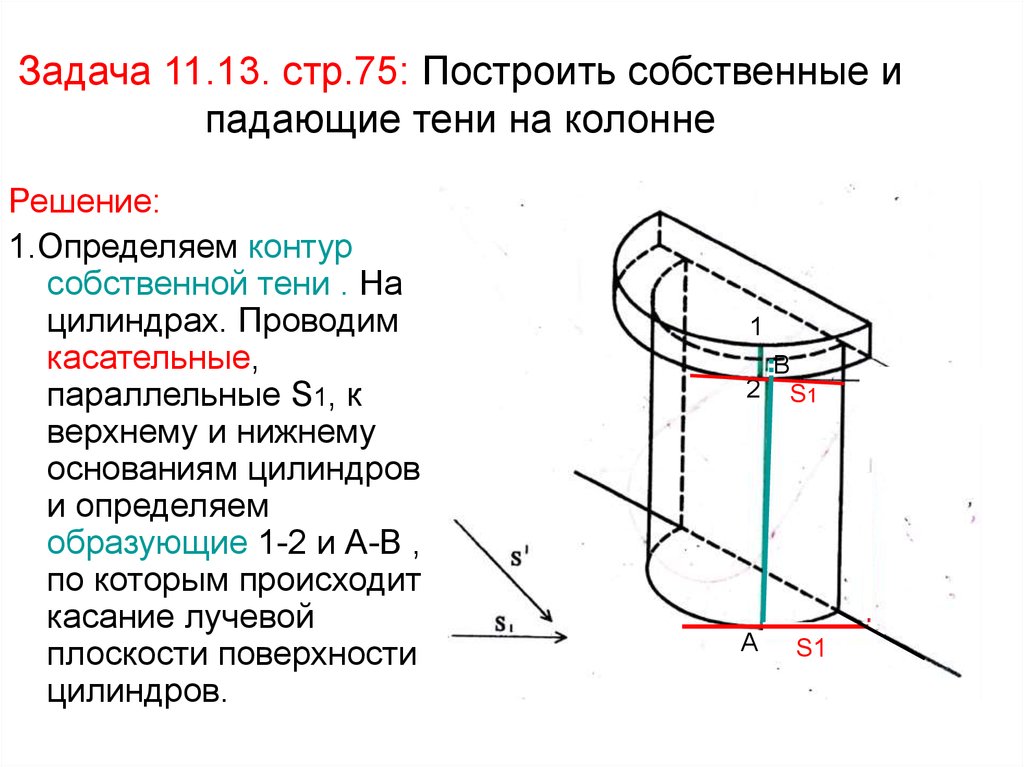
65. Задача 11.13. стр.75: Построить собственные и падающие тени на колонне
Решение:1.Определяем контур
собственной тени . На
цилиндрах. Проводим
касательные,
параллельные S1, к
верхнему и нижнему
основаниям цилиндров
и определяем
образующие 1-2 и А-В ,
по которым происходит
касание лучевой
плоскости поверхности
цилиндров.
1
В
2 S1
А
S1
66.
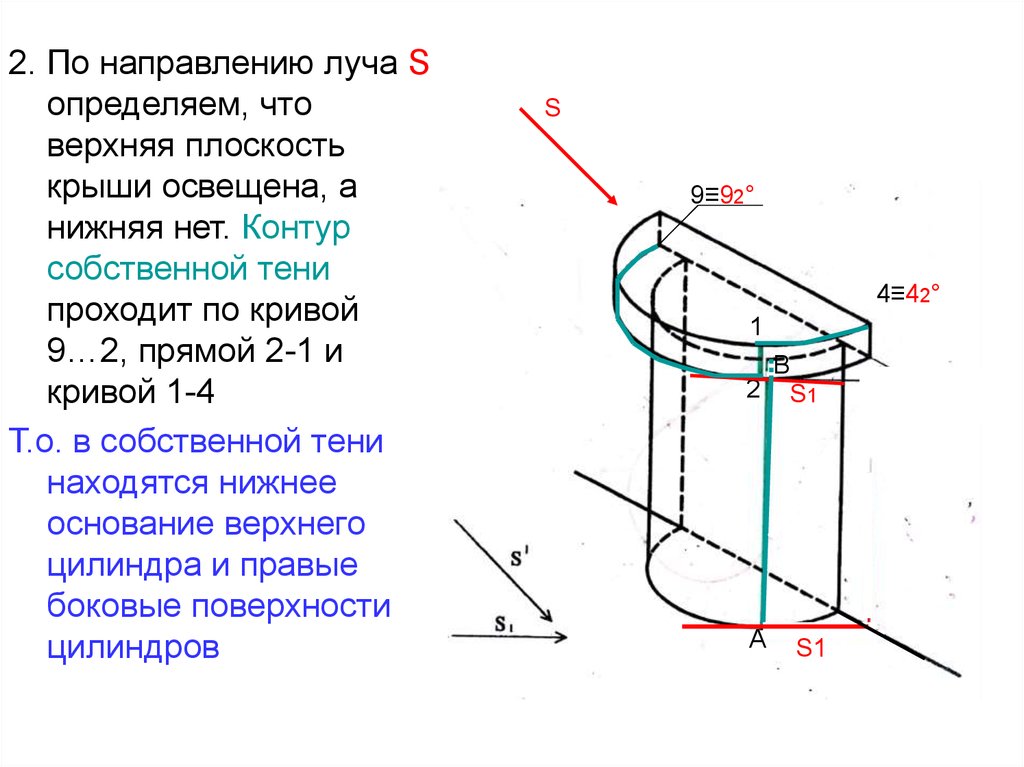
2. По направлению луча Sопределяем, что
верхняя плоскость
крыши освещена, а
нижняя нет. Контур
собственной тени
проходит по кривой
9…2, прямой 2-1 и
кривой 1-4
Т.о. в собственной тени
находятся нижнее
основание верхнего
цилиндра и правые
боковые поверхности
цилиндров
S
9≡92°
4≡42°
1
В
2 S1
А
S1
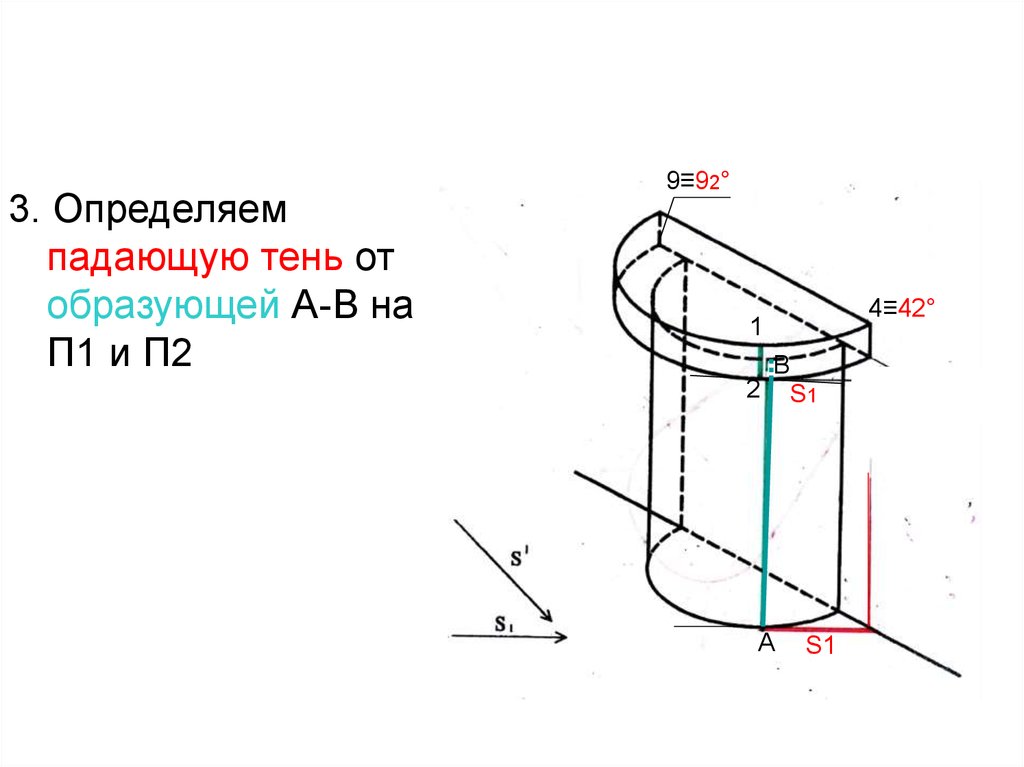
67.
3. Определяемпадающую тень от
образующей А-В на
П1 и П2
9≡92°
4≡42°
1
В
2 S1
А
S1
68. 4. Строим падающую тень от образующей 1-2 на стену:
т.к. (.)2 принадлежит нижнейплоскости верхнего
цилиндра, она совпадает со
своей проекцией на эту
плоскость. Проводим через
(.) 2 луч S и проекцию луча
S1. Определяем
пересечение луча S с П2 →
получим тень 2°2
9≡92°
4≡42°
1
В
2 S1
S
● 2°2
S1
А
S1
69.
Т.к. прямая 1-2параллельна П2, тень
от нее равна и
параллельна этой
прямой
9≡92°
12°-22°‖1-2;
12°-22°=1-2
4≡42°
1
2
В
S
S1
● 1°2
● 2°2
S1
А
S1
70.
5. Строим тень откривой 1-4.
Произвольно на
контуре
собственной тени
1-4 выбираем
промежуточную
точку 3 и строим
тень 32° ,
используя линию
врезки верхней
плоскости крыши в
П2
9≡92°
3 S1
4≡42°
В
S
S
А
● 32°
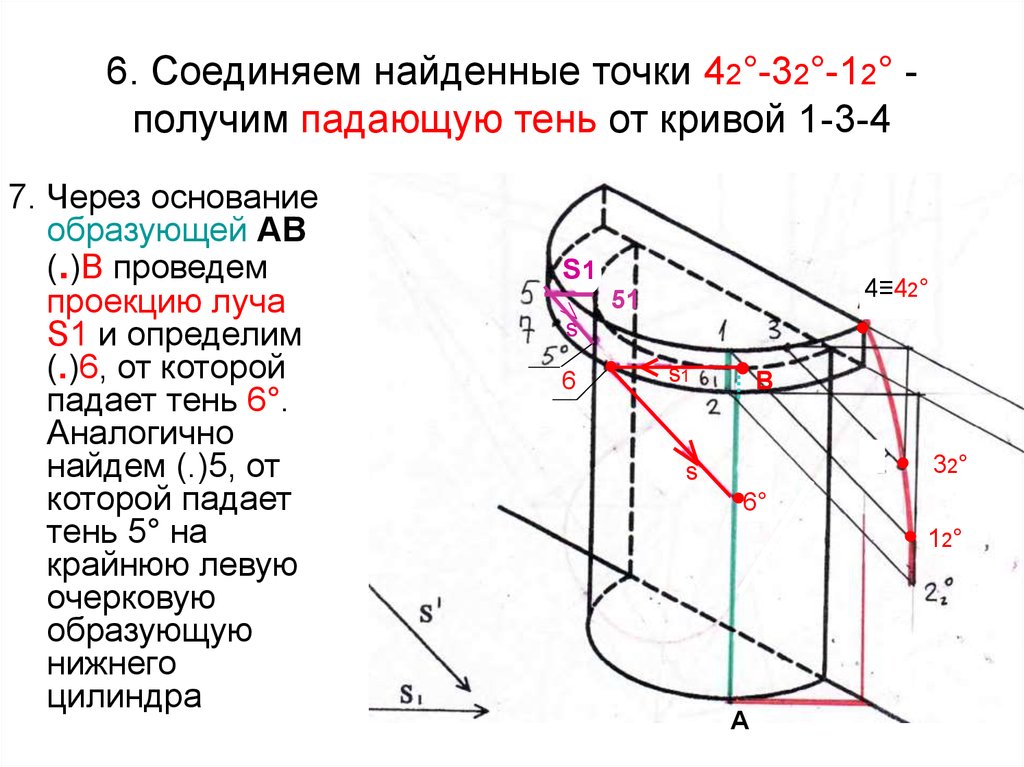
71. 6. Соединяем найденные точки 42°-32°-12° -получим падающую тень от кривой 1-3-4
6. Соединяем найденные точки 42°-32°-12° получим падающую тень от кривой 1-3-47. Через основание
образующей АВ
(.)В проведем
проекцию луча
S1 и определим
(.)6, от которой
падает тень 6°.
Аналогично
найдем (.)5, от
которой падает
тень 5° на
крайнюю левую
очерковую
образующую
нижнего
цилиндра
S1
4≡42°
51
s
6
s1
s
●В
● 32°
●6°
● 12°
А
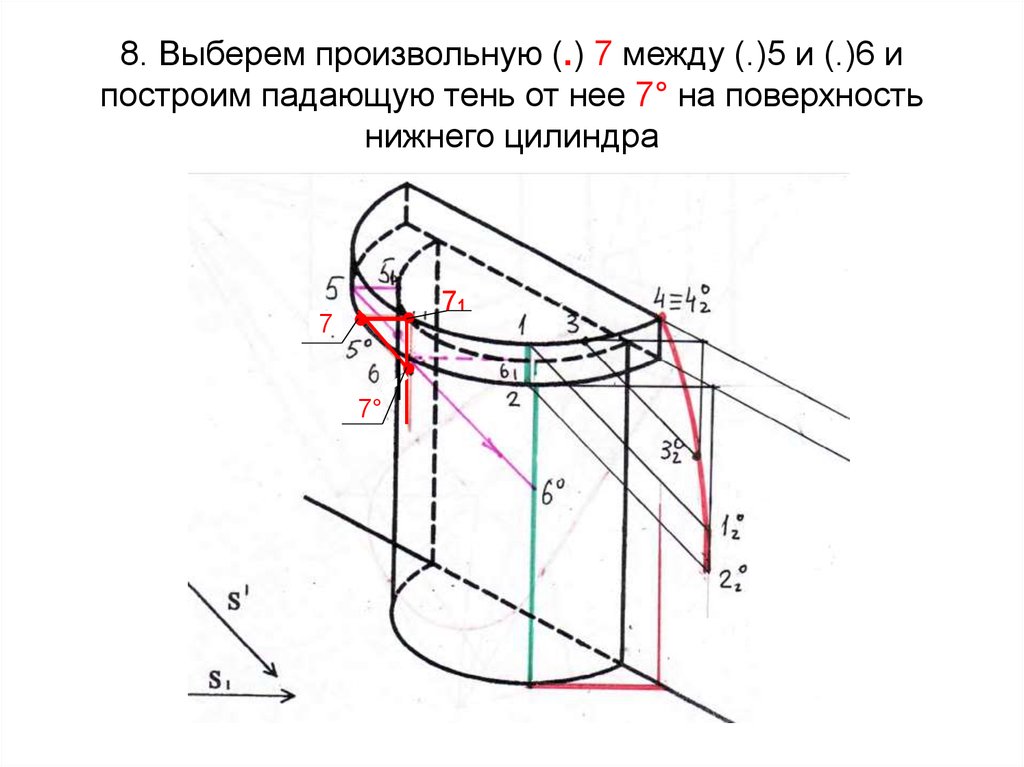
72. 8. Выберем произвольную (.) 7 между (.)5 и (.)6 и построим падающую тень от нее 7° на поверхность нижнего цилиндра
77°
71
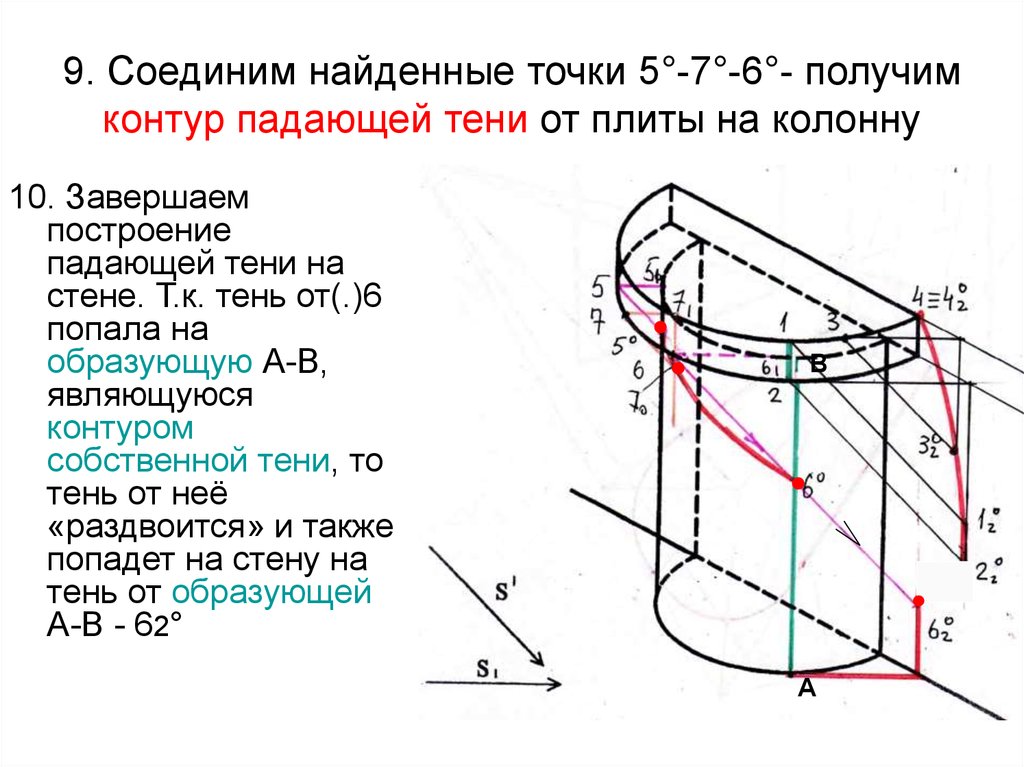
73. 9. Соединим найденные точки 5°-7°-6°- получим контур падающей тени от плиты на колонну
10. Завершаемпостроение
падающей тени на
стене. Т.к. тень от(.)6
попала на
образующую А-В,
являющуюся
контуром
собственной тени, то
тень от неё
«раздвоится» и также
попадет на стену на
тень от образующей
А-В - 62°
В
А
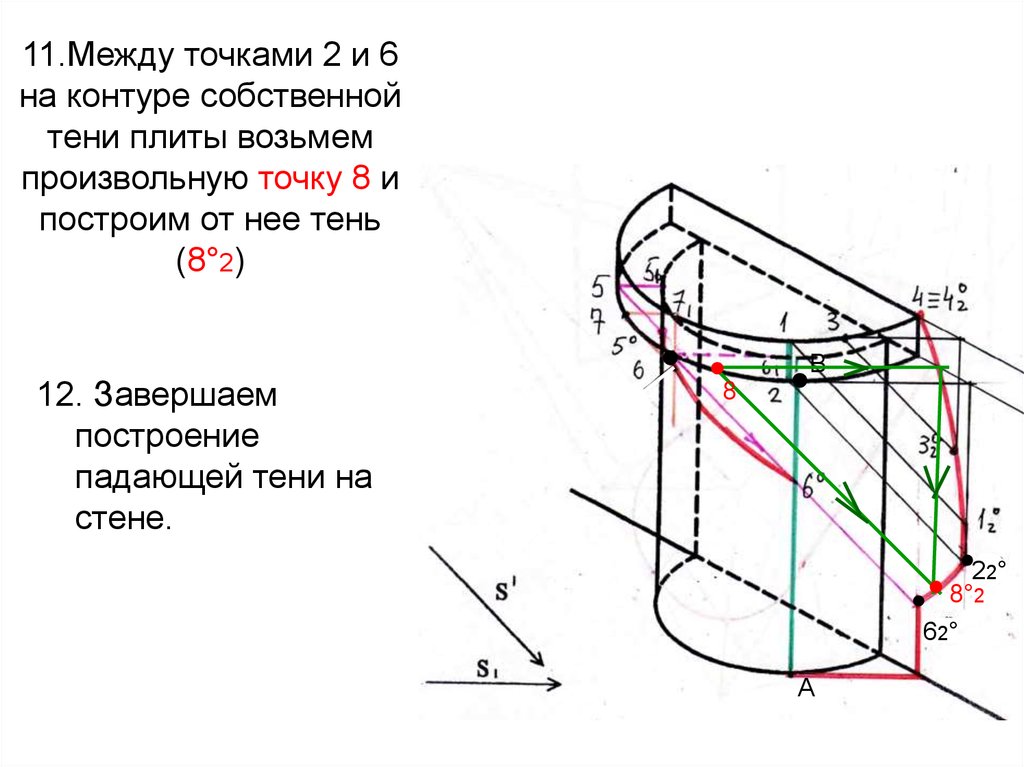
74. 11.Между точками 2 и 6 на контуре собственной тени плиты возьмем произвольную точку 8 и построим от нее тень (8°2)
12. Завершаемпостроение
падающей тени на
стене.
●
8
В
●22°
● 8°2
62°
А








 drafting
drafting








