Геодезия. Задачи геодезии в разных циклах строительного производства

1. ГЕОДЕЗИЯ

Кафедра
Геоэкология и инженерная геология
2015 – 16 уч. год
Доц. А.Т.Глухов

2. ЛИТЕРАТУРА

Инженерная геодезия: учебник для студ. высш. учеб. заведений /
Е.Б. Клюшин, М.И. Киселев, Д.Ш. Михелев, В.Д. Фельдман; под ред.
Д.Ш. Михелева. – 8-е изд., стер. – М.: Изд. Центр “Академия”, 2008.
– 480 с.
Федотов Г.А. Инженерная геодезия: учебник / Г.А. Федотов. – 4-е
изд. стер. – М.: Высш. шк., 2007. – 463 с.
Сборник задач и упражнений по геоинформатике: учеб. пособие /
Е.Г. Капралов, и др.; под ред. В.С. Тикунова. – 2-е изд. Перераб и
доп. – М.: Академия, 2009. – 512 с.
Интернет- ресурс
Михелев Д.Ш. Инженерная геодезия: учебник /Е.Б. Клюшин [и
др.]; под ред. Д.Ш.Михелева, - 9-е изд. стер. – Электронные
текстовые данные –М.: ИЦ «Академия», 2008.

3. ВВЕДЕНИЕ Задачи геодезии в разных циклах строительного производства

В период проектирования:
сбор исходной картографической информации для принципиального
решения вопроса размещения объекта строительства;
съемочные работы в крупном масштабе для детального проектирования
элементов объекта строительства.
В период строительства:
определение местоположения площадки строительства и пространственное
размещение в плане и по высоте элементов запроектированного
сооружения;
геодезическое сопровождение строительства объекта для контроля
правильности возведения конструкции в целом и взаимного расположения
его элементов.
В период эксплуатации:
исполнительная съемка для контроля правильности завершенного
строительства и выявления отступлений от проекта;
геодезические работы по определению эксплуатационных сдвигов объекта в
целом и смещений его элементов для контроля и прогноза устойчивости
конструкции.

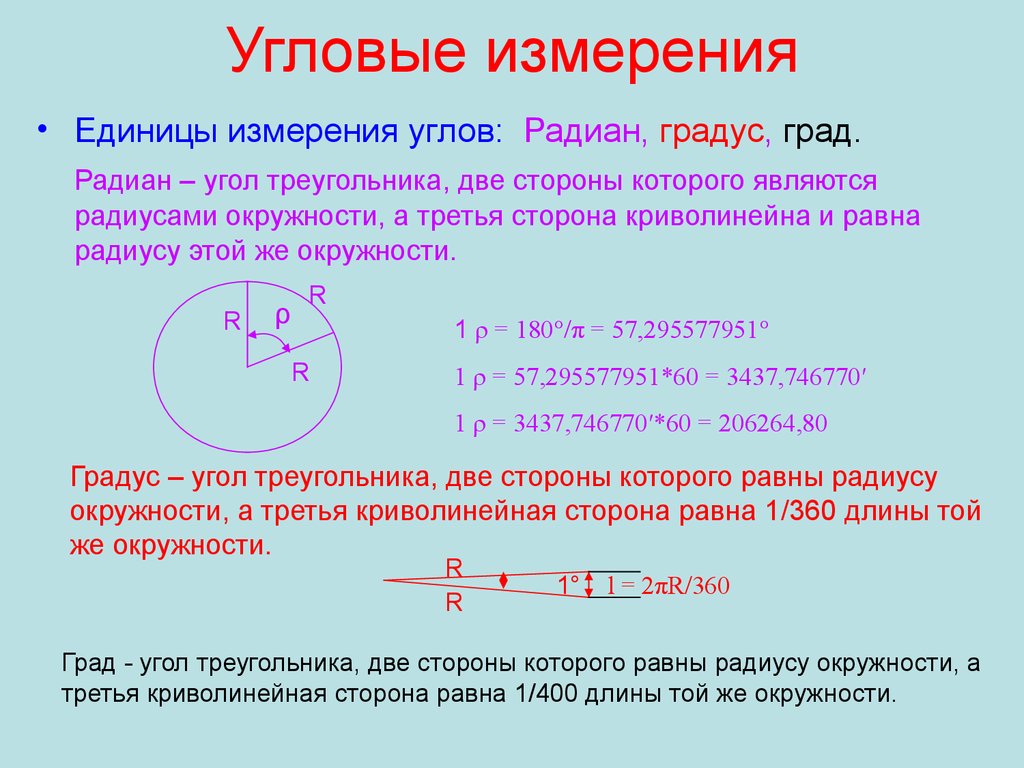
4. Угловые измерения

• Единицы измерения углов: Радиан, градус, град.
Радиан – угол треугольника, две стороны которого являются
радиусами окружности, а третья сторона криволинейна и равна
радиусу этой же окружности.
R
ρ
R
1 ρ = 180°/π = 57,295577951°
R
1 ρ = 57,295577951*60 = 3437,746770′
1 ρ = 3437,746770′*60 = 206264,80
Градус – угол треугольника, две стороны которого равны радиусу
окружности, а третья криволинейная сторона равна 1/360 длины той
же окружности.
R
R
1°
l = 2πR/360
Град - угол треугольника, две стороны которого равны радиусу окружности, а
третья криволинейная сторона равна 1/400 длины той же окружности.

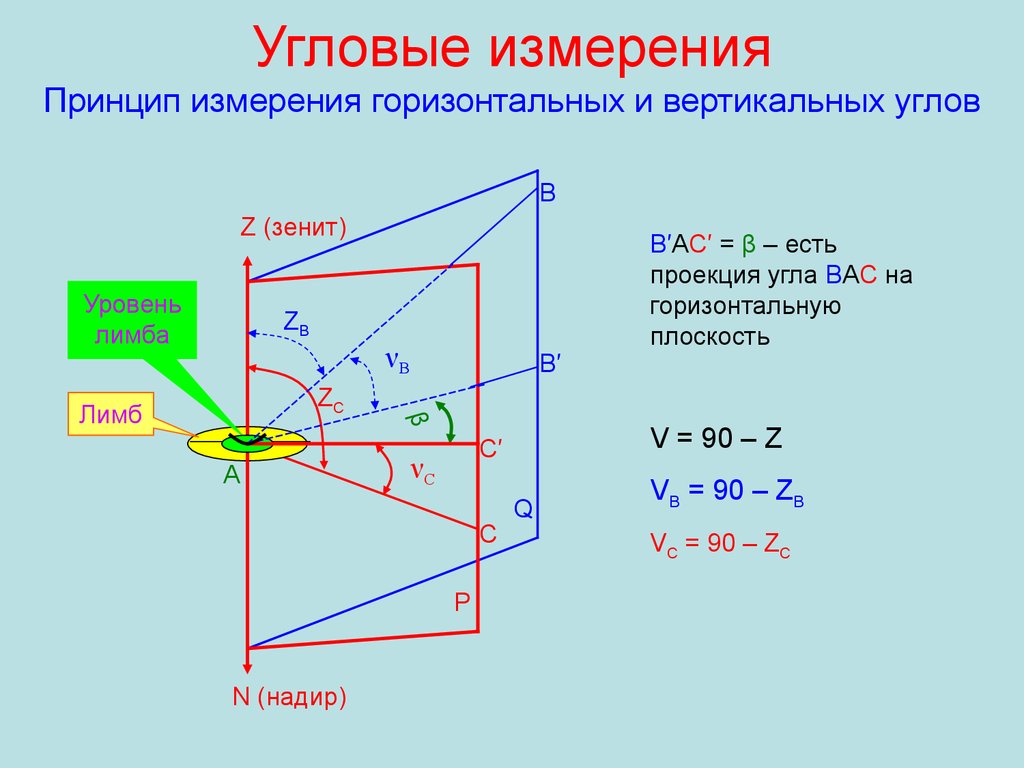
5. Угловые измерения Принцип измерения горизонтальных и вертикальных углов

В
Z (зенит)
Уровень
лимба
ZB
νB
А
β
ZC
Лимб
В′
С
P
N (надир)
V = 90 – Z
С′
νC
B′AC′ = β – есть
проекция угла ВАС на
горизонтальную
плоскость
Q
VB = 90 – ZB
VC = 90 – ZC

6. Угловые измерения Прибор для измерения горизонтальных и вертикальных углов

Вертикальный круг
Отсчетное
устройство
(объектив, окуляр)
Визирная оптическая труба
Горизонтальный круг
(лимб, алидада)
Подставка
Основные части
теодолита 2Т30

7. Угловые измерения Конструкция теодолита (тахеометра): Принцип устройства

2С
Ось вращения оптической
зрительной трубы
90
°
Вертикальный круг
Коллимационная
погрешность
Оптический центр
(фокус) объектива
оптической трубы
90°
Сетка нитей
Уровень при
горизонтальном круге
Лимб горизонтального круга
90°
Визирная ось оптической
зрительной трубы
Ось уровня при
горизонтальном круге
Ось вращения теодолита

8. Угловые измерения Поверки теодолита (тахеометра)

90°
1. Ось уровня при горизонтальном круге
должна быть перпендикулярна оси
вращения теодолита.
2. Визирная ось оптической зрительной
трубы должна быть перпендикулярна оси
вращения трубы.
90
°
90°
3. Ось вращения оптической зрительной
трубы должна быть перпендикулярна оси
вращения теодолита
Н
δ
α
01 03 2012 г
a 1
H

9. Угловые измерения Поверки теодолита (тахеометра)

Ось вращения
трубы
4. Вертикальная нить сетки нитей
должна быть перпендикулярна а
горизонтальная нить должна быть
параллельна оси вращения трубы
теодолита.
5. Рен. Расстояние между соседними
градусными делениями лимба (а)
должно быть равно расстоянию
между нулевым и шестым штрихом
алидады (b).
90°
Сетка нитей
0
ai = b
159
b
6
а
А
158
V0
4. Место нуля вертикального круга
должно быть равно нулю.
V = V0 ±МО
МО = (КП – КЛ)/2
Горизонтальная
линия
V
+МО
V0
-М0

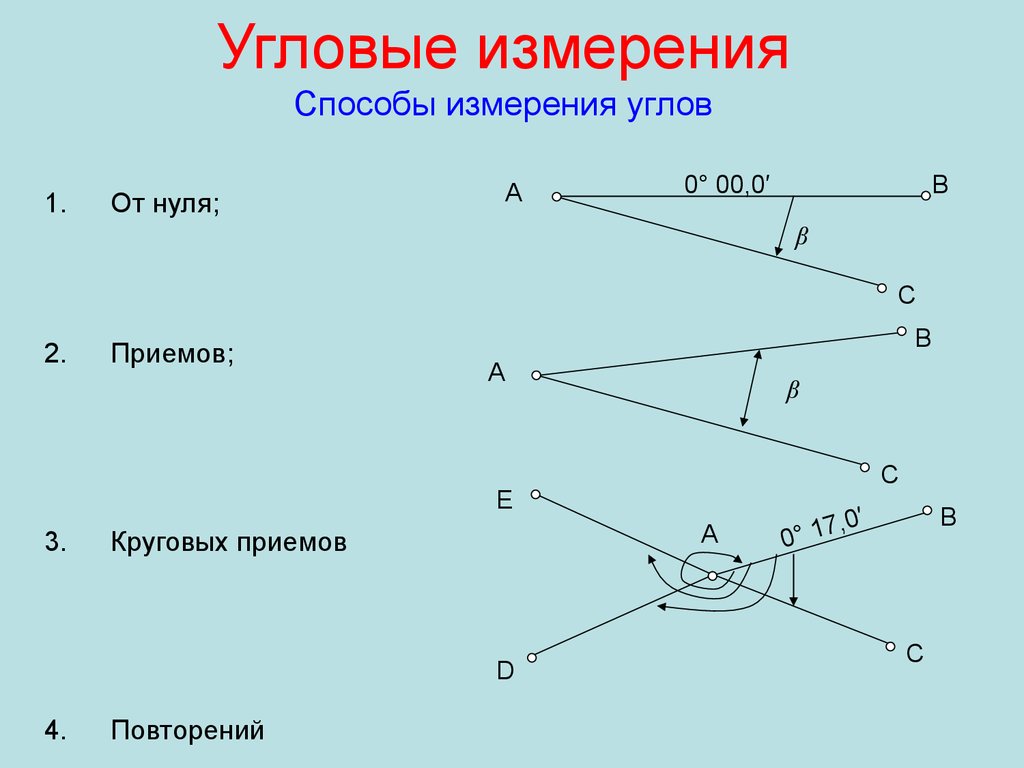
10. Угловые измерения Способы измерения углов

1.
А
От нуля;
0° 00,0′
В
β
С
2.
Приемов;
В
А
β
С
E
3.
А
Круговых приемов
D
4.
Повторений
7,0′
1
°
0
В
С

11. Угловые измерения Точность измерения углов

Погрешность центрирования
A1
Погрешность
центрирования
Погрешность редукции
A β
A1
ΔβA = βA1 – βA
B
βA
βB
βB1
ΔβB = βB1 – βB
B1
ΔβC = βC1 – βC
ΔβD = βD1 – βD
βC
βD
D
C
Погрешность
редукции
ΣΔβ = fβ = (βA1 – βA) + (βB1 - βB ) +
+(βC1 - βC)+ (βD1- βD)
fβ = Σβизм – Σβтеор
fβ = Σβизм – 180 (n – 2)

12. Угловые измерения Точность измерения углов

Δβ1, Δβ2, …, Δβn
f(x)
или
x1, x2, …, xn
t=1
t = 1,96
-m
x
1
f ( x)
e
m 2
m
-2m
2m
-3m
x x 2
i ср2
2m
3m
t=3
f (доп) t m n
m
( xi xср )
i
n 1
2

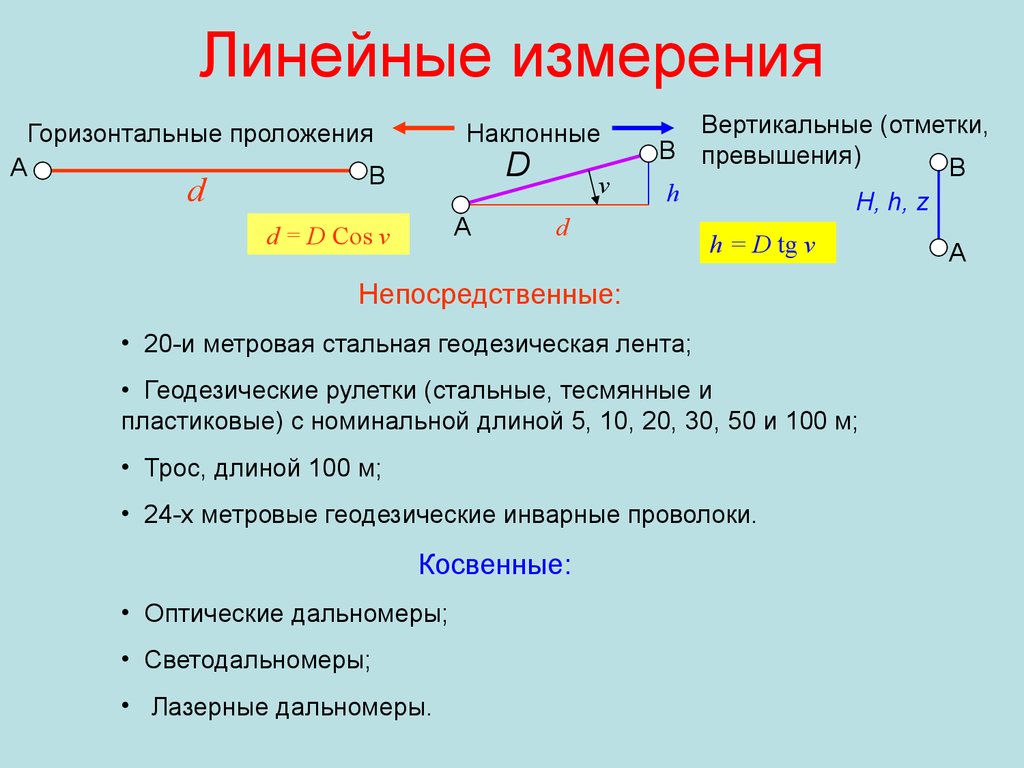
13. Линейные измерения

Горизонтальные проложения
A
d
Наклонные
D
B
А
d = D Cos v
v
В
h
d
Вертикальные (отметки,
превышения)
В
H, h, z
h = D tg v
Непосредственные:
• 20-и метровая стальная геодезическая лента;
• Геодезические рулетки (стальные, тесмянные и
пластиковые) с номинальной длиной 5, 10, 20, 30, 50 и 100 м;
• Трос, длиной 100 м;
• 24-х метровые геодезические инварные проволоки.
Косвенные:
• Оптические дальномеры;
• Светодальномеры;
• Лазерные дальномеры.
А

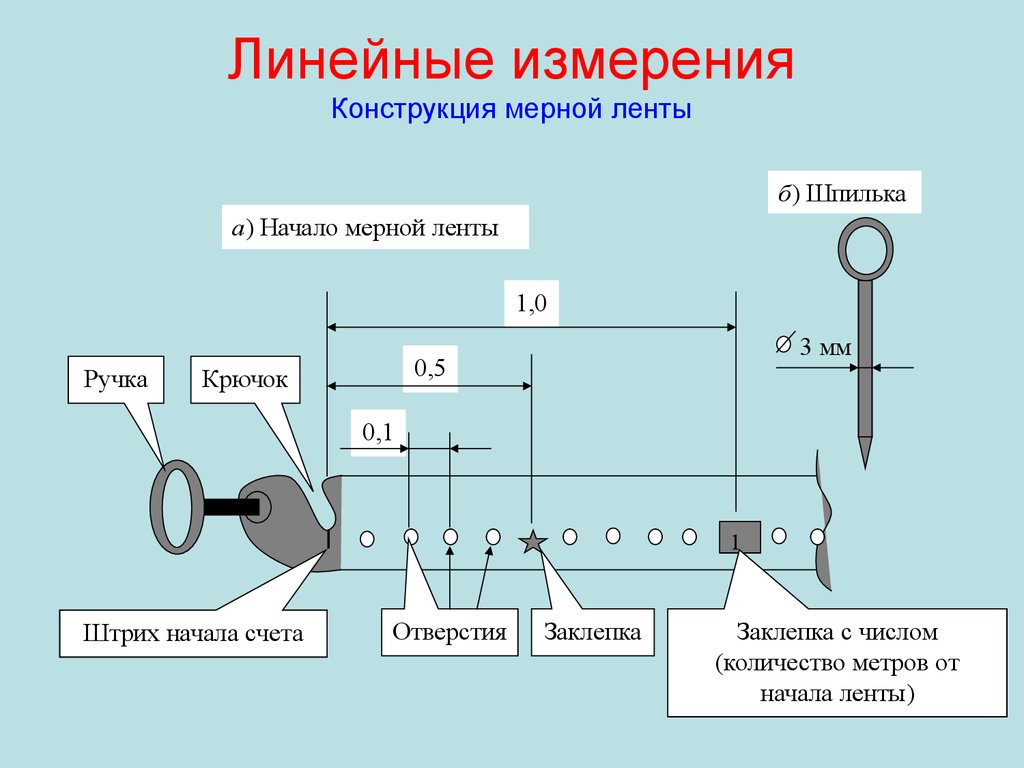
14. Линейные измерения Конструкция мерной ленты

б) Шпилька
а) Начало мерной ленты
1,0
Ручка
3 мм
0,5
Крючок
0,1
1
Штрих начала счета
Отверстия
Заклепка
Заклепка с числом
(количество метров от
начала ленты)

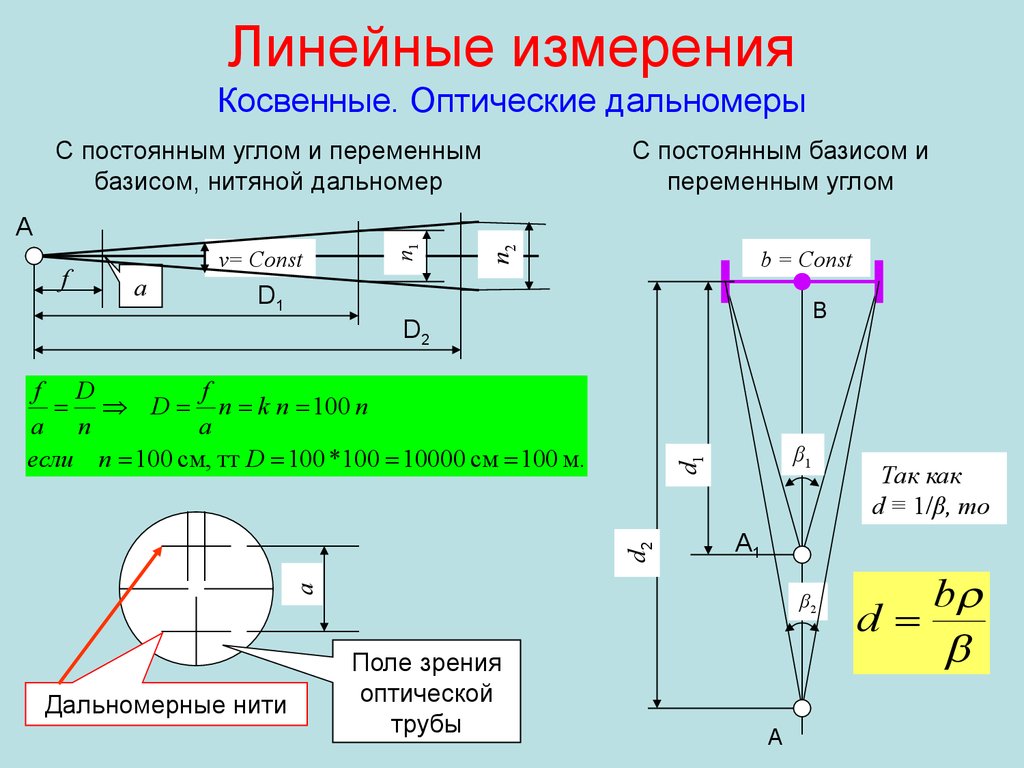
15. Линейные измерения Косвенные. Оптические дальномеры

С постоянным углом и переменным
базисом, нитяной дальномер
С постоянным базисом и
переменным углом
а
n2
f
v= Const
n1
A
b = Const
D1
B
D2
β1
Дальномерные нити
β2
Поле зрения
оптической
трубы
Так как
d ≡ 1/β, то
A1
а
d2
d1
f D
f
D n k n 100 n
a n
a
если n 100 см, тт D 100 *100 10000 см 100 м.
A
b
d

16. Линейные измерения Косвенные. Светодальномер. Лазерный дальномер

D = Vt/2
h′AB
v
l
h′AB = D Sin v
i
hAB = h′AB + i - l
d = D Cos v
А
15 03 2012
В

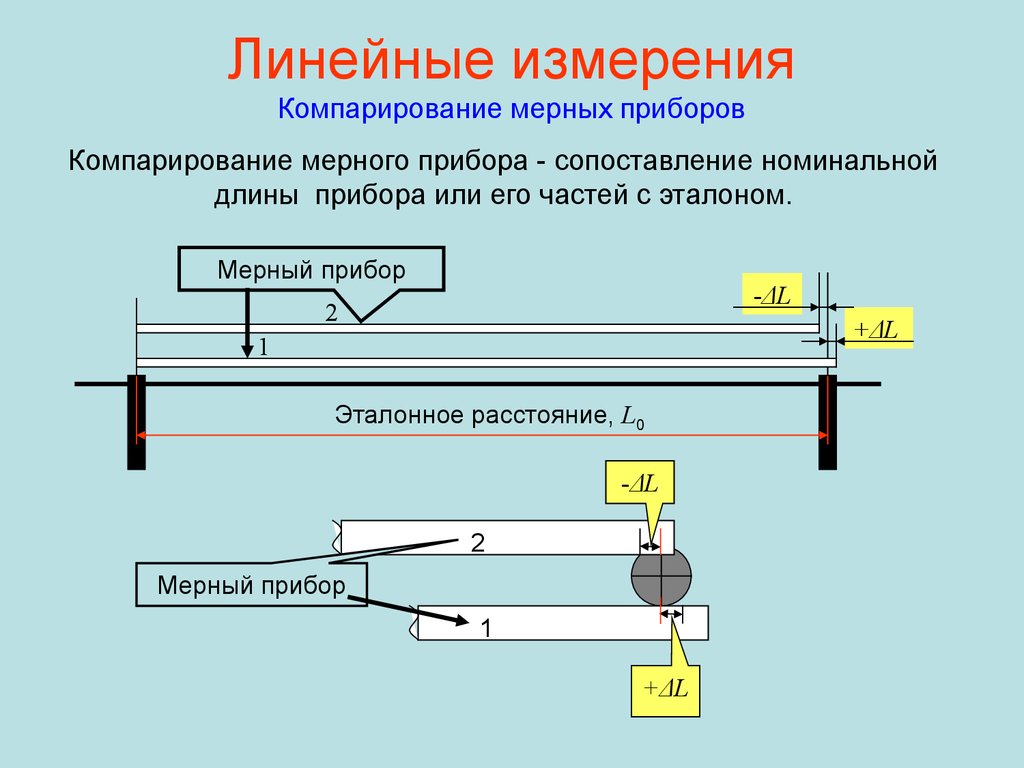
17. Линейные измерения Компарирование мерных приборов

Компарирование мерного прибора - сопоставление номинальной
длины прибора или его частей с эталоном.
Мерный прибор
-ΔL
2
+ΔL
1
Эталонное расстояние, L0
-ΔL
2
Мерный прибор
1
+ΔL

18. Линейные измерения

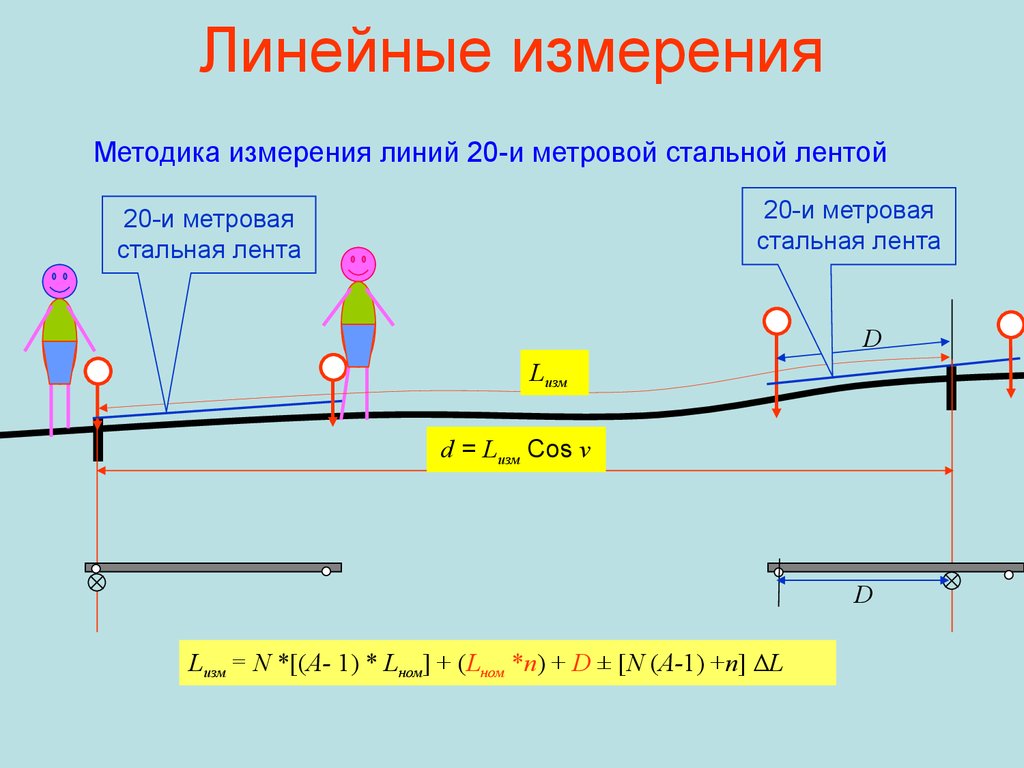
Методика измерения линий 20-и метровой стальной лентой
20-и метровая
стальная лента
20-и метровая
стальная лента
D
Lизм
d = Lизм Cos v
D
Lизм = N *[(А- 1) * Lном] + (Lном *n) + D ± [N (A-1) +n] ΔL

19. Линейные измерения Геометрическое нивелирование из середины

h2 = з2 – п2
h1 = з1 – п1
2
1
з1
A
п2
з2
п1
h1
B
h2
hAB
X1
hAB = h1 + h2
HA
HB = HA + hAB
Уровень Балтийского моря
HB

20. Линейные измерения Геометрическое нивелирование способом вперед

hАВ = ЗА – ПВ
ГИ = НА + ЗА
HB = HA + hAB
Hпр = ГИ - Пр
ПВ
ПрС
ЗА
А
ПрD
ПрE
С
HA
HС
HD
В
F
E
D
ПрF
HВ
ГИ
HE
Уровень Балтийского моря
HF

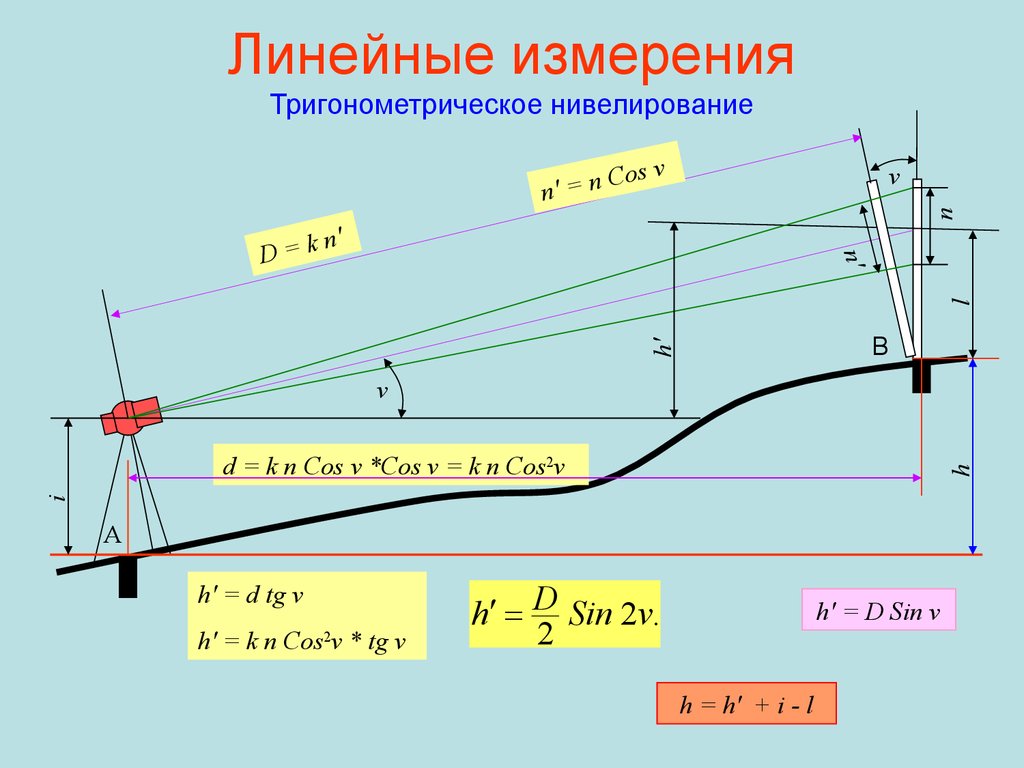
21. Линейные измерения Тригонометрическое нивелирование

os v
v
n
C
n′ = n
n′
l
n′
D=k
h′
В
v
i
h
d = k n Cos v *Cos v = k n Cos2v
А
h′ = d tg v
h′ = k n Cos2v * tg v
h D Sin 2v.
2
h′ = D Sin v
h = h′ + i - l

22. ФИГУРА ЗЕМЛИ И МЕТОД ПРОЕКЦИЙ

Общая фигура Земли, как планеты. Географическая, геодезическая и
астрономическая системы координат.
Равноугольная поперечно-цилиндрическая проекция Земной
поверхности (проекция Гаусса-Крюгера).
Плоская прямоугольная зональная система координат.
Ориентирование линий на Земной поверхности. Истинный и
магнитный азимут, дирекционный угол, румб.
Склонение магнитной стрелки. Сближение меридианов. Связь между
истинным и магнитным азимутами, истинным азимутом и
дирекционным углом.

23. ОБЩАЯ ФИГУРА ЗЕМЛИ, КАК ПЛАНЕТЫ

ЭВОЛЮЦИЯ ПРЕДСТАВЛЕНИЯ ЛЮДЕЙ
О ФОРМЕ ЗЕМЛИ
первое –
второе –
третье –
четвертое –
Плоскость;
Шар;
Эллипсоид вращения;
Геоид

24. ПЛАН И КАРТА

• План – уменьшенное изображение земной
поверхности выполненное в ортогональной
проекции:
без искажения расстояний и углов;
имеет место подобие геометрических фигур;
первое представление людей о форме Земли.
• Карта - уменьшенное изображение земной
поверхности выполненное в специальной
картографической проекции:
искажаются либо расстояния либо углы;
отсутствует подобие геометрических фигур;
второе или третье представление людей о форме Земли.

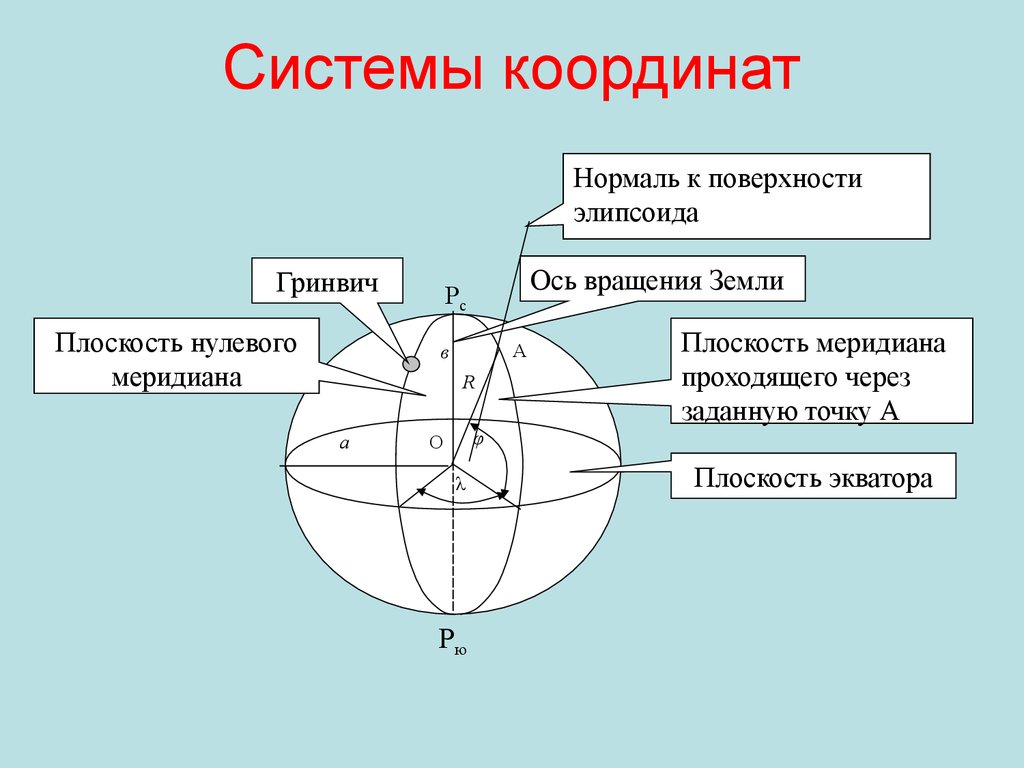
25. Системы координат

Нормаль к поверхности
элипсоида
Гринвич
Плоскость нулевого
меридиана
Ось вращения Земли
Рс
А
в
R
а
Плоскость меридиана
проходящего через
заданную точку А
φ
О
λ
Pю
Плоскость экватора

26. РАВНОУГОЛЬНАЯ ПОПЕРЕЧНО-ЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ ЗЕМНОЙ ПОВЕРХНОСТИ (ПРОЕКЦИЯ ГАУССА-КРЮГЕРА)

РАВНОУГОЛЬНАЯ ПОПЕРЕЧНОЦИЛИНДРИЧЕСКАЯ ПРОЕКЦИЯ
ЗЕМНОЙ ПОВЕРХНОСТИ
(ПРОЕКЦИЯ ГАУССА-КРЮГЕРА)

27. Проекция Гаусса-Крюгера

Гринвич
X
С
Зона 31
Зона 33
Зона 32
φ = 6°
Y
X = 0 км
Y = 0 км
Ю
X′ = 0 км
Y = 500 км

28. Плоская прямоугольная зональная система координат

№ Зоны
32
33
31
X′
С
X′
X′
С
34
С
X′
X
X′
С
αАВ
yB
0
3
6
9
12
18
15
24
X = 0 км
Y = 0 км
Y
Экватор
Осевой
меридиан зоны
Ю
Ю
Ю
Ю
yB А
xA
В
xB
Y
X′ = 0 км
Y = 500 км

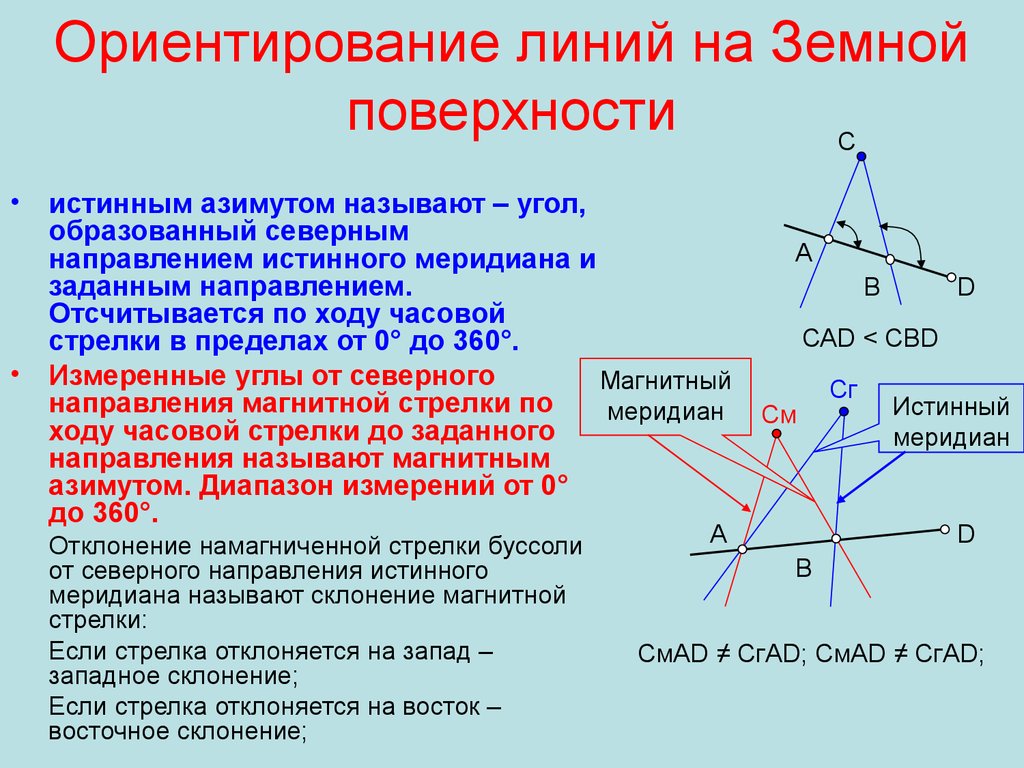
29. Ориентирование линий на Земной поверхности

С
истинным азимутом называют – угол,
образованный северным
направлением истинного меридиана и
заданным направлением.
Отсчитывается по ходу часовой
стрелки в пределах от 0° до 360°.
Измеренные углы от северного
Магнитный
направления магнитной стрелки по
меридиан
ходу часовой стрелки до заданного
направления называют магнитным
азимутом. Диапазон измерений от 0°
до 360°.
Отклонение намагниченной стрелки буссоли
от северного направления истинного
меридиана называют склонение магнитной
стрелки:
Если стрелка отклоняется на запад –
западное склонение;
Если стрелка отклоняется на восток –
восточное склонение;
А
В
D
САD < CВD
См
А
Cг
Истинный
меридиан
D
В
CмАD ≠ CгАD; CмАD ≠ CгАD;

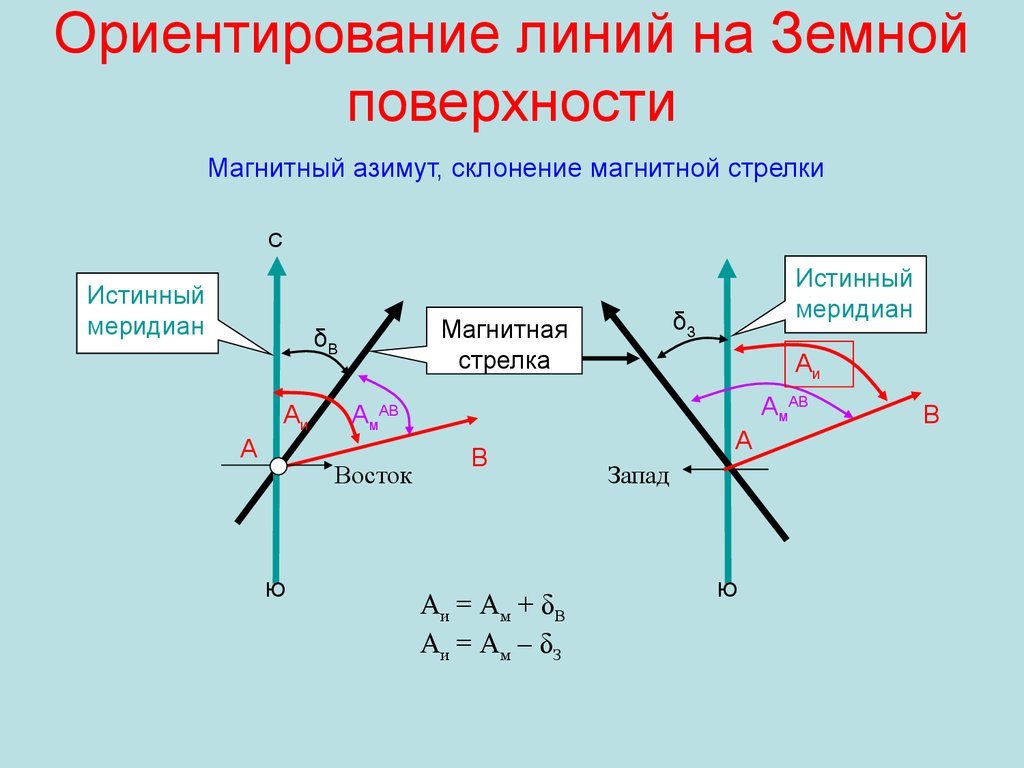
30. Ориентирование линий на Земной поверхности

Магнитный азимут, склонение магнитной стрелки
С
Истинный
меридиан
Аи
А
Аи
АмАВ
АмАВ
Восток
Ю
δЗ
Магнитная
стрелка
δВ
Истинный
меридиан
В
А и = А м + δВ
Аи = А м – δ З
А
Запад
Ю
В

31. Ориентирование линий на Земной поверхности

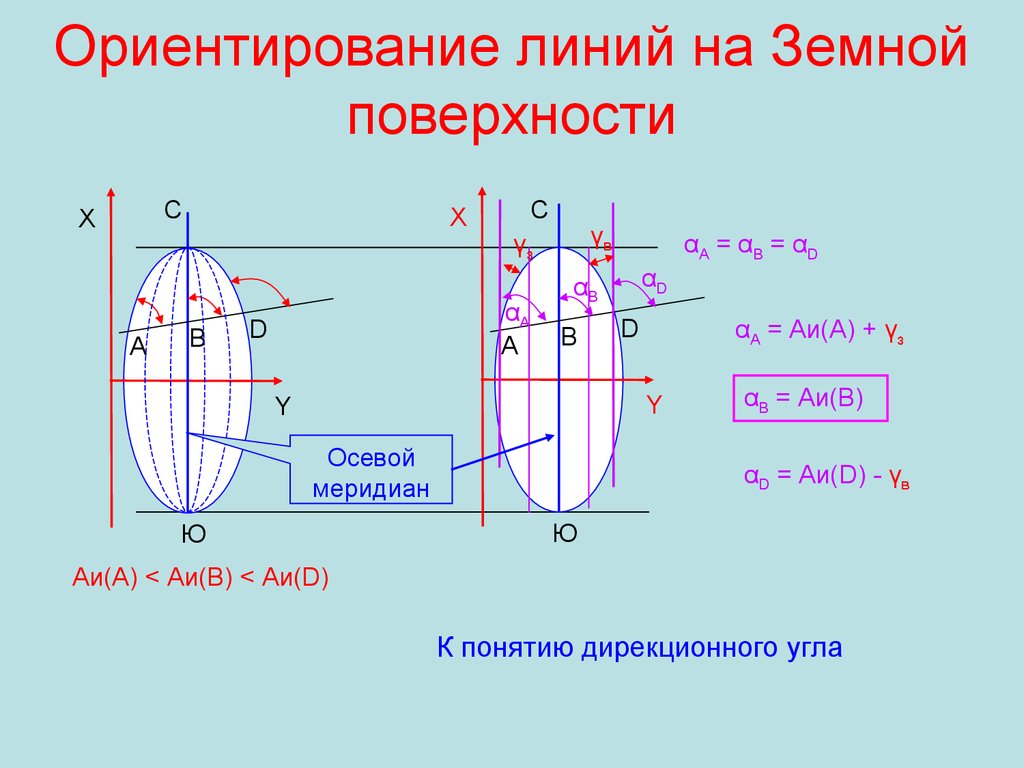
С
X
А
X
В
С
αA
А
D
γв
γз
αА = αВ = αD
αD
αB
В
D
αА = Аи(А) + γз
Y
Y
Осевой
меридиан
Ю
αВ = Аи(В)
αD = Аи(D) - γв
Ю
Аи(А) < Аи(В) < Аи(D)
К понятию дирекционного угла

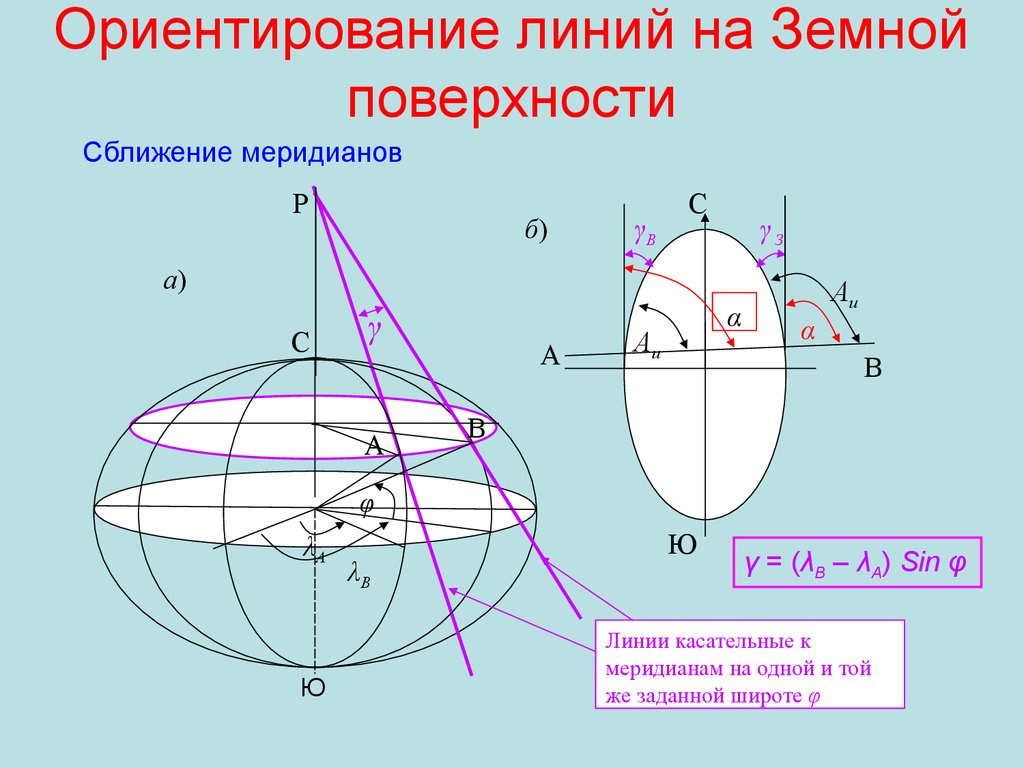
32. Ориентирование линий на Земной поверхности

Сближение меридианов
P
б)
γВ
С
γЗ
а)
С
γ
А
А
α
Аи
Аи
α
В
В
φ
λА
Ю
λВ
Ю
γ = (λВ – λА) Sin φ
Линии касательные к
меридианам на одной и той
же заданной широте φ

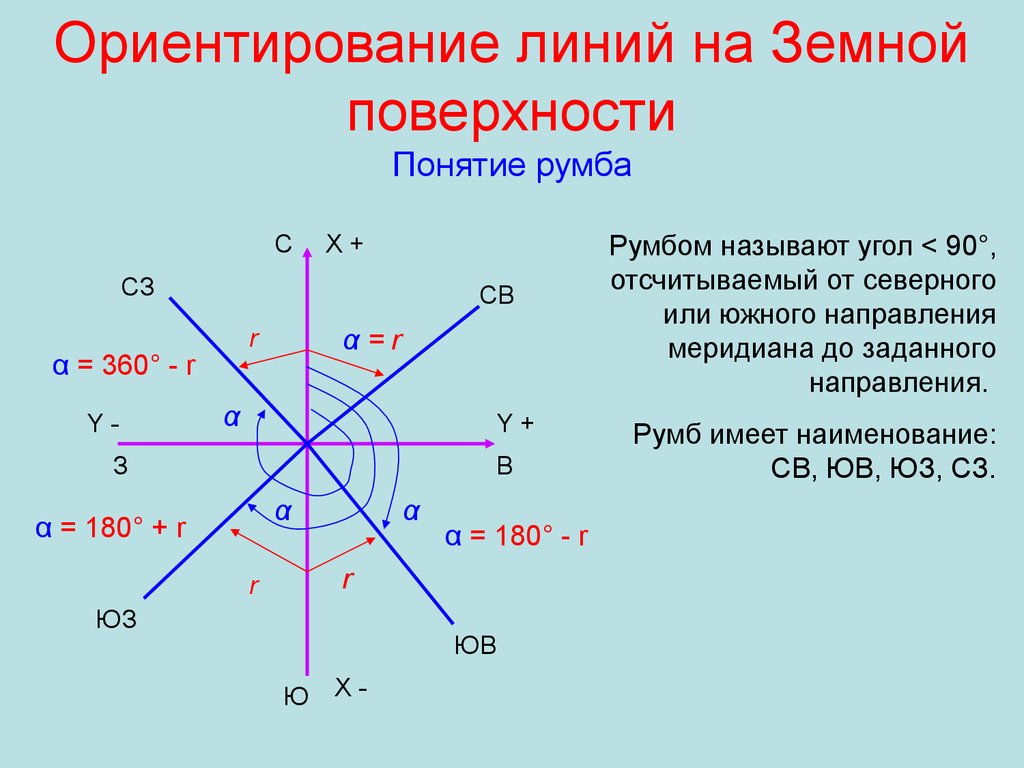
33. Ориентирование линий на Земной поверхности Понятие румба

С
X+
СЗ
СВ
r
α = 360° - r
Y-
α=r
α
Y+
З
В
α
α = 180° + r
r
α
α = 180° - r
r
ЮЗ
ЮВ
Ю X-
Румбом называют угол < 90°,
отсчитываемый от северного
или южного направления
меридиана до заданного
направления.
Румб имеет наименование:
СВ, ЮВ, ЮЗ, СЗ.

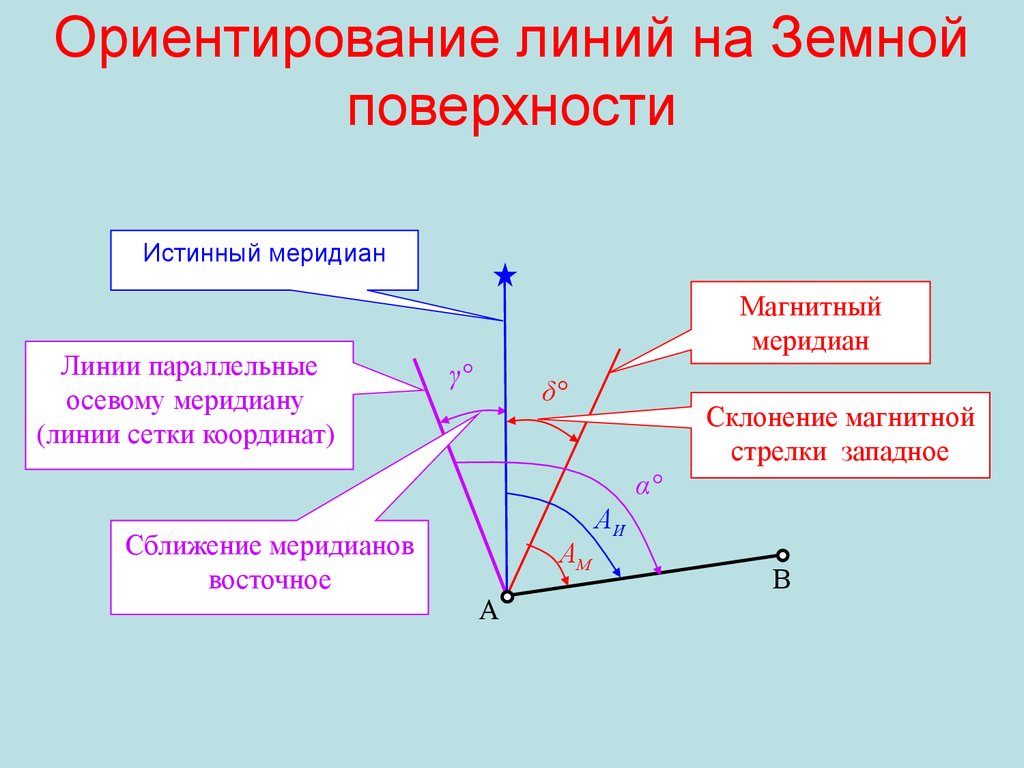
34. Ориентирование линий на Земной поверхности

Истинный меридиан
Линии параллельные
осевому меридиану
(линии сетки координат)
Магнитный
меридиан
γ°
δ°
Склонение магнитной
стрелки западное
α°
Сближение меридианов
восточное
АМ
А
АИ
В

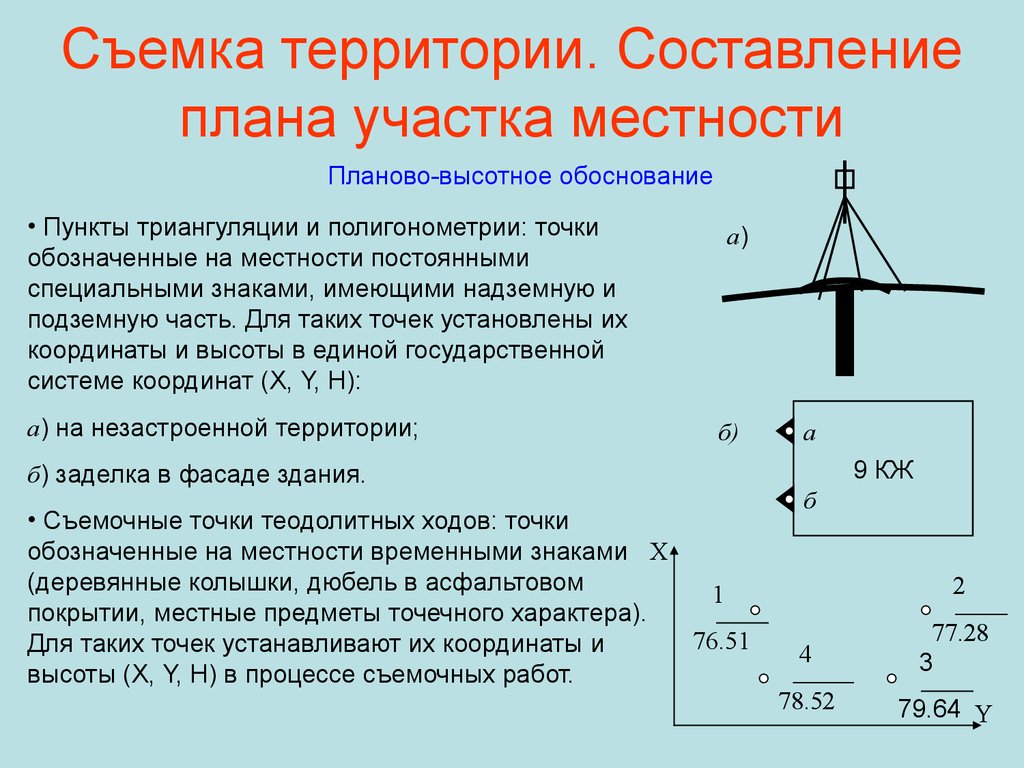
35. Съемка территории. Составление плана участка местности

Планово-высотное обоснование
• Пункты триангуляции и полигонометрии: точки
обозначенные на местности постоянными
специальными знаками, имеющими надземную и
подземную часть. Для таких точек установлены их
координаты и высоты в единой государственной
системе координат (X, Y, H):
а) на незастроенной территории;
а)
б)
б) заделка в фасаде здания.
• Съемочные точки теодолитных ходов: точки
обозначенные на местности временными знаками X
(деревянные колышки, дюбель в асфальтовом
1
покрытии, местные предметы точечного характера).
76.51
Для таких точек устанавливают их координаты и
высоты (X, Y, H) в процессе съемочных работ.
а
9 КЖ
б
2
4
78.52
77.28
3
79.64 Y

36. Съемка территории. Составление плана участка местности

Полевые работы
• Рекогносцировка – осмотр территории съемки;
• Детальная рекогносцировка → закрепление точек временными
знаками (колышки, дюбеля и др.), составление схемы местоположения
точек обоснования;
• Измерение горизонтальных и вертикальных углов между смежными
точками;
• Измерение расстояний между смежными точками;
• Съемка горизонтальной ситуации (теодолитная съемка);
• Геометрическое нивелирование по точкам теодолитного хода;
• Съемка рельефа (нивелирование застроенной территории или
тахеометрическая съемка)

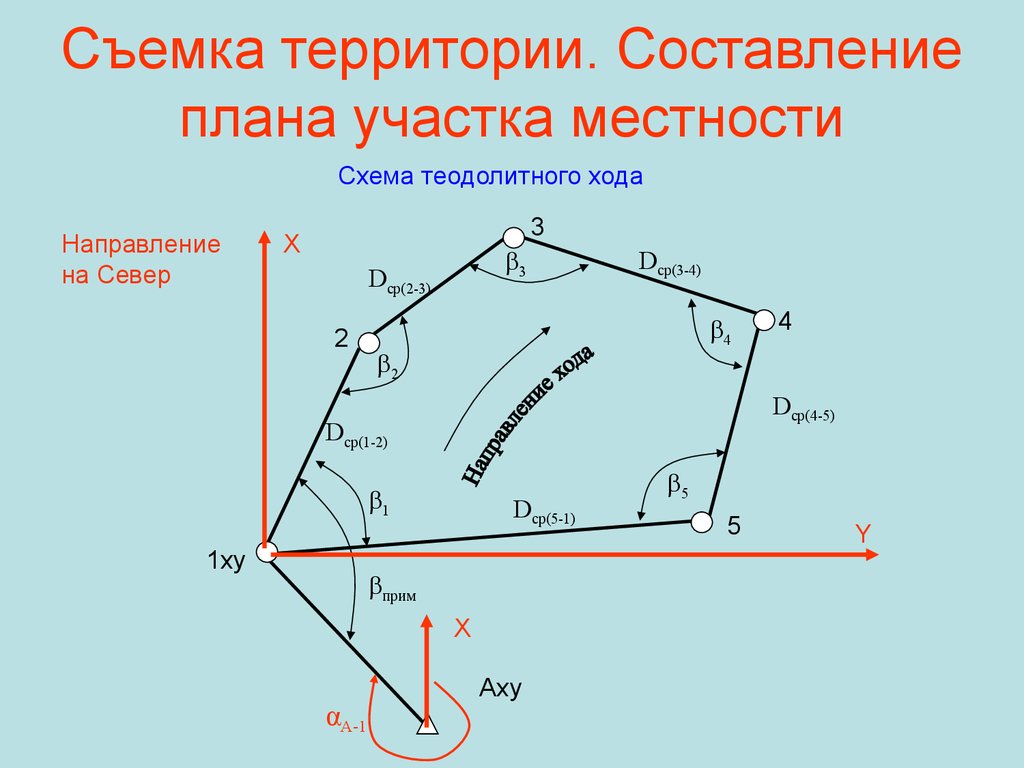
37. Съемка территории. Составление плана участка местности

Схема теодолитного хода
Направление
на Север
3
X
3
Dср(2-3)
2
Dср(3-4)
4
2
Dср(4-5)
Dср(1-2)
1
1xy
Dср(5-1)
прим
X
αA-1
4
Аxy
5
5
Y

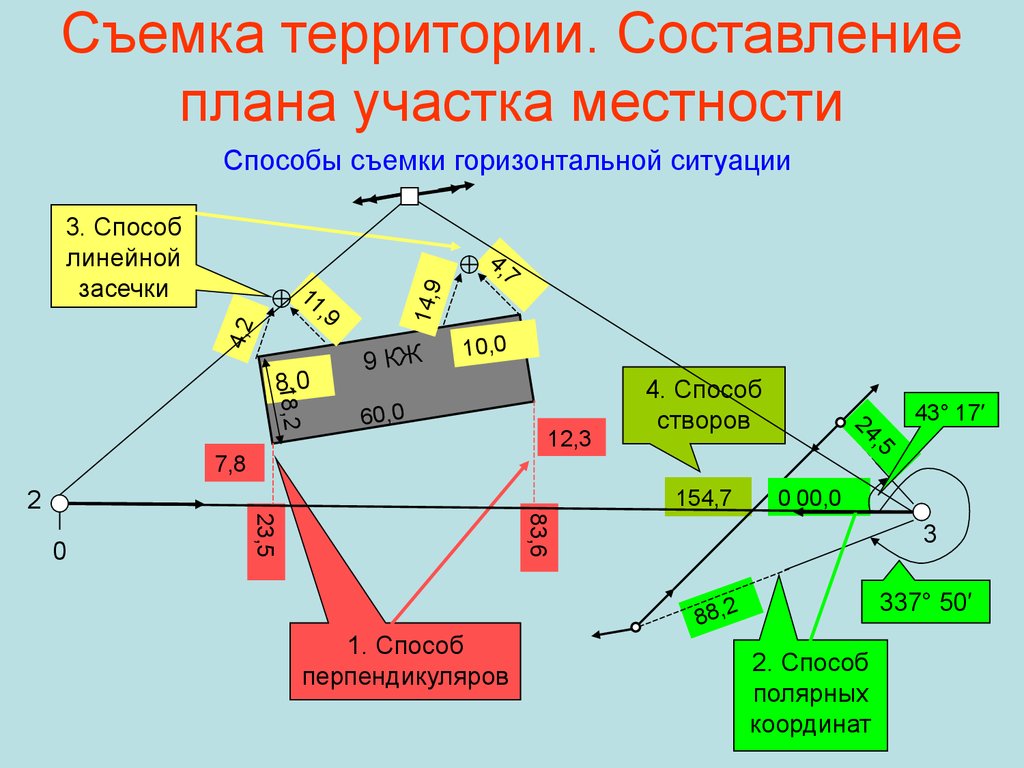
38. Съемка территории. Составление плана участка местности

Способы съемки горизонтальной ситуации
3. Способ
линейной
засечки
9 КЖ
10,0
60,0
12,3
4. Способ
створов
43° 17′
,5
24
18,2
8,0
14,9
4,2
11
,9
4,
7
7,8
154,7
0 00,0
83,6
0
23,5
2
3
337° 50′
88,2
1. Способ
перпендикуляров
2. Способ
полярных
координат

39. Съемка территории. Составление плана участка местности

Способы съемки горизонтальной ситуации
Способ угловой засечки
0 квт
2
2
=
U
Опора ЛЭП
высокого
напряжения
319° 20′
40° 59′
0 00,0
2
0 00,0
3

40. Съемка территории. Составление плана участка местности

Камеральные работы
Решение обратной геодезической задачи;
Вычисление горизонтальных углов по результатам полевых измерений;
Вычисление горизонтальных проложений между смежными точками;
Вычисления в ведомости координат:
Исходные данные;
Уравнивание горизонтальных углов;
Вычисление дирекционных углов;
Вычисление приращений координат;
Уравнивание приращений координат;
Вычисление координат точек теодолитного хода.
Вычисления в ведомости геометрического нивелирования:
• Исходные данные;
• Уравнивание превышений
• Вычисление отметок точек нивелирного хода.
Вычисления в журнале тахеометрической съемки:
• Исходные данные;
• Вычисление отметок пикетов.
Составление плана ситуации и рельефа:
• Нанесение ситуации;
• Нанесение пикетов и рисовка горизонталей.

41. Съемка территории. Составление плана участка местности

Обратная геодезическая задача
X
1
X1
r = αА1
d
dA1
XА
А
Y
yА
r
Arctg
пред-посл
y1
Y Y
r Arctg 1 A
A1
X X
1
A
(X
посл
X
X
посл
X
пред
2
2
) (Y
Y
)
пред
посл
пред
Знаки приращений
координат
Yпосл– Yпред
Y
Y
посл
пред
Xпосл− Xпред
Наименование
румба
Формула
дирекционного
угла
+
+
СВ
α=r
+
−
ЮВ
α = 180 – r
ЮЗ
α = 180 + r

42. Съемка территории. Составление плана участка местности

Вычисления в ведомости координат.
Исходные данные:
1. Измеренные горизонтальные углы; 2. Исходный дирекционный угол;
3. Горизонтальные проложения между смежными точками; 4. Координаты исходных точек.
Уравнивание горизонтальных углов:
В разомкнутом теодолитном ходе
угловая невязка равна:
В замкнутом теодолитном ходе так
как αк = αн, то угловая невязка равна:
Допустимая угловая невязка равна:
Поправки в углы вычисляют по
формуле:
[ к н 180 (n 2)];
i
ф
f
180 (n 2);
i
ф
f
t m n;
доп
f
ф
V
.
n
f

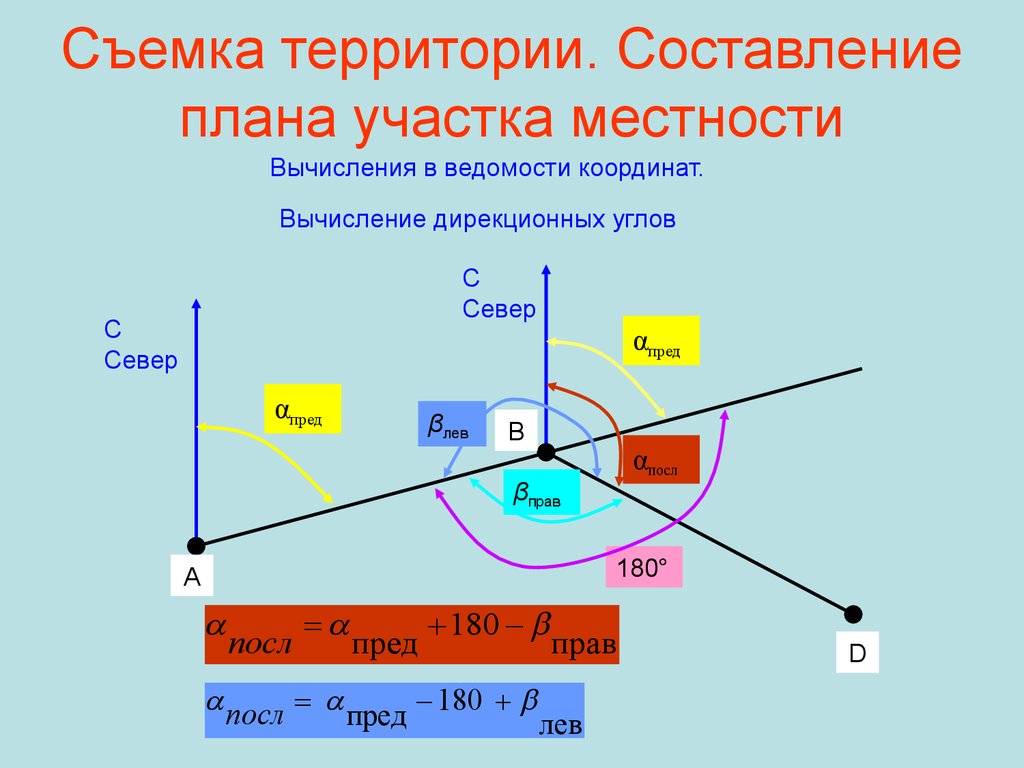
43. Съемка территории. Составление плана участка местности

Вычисления в ведомости координат.
Вычисление дирекционных углов
С
Север
С
Север
αпред
αпред
βлев
В
αпосл
βправ
180°
А
посл
пред
180
прав
посл пред 180
лев
D

44. Съемка территории. Составление плана участка местности

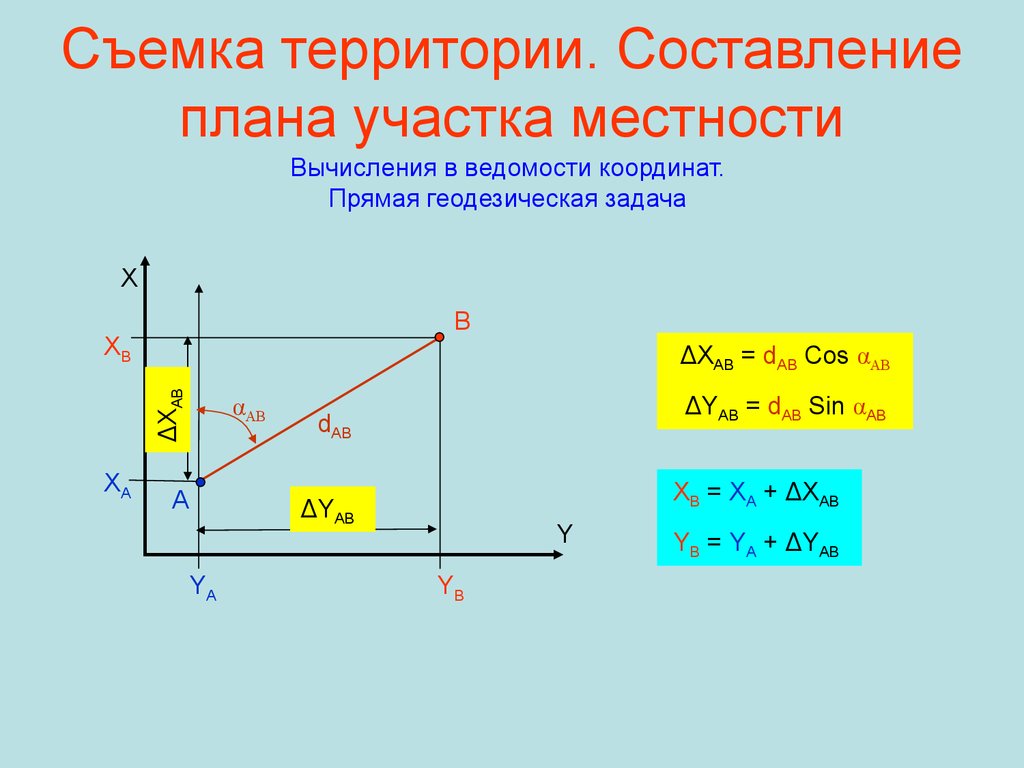
Вычисления в ведомости координат.
Прямая геодезическая задача
X
B
XB
ΔXAB
ΔXAB = dAB Cos αAB
XA
αAB
A
ΔYAB = dAB Sin αAB
dAB
XB = XA + ΔXAB
ΔYAB
YA
Y
YB
YB = YA + ΔYAB

45. Съемка территории. Составление плана участка местности

Вычисление в ведомости координат.
Уравнивание (сторон) приращений координат
fY
X
B
dAB+δd1
∆XAB+δX1
XA
B′
dBC+δd2
∆XBC+δX2
AXY
CXY
XC
∆YAB+δY1
С′
∆YBC+δY2
fX
Y
0
YA
YС
fабс

46. Съемка территории. Составление плана участка местности

Вычисление в ведомости координат.
Уравнивание (сторон) приращений координат
(∆XAB+δX1) + (∆XBC+δX2) = XC - XA;
(∆YAB+δY1) + (∆YBC+δY2) = YC - YA.
δX1 + δX2 = (XC - XA) – (∆XAB + ∆XBC)
δY1 + δY2 = (YC - YA) – (∆YAB + ∆YBC)
fx = -∑δX и
Разомкнутый ход:
Замкнутый ход
fy = -∑δY
fx = ∑∆X – (Xк – Xн);
fy = ∑∆Y – (Yк – Yн),
Если Xк = Xн и Yк = Yн,
то
fx = ∑∆X;
fy = ∑∆Y.

47. Съемка территории. Составление плана участка местности

Вычисление в ведомости координат.
Уравнивание (сторон) приращений координат
Асолютная погрешность –
f
Допустимая погрешность –
f отн
абс
f
2
x
f абс
n
di
f
2
y
1
2000
i 1
Поправки в приращения координат –
Исправленные приращения координат –
f d
x i
v (i ) n
;
x
d
i 1 i
ΔXиспр = ΔXвыч + vx
ΔXиспр = ΔXвыч + vy
Координаты точек теодолитного хода –
Xпосл = Xпред + ΔXиспр
Yпосл = Yпред + ΔYиспр
f d
y i
v
n
y (i )
d
i 1 i

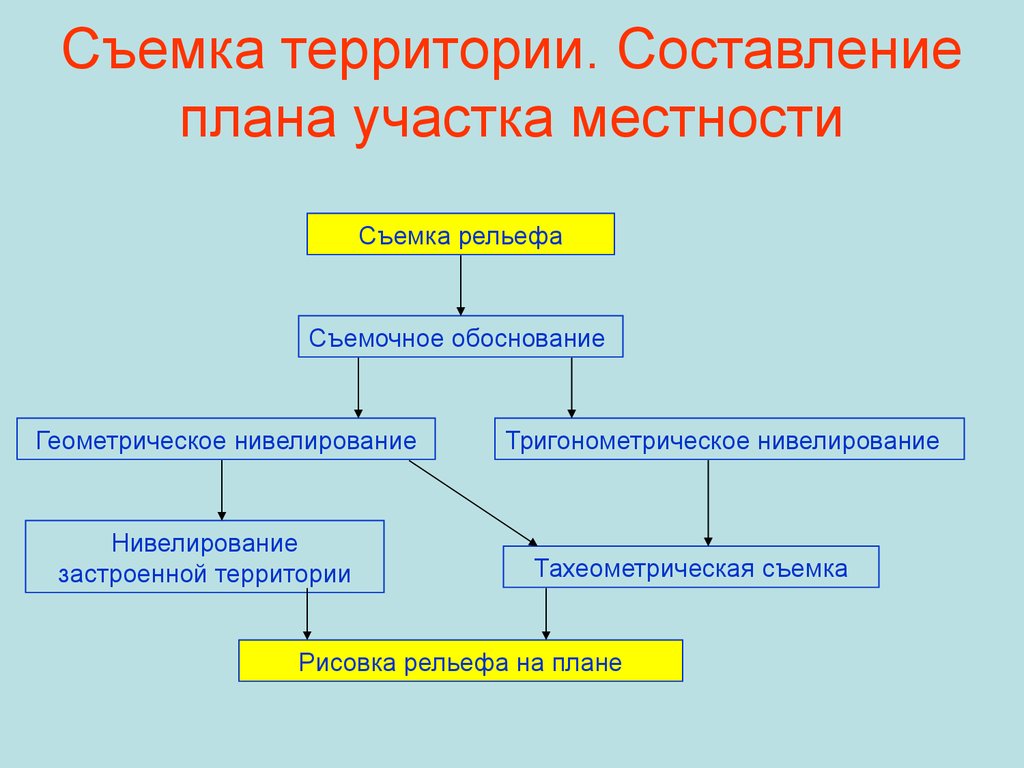
48. Съемка территории. Составление плана участка местности

Съемка рельефа
Съемочное обоснование
Геометрическое нивелирование
Нивелирование
застроенной территории
Тригонометрическое нивелирование
Тахеометрическая съемка
Рисовка рельефа на плане

49.

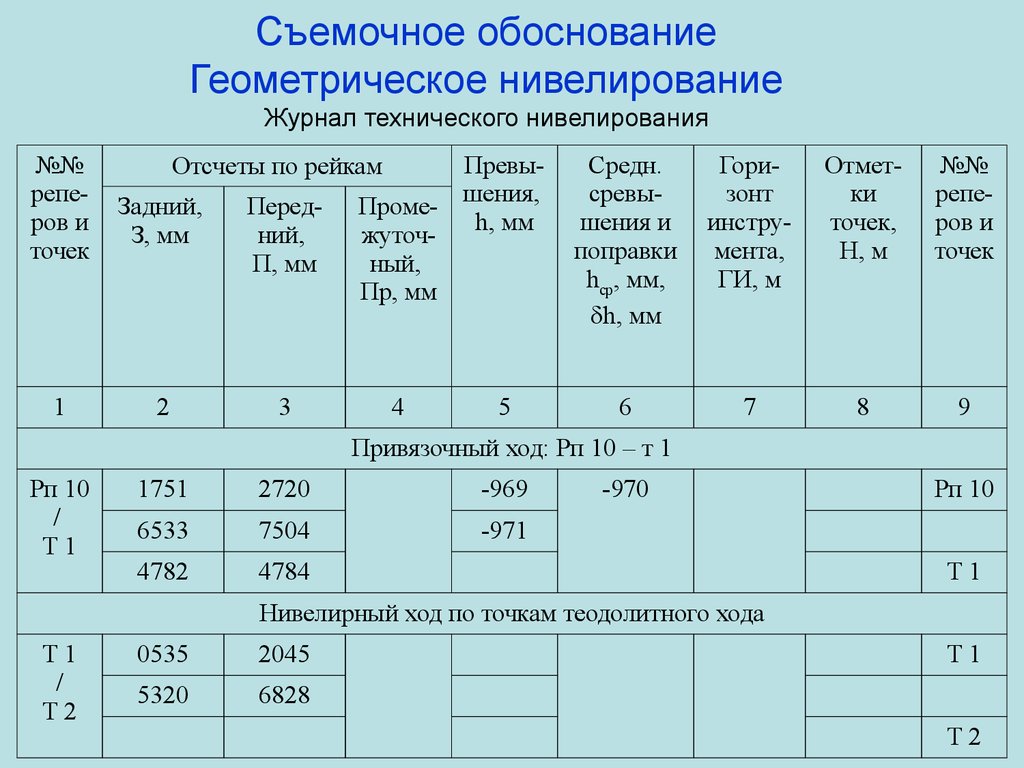
Съемочное обоснование
Геометрическое нивелирование
Журнал технического нивелирования
№№
реперов и
точек
Задний,
З, мм
Передний,
П, мм
1
2
3
ПревыПроме- шения,
h, мм
жуточный,
Пр, мм
Отсчеты по рейкам
4
5
Средн.
сревышения и
поправки
hср, мм,
h, мм
Горизонт
инструмента,
ГИ, м
Отметки
точек,
H, м
№№
реперов и
точек
6
7
8
9
Привязочный ход: Рп 10 – т 1
Рп 10
/
Т1
1751
2720
-969
6533
7504
-971
4782
4784
-970
Рп 10
Т1
Нивелирный ход по точкам теодолитного хода
Т1
/
Т2
0535
2045
5320
6828
Т1
Т2

50.

Съемочное обоснование
Геометрическое нивелирование
Журнал технического нивелирования,
окончание
1
2
3
4
5
6
7
8
9
Привязочный ход: Т 5 – Рп 11
Т4
/
Т5
Т5
/
Рп 11
1173
1738
-565
5958
6523
-565
-565
Т4
Т5
2188
1604
+584
6969
6387
+582
+583
Т5
Рп 11
З
П
Постраничный контроль:
h
З - П =
hср =
З П
2
Сумма средних превышений от репера № 10 до репера № 11 → hср =

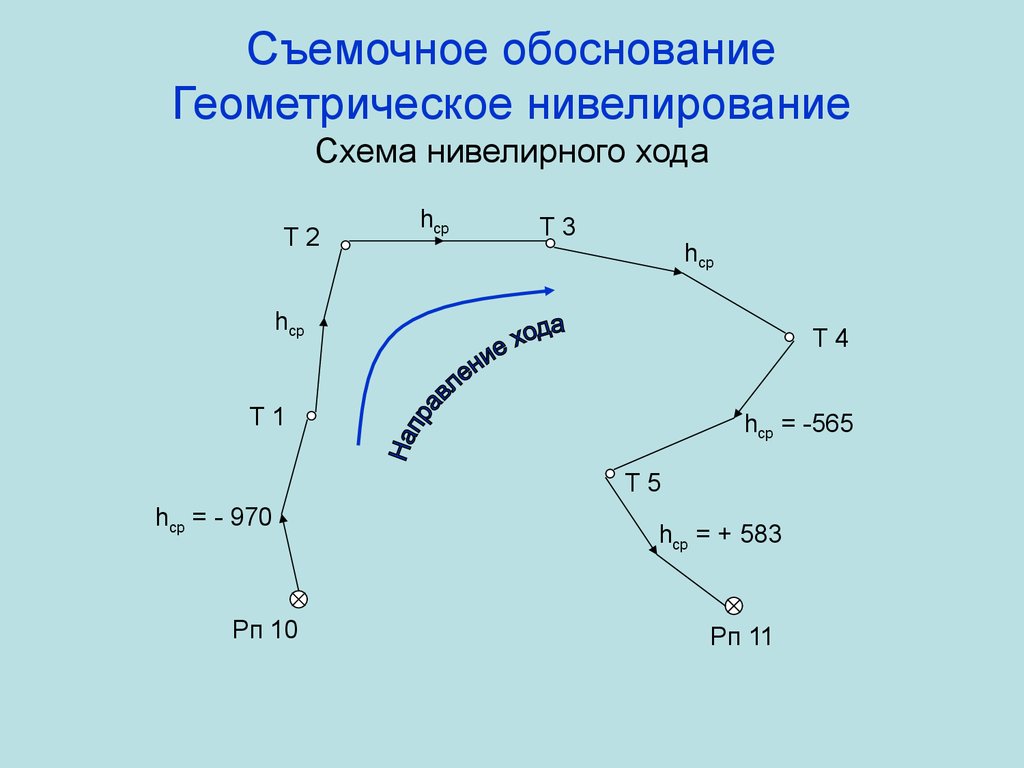
51. Съемочное обоснование Геометрическое нивелирование Схема нивелирного хода

Т2
hср
Т3
hср
hср
Т4
Т1
hср = -565
Т5
hср = - 970
Рп 10
hср = + 583
Рп 11

52. Съемочное обоснование Геометрическое нивелирование Уравнивание превышений

1. Исходные данные:
Средние превышения между станциями
Сумма средних превышений
от репера № 10 до репера № 11
→
Отметки Реперов
→
→
2 Вычисления:
Фактической невязки:
hср
hср
Hрп10
Hрп11
f hф= hср – (HK - HH )
f hф= hср – (Hрп11 - Hрп10 )
50 мм L
Допустимой невязки:
fh(доп) =
Поправок в превышения:
δh = - f hф/ n
Исправленных превышений:
hиспр = hср + δh
Отметок точек:
Hi+1 = Hi + hиспр

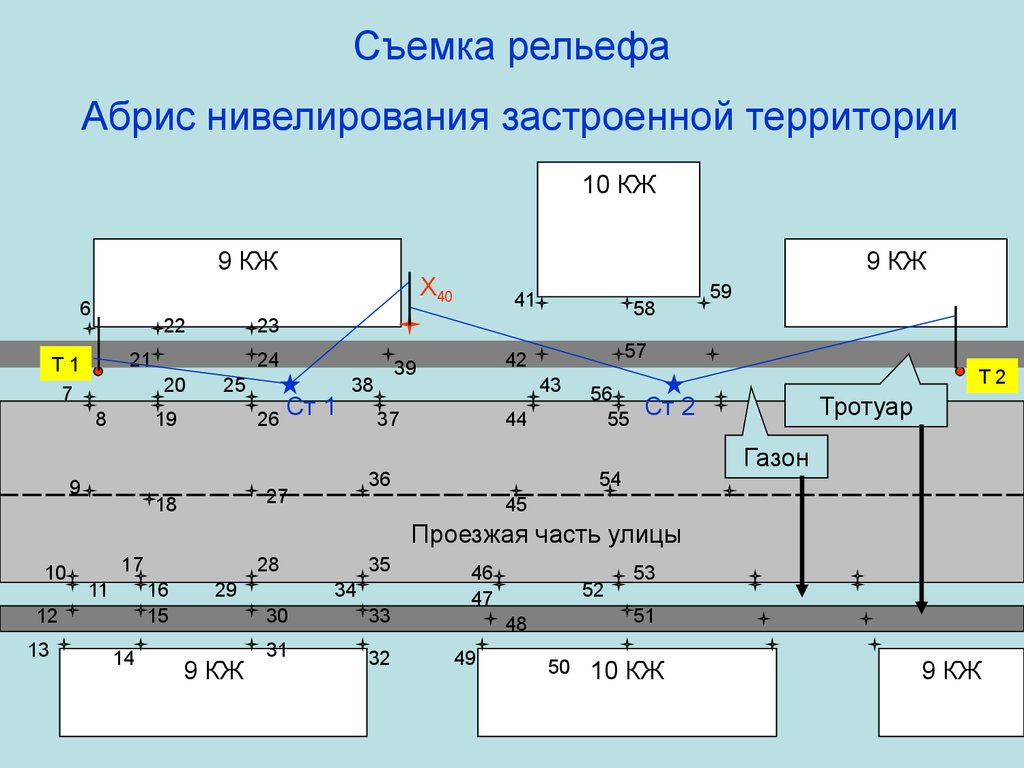
53. Съемка рельефа Абрис нивелирования застроенной территории

10 КЖ
9 КЖ
6
22
24
20
8
25
19
9
X40
41
58
23
21
Т1
7
9 КЖ
26
Ст 1
38
43
37
44
36
27
18
57
42
39
59
56
55
Т2
Ст 2
Тротуар
Газон
54
45
Проезжая часть улицы
10
17
11
16
15
12
13
28
14
29
9 КЖ
35
34
30
33
31
32
46
47
52
51
48
49
53
50
10 КЖ
9 КЖ

54. Съемка рельефа Нивелирование застроенной территории

Журнал нивелирования застроенной территории
Отсчеты по рейкам
ПревыСредн. Горизонт Отметки
№№ Задний, Пере- Промешения,
Сревыш.
инточек,
репе- З, мм
и попр.
струH, м
дний,
жуто h, мм
ров,
hср, мм,
мента,
П, мм
чный,
точек
ГИ, м
Пр, мм
h, мм
и
пикет
1
2
3
Т1
0535
2045
/
5320
6828
X 40
6
7
8
9
…
Нпосл = Нпред + h + h
4
0651
0832
1173
1076
…
55,333 = 56,841 + (-1,509) + 0,001
5
-1510
-1508
6
-1509
+1
7
57,376
8
56,841
№№
реперов,
точек
и
пикет
9
Т1
55,333
X 40
56,725
6
56,544
7
56,203
8
56,300
ГИ = НЗадн + З = 56,841 + 0,535
= 57,3769м
…
…
Нпр = ГИ – Пр = 57,376 – 0,651 = 56,725 м
Нпр = ГИ – Пр = 57,376 – 0,832 = 56,544 м
И так далее

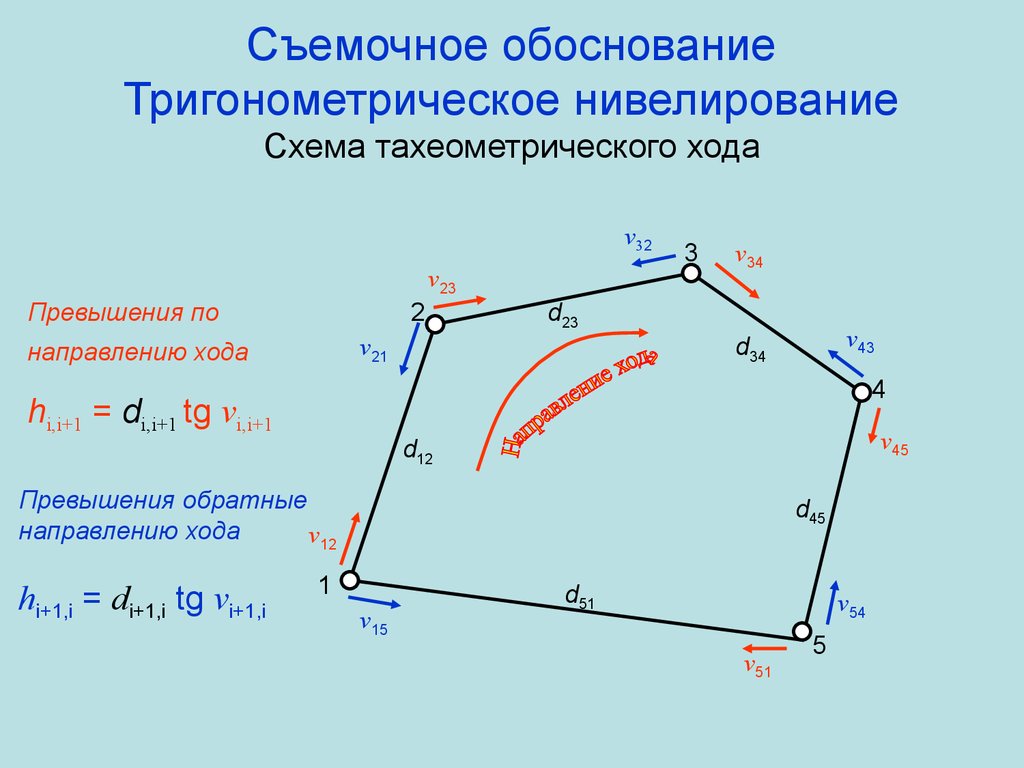
55. Съемочное обоснование Тригонометрическое нивелирование Схема тахеометрического хода

v32
v23
Превышения по
2
v34
d23
4
hi,i+1 = di,i+1 tg vi,i+1
v45
d12
Превышения обратные
направлению хода
v12
hi+1,i = di+1,i tg vi+1,i
v43
d34
v21
направлению хода
3
d45
1
v15
d51
v54
v51
5

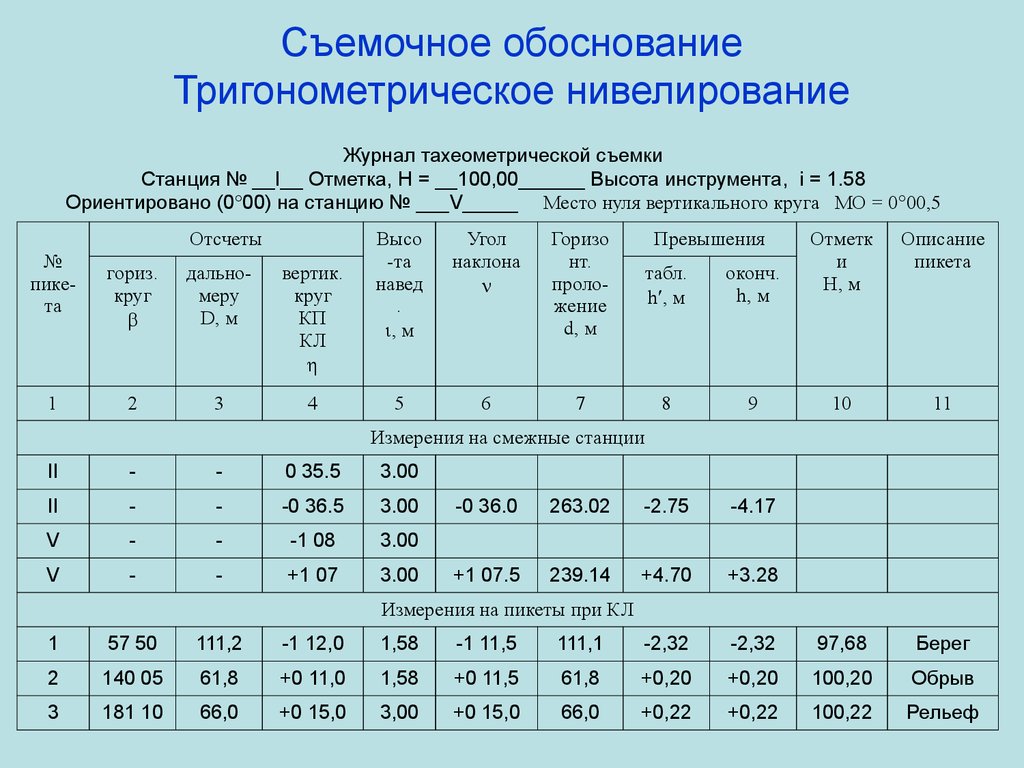
56. Съемочное обоснование Тригонометрическое нивелирование

Журнал тахеометрической съемки
Станция № __I__ Отметка, H = __100,00______ Высота инструмента, i = 1.58
Ориентировано (0 00) на станцию № ___V_____ Место нуля вертикального круга МО = 0 00,5
Отсчеты
№
пикета
1
гориз.
круг
дальномеру
D, м
вертик.
круг
КП
КЛ
2
3
4
Высо
-та
навед
.
, м
Угол
наклона
Горизо
нт.
проложение
d, м
Превышения
табл.
h , м
оконч.
h, м
5
6
7
8
9
Отметк
и
H, м
Описание
пикета
10
11
Измерения на смежные станции
II
-
-
0 35.5
3.00
II
-
-
-0 36.5
3.00
V
-
-
-1 08
3.00
V
-
-
+1 07
3.00
-0 36.0
263.02
-2.75
-4.17
+1 07.5
239.14
+4.70
+3.28
Измерения на пикеты при КЛ
1
57 50
111,2
-1 12,0
1,58
-1 11,5
111,1
-2,32
-2,32
97,68
Берег
2
140 05
61,8
+0 11,0
1,58
+0 11,5
61,8
+0,20
+0,20
100,20
Обрыв
3
181 10
66,0
+0 15,0
3,00
+0 15,0
66,0
+0,22
+0,22
100,22
Рельеф

57. Съемочное обоснование Тригонометрическое нивелирование Ведомость увязки превышений тахеометрического хода и вычисление отметок станци

Съемочное обоснование
Тригонометрическое нивелирование
Ведомость увязки превышений тахеометрического хода
и вычисление отметок станций
№№
Станц.
Расст.
d100
Превышения, м
hпр
hобр
hср
Поправ
-ки, vh,
м
Испр.
hиспр, м
I
Отметки,
H, м
№№
Станц.
100,00
I
II
3,00
-4,17
+4,13
-4,15
-0.04
-4.19
95,81
II
III
2,6
-0,30
+0,26
-0,28
-0.02
-0.30
95,51
III
2,4
+0,90
-0,92
+0,91
-0.02
+0.89
2,7
+6,87
-6,92
+6,90
-0.03
+6.87
96,40
IV
1,9
12,6
-3,24
+3,28
∑hср
-3,26
+0,12
-0.01
-0,12
-3.27
0,00
103,27
V
100,00
I
IV
V
I
∑ d100
fh = ∑hср - ∑hтеор = 0,12 – 0 = +0,12;
0,04 d
100 0,04 12.6 0.22 м
f (доп)
n
h
5
f d
v h 100
h
d100

58. Съемка рельефа Абрис тахеометрической съемки

Съемка на станции I
12
13
На Т II
16
14
V
15
11
10
3
66.0
I
181 10
8
7
9
6
2
.8
1
6
0 00,0
17
57 50
140 05
111.
2
4
5
Р. Соть
1

59. Съемка рельефа Рисовка рельефа на плане

33,45
33,24
33,77
32,17
33,89
31,88
32,19
33,15
34,25
35,77
34,87
34,35
36,45
35,65
36,09
36,59
34,98
33,91
35,97
34,55
37,11
35,18

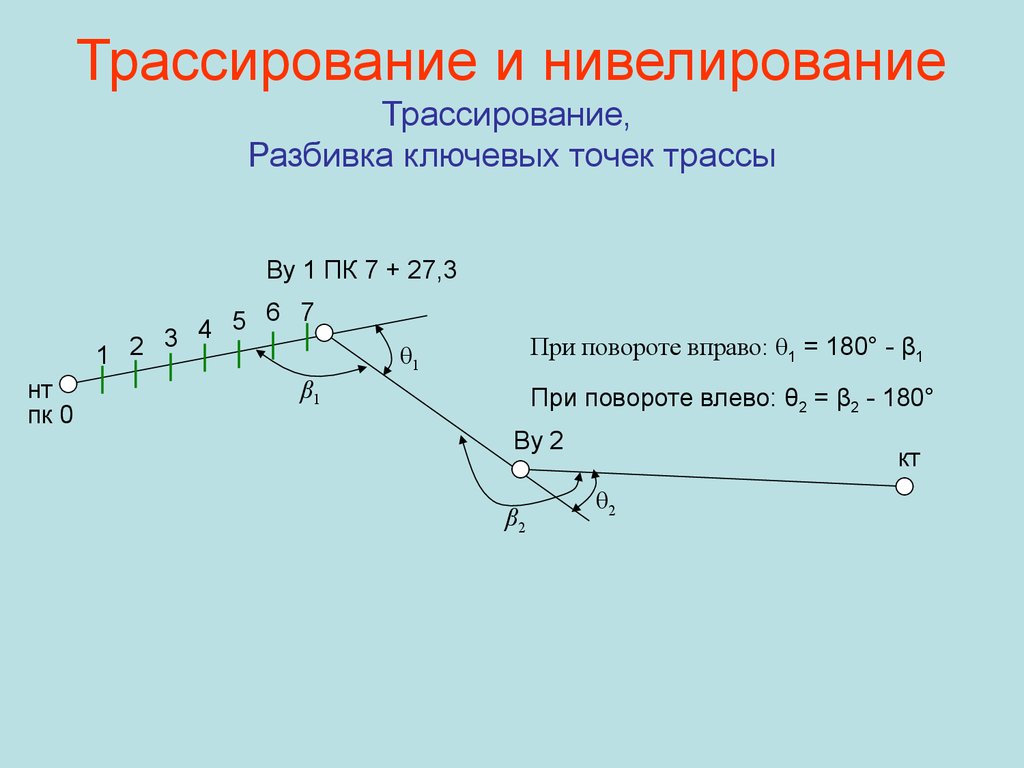
60. Трассирование и нивелирование Трассирование, Разбивка ключевых точек трассы

Ву 1 ПК 7 + 27,3
нт
пк 0
5 6 7
4
3
1 2
β1
При повороте вправо: θ1 = 180° - β1
θ1
При повороте влево: θ2 = β2 - 180°
Ву 2
β2
кт
θ2

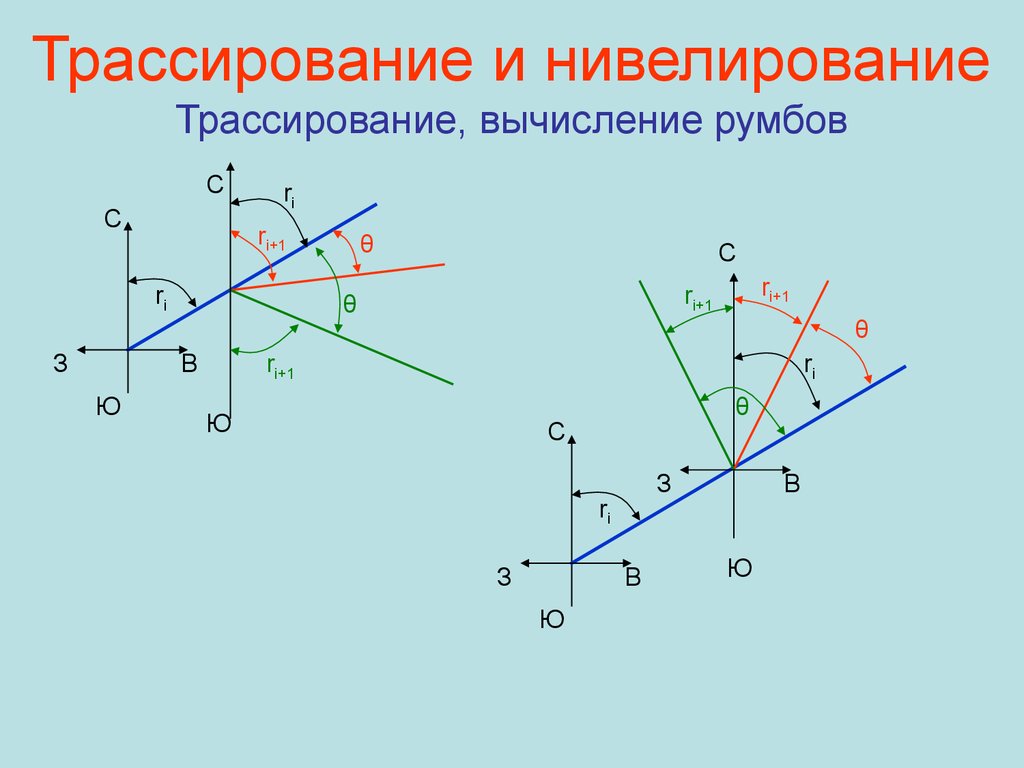
61. Трассирование и нивелирование Трассирование, вычисление румбов

Наименование румба
начальной линии
Угол поворота:
± θ вправо, влево.
Формулы для вычислений
СВ
+ θ вправо
ri+1 = ri + θ,
если ri + θ > 90°,то СВ → ЮВ и ri+1 =180 –(ri +θ)
- θ влево
ri+1 = ri - θ,
если ri - θ < 0°, то СВ → СЗ и ri+1 = θ – ri
ЮВ
- θ вправо
ri+1 = ri - θ,
если ri - θ < 0°, то ЮВ → ЮЗ и ri+1 = θ – ri
+ θ влево
ri+1 = ri + θ,
если ri + θ > 90°, то ЮВ → СВ и ri+1 =180 –(ri+θ)
ЮЗ
+ θ вправо
ri+1 = ri + θ,
если ri + θ > 90°, то ЮЗ → СЗ и ri+1 =180– (ri+θ)
- θ влево
ri+1 = ri - θ,
если ri - θ < 0°, то ЮЗ → ЮВ и ri+1 = θ – ri
СЗ
- θ вправо
ri+1 = ri - θ,
если ri - θ < 0°, то СЗ → СВ и ri+1 = θ – ri
+ θ влево
ri+1 = ri + θ,

62. Трассирование и нивелирование Трассирование, вычисление румбов

C
C
ri
ri+1
ri
З
C
ri+1
ri+1
θ
В
Ю
θ
θ
ri+1
ri
Ю
θ
C
З
ri
З
В
Ю
В
Ю

63. Трассирование и нивелирование Трассирование и разбивка кривой

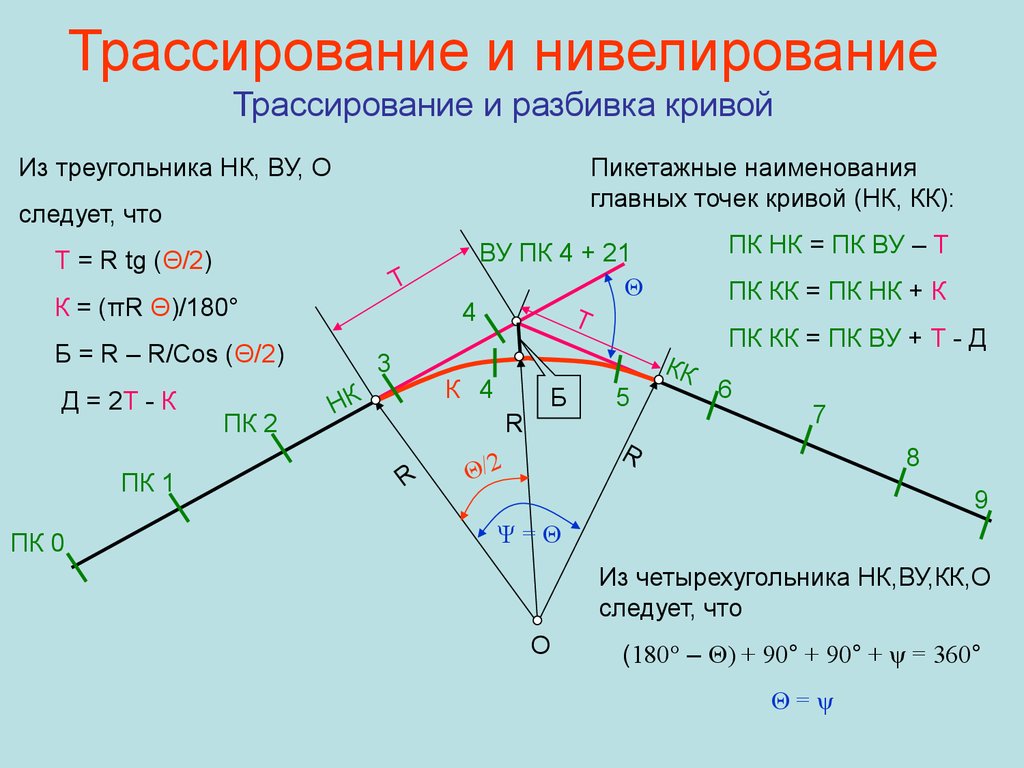
Из треугольника НК, ВУ, О
Пикетажные наименования
главных точек кривой (НК, КК):
следует, что
Т = R tg (Θ/2)
Т
К = (πR Θ)/180°
Б = R – R/Cos (Θ/2)
Д = 2Т - К
ПК 1
ПК 0
ПК 2
3
К 4
НК
Б
R
R
ПК НК = ПК ВУ – Т
ВУ ПК 4 + 21
Θ
4
Т
5
ПК КК = ПК НК + К
КК
ПК КК = ПК ВУ + Т - Д
6
7
R
Θ/2
8
9
Ψ=Θ
Из четырехугольника НК,ВУ,КК,О
следует, что
О
(180° – Θ) + 90° + 90° + ψ = 360°
Θ=ψ

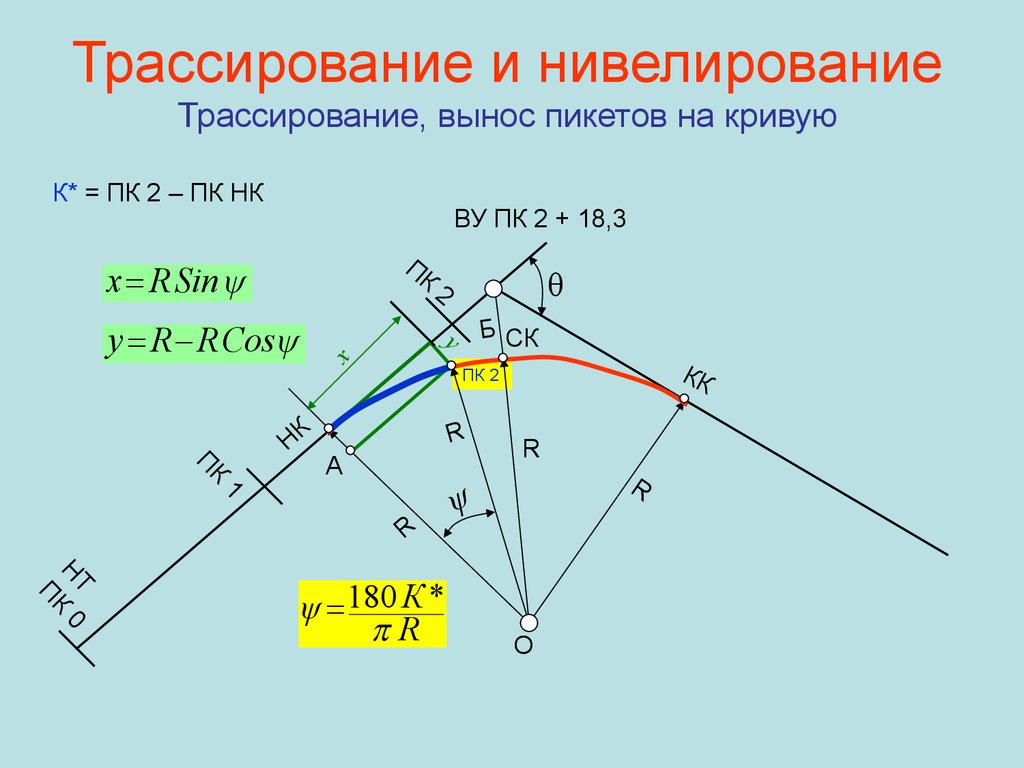
64. Трассирование и нивелирование Трассирование, вынос пикетов на кривую

К* = ПК 2 – ПК НК
ВУ ПК 2 + 18,3
ПК
x R Sin
y R R Cos
Б СК
y
x
НК
θ
2
КК
ПК 2
R
К
П
А
1
R
НТ 0
ПК
ψ 180 К *
R
R
R
ψ
О

65. Трассирование и нивелирование Трассирование, ведомость прямых и кривых

Углы
№
угл
а
Пк
верны
Угол:
+ право
- лево
Кривые
Прямые

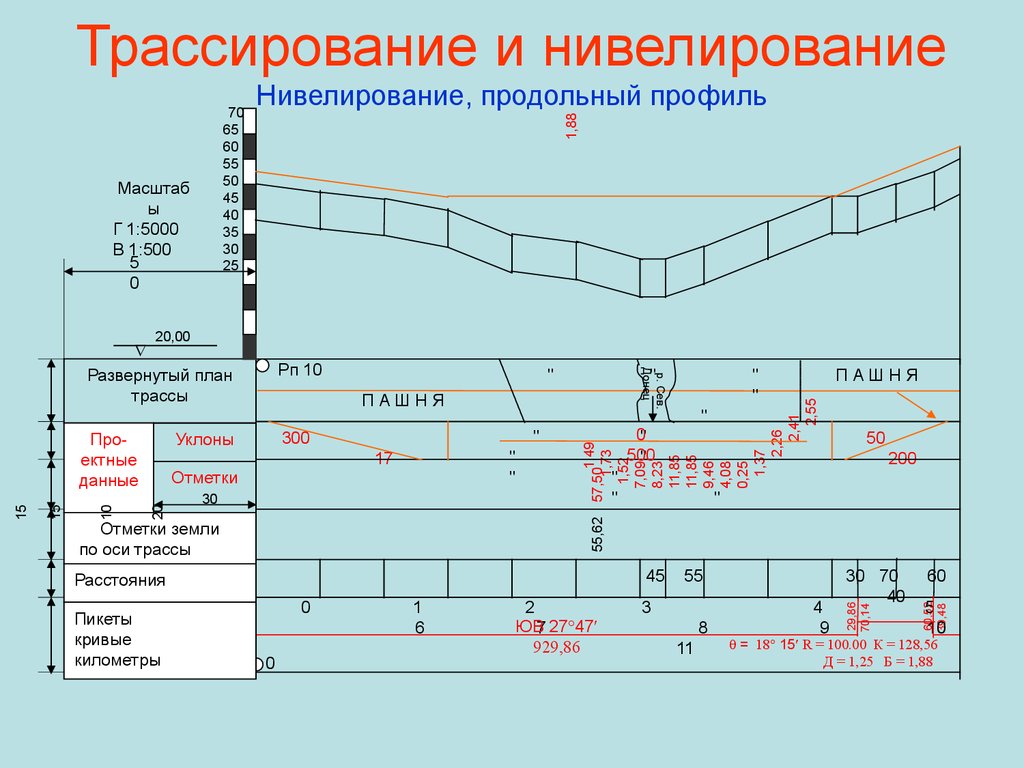
66. Трассирование и нивелирование Нивелирование, продольный профиль

Трассирование и нивелирование
Масштаб
ы
Г 1:5000
В 1:500
5
0
Нивелирование, продольный профиль
1,88
70
65
60
55
50
45
40
35
30
25
20,00
"
"
300
"
"
17
Отметки
ПАШНЯ
"
0"
500
"
"
"
50
200
"
0
0
1
6
2
ЮВ7 27 47
929,86
55
3
8
11
4
9
30 70
40
60
5
10
60,52
39,48
45
Расстояния
29,86
70,14
Отметки земли
по оси трассы
Пикеты
кривые
километры
"
"
55,62
30
"
1,49
57,50
1,73
1,52
7,09
8,23
11,85
11,85
9,46
4,08
0,25
1,37
2,26
2,41
2,55
ПАШНЯ
Уклоны
20
10
15
15
Проектные
данные
Рп 10
р. Сев.
Донец
Развернутый план
трассы
= 18 15 R = 100.00 К = 128,56
Д = 1,25 Б = 1,88

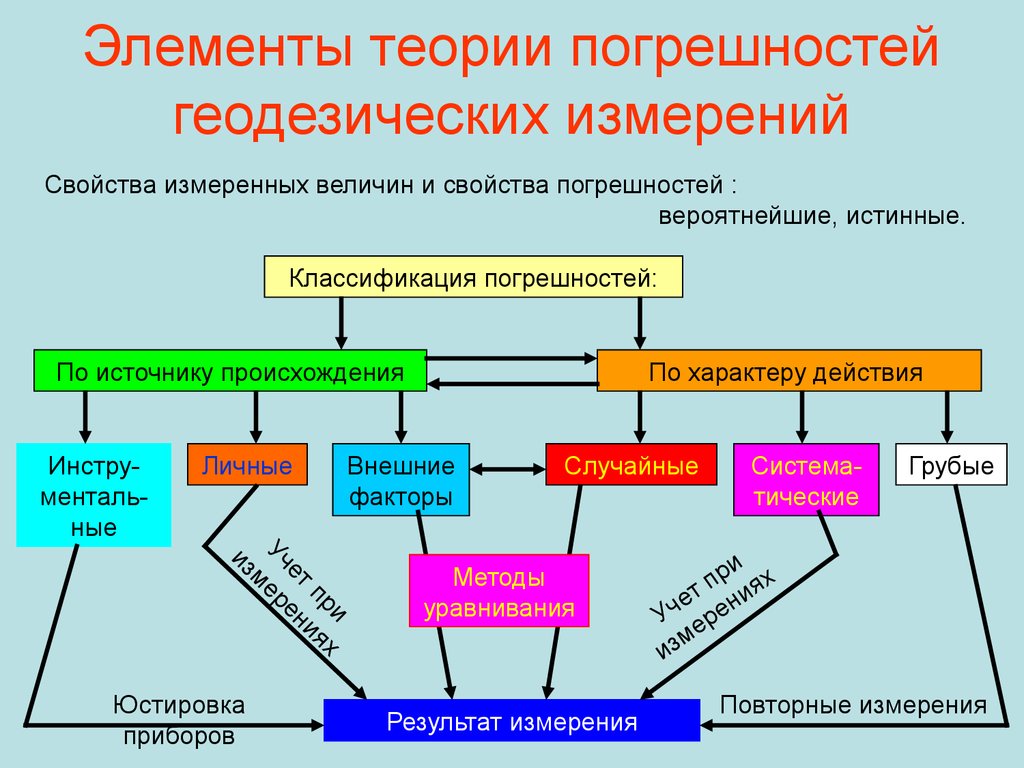
67. Элементы теории погрешностей геодезических измерений

Свойства измеренных величин и свойства погрешностей :
вероятнейшие, истинные.
Классификация погрешностей:
По источнику происхождения
Инструментальные
Личные
из Уче
ме т
ре пр
ни и
ях
Юстировка
приборов
По характеру действия
Внешние
факторы
Случайные
Методы
уравнивания
Результат измерения
Систематические
Грубые
ри х
п
т ния
е
Уч ере
м
из
Повторные измерения

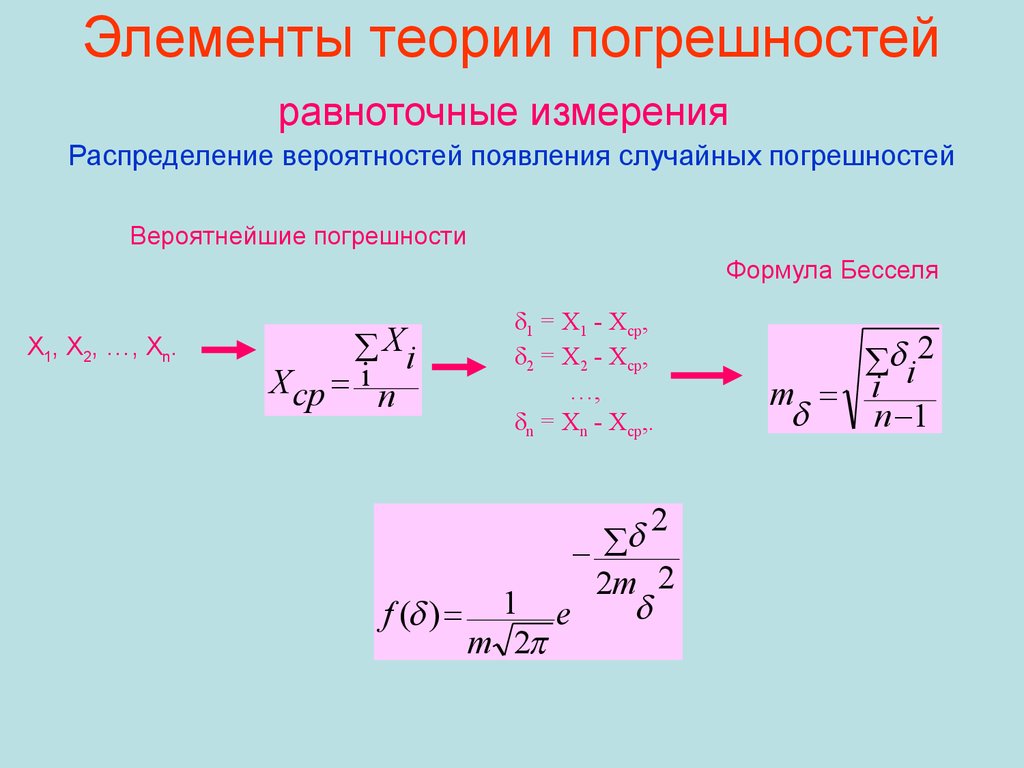
68. Элементы теории погрешностей равноточные измерения Распределение вероятностей появления случайных погрешностей

Вероятнейшие погрешности
Формула Бесселя
X1, X2, …, Xn.
Xi
X ср i n
f ( )
δ1 = X1 - Xср,
δ2 = X2 - Xср,
…,
δn = Xn - Xср,.
1
m 2
2
2m 2
e
i 2
m i
n 1

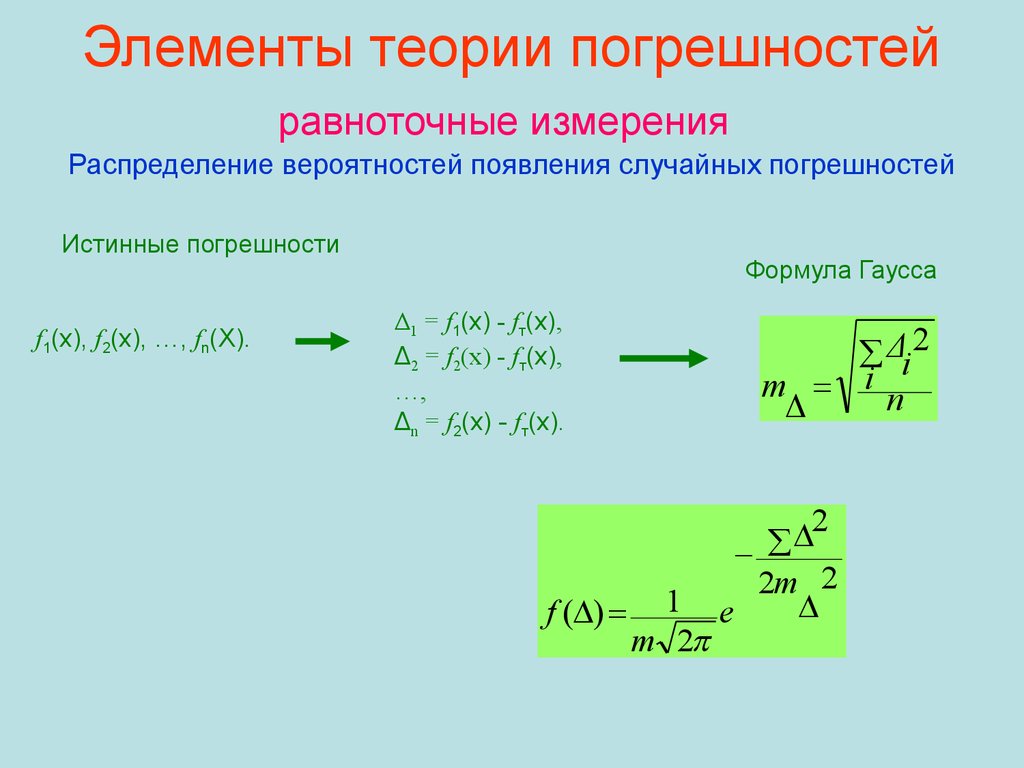
69. Элементы теории погрешностей равноточные измерения Распределение вероятностей появления случайных погрешностей

Истинные погрешности
f1(x), f2(x), …, fn(X).
Формула Гаусса
Δ1 = f1(x) - fт(x),
Δ2 = f2(x) - fт(x),
…,
Δn = f2(x) - fт(x).
f ( )
Δi 2
m in
Δ
1
m 2
2
2m 2
e

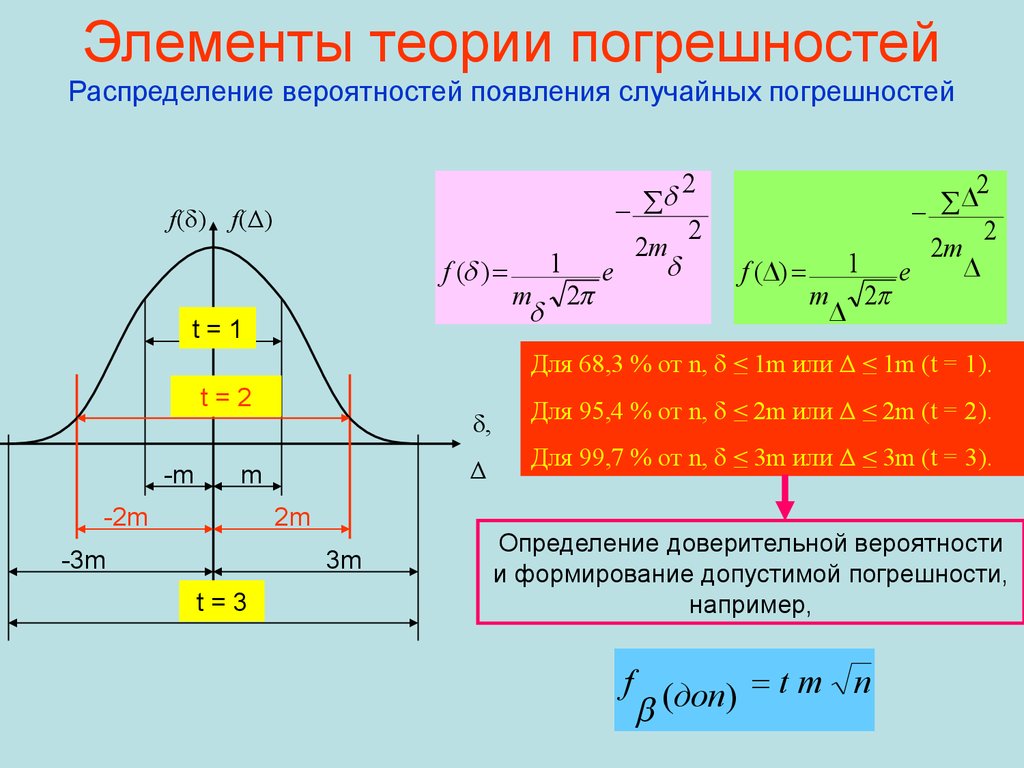
70. Элементы теории погрешностей Распределение вероятностей появления случайных погрешностей

f(δ) f(Δ)
f ( )
t=1
1
m 2
2
2
2m
e
f ( )
1
m 2
2
2
2m
e
Для 68,3 % от n, δ ≤ 1m или Δ ≤ 1m (t = 1).
t=2
-m
δ,
Δ
m
-2m
2m
-3m
3m
t=3
Для 95,4 % от n, δ ≤ 2m или Δ ≤ 2m (t = 2).
Для 99,7 % от n, δ ≤ 3m или Δ ≤ 3m (t = 3).
Определение доверительной вероятности
и формирование допустимой погрешности,
например,
f (доп) t m n

71. Элементы теории погрешностей Случайные погрешности обладают следующими свойствами:

1.
2.
3.
4.
Свойством предельного значения. Абсолютные значения
случайных погрешностей при заданных условиях измерений не
могут превосходить предельного значения. Это предельное
значение является граничным, отделяющим случайные
погрешности от грубых.
Свойством симметрии. Появление отрицательных и
положительных случайных погрешностей равновероятно.
Свойством обратной пропорциональности. Меньшим значениям
случайных погрешностей соответствует большая вероятность их
появления и наоборот, чем больше случайная погрешность, тем
меньше вероятность ее появления.
Свойством компенсации. Среднее арифметическое случайных
погрешностей стремится к нулю при неограниченном увеличении
количества измерений.
i
ср i n 0
при n
или
i
ср i n 0
при n

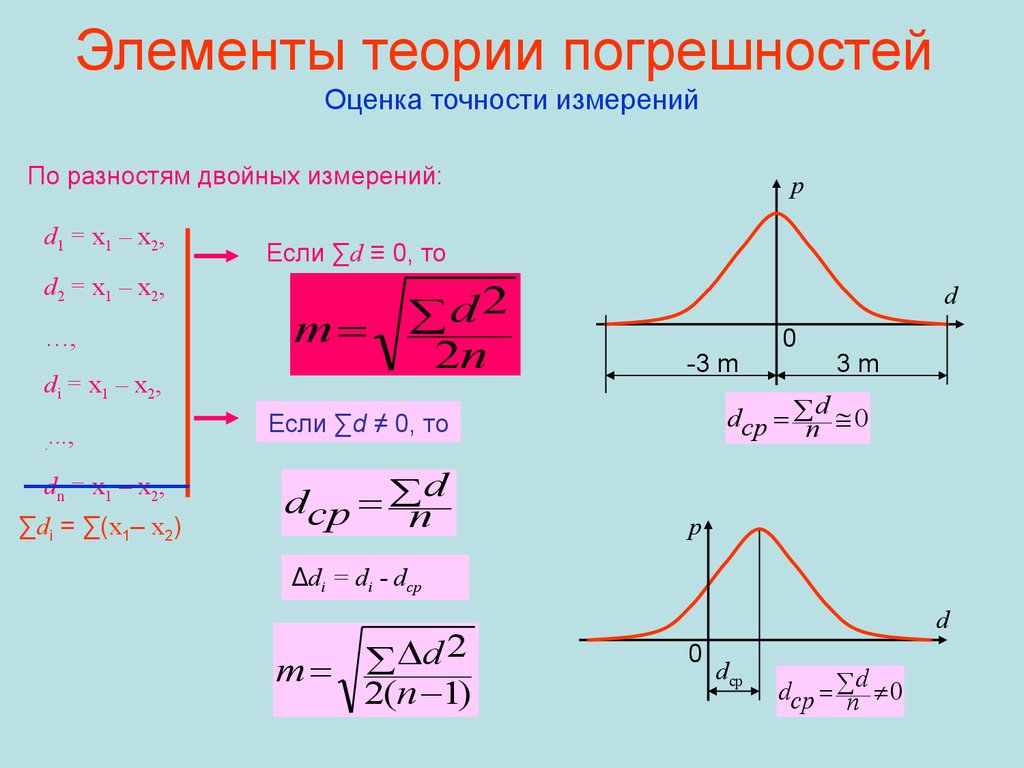
72. Элементы теории погрешностей Оценка точности измерений

По разностям двойных измерений:
d1 = x1 – x2,
d2 = x1 – x2,
…,
di = x1 – x2,
...,
.
dn = x1 – x2,
∑di = ∑(x1– x2)
p
Если ∑d ≡ 0, то
m
d 2
2n
d
-3 m
3m
dср nd 0
Если ∑d ≠ 0, то
dср nd
0
p
Δdi = di - dср
2
d
m
2(n 1)
d
0
dср
dср nd 0

73. Элементы теории погрешностей Оценка точности измерений

Относительная погрешность
f
отн
f
1
абс
d
d
f
абс
1
2000

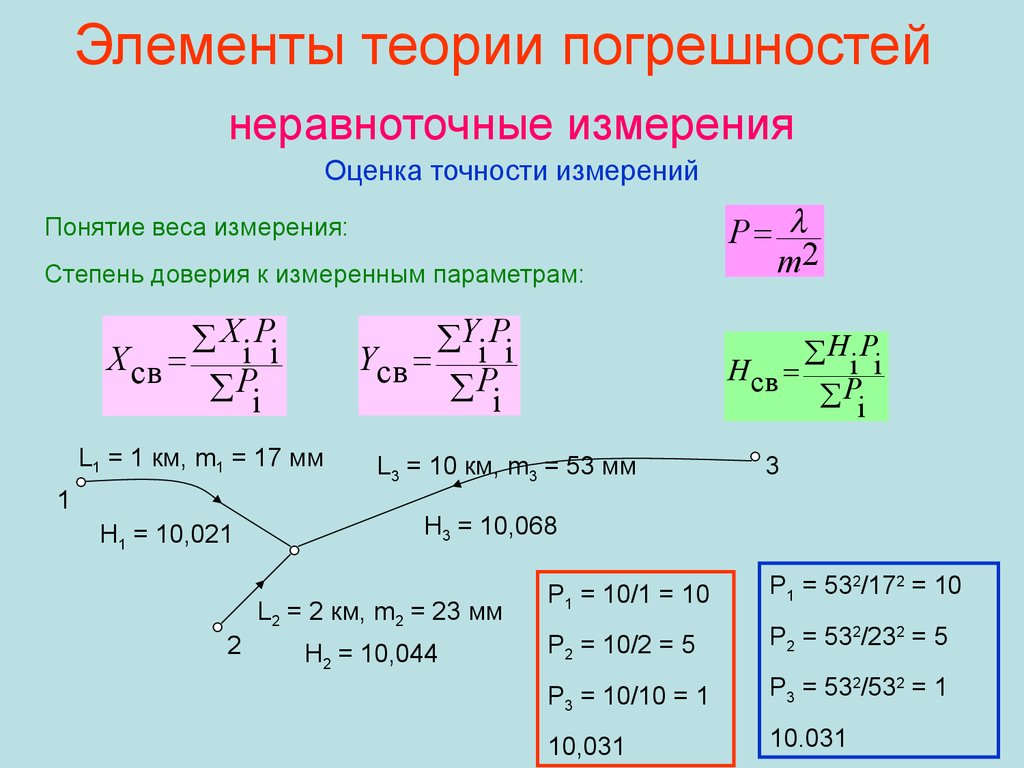
74. Элементы теории погрешностей неравноточные измерения Оценка точности измерений

Понятие веса измерения:
Степень доверия к измеренным параметрам:
Yi Pi
Yсв
Pi
X i Pi
X св
Pi
L1 = 1 км, m1 = 17 мм
1
Н1 = 10,021
Hi Pi
H св
Pi
L3 = 10 км, m3 = 53 мм
3
Н3 = 10,068
L2 = 2 км, m2 = 23 мм
2
P
m2
Н2 = 10,044
P1 = 10/1 = 10
P1 = 532/172 = 10
P2 = 10/2 = 5
P2 = 532/232 = 5
P3 = 10/10 = 1
P3 = 532/532 = 1
10,031
10.031