Similar presentations:
Геодезия. Предмет, задачи и содержание геодезии
1. ГЕОДЕЗИЯ
2. 1.1 Предмет, задачи и содержание геодезии
Геодезия – это наука об измерениях на земнойповерхности.
Задачи геодезии:
- научные;
- научно-технические;
- практические
2
3.
Научные задачи геодезии:- главная научная задача - определение фигуры Земли,
т.е. формы, размеров и гравитационного поля;
- изучение деформаций земной коры;
- изучение перемещения береговых линий морей и
океанов;
- изучение движения полюсов, определение разностей
высот уровней морей и т.п.
К научно-техническим задачам геодезии относятся:
- разработка методов геодезических измерений;
- разработка и выбор типов геодезических приборов;
- разработка методов и приемов математической
обработки результатов измерений.
3
4.
К практическим задачам геодезии относятся:- определение положения отдельных точек земной
поверхности в выбранных системах координат и высот;
- создание карт, планов и профилей;
- производство измерений при изучении, освоении и
охране природных ресурсов;
- производство измерений при проектировании,
возведении и эксплуатации зданий и сооружений
различного назначения.
4
5.
В процессе своего развития геодезия разделилась на ряднаучных дисциплин:
высшая геодезия;
топография;
космическая геодезия;
фотограмметрия;
инженерная геодезия.
5
6. 1.2 Современные представления о форме и размерах Земли
В геодезии для обозначения формы земной поверхностииспользуют термин «фигура Земли».
Знание фигуры и размеров Земли необходимо во многих областях
и прежде всего для определения положения объектов на земной
поверхности и правильного её изображения в виде карт, планов и
цифровых моделей местности.
6
7.
Физическая поверхность Земли представляет собой сочетание суши иводных пространств. Если поверхность Мирового океана почти
ровная, то суша представляет сложное сочетание возвышений и
углублений.
Рисунок 1 – Поверхность Земли
7
8.
Для решения научных и инженерных задач поизучению физической поверхности Земли, а также
других геодезических задач, необходимо:
• определиться с математической моделью
поверхности Земли;
• определить размеры фигуры Земли;
• изучить отступления физической поверхности от
математической.
8
9.
Представления о форме Земли:- шар (сфера);
- сфероид (эллипсоид вращения с малым сжатием);
- трехосный эллипсоид.
В настоящее время за математическую поверхность Земли
принята уровенная поверхность.
Уровенной называют выпуклую поверхность,
касательная к которой в любой точке
перпендикулярна направлению отвесной линии.
9
10.
За основную уровенную поверхность принимают среднююповерхность Мирового океана в состоянии полного покоя и
равновесия, мысленно продолженную под материками (рисунок 1).
Тело, ограниченное основной уровенной поверхностью получило
название геоид (рисунок 2).
Неравномерное распределение масс в земной коре изменяет
направление действия силы тяжести и, следовательно, направление
отвесных линий. Вследствие этого поверхность геоида имеет в
геометрическом отношении сложную форму, не может быть
представлена достаточно простым уравнением и неудобна для
обработки результатов геодезических измерений.
Поэтому там, где это допустимо, поверхность геоида заменяется
приближенными математическими моделями.
10
11.
Рисунок 2 – Геоид11
12.
Из всех геометрических фигур, определяемых относительно простымуравнением, к геоиду ближе всего подходит эллипсоид вращения
(рисунок 3).
Эллипсоид вращения применительно к описанию фигуры Земли
называется общеземным эллипсоидом.
PN
EQ – экваториальная ось
в
а
Е
PnPs – полярная ось
Q
а – большая полуось
в – малая полуось
PS
Рисунок 3 – Эллипсоид вращения
12
13.
Параметры общеземного эллипсоида: большаяполуось – 6 378 136 м, малая – 6 356 752 м, полярное
сжатие - 1/298,2578.
Параметры общеземного эллипсоида установлены на
космических спутниках, ведущих наблюдения за
изменениями на поверхности Земли.
13
14.
Земной эллипсоид с определенными размерами иориентированный определенным образом для части
Земли, называют референц-эллипсоидом.
В нашей стране размеры референц-эллипсоида были
получены под руководством выдающегося геодезиста Ф.
Н. Красовского.
14
15.
Размеры референц-эллипсоида Красовского:EQ
a
6.378.245 м
2
PN PS
b
6.356.863 м
2
а b
1
a
298,3
- большая полуось
- малая полуось
- полярное сжатие
При топографических работах Землю часто принимают за
шар, объем которого равен объему земного эллипсоида.
Радиус такого шара R = 6371,11км.
При геодезических измерениях на площади 20×20 км
уровенную поверхность принимают за плоскость.
15
16.
План местности – это уменьшенное подобное изображениегоризонтальной проекции участка поверхности Земли с
находящимися на ней объектами.
Сферическая поверхность Земли не может быть развернута в
плоскость без складок или разрывов. Изображение Земли на
плоскости, уменьшенное и искаженное вследствие кривизны
поверхности, называют картой.
При составлении карты проецирование производят с искажениями
поверхности за счет влияния кривизны Земли, на плане
изображение получают практически без искажения.
16
17. 1.3 Системы координат, применяемые в геодезии
18.
Топографическое изучение земной поверхности заключаетсяв определении положения ситуации и рельефа
относительно математической поверхности Земли, т.е. в
определении пространственных координат характерных
точек, необходимых и достаточных для моделирования
местности.
Модель местности может быть представлена в виде карт,
планов, а также в виде их электронных аналогов – цифровых
моделей местности (ЦММ) или электронных карт (ЭК).
Для построения моделей местности в геодезии применяют
метод проекций и различные системы координат.
18
19.
Метод проекций и сущность геодезическихизмерений
В геодезии используют ортогональную проекцию,
когда линии проектирования перпендикулярны
плоскости или поверхности, на которую выполняют
проектирование. В геодезии линиями
проектирования являются отвесные линии,
перпендикулярные уровенной поверхности, на
которую проектируют предметы местности, эту
проекцию называют горизонтальной (рис. 4).
19
20.
AB
D
C
A0
D0
А, В, С, D – точки местности;
А0, В0, С0, D0 – горизонтальные
проекции точек местности;
АА0, ВВ0, СС0, DD0 - отвесные линии;
B0
C0
Рис. 4 Проектирование отвесными
линиями
Для определения положения пространственного многоугольника АВСD
необходимо знать величины АА0, ВВ0, СС0, DD0, т.е. расстояния по отвесным
линиям от данных точек местности до уровенной поверхности Земли, эти
расстояния называют высотами точек местности.
20
21.
В тех случаях, когда часть сферической поверхности можно заменитьплоскостью (горизонтальной), касающейся сферы в середине участка,
проектирование выполняют линиями, перпендикулярными к плоскости
Р (рис. 5).
В
h
А d γ
d0
D
С
А0 d0
β1
D0
β4
β2
β3
B0
C0
Р
Горизонтальную проекцию
многоугольника А0В0С0D0 можно
изобразить на плоскости, если наносить
в заданном масштабе длины
горизонтальных проекций А0В0, В0С0,
С0D0, D0А0 и углы β1, β2, β3, β4 между
ними. От измеренной на местности
линии АВ = d переходят к длине ее
проекции:
d0 = dcosν, где
d0 – горизонтальное проложение;
Рис. 5 Проектирование
ν - угол наклона.
перпендикулярами к горизонтальной
плоскости Р
21
22. Влияние кривизны Земли на измерение горизонтальных и вертикальных расстояний
С′А
t
C
Примем фигуру Земли за сферу радиуса
R (рис. 6) и выберем на ней две
произвольные точки А и В.
d – расстояние между точками А и В;
α – центральный угол, соответствующий
дуге d;
t – отрезок касательной АС.
Рис. 6 – Влияние кривизны Земли
В горизонтальном расстоянии между точками А и В возникнет изменение
длины, представленное влиянием кривизны Земли на горизонтальные
расстояния: Δd = t — d,
а в вертикальном направлении — влиянием кривизны Земли на
вертикальные расстояния Δh= ОС— ОВ.
22
23.
d3d
.
2
3R
Приняв R = 6371 км, d = 10км, получим Δd ≈1 см и
Δd: d ≈1:1000000.
Такая погрешность считается допустимой при самых точных
измерениях горизонтальных расстояний на земной
поверхности. С увеличением же d погрешность Δd очень
быстро растет, так как она пропорциональна кубу
расстояний, и при d = 50 км она уже равна 103 см и
Δd:d≈1 : 50 000.
Т. о., в горизонтальной плоскости в пределах площади круга
диаметром 100 км отрезки практически для инженерногеодезических работ сохраняют ту же длину, что и на сфере.
23
24.
1 d2h
.
2 R
Придавая d в формуле различные числовые значения, получим
значения Δh:
d, км
0,5
1
2
3
Δh, см
2
8
31 71
Для инженерных целей высоты точек земной поверхности
необходимо определять с относительно высокой точностью, допуская на 1 км погрешность не более 2-5 см. Отсюда заключаем, что
при измерении вертикальных расстояний нельзя пренебрегать
кривизной Земли даже при сравнительно небольших горизонтальных расстояниях между точками.
24
25. Системы координат, применяемые в инженерной геодезии
В геодезии применяются следующие системы координат:• Географическая (рисунок 7);
• Геодезическая (рисунок 8);
• Плоская прямоугольная геодезическая (рисунок 9);
• Полярная (рисунок 10).
25
26. Система географических координат
Географические координаты используют втех случаях, когда отклонение отвесных
линий от нормали к поверхности не
учитывается (рис.8).
Географическая широта φ равна острому
углу, образованному отвесной линией с
плоскостью экватора.
Географическая долгота λ равна
двугранному углу между плоскостями
начального меридиана и меридиана
данной точки.
Рисунок 7 - Система
географических координат
26
27.
Система геодезических координатРисунок 8 – Система
геодезических координат
Геодезические координаты определяют
положение точки земной поверхности на
референц-эллипсоиде.
Геодезическая широта B – угол, образованный
нормалью к поверхности эллипсоида в данной
точке и плоскостью его экватора. Широта
отсчитывается от экватора к северу или югу от
0° до 90° и соответственно называется
северной или южной широтой.
Геодезическая долгота L – двугранный угол
между плоскостями геодезического меридиана
данной точки и начального геодезического
Гринвичского меридиана.
Долготы точек, расположенных к востоку от
начального меридиана, называются
восточными, а к западу – западными.
27
28. Система прямоугольных координат
С+
х
у
Ось Х всегда направлена на север,
ось Y – на восток
М
х
З
+ В
-
Оси
координат
делят
плоскость горизонта на 4 части,
которые называются четвертями:
I – СВ; II – ЮВ; III – ЮЗ; IV – СЗ.
Ю
Рисунок 9 – Система
прямоугольных координат
28
29. Полярные координаты
О – полюсОР – полярная ось
Для определения
положения точек в данной
системе используют
линейно-угловые
координаты: угол β,
отсчитываемый по часовой
стрелке от полярной
оси ОР до направления на
горизонтальную проекцию
точки А', и полярное
расстояние r от полюса
системы О до проекции А'.
Рисунок 10 – Полярные
координаты
29
30.
Система биполярныхкоординат
М
d1
О1
β1
d2
β2
О2
Рисунок 11 – Система
биполярных координат
В
этой системе
координат два
произвольно избранных полюса О1 и О2,
соединенные прямой – полярной осью –
позволяют определить положение точки М
относительно полярной оси на плоскости при
помощи двух углов β1 и β2 или двух радиусвекторов d1 и d2.
30
31. Система зональных прямоугольных координат Гаусса
Для установления связи между географическими координатами любойточки на земном эллипсоиде и прямоугольными координатами той же
точки на плоскости применяют специальный способ проектирования
всего земного шара на плоскость по шестиградусным зонам,
простирающимся от северного полюса к южному.
В геодезических целях выгодно
применять такое изображение
эллипсоида на плоскости, которое не
искажало бы углов, т.е. углы фигур на
сфероиде и их изображения на
плоскости были бы равными. Такие
проекции называют конформными
(равноугольными).
Рисунок 12 – Деление земного
шара на зоны
31
32. Сущность проекции заключается в следующем:
Из множества возможных равноугольных проекций в РФпринята равноугольная поперечно-цилиндрическая
проекция Гаусса.
Сущность проекции заключается в следующем:
1.
2.
3.
Земной эллипсоид разбивается меридианами на зоны. В России
приняты шести- и трехградусные зоны. Средний меридиан зоны
называется осевым. Нумерация зон ведется от Гринвичского
меридиана на восток.
Каждая зона в отдельности конформно проектируется на плоскость
таким образом, чтобы осевой меридиан изображался прямой
линией без искажений. Прямой линией изобразится также экватор.
Искажения длин линий в проекции возрастают по мере удаления от
осевого меридиана зоны и достигают в шестиградусных зонах
1:1500, а в трехградусных – 1:6000 длины линии.
32
33.
За начало счета координат в каждой зоне принимают точку О – пересечениеизображений осевого меридиана PSPN (оси абсцисс) и экватора EQ (оси ординат).
Абсциссы, отсчитываемые от экватора к северному полюсу, считают
положительными, к южному – отрицательными; значения ординат от осевого
меридиана на восток – положительны, на запад – отрицательны.
X
X
X
X
Х – расстояние от экватора
Y – расстояние от осевого
меридиана зоны
AY
O
6°
O
O
18°
O
Осевой
меридиан
0°
X
12°
1 зона
2 зона
3 зона
4 зона
24°
Y
Экватор
и т.д.
Рисунок 13 – Зональная система прямоугольных координат
33
34.
Система координат в каждой зоне одинаковая. Для установления зоны, ккоторой относится точка с данными координатами, к значению
ординаты слева приписывается номер зоны. Чтобы не иметь
отрицательных ординат, точкам осевого меридиана условно
приписывается ордината, равная 500 км.
34
35.
В РФ координаты Х всегда будут принимать положительные значения (вышеэкватора). Чтобы не иметь отрицательных ординат, точкам осевого меридиана
условно приписывается ордината, равная 500 км.
X
X
600
500
A
400
300
333км
800
700
18°
600
500
400
O
300
12°
900
167км
100
100
0
200
200
Осевой меридиан
…
Экватор
Y
3 зона
Рис.1.15. Определение прямоугольных координат в
системе зональных координат Гаусса
35
36.
Например, координаты Х = 6372км, Y = 4312км означают, что точканаходится на расстоянии 6372 км от экватора, в 4 зоне на
расстоянии 188 км от осевого меридиана зоны.
36
37. Абсолютные и относительные высоты точек земной поверхности
Третьей координатой в геодезии служит высота, определяет положениеточки в пространстве (на физической поверхности Земли).
В геодезии для определения отметок точек применяются следующие
системы высот (рис.15):
• ортометрическая (абсолютная);
• геодезическая;
• нормальная (обобщенная);
• условная.
37
38.
Ортометрическая (абсолютная) высота Hо – расстояние, отсчитываемое понаправлению отвесной линии от поверхности геоида до данной точки.
Геодезическая высота Hг – расстояние, отсчитываемое по направлению нормали от
поверхности референц-эллипсоида до данной точки.
В нормальной системе высот отметка точки Hн отсчитывается по направлению отвесной
линии от поверхности квазигеоида, близкой к поверхности геоида.
Квазигеоид («якобы геоид») – фигура, предложенная в 1950-х г.г. советским учёным
М.С. Молоденским в качестве строгого решения задачи определения фигуры Земли
путем тщательных измерений гравитационного поля Земли.
Рисунок 15 – Высоты точек
38
39.
В нашей стране все высоты реперов государственной нивелирной сетиопределены в нормальной системе высот.
В Российской Федерации началом счета абсолютных высот служит нуль
Кронштадского футштока (горизонтальная черта на медной доске,
установленная в устой моста через Обводной канал), поэтому
применяемую в нашей стране систему высот принято называть
Балтийской.
Рис.16. Кронштадтский
футшток
39
40.
Рисунок 16 – Кронштадский футшток40
41.
Условные высоты определяются относительно условнойуровенной поверхности (рис. 17).
h - превышение
Рисунок 17 – Условная (относительная высота)
41
42. Единые государственные системы координат
Нормативные документы:• Постановление Совета Министров СССР от 07.04.1946г. №760
«О введении единой системы геодезических координат»;
• Постановление Правительства РФ от 28.07.2000г. №568 «Об
установлении единых государственных систем координат»;
• Постановление Правительства РФ от 28.12.2012г. №1463 «О
единых государственных системах координат».
42
43.
ПСМ №760 – СК-42 (построение сети с 19281942гг.)ПП РФ №568 – СК-95, ПЗ-90
ПП РФ №1463 – ГСК-2011, ПЗ-90.11 (+СК-95 и
СК-42 до 01 января 2017г.)
43
44.
Таблица 1 – Параметры эллипсоида в единых государственных системах координатСистема координат Большая полуось а,
м
Полярное сжатие α
Название
эллипсоида
референцэллипосид
Ф.Н. Красовского
СК-42
6378245,0
1/298,3
СК-95
6378245,0
1/298,3
ПЗ-90
6378136,0
1/298,257839
ПЗ-90.11
6378136,0
1/298,25784
ГСК-2011
6378136,5
1/298,2564151
общеземной
эллипсоид
44
45.
Для выполнения кадастровых съемок, при межеванииземельных участков, инвентаризации городских земель,
производстве инженерных изысканий и других видах работ
используются местные системы координат (МСК),
действующие на территории того или иного субъекта РФ.
45
46. 1.4 Ориентирование линий
Карты и планы составляют так, что их верхние края являютсясеверными. Для этого при измерениях на местности линии
ориентируют относительно исходного направления.
Исходными направлениями в геодезии являются: истинный
(географический) меридиан, магнитный меридиан или ось
абсцисс прямоугольной системы координат плана.
В качестве углов, определяющих направление линии, служат
истинный и магнитный азимуты, дирекционный угол и румбы.
46
47.
СAи
М
MN – прямое направление
Рисунок 16 – Определение
истинного азимута
N
Угол между северным
направлением меридиана и
направлением данной линии
называется азимутом.
Измеряется по направлению
движения часовой стрелки, и
может иметь значения от 0◦ 360◦. Азимут, измеряемый
относительно истинного
меридиана, называется
истинным (рисунок 16).
Истинные азимуты линий местности
определяются путем
астрономических наблюдений
или с помощью приборов –
гиротеодолитов.
47
48.
СAи
δ
Aм
Ист. меридиан
М
Угол между северным
направлением
магнитного меридиана
N
и направлением данной
линии называют
магнитным азимутом.
Магнитный азимут, так
же как и истинный,
Зависимость между
истинным и магнитным
считают по
азимутами:
направлению движения
часовой стрелки, он
АИ = Ам + (±δ)
также изменяется от 0◦–
360◦.
Рисунок 17 – Определение магнитного азимута
Так как магнитный полюс не совпадает с географическим, направление
магнитного меридиана в данной точке не совпадает с направлением
истинного меридиана. Горизонтальный угол между этими направлениями
называют склонением магнитной стрелки δ.
Западное склонение имеет знак «-», восточное – «+».
48
49.
Вычисления азимутов связаны с трудностями, т.к. дляпрямой линии на земной поверхности в разных ее точках
азимут изменяется из-за непараллельности меридианов.
В связи с этим на территории, для которой составляют карту
или план, один из географических меридианов
принимают за осевой, т.е. совмещают его с осью абсцисс
системы прямоугольных координат, и относительно него
ориентируют все линии местности.
49
50.
Угол, отсчитываемый в направлении хода часовой стрелки отположительного (северного) направления оси абсцисс до линии,
направление которой определяется, называется дирекционным.
Дирекционный угол обозначается буквой α и изменяется от 0◦ до 360◦.
Рисунок 18 – Определение
дирекционного угла
50
51.
ХС
Х
N
С
Осевой
меридиан
М
Рисунок 19 – Зависимость между
прямым и обратным дирекционными
углами
Осевой
меридиан
αМN
αNM
MN – прямое направление линии;
NM – обратное направление линии.
Различают прямой и обратный дирекционные углы.
αNM = αMN +180◦
51
52.
-γ+γ
Осевой
меридиан
Осевой
меридиан
γ – сближение меридианов
Сближение меридианов считается
положительным, если северное направление оси
абсцисс отклонено к востоку от истинного
меридиана и отрицательным, если это
направление отклонено к западу.
Западное сближение имеет знак «-»,
восточное – «+».
Рисунок 20 – Определение
сближения меридианов
52
53.
ХС
γ
Aи
N
αМN
М
Осевой
меридиан
Аи = α + (±γ)
α = Аи - (±γ)
Рисунок 21 – Зависимость между истинным
азимутом и дирекционным углом
53
54.
Сrсз r
св
З
В
rюз rюв
Иногда для ориентирования линии
местности пользуются румбами.
Румбом, r называется острый угол
между ближайшим (северным
или южным) направлением
меридиана и направлением
данной линии. Перед численным
значением румба указывают его
направление относительно стран
света: СВ, ЮВ, ЮЗ, СЗ. Румбы
измеряют в градусах от 0◦ до 90◦.
Румбы бывают истинные,
магнитные и осевые.
Ю
Рисунок 22 – Определение румба
54
55. Зависимость между дирекционными углами и румбами
Рисунок 23 – Зависимость междудирекционным углом и румбом
Таблица 2 – Зависимость между
дирекционным углом и румбом
№
четверт
и
I
II
III
IV
Дирекционный
угол
α
0◦– 90◦
90◦– 180◦
180◦– 270◦
270◦– 360◦
Румб
r
CВ: r = α
ЮВ: r = 180◦ - α
ЮЗ: r = α - 180◦
СЗ: r = 360◦ - α
55
56. Прямая и обратная геодезические задачи
При создании съемочного обоснования ориентированиесторон теодолитного хода выполняется при помощи
дирекционного угла.
Для вычисления дирекционного угла линии необходимо
знать прямоугольные координаты начальной и
конечной точек этой линии. Такая задача называется
обратной геодезической задачей.
В геодезии часто приходится передавать координаты с
одной точки на другую. Зная исходные координаты
одной точки А, горизонтальное расстояние ее до
другой d и направление α линии, соединяющей обе
точки, можно определить координаты второй точки В. В
такой постановке передача координат называется
прямой геодезической задачей.
56
57.
Прямая геодезическая задачаХ
С
∆Х
∆Y
α
А
В
d
ХВ
ХA
Y
YА
YB
АВ – одна из сторон разомкнутого
или замкнутого теодолитного хода.
Известны:
d – горизонтальное проложение
линии АВ;
α – дирекционный угол;
ХА, YА – координаты точки А.
Требуется найти координаты второй
точки В (ХВ, YВ).
ХВ – ХА = ∆X
Y В – YА = ∆Y
(1)
Разности ∆X и ∆Y координат точек последующей и предыдущей называются
приращениями координат. Из треугольного прямоугольника АВС находим
∆X = d∙cos α
(2)
∆Y = d∙sin α
57
58.
Так как в этих формулах d всегда число положительное, тознаки приращений координат ∆X и ∆Y зависят от знаков cos
α и sin α. Для различных значений углов α знаки ∆X и ∆Y
представлены в таблице 3.
Таблица 3 – Знаки приращений координат
Приращения
координат
∆X
∆Y
I, СВ
+
+
Номер четверти
II, ЮВ
III, ЮЗ
+
-
IV, СЗ
+
-
Вычислив приращения координат по формулам (2), находят
искомые координаты другой точки из формул (1):
ХВ = ХА +∆X
(3)
YВ = YА + ∆Y
58
59.
Этим способом можно найти координатылюбого числа точек по правилу, вытекающему
из формулы (3): координата последующей
точки равна координате предыдущей точки
плюс соответствующее приращение.
59
60.
Обратная геодезическая задачаИзвестны:
ХА, YА , ХВ, YВ – координаты точек А и В.
Требуется найти:
d – горизонтальное проложение линии АВ;
α – дирекционный угол.
Имея координаты точек А (ХА, YА) и В (ХВ, YВ), находят по формулам (1) приращения
координат ∆X и ∆Y, а из равенств (2) – их отношение:
tgr
Y
X
(4)
По формуле (4 ) находят величину угла r (румб) , а по знакам приращений
определяют четверть, в которой он располагается и переходят к дирекционным
углам α. Найдя α, вычисляют расстояние d при помощи формулы:
X
Y
d
(5)
cos sin
Расстояние d можно определить также по формуле:
d X 2 Y 2
(6)
60
61. Связь между дирекционными углами предыдущей и последующей линий
На рисунке представлена схема определения дирекционных углов сторонтеодолитного хода AB. Известен дирекционный угол исходной стороны α0 и
измерены геодезическим прибором теодолитом углы β1, β2, β3, лежащие
справа по ходу от А к В.
Рисунок 24 – Связь между дирекционными углами предыдущей и
последующей линий
61
62.
Дирекционные углы вычисляют по формуле:αn = αn-1 + 180° – βn
То есть, дирекционный угол последующей стороны равен
дирекционному углу предыдущей стороны плюс 180° и минус
угол, лежащий справа по ходу.
Иногда дирекционные углы вычисляют по углам, лежащим
слева по ходу от А до В (λ1, λ2, …, λn), тогда
αn = αn-1 – 180° + λn .
62
63.
На практике ориентирование выполняют с помощьюдирекционного угла для определения положения
съемочного участка относительно заданной системы
координат.
Рисунок 25 – Ориентирование хода
63
64.
Задания по теме «Ориентирование»1.
2.
3.
4.
5.
6.
7.
8.
Вычислите истинный азимут, если магнитный азимут линии равен 36°20/ и
склонение магнитной стрелки западное 3°40/. (1б)
Вычислите магнитный азимут, если истинный азимут равен 115°55ʹ, склонение
магнитной стрелки западное 5°52ʹ. (1б)
Вычислите истинный азимут, если дирекционный угол равен 170°50ʹ, сближение
меридианов восточное 1°30ʹ. (1б)
Вычислите дирекционный угол, если склонение магнитной стрелки западное 6 °35/,
сближение меридианов западное 1°56/ , азимут магнитный равен 225 °35/. (1б)
Вычислите румб прямого направления, если дирекционный угол обратного
направления равен 352°23ʹ. (1б)
Вычислите дирекционный угол направления ВС, если дирекционный угол
направления АВ равен 122°05ʹ и измеренный правый угол равен 210°20ʹ. (1б)
Вычислите координаты точки В, если известны координаты т.А: ХА = 680,40 м, УА =
510,60 м, расстояние между точками А и В равное 121,23 м и дирекционный угол
линии 345°20/. (2б)
Вычислите дирекционный угол и расстояние между точками А и В, если известны
координаты точек А и В: ХА = 1270,23м, УА = 2724,17м, ХВ = 830,75м, УВ = 2678, 34м.
(2б)
64
65. 1.5 Геодезические измерения
66. 1.5.1 Линейные измерения
В геодезии выполняют линейные, угловыеизмерения и измерение превышений.
Измерения выполняют при производстве
различных геодезических работ: при создании
опорных геодезических сетей, при
трассировании линейных сооружений, в
процессе выполнения разбивочных работ, при
монтаже строительных конструкций и т.п.
66
67.
Способы измерения расстояний:- при помощи механических мерных приборов (ленты, рулетки);
- при помощи нитяного дальномера;
- способом прямого промера по оси (светодальномер, тахеометр);
- наземно-космический.
Отрезки небольших размеров чаще всего измеряют простейшими
мерными приборами: рулеткой, мерной лентой, нитяным
дальномером, оптическими дальномерами.
Большие длины измеряют с помощью свето- и радиодальномеров,
тахеометром, наземно-космическим.
При измерении расстояния наземно-космическим способом нет
необходимости в обеспечении видимости между крайними точками
линии.
67
68. При составлении топографических планов, продольных и поперечных профилей необходимо находить горизонтальные проекции каждой
измеряемой линии.Горизонтальную проекцию d = АС
наклонной линии D = AB можно
получить
из
прямоугольного
треугольника АВС по формуле:
d = Dcosv
68
69.
Нитяные дальномеры используют в большинствесовременных оптических приборов, имеющих сетку
нитей.
Нитяной дальномер состоит из двух дальномерных
штрихов (нитей) сетки нитей и вертикальной рейки с
сантиметровыми делениями, устанавливаемой в точке
местности, до которой измеряют расстояние.
Дальномерные штрихи
69
70.
При изучении принципов измерения расстояний нитянымдальномером целесообразно рассмотреть два случая, когда:
1) визирная ось горизонтальна и перпендикулярна вертикальной оси
рейки;
2) визирная ось наклонна и не перпендикулярна вертикальной оси рейки.
70
71.
Для случая горизонтального положения визирной оси горизонтальноепроложение вычисляют по формуле:
d = Cn = С(а-b)
С – коэффициент нитяного дальномера, принимаемый обычно С = 100 или
С = 200;
п – расстояние между верхним и нижним штрихами нитяного дальномера
d
В
А
a = 1520мм
b = 1375мм
d = 100*(1520-1375) = 14500мм = 14,50м
71
72.
.При угле наклона визирной
оси к горизонту v, можно
получить некоторое условное
(дальномерное) расстояние D.
Зная
угол
наклона
визирной оси к горизонту v,
можно определить искомую
величину
горизонтальной
проекции
d
наклонного
расстояния D:
d D cos 2 v
Рис.26. Схема измерения расстояния
нитяным дальномером при
наклонном положении оси
визирования
D Cn
72
73.
Способ прямого промера по оси используют в тех случаях, когдаисполнитель располагает такими приборами, как электронный
тахеометр или светодальномер.
Для определения неприступного расстояния в этом случае в точке 1
измеряемого отрезка устанавливают прибор (электронный тахеометр
или светодальномер), а в точке 2 - отражатель (рис.27). Определение
неприступного расстояния производят в режиме многократного
измерения с определением х = dср.
Рис.27. Схема определения неприступного расстояния светодальномером
73
74.
По конструкции у нивелира визирная ось всегда занимаетгоризонтальное положение, т.к. зрительная труба жестко
скреплена с корпусом.
У теодолита и тахеометра зрительная труба может
перемещаться по вертикальной оси, в связи с чем измерение
расстояний, как правило, выполняется при наклонном
положении визирной оси. В этом случае, возникает
необходимость в приведении наклонного расстояния к
горизонтальному проложению.
Механическими мерными приборами также измеряются в
основном наклонные расстояния.
В таблице приведены формулы для расчета горизонтального
проложения.
74
75.
Прибор, которым измерено наклонноерасстояние
Формула для расчета
горизонтального проложения
Механический мерный прибор (лента,
рулетка)
Оптический дальномер (теодолит)
Электронный тахеометр
d = Dcosv
d D cos 2 v
d = Dcosv
D – наклонное расстояние; v – угол наклона
75
76.
Наземно-космический способ определения неприступного расстоянияиспользуют в случае наличия у исполнителя приемника спутниковой
навигации «GPS» геодезического класса.
Для этой цели, последовательно устанавливая приемник в точках А и В,
определяют их координаты ХА, YА и ХВ, YВ. Далее, решая обратную
геодезическую задачу, устанавливают искомое расстояние d и, если
необходимо, дирекционный угол направления α.
76
77. Измерение неприступных расстояний (косвенное определение расстояний)
Неприступное расстояние может быть определено одним изследующих способов:
• базисов;
• равных треугольников;
• прямого промера по оси;
• наземно-космическим.
77
78.
Способ базисов состоит в измерениинеприступного расстояния с помощью
прямой угловой засечки.
2 случая:
1) Видимость между точками А и В есть;
2) Видимость между точками А и В
отсутствует.
Рис. 28 – Схема определения
неприступного расстояния
способом базисов (1 случай)
78
79.
Последовательность измерений:-от точки А измеряемой линии строят два базиса
b1 и b2. Базисы измеряют землемерной лентой
или рулеткой дважды и при допустимых
расхождениях в промерах определяют
среднее значение каждого из них.
- измеряют углы при основаниях полученных
треугольников АВС1 и АВС2, соответственно γ1,
α1, и γ 2 , α2
- по теореме синусов дважды определяют
значение искомого неприступного расстояния:
b1 sin 1
x1
;
sin 1
b2 sin 2
x2
.
sin 2
79
80.
Если относительная погрешность между двумяизмерениями не превышает допустимой
(проверяют допустимость по формуле,
приведенной ниже), то окончательно принимают в
качестве искомого результата среднее значение.
x1 x2
1
xср
N доп
80
81.
2 случай. Если между точками А и В видимостьотсутствует
Расстояние d после измерения на
местности базисов b1, b′1, b2, b′2 и углов
β и β′ по теореме косинусов получаем:
d
В
А
d b12 b22 2b1b2 cos
b2
b1
bʹ1
β
С
bʹ2
d b1 2 b2 2 2b1 b2 cos
βʹ
С'
Рис. 29 Схема определения
неприступного расстояния способом
базисов (2 случай)
81
82.
Способ равных треугольников состоит в построении вдоступном месте двух равных прямоугольных треугольника
с взаимно параллельными сторонами, в которых одна из
сторон является искомым недоступным отрезком.
В
Рис.30 Схема определения
неприступного расстояния способом
равных треугольников
А
λ
b Сʹ
С
bʹ
λ
Аʹ
Вʹ
82
83. 1.5.2 Угловые измерения
Угловые измерения производят для того, чтобы определить впространстве взаимное положение точек местности.
Угловые измерения выполняют теодолитом или тахеометром.
Углы:
- горизонтальный;
- вертикальный.
83
84.
Пусть имеем точки А, В иО, одна из которых,
например О, служит
вершиной угла АОВ . На
сторонах угла ОА и ОВ
построим две
вертикальные
плоскости N и Р, а через
его вершину проведем
горизонтальную
плоскость Q.
84
85.
Под горизонтальным углом понимаютдвухгранный угол между вертикальными
плоскостями N и Р (это угол между проекциями
сторон на горизонтальную плоскость).
Горизонтальный угол может принимать значения
от 0° до 360°.
85
86.
Вертикальный угол:- Угол наклона;
- Зенитное расстояние.
Углом наклона ν называют угол в вертикальной плоскости между
горизонтальной линией и визирным лучом, направленным на
наблюдаемую точку.
Зенитным расстоянием z называют угол в вертикальной плоскости между
отвесной линией и визирным лучом, направленным на наблюдаемую
точку. Зенитное расстояние дополняет угол наклона до 90°:
z = 90° - ν.
МZ
z
+ν
МО
-ν
z
86
87.
Для получения величины угла наклона или зенитногорасстояния необходимо знать место нуля вертикального круга МО, или место зенита - MZ.
Местом нуля МО называют отсчет по вертикальному кругу
теодолита при горизонтальном положении визирной оси трубы.
Местом зенита MZ называют отсчет по вертикальному кругу
теодолита при положении визирной оси трубы, направленной в
зенит.
87
88. 1.5.3 Измерение превышений (нивелирование)
Превышение, h – это разность высотных отметок двух точек.h = H A – HB
88
89.
Виды нивелирования:- геометрическое (нивелир);
- тригонометрическое (теодолит, тахеометр);
- барометрическое;
- гидростатическое;
- автоматическое;
- стереофотограмметрическое;
- аэрорадионивелирование;
- спутниковые измерения.
89
90.
Геометрическое нивелированиеПревышение между точками получают как разность отсчетов
по рейкам при горизонтальном положении визирной оси
нивелира.
Два вида геометрического нивелирования:
- «вперед»;
- «из середины».
90
91.
Нивелирование «вперед»b
i
В
ГП
НА
h
НВ
А
Уровенная поверхность
h=i–b
ГП = НА + i
Н В = НА + h
НВ = ГП – b
91
92.
Нивелирование «из середины»b
а
ГП
В
НА
h
НВ
А
Уровенная поверхность
h=а–b
ГП = НА + а
НВ = НА + h
НВ = ГП – b
92
93.
Тригонометрическое нивелированиеПревышение между точками определяют по измеренным
вертикальным углам и расстояниям между точками.
M
d∙tgν
ν
i
d
N
i
l
В
h
MN = d∙tgν
h + l = d∙tgν + i
h = d∙tgν + i – l
НВ = Н А + h
А
93
94.
При производстве измерений электронным тахеометром,превышение рассчитывают по формуле
h= Dsinv+ i – l,
где D – наклонное расстояние
94
95.
Барометрическое нивелированиеВ точках местности, находящихся на разных высотах над
уровенной поверхностью, атмосферное давление различное.
Не требуется взаимная видимость между точками.
Выполняется с помощью барометров.
95
96.
Гидростатическое нивелированиеОсновано на свойстве жидкости в сообщающихся сосудах
находиться на одном уровне.
H = (d2 – c2) – (d1 – c1) = K – (c2 – c1)
K = (d2 – d1) – для данной пары сосудов является постоянной
величиной.
96
97.
Автоматическое нивелированиеВыполняется нивелирами-автоматами, установленными на
автомашинах, велосипедах и т.п., которые вычерчивают
профиль нивелируемой линии местности.
Отметки точек можно определить быстро, но с невысокой
точностью.
97
98.
Стереофотограмметрический методВыполняют на стереофотограмметрических приборах.
В настоящее время используются цифровые снимки
местности, специализированное ПО.
98
99.
АэрорадионивелированиеПревышения определяют с помощью радиовысотомеров,
лазерных высотомеров и статоскопов, установленных на
самолетах (реже вертолетах).
99
100.
Определение превышений по результатамспутниковых измерений
2 основные спутниковые системы:
1) ГЛОНАСС – ГЛОбальная НАвигационная Спутниковая Система
(Россия);
2) GPS – США.
100
101. 1.6 Государственные геодезические сети
102. Понятие о ГГС
Геодезическая сеть — система закрепленных на земнойповерхности точек – геодезических пунктов, положение
которых определено в общей системе координат.
Геодезические сети строят исходя из общего принципа геодезии
— от общего к частному.
Все геодезические работы производят с обязательным
контролем для исключения грубых ошибок и для оценки
точности производимых измерений.
Службы:
• Высшее геодезическое управление (ВГУ);
• Главное управление геодезии и картографии;
• Федеральная служба государственной регистрации, кадастра
и картографии (Росреестр).
102
103.
ГГС:- плановые;
- высотные;
- планово-высотные.
По назначению и точности:
- государственные (ГГС);
- сети сгущения;
- съемочные сети;
- сети специального назначения.
103
104.
Точную геодезическую сеть, имеющую координаты,распространяемые на всю территорию страны и являющуюся
основой для построения других сетей, называют государственной
геодезической сетью (ГГС).
Сеть, полученную в результате развития между пунктами ГГС и
связывающую их со съемочными сетями, называют геодезической
сетью сгущения.
Геодезическую сеть, создаваемую для непосредственного
производства топографических съемок, для геодезического
обеспечения инженерных работ и решения других научных и
практических задач, называют съемочной геодезической сетью.
Наряду с ГГС для решения некоторых ведомственных задач могут
создаваться геодезические опорные сети специального
назначения. Обычно это сети повышенной точности и специальной
формы.
104
105. Основные методы создания геодезических сетей
Плановое положение пунктов геодезическихсетей создают методами:
- триангуляции;
- трилатерации;
- полигонометрии;
- наземно-космическим.
105
106.
Метод триангуляции состоит в создании геодезических сетейиз треугольников, в вершинах которых размещены
геодезические пункты, с измерением всех углов и
некоторых из сторон - базисов (рисунок 32).
Рисунок 32 – Метод триангуляции
106
107.
Метод трилатерации (линейной триангуляции) состоит в созданиигеодезических сетей из треугольников, в вершинах которых
размещены геодезические пункты с измерением горизонтальных
проекций длин всех сторон (рисунок 33).
Рисунок 33 – Метод трилатерации
107
108.
Метод полигонометрии состоит в создании геодезическихсетей путем измерения горизонтальных проекций
расстояний между геодезическими пунктами и
горизонтальных углов между сторонами сети (рисунок 34).
Рисунок 34 – Метод полигонометрии
108
109.
Наземно-космический метод заключается в созданиигеодезических сетей с использованием систем и приборов
спутниковой навигации («GPS»).
Системы спутниковой навигации и современные приемники
«GPS» позволяют быстро определять трехмерные
координаты геодезических пунктов с точностью до долей
сантиметра.
Высотные геодезические сети создавались в основном
методами геометрического и тригонометрического
нивелирования.
109
110. Государственная плановая геодезическая сеть
Рисунок 26 – Схемапостроения плановой ГГС
методом триангуляции:
1 – пункт триангуляции
1-го класса;
2 – пункт триангуляции
2-го класса;
3 – пункт Лапласа;
4 – базисная сторона
110
111.
Триангуляцию 3-го и 4-го классов строят в виде отдельныхсистем (рисунок 35).
Рисунок 35 – Схемы построения триангуляции 3...4-го
классов в виде отдельных систем
111
112. Таблица 4 – Основные характеристики плановой государственной геодезической сети
КлассТриангуляция
Полигонометрия
Трилатерация
S, км
mβ
fβдоп
mS/S
mβ
mS/S
mS/S
1
>20
0,7
3
1/400000
0,4
1/400000
-
2
7…20
1,0
4
1/300000
1,0
1/200000
-
3
5…8
1,5
6
1/200000
1,5
1/100000
1/100000
4
2…5
2,0
8
1/200000
2,0
1/40000
1/40000
S – длина стороны; mβ – средняя квадратическая погрешность измерения угла;
fβдоп – допустимая (предельная) невязка в сумме углов треугольника
(триангуляции); mS/S – относительная средняя квадратическая погрешность
измерения стороны в полигонометрическом ходу, трилатерации и базисной
стороны в триангуляции.
112
113. Государственная высотная геодезическая сеть
Создают методами геометрического и тригонометрическогонивелирования.
Государственная нивелирная сеть позволяет:
- равномерно обеспечивать высотной основой всю
территорию страны;
- упорядочить связь высотной сети с уровнями внешних
морей;
- создать обширную сеть повторного нивелирования для
изучения вертикальных деформаций земной коры по
территории всей страны.
113
114.
Государственныевысотные
(нивелирные) геодезические сети
созданы
методами
геометрического нивелирования
и разделяются на сети I, II, III и IV
классов.
Рисунок 36 – Схема
государственной высотной сети
114
115.
Нивелирная сеть I класса создается нивелированием I класса(высокой точности) с применением высокоточных современных
приборов и методик.
Нивелирные ходы I класса образуют полигоны периметром порядка
800 км и служат основой для высотных ходов II класса.
Нивелирные ходы II класса прокладывают внутри сети I класса, как
правило, вдоль железных и автомобильных дорог, при этом они
образуют полигоны периметром порядка 500—600 км.
Нивелирные ходы I и II классов обязательно привязывают к морским
водомерным постам.
Основное назначение нивелирных сетей I и II классов состоит в
создании единой высотной основы на территории страны
(Балтийская система высот). Кроме того, нивелирные сети I и II
классов используют для решения различных научных задач.
Нивелирные ходы II класса сгущают нивелирными сетями III класса,
которые в свою очередь сгущают нивелирными сетями IV класса.
115
116. Разрядные сети сгущения, съемочные сети, сети специального назначения
Разрядные сети сгущения подразделяют на 1-й и 2-й разряды.Триангуляцию 1-го и 2-го разрядов развивают в виде сетей и
отдельных пунктов.
Высотную сеть сгущения создают в основном проложением
ходов технического нивелирования между пунктами
государственной нивелирной сети.
Съемочные сети являются непосредственным геодезическим
обоснованием топографических съемок.
116
117.
Съемочную сеть обычно создают в виде системы теодолитных, теодолитнонивелирных или тахеометрических ходов. Ходы прокладывают междупунктами ГГС и сетей сгущения 1 и 2 разрядов в виде отдельных ходов и
систем с узловыми точками (рис. 37). Длины сторон – от 20 до 350м, а
длины ходов от 0,3 до 6км. Как исключение, допускаются висячие ходы.
Высоты точек съемочного обоснования определяют геометрическим
нивелированием или тригонометрическим нивелированием.
Рисунок 37 – Теодолитные ходы
117
118. Геодезическая основа строительства
Создается с целью:- переноса объекта вертикальной планировки в
натуру;
- выполнения разбивочных работ;
- производства исполнительной съемки
застроенных объектов;
- наблюдений за осадками и деформациями
зданий и сооружений.
118
119.
Геодезическая основа делится на:• плановую;
• высотную.
Пункты нивелирной и плановой разбивочных сетей, как
правило, следует совмещать.
Построение геодезической разбивочной основы для
строительства следует производить методами
триангуляции, полигонометрии, геодезических ходов,
засечек и другими методами.
Плановую разбивочную сеть строительной площадки
следует создавать в виде:
а) красных или других линий регулирования застройки;
б) строительной сетки, как правило, с размерами сторон
50, 100, 200 м и других видов геодезических сетей.
119
120.
Рис. 38 – Схемы разбивочной сети строительной площадки в видеа - строительной сетки; б - красных линий; в - центральной системы
Условные обозначения:
- пункты разбивочной сети строительной площадки; - пункты государственной
геодезической сети;
- строительная площадка; - проектируемые здания
120
121.
Точность построения разбивочной сети строительной площадки (СНиП3.01.03-84)
Характеристика объектов строительства
Величины средних квадратических
погрешностей построения разбивочной сети
строительной площадки
угловые
измерения, с
линейные
измерения
определение
превышения на 1
км хода, мм
Предприятия и группы зданий (сооружений)
на участках площадью более 1 км2; отдельно
стоящие здания (сооружения) с площадью
застройки более 100 тыс. м2
3
1/25000
4
Предприятия и группы зданий (сооружений)
на участках площадью менее 1 км2; отдельно
стоящие здания (сооружения) с площадью
застройки от 10 до 100 тыс. м2
5
1/10000
6
Отдельно стоящие здания (сооружения) с
площадью застройки менее 10 тыс. м2;
дороги, инженерные сети в пределах
застраиваемых территорий
10
1/5000
10
Дороги, инженерные сети вне застраиваемых
территорий; земляные сооружения, в том
числе вертикальная планировка
30
1/2000
15
121
122.
Требования к точности построения внешнейразбивочной сети здания (сооружения), в том числе
вынос основных или главных разбивочных осей также
установлены СНиПом 3.01.03-84.
В соответствии с требованиями к точности следует
осуществлять выбор геодезических приборов и
методы производства геодезических измерений.
122
123.
Создание геодезической основы строительства имеетследующие характерные особенности:
• сети основы создаются чаще всего в условной системе,
с последующей привязкой к государственной
геодезической сети;
• форма сети определяется обслуживаемой
территорией или формой проектируемых объектов;
• сети имеют ограниченные размеры, часто с
незначительным числом фигур и полигонов;
• длины сторон, как правило, короткие;
• для закладки геодезических знаков закрепления сетей
необходимо учитывать сложные условия движения
транспортных средств при начальном этапе
строительства.
123
124. Новая структура ГГС
Основополагающим документом в области создания иразвития ГГС Российской Федерации в настоящее время
являются ГКИНП (ГНТА) – 01 – 006 - 03 «Основные
положения о государственной геодезической сети РФ»
(срок введения в действие 25 июня 2003 г.).
Построение сети основано на применении методов
космической геодезии и использовании глобальных
навигационных спутниковых систем ГЛОНАСС и GPS.
124
125.
Государственная геодезическая сеть, создаваемая всоответствии с настоящими “Основными положениями”,
структурно формируется по принципу перехода от общего
к частному и включает в себя геодезические построения
различных классов точности:
• фундаментальную астрономо-геодезическую сеть (ФАГС),
• высокоточную геодезическую сеть (ВГС),
• спутниковую геодезическую сеть 1 класса (СГС-1).
В указанную систему построений вписываются также
существующие сети триангуляции и полигонометрии 1…4
классов.
125
126.
Расстояние между смежными пунктами ФАГС - 650...1000 км.ВГС представляет собой опирающееся на пункты ФАГС,
однородное по точности пространственное геодезическое
построение, состоящее из системы пунктов, удаленных один
от другого на 150...300 км.
Третий уровень в современной структуре ГГС занимает
спутниковая геодезическая сеть 1-го класса со средними
расстояниями между смежными пунктами около 25…35 км.
126
127.
Рисунок 39 – Схема государственных спутниковых сетей ФАГС и ВГСпо состоянию на 2003г.
127
128.
Рисунок 40 – Схема опорной геодезической сети г. Владимира128
129.
Рисунок 41 – СхемаМосковской городской
геодезической сети
129
130.
Рисунок 42 – Схема сгущениягеодезической сети с применением GNSS
130
131. Способы закладки геодезических пунктов
Положение пунктов геодезической сети обозначают на местностипри помощи специальных сооружений, состоящих каждое из двух
частей: подземной и наружной (надземной).
Наружная часть, называемая геодезическим знаком, представляет
собой сооружение, предназначаемое для установки визирной цели
и подъема измерительных приборов на требуемую высоту над
землей.
В геодезических сетях используют знаки разных конструкций: тур,
простая пирамида, пирамида со штативом, простой сигнал, сложный
сигнал.
Центры геодезических пунктов являются носителями координат.
Поэтому центры должны быть так надежно закреплены на
местности, чтобы была обеспечена их сохранность и стабильность
положения в плане и по высоте в течение длительного времени.
131
132.
Нормативные документы, регламентирующие способызакладки геодезических пунктов и их конструкции:
1. Правила закладки центров и реперов на пунктах
геодезической и нивелирной сетей
2. Инструкция по топографической съемке в масштабах
1:5000, 1:2000, 1:1000 и 1:500 (ГКИНП-02-033-82)
3. Основные положения о государственной геодезической
сети российской федерации (ГКИНП (ГНТА)-01-006-03)
4. Руководство по созданию и реконструкции городских
геодезических сетей с использованием спутниковых
систем ГЛОНАСС/GPS (ГКИНП (ОНТА)-01-271-03)
и др.
132
133.
Конструкции наружных геодезическихзнаков: а) – тур или пирамида; б) – простой
сигнал; в) – сложный сигнал
133
134.
134135.
Геодезический центр и опознавательный столб135
136.
Геодезические пункты,устанавливаемые на зданиях
Геодезический триангуляционный
пункт по ул. Высоцкого на крыше
здания дома №10 г. Самара
136
137.
Стенной знак пункта полигонометрии 2, 3, 4 классов, 1 и 2разрядов. Тип 8 г. р.
137
138. 1.7 Виды топографических съёмок
139. Общие сведения о топографических съемках
Топографической съемкой называют комплекс полевых икамеральных работ по определению взаимного планововысотного расположения характерных точек местности,
выполняемых с целью получения топографических карт и
планов, а также их электронных аналогов — электронных
карт (ЭК) и цифровых моделей местности (ЦММ).
Виды съемок:
- фототопографическая;
- теодолитная;
- тахеометрическая;
- нивелирование поверхности;
- съемка с использованием спутниковой технологии;
- лазерное сканирование.
139
140.
В работе по созданию цифровойкартографической и топографической продукции
руководствуются:
- Инструкцией по топографической съемке в
масштабах 1:5000, 1:2000, 1:1000, 1:500;
- Условными знаками для топографических
планов масштабов 1:5000, 1:2000, 1:1000,
1:500;
- СНиП 11-02-96 (СП 47.13330.2012);
- СП 11-104-97.
140
141.
Топографическая съемка предполагаетследующие виды работ:
- полевые;
- камеральные;
- согласование подземных коммуникаций;
- оформление плана и подготовка отчета.
141
142.
Исходными данными для создания иобновления цифровых топографических планов
являются:
- каталоги координат и высот пунктов
геодезической сети, базовых станций и пунктов
съемочной сети;
- массив точек для формирования цифровой
модели рельефа;
- обзорные картматериалы на район изысканий
и т.д.
142
143.
Съемка:- контурная (ситуационная, горизонтальная);
- топографическая (ситуация и рельеф).
На выбор масштаба влияют так называемые масштаб
образующие факторы, к которым относятся:
- удобочитаемость плана;
- точность изображения рельефа;
- возможность изображения существующих контуров и
элементов проектируемых объектов;
- точность графических данных при проектировании;
- стоимость работ и др.
143
144. Фототопографическая съемка
Фототопографической съемкой называют комплекспроцессов, выполняемых для создания топографических или
специальных карт и планов по материалам фотосъемки.
Снимки могут быть получены различными методами:
• фотографический;
• радио- и звуколокационный;
• рентгеноскопии;
• голографии;
• телевидения и т.п.
144
145.
Аэрофотоснимок145
146.
Радарный снимок146
147.
Панорама по инфракрасным снимкам147
148. Теодолитная съемка
Теодолитная съемка – контурная.Способы съемки ситуации:
- перпендикуляров (рисунок 44);
- линейной засечки (рисунок 45);
- угловой засечки (рисунок 46);
- полярных координат (рисунок 47);
- створов (рисунок 48).
148
149.
CА
В
d6
d3
I
D
d5
II
Е
Рисунок 44 – Способ перпендикуляров
(прямоугольных координат)
149
150.
Рисунок 45 – Способ линейной засечкиРисунок 46 – Способ
угловой засечки
150
151.
Аd1
I
d2
β1
β2
Рисунок 47 – Способ
полярных координат
II
I
S1
Р1
Р2
S2
S3
Р3
S4
Р4
S5
II
Рисунок 48 – Способ створов
151
152.
Абрис152
153. Тахеометрическая съемка
Предназначена для получения топографических планов ицифровых моделей местности (ЦММ).
Плановое положение точек получают методом полярных
координат, высотное – методом тригонометрического
нивелирования.
В настоящее время тахеометрическую съемку выполняют
электронными тахеометрами, позволяющими
автоматически получать превышения и горизонтальные
проложения.
153
154.
IIIII
Лес
березовый
2
1
i
3
β
D
4
5
6
IV
кустарник
VI
V
Рисунок 49 – Схема производства тахеометрической съемки
I – точки съемочного обоснования; 1 – пикеты (реечные точки); i – высота прибора; β –
горизонтальный угол; D – дальномерное расстояние
154
155. Нивелирование поверхности
Основные виды нивелирования поверхности:- по магистралям с поперечниками (рисунок 50);
- вершин квадратов (рисунок 51).
155
156.
Опорой для съемки являетсямагистраль АБ, прокладываемая по
середине участка (рис. 52) или по
границе его.
Перпендикулярно (иногда под
углом к магистрали) разбивают
поперечники (№ 1, №2, №3, № 4).
По магистрали и поперечникам
через равные промежутки закрепляют
точки — разбивают пикетаж.
По пикетажу производят
геометрическое нивелирование.
Рисунок 52 – Нивелирование по
магистралям
156
157.
Рисунок 53 – Нивелирование вершин квадратов157
158.
Нивелирование поверхности по квадратам чаще всего применяется встроительстве при вертикальной планировке участков.
Последовательность нивелирования «по квадратам»:
1. При нивелировании значительных участков вначале разбивают сеть
основных квадратов, сторона которых может быть 100 или 200 м.
2. Основные квадраты разбивают на заполняющие со сторонами 20-40 м,
иногда 10 м, в зависимости от рельефа местности и назначения плана.
3. По сторонам основных фигур прокладывают теодолитные ходы,
опирающиеся на пункты геодезической сети. В результате обработки ходов
получают координаты вершин основных квадратов.
4. Квадраты со стороной 100-200 м нивелируют каждый в отдельности.
Нивелир устанавливают примерно в середине квадрата и производят
отсчеты по рейкам, установленным в его вершинах.
5. Порядок работы в заполняющих квадратах предусматривает нивелирование
с одной станции вершин нескольких квадратов. Высоты вершин
заполняющих квадратов вычисляют через горизонт инструмента
158
159. Съемка с использованием спутниковых технологий
Спутниковые системы:•ГЛОНАСС (Россия);
•NAVSTAR GPS (США).
В результате составляются топографические
карты и планы, цифровые модели местности
(ЦММ) и рельефа (ЦМР).
159
160.
Задачи:• Определение точного местоположения
• Навигация, движение по маршруту с привязкой к карте на
основании реального местоположения
• Синхронизация времени
160
161.
Три сегмента:1. Созвездие ИСЗ - космический сегмент;
2. Сеть наземных станций контроля и управления - сегмент
управления;
3. GPS-приемники - сегмент пользователей.
161
162.
Космический сегментСовременная система GPS и ГЛОНАСС должна состоять из 24
спутников (21 основных и 3 запасных), которые обращаются
на трех орбитах (ГЛОНАСС) и на шести орбитах (GPS). Орбиты
спутников практически круговые и расположены на высотах
19100 км - ГЛОНАСС и 20183 км - GPS.
162
163.
Сегмент управленияГЛОНАСС:
• центр управления системой (ЦУС);
• контрольные станции (КС);
• командные станции слежения (КСС);
• квантово-оптические станции (КОС);
• системы контроля фаз (СКФ);
• аппаратура контроля поля (АКП).
NAVSTAR GPS:
• главная станция управления;
• пять станций слежения
• государственные и частные станции слежения за ИСЗ.
163
164.
Сегмент пользователейСпутниковые приемники по области применения:
1. Геодезические;
2. Навигационные;
3. Приемники времени;
4. Военные.
164
165.
Геодезический приёмник — радиоприёмное устройство дляопределения географических координат текущего
местоположения антенны приёмника, на основе данных о
временных задержках прихода радиосигналов.
165
166. Лазерное сканирование
• воздушное (лидарная съемка);• наземное.
166
167.
При помощи воздушного лазерногосканирования создают сеточные трехмерные
модели местности и объектов местности
(моделей поверхности), 3D модели зданий и
сооружений, застроенных территорий, проводят
обследование электротехнических объектов
(высоковольтных ЛЭП), подстанций и объектов
транспортной инфраструктуры, инвентаризацию
и мониторинг лесов; мониторинг крупных
инженерных объектов, например, открытых
разработок полезных ископаемых и т.д.
167
168.
168169.
169170.
Наземное лазерное сканирование применяется прирешении следующих задач:
• Съёмка фасадов.
• Создание трёхмерных моделей местности, моделей
сложных инженерных сооружений и технологического
оборудования .
• Определение объёмов земляных работ и/или
технологических ёмкостей.
• Контроль строительства мостовых и тоннельных
переходов.
170
171.
171172.
172173.
173174.
174175. 1.8 Цифровые модели местности и рельефа
В памяти ЭВМ данные о местностипредставлены в цифровой форме, в виде
координат X, Y, Н некоторого упорядоченного
множества точек земной поверхности. Такое
множество точек с их координатами образует
цифровую модель местности (ЦММ).
175
176.
Все известные ЦММ можно разбить на три большие группы(рисунок 54):
• регулярные;
• нерегулярные;
• статистические.
176
177.
Рисунок 54 – Виды цифровых моделей местности177
178.
Рисунок 55 –Нерегулярная ЦМР
178
179.
Рисунок 56 – Пример регулярной ЦММ, построенной приобработке цифровых снимков в системе Photomod
179
180.
Рисунок 57 – Пример адаптивной ЦММ, построенной приобработке цифровых снимков в системе Photomod
180
181. 1.9 Геодезические исполнительные съемки
182.
Исполнительные съемки являются способомконтроля геометрических параметров здания или
сооружения, его частей, элементов конструкции и
проводятся для определения:
• фактического (планового и высотного) положения
элементов конструкции и частей здания,
сооружения в ходе строительства и по
завершении строительства;
• отклонений выполненных строительных работ от
проектных;
• объема и качества выполненных работ.
182
183.
Съемку скрытых сооружений (фундаментов,подземных трубопроводов и др.) выполняют
до засыпки землей. Съемка наземной части
здания, сооружения может выполняться
после завершения строительства.
183
184.
Плановое положение отдельных элементов,вертикальность сооружения контролируют с
помощью теодолита или тахеометра.
Исполнительную съемку вертикальной
планировки выполняют нивелированием
поверхности и проложением отдельных ходов по
характерным точкам.
В промышленном и гражданском строительстве
исполнительные съемки производят в масштабе
1:500 или 1:1000.
184
185.
Данные исполнительных съемок конструкцийзданий и сооружений наносят на схемы и
чертежи, на которых указывают фактические
и проектные размеры или величины
отклонений от проектных данных.
185
186.
Рисунок 58 – Пример исполнительной схемы котлована186
187.
Рисунок 59 – Примеры указания действительных отклонений осейэлементов от разбивочных осей на плане: а)- сваи; б) – колонны.
буква «В» для верх него сечения или буква «Н» для нижнего сечения
187
188.
Рисунок 60 – Пример указания невертикальности188
189.
После завершения строительства иблагоустройства территории выполняют
исполнительную съемку контуров застройки
и спланированного рельефа. На ее основе
составляют исполнительный генеральный
план.
189
190.
Исполнительный генеральный план – это комплексдокументов. Например, для большого промышленного
предприятия в его состав входят:
• исполнительный генплан территории М 1:500;
• исполнительные планы отдельных сложных участков
застройки, узлов и установок в масштабе 1:200;
• сводный план инженерных коммуникаций М 1:1000 или
1:2000;
• сводный план (с координатами) зданий и наземных
сооружений М 1:2000;
• технический отчет о геодезических работах,
выполненных на площадке, с приложением
пояснительной записки, схем опорных сетей, каталога
координат и высот пунктов геодезического
обоснования, альбома зарисовок местоположения
геодезических знаков, центров и привязок их к
постоянным предметам местности.
190
191.
На исполнительных схемах могут помещатьсяразличные примечания, согласования
допущенных (измеренных) отклонений с
авторским надзором, а при необходимости,
также разъяснения к условным знакам.
Исполнительные схемы подписываются
геодезистом, ответственным производителем
работ по объекту и руководителем
строительной (монтажной) организации.
191
192. 1.10 Разбивочные работы
193.
Геодезические работы по перенесениюпроектов на местность будем также называть
геодезическими разбивочными работами
(ГРР).
Перенесение проектов на местность
представляет собой процесс, обратный
топографической съемке.
193
194. Элементы геодезических разбивочных работ
проектный горизонтальный угол
проектное расстояние (отрезок)
проектные отметки
линии проектных уклонов
194
195. Построение на местности проектного горизонтального угла
Вβпр.
А
βпр.
КП
βпр.
КЛ
С1
С
С2
При круге КЛ ориентируют
визирную ось теодолита
так, чтобы при
визировании на точку В
отсчет по лимбу
горизонтального круга был
равен 0°00'00". Вращают по
ходу часовой стрелки до
тех пор, пока отсчет по
горизонтальному кругу
теодолита не станет
равным проектному
горизонтальному углу β.
Рисунок 61 – Построение на
местности проектного угла
195
196. Отложение на местности проектного расстояния
Рисунок 62 – Построение наместности проектного расстояния
196
197.
При использовании для построения проектногорасстояния электронного тахеометра построение
проектного расстояния возможно в так
называемом следящем режиме. Помощник
наблюдателя с отражателем постепенно
перемещается по створу линии по направлению
к проектной точке Р. В то же самое время
тахеометром непрерывно измеряют
горизонтальное проложение до отражателя.
Работу выполняют до тех пор, пока на табло
тахеометра не высветится заданное значение
проектного горизонтального проложения. В этом
месте закрепляют знак, фиксирующий
положение точки P на местности.
197
198. Перенесение на местность проектной отметки
Рисунок 63 – Перенесение на местность проектной отметки198
199.
Последовательность (нивелиром):• Вначале на местности находят плановое положение
проектной точки А
• Затем устанавливают нивелир примерно посередине
между исходным репером и вынесенной в натуру
точкой. После этого определяют горизонт прибора по
формуле
ГП = НRp + a
• вычисляют проектный отсчет bпр, который называют
также «проектной рейкой»
bпр = ГП – Нпр
• на местности в точке А забивают кол таким образом,
чтобы отсчет по рейке, установленной на нем, был
равен вычисленному значению bпр.
199
200.
Проектную отметку можно вынести на местностьтакже электронным тахеометром.
• находят плановое положение проектной точки,
которое закрепляют геодезическим знаком.
• Затем электронным тахеометром, который
устанавливают над геодезическим пунктом с
известной высотой, определяют высоту
закрепленной на местности точки, равную H'п. Вычисляют разность hр между проектной отметкой и
найденной высотой
hр = Hпр - H'п,
которую называют условной рабочей отметкой.
плюс - насыпь и минус – выемка
200
201. Перенесение на местность линий проектного уклона
Рисунок 64 – Перенесение наместность линий проектного уклона
нивелиром
1 способ. Наклонным лучом нивелира (рисунок 64). Закрепляют как в плановом, так
и в высотном отношении линию с проектным уклоном АВ.
Устанавливают нивелир примерно посередине линии АВ так, чтобы два его
подъемных винта были направлены вдоль этой линии. Действуя этими винтами ,
добиваются такого положения, чтобы отсчеты v по рейкам, установленным в точках А
и В, были равны между собой. В этом случае визирная ось нивелира будет
параллельна проектной линии.
Полученный отсчет v записывают в журнал и, последовательно перемещая рейку по
точкам 1, 2, 3 и 4, забивают колья на такую высоту, при которой отсчет по рейке будет
равен v.
201
202.
Рисунок 65 – Перенесение наместность линий проектного уклона
нивелиром, теодолитом
Способ Б. В точке А (рис. 65) устанавливают нивелир, теодолит или
тахеометр так, чтобы два подъемных винта подставки были
направлены вдоль линии АВ, и тщательно измеряют высоту прибора i.
Действуя подъемными винтами нивелира или вращая зрительную
трубу теодолита (тахеометра), устанавливают отсчет по рейке в точке
В, равный высоте прибора i, в результате чего визирная ось будет
параллельна проектной линии. Тогда на всех промежуточных точках
забивают колья так, чтобы отсчет по рейке был равен высоте прибора.
202
203. Способы выноса в натуру проектных точек
Исходные данные для перенесенияпроектных точек на местность следующие:
- координаты соответствующих проектных
точек, полученные при проектировании;
- координаты исходных геодезических
пунктов, пункты съемочной сети.
203
204.
Аd1
β1
β2
II
Рисунок 66 – Способ полярных
координат
D
C
В
А
I
d6
d3
I
d2
d5
Е
Рисунок 67 – Способ прямоугольных координат
204
II
205.
Рисунок 68 – Способ прямойугловой засечки
Рисунок 69 – Способ линейной засечки
205
206.
IS1
Р1
Р2
S2
S3
Р3
S4
Р4
S5
II
Рисунок 70 – Способ промеров
по створу
206
207.
Рисунок 71 – Разбивочныйчертеж
207
208. 1.11 Элементы теории ошибок измерений
209. Измерения и их ошибки
Измерением называют процесс сравнения измеряемойвеличины с другой, принятой за единицу измерения
известной величиной.
Всякое измерение производят при наличии следующих
пяти факторов:
1. объект измерения;
2. субъект измерения – наблюдатель;
3. мерный прибор;
4. метод измерения – совокупность правил и приемов при
измерениях;
5. внешняя среда, в которой производят измерения.
209
210.
Измерения:- равноточные;
- неравноточные.
Отклонение результата измерения величины от ее
точного значения называют ошибкой
(погрешностью) измерения.
Погрешности различают:
- грубые;
- систематические;
- случайные.
210
211.
Грубые ошибки или промахи, появляются вследствие недостаточноговнимания наблюдателя или неисправности прибора и приводят к резкому
искажению результатов измерений.
Систематическими
или
регулярными
называют
ошибки,
накапливающиеся по определенному закону с одним знаком. Причины их
возникновения должны быть заранее изучены.
Например, заранее может быть учтено влияние кривизны Земли на
точность определения вертикальных расстояний, влияние температуры
воздуха и атмосферного давления и т.д.
Если не допускать грубых погрешностей и устранять систематические,
то качество измерений будет определяться только случайными
погрешностями, которые неустранимы, однако их поведение подчиняется
законам больших чисел, поэтому их можно анализировать, контролировать и
сводить к необходимому минимуму.
211
212.
Свойства случайных погрешностей:1) для данного вида и условий измерений случайные
погрешности не могут превышать по абсолютной величине
некоторого предела;
2) малые по абсолютной величине погрешности появляются
чаще больших;
3) положительные погрешности появляются так же часто, как и
равные им по абсолютной величине отрицательные;
4) среднее арифметическое из случайных погрешностей одной
и той же величины стремится к нулю при неограниченном
увеличении числа измерений.
212
213.
Разность между результатом измерения некоторой величины lи ее истинным значением Х называют абсолютной
(истинной) погрешностью:
Δ = l – Х.
Отношение абсолютной погрешности измеряемой величины Δ
к самой этой величине l называют относительной
погрешностью:
l
213
214. Арифметическое среднее
l1 l2 ... ln lx
n
n
(7)
- среднее арифметическое
результатов равноточных измерений
одной и той же величины (l1, l2, …,
lп)
X - истинное значение измеряемой величины. Ряд абсолютных
погрешностей измерений:
Δ1 = Х– l1; Δ2 = Х– l2;…; Δп = Х– lп;
(8)
Сложив правые и левые части уравнений (8), получим:
[Δ] = пХ–[ l],
214
215.
откудаl
X
.
n
(9)
n
С увеличением числа измерений
n
будет стремиться к нулю,
и, следовательно, при бесконечно большом числе измерений средняя
арифметическая величина
l
будет равна истинному значению Х.
n
Поскольку на практике число измерений все же ограничено, то среднее
арифметическое будет несколько отличаться от истинного значения
измеряемой величины Х, однако при всяком п арифметическое среднее
считают более надежным значением измеряемой величины.
215
216. Оценка точности результатов непосредственных равноточных измерений
Под точностью измерений понимают качествоизмерений, определяющее близость их результатов к
точному (истинному) значению измеряемой
физической величины.
Для оценки точности ряда измерений существует
несколько критериев.
1. Средняя ошибка (V).
Среднее арифметическое из абсолютных значений
случайных ошибок называется средней ошибкой, т.е.
V = [|∆i|] ⁄ n ,
где [|∆i|] = |∆1| + |∆2| + … + |∆n|
216
217.
2. Вероятная ошибка. Вероятной ошибкойназывается такое значение случайной ошибки,
больше или меньше которого по абсолютной
величине ошибки равновозможны.
Если все ошибки расположить в ряд по
убывающим или возрастающим значениям
абсолютных величин, то вероятная ошибка будет
в середине этого ряда. Поэтому вероятную
ошибку часто называют срединной.
3. Относительная ошибка равна отношению
ошибки измерения к значению измеряемой
величины.
217
218.
4. Средней квадратической ошибкой называется величина,вычисляемая по формуле – корень квадратный из
арифметического среднего квадратов истинных погрешностей:
2
m
Формула Гаусса:
i n
т.е. [ ∆i²]= ∆1² + ∆2² + ∆3 ² +…+ ∆n²
Поскольку истинное значение измеряемой величины Х не
известно, то среднюю квадратическую погрешность т
вычисляют по уклонениям υi отдельных результатов измерений
li от арифметического среднего x:
υi = l i - x
Через уклонения арифметического среднего среднюю
квадратическую погрешность определяют по формуле Бесселя:
m
.
2
n 1
218
219.
5. Предельная ошибка. Величина средней, вероятной илисредней квадратической ошибки, только тогда характеризует
точность измерений, если известно max допустимое значение
этих ошибок при данных условиях измерений. Все измерения
с ошибками > ∆пред отбрасывают как грубые и измерения
повторяются заново.
Для теоретических расчетов ∆пред = 3т, на практике, учитывая
ограниченное число измерений, принимают ∆пред = 2т.
Случайные ошибки, превышающие предельную, считают
грубыми, а результаты измерений, содержащие такие ошибки,
бракуют.
219
220. Оценка точности функций измеренных величин
В практике геодезических работ нередко искомые значенияполучают в результате вычислений как функции измеренных
величин. В этом случае результаты будут содержать ошибки,
значения которых зависят от вида функции и от ошибок
аргумента.
Для функций нескольких независимых величин z =f( x, y,…, t)
определяют по формуле:
2
f 2 f 2
f 2
m z m x m y ... mt .
x
t
y
2
2
220
221.
Таблица 5 – Средняя квадратическая ошибка функцийФункция
Средняя квадратическая ошибка
функции
1. U = k∙x,
где k – безошибочное постоянное число;
x – аргумент, полученный из измерений
mu = k∙mx
2. U = х + у
mu m x2 m y2
mu m x2 m y2
3. U = x-y
4. U = k 1∙x+k 2∙y+…+k n∙w
5. U = x∙y
6. U = x/y
mu k12 mx2 k 22 m y2 ... k n2 mw2
mu m x2 y 2 m y2 x 2
mu
m x2 y 2 m y2 x 2
y4
221
222.
Например, если площадь треугольника была1
вычислена по формуле: Р аh , то средняя
2
квадратическая ошибка определения площади
будет вычисляться по формуле:
1
mP
h 2 ma2 a 2 mh2
2
222
223. Понятие об уравнивании результатов геодезических измерений
Уравниванием называется совместная математическаяобработка измерений, при которой выполняют контроль и
оценку их качества, находят наиболее вероятные значения
измеренных величин (углов, линий, превышений) и их
функций (дирекционных углов, координат, высот).
223
224.
Перед уравниванием измеренных величин выполняется оценкаточности выполненных измерений в следующем порядке:
1.
2.
3.
4.
Определяют невязку по правилу: практическое значение
измеренной величины минус теоретическое (истинное).
Сравнивают полученную невязку с предельно допустимым
значением.
Если полученная невязка меньше допустимого, то значит, что
измерения выполнены с удовлетворительной точностью, находят
поправки и распределяют их в измеренные величины, т.е.
выполняют уравнивание.
Если полученная невязка больше допустимого, то измерения
содержат грубые ошибки, такие измерения устраняют.
224
225.
Рассмотрим процедуру уравнивания на примере оценкиточности угловых измерений в теодолитном ходе.
.
1. Находят угловую невязку теодолитного хода по формулам:
fβ = Σβпр. - Σβтеор.,
где Σβпр. – сумма практическая (сумма измеренных углов в ходе);
Σβтеор. = 180◦ (n-2) – для замкнутого хода;
Σβтеор.. = αнач. – αкон. + 180◦n – для разомкнутого хода;
n – количество горизонтальных углов.
2. Определяют допустимость вычисленной угловой невязки.
fβ ≤ fβдоп.
fβдоп. = 1ʹ √n
225
226.
3. Распределяют невязку поровну на все углы введениемпоправок δβ. Поправки vi вычисляют по формуле
δ β = fβ / n
и вводят с обратным знаком в значения измеренных углов,
получая уравненные углы.
4. Сумма уравненных углов должна быть равна теоретической.
Σβуравн. = Σβтеор.
Пример: Σβпр = 540°01,5ʹ, чему будут равны поправки, если
количество углов в ходе равно 5? Ход замкнутый. Находится ли
величина невязки в допуске?
226



















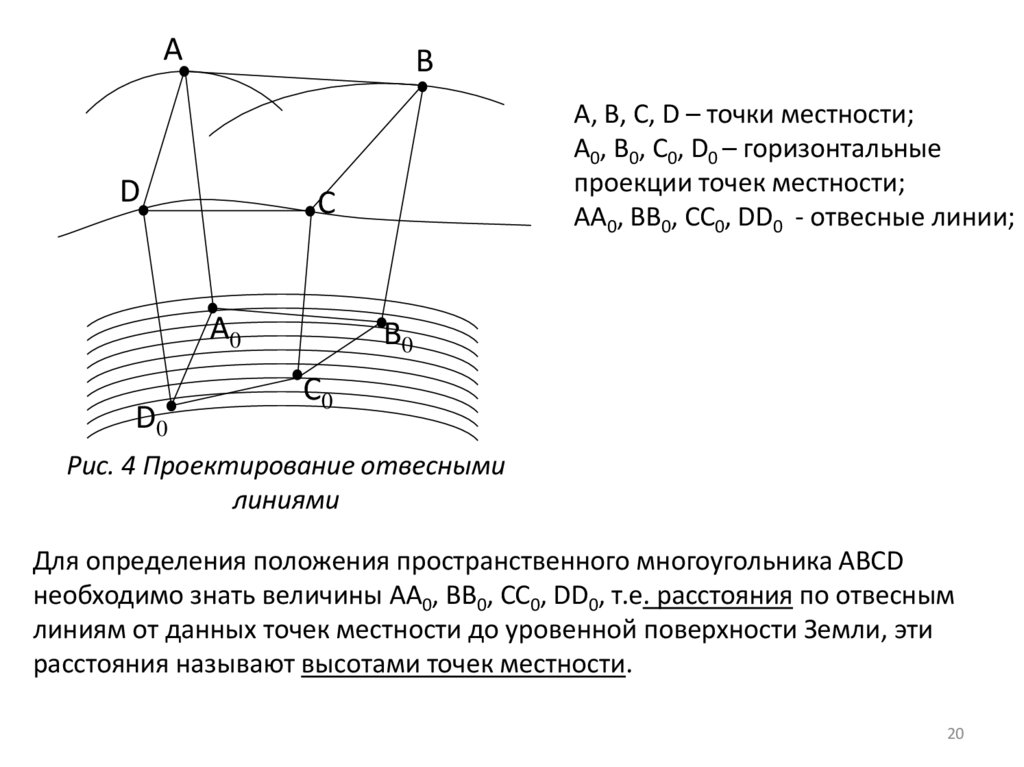





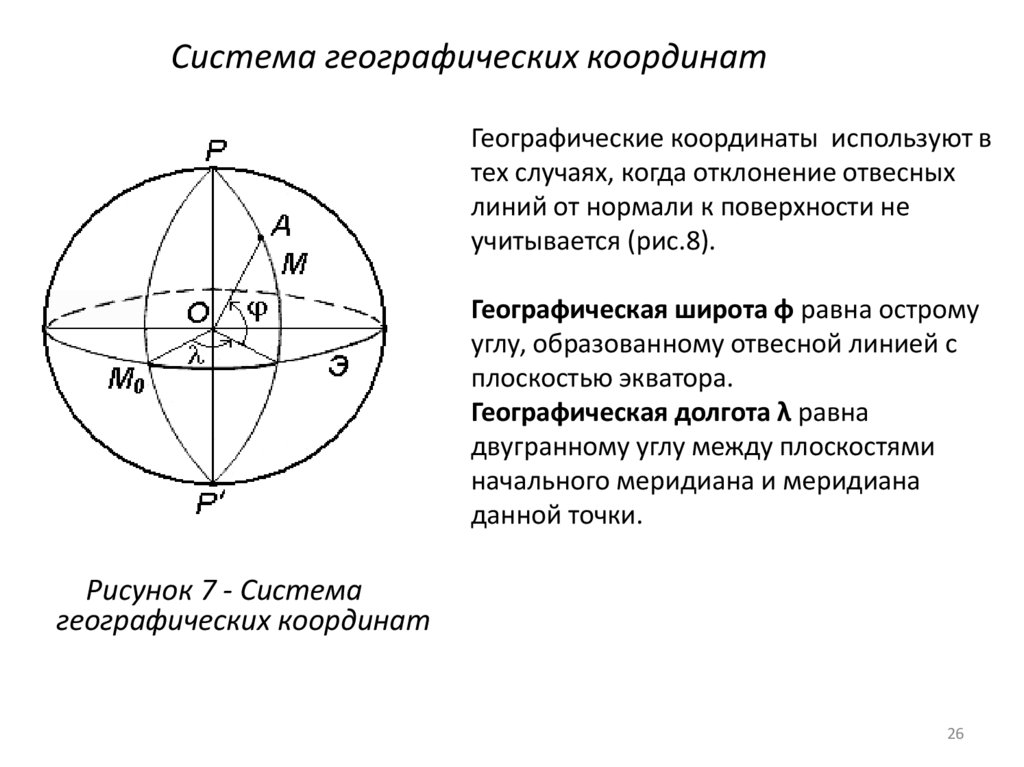

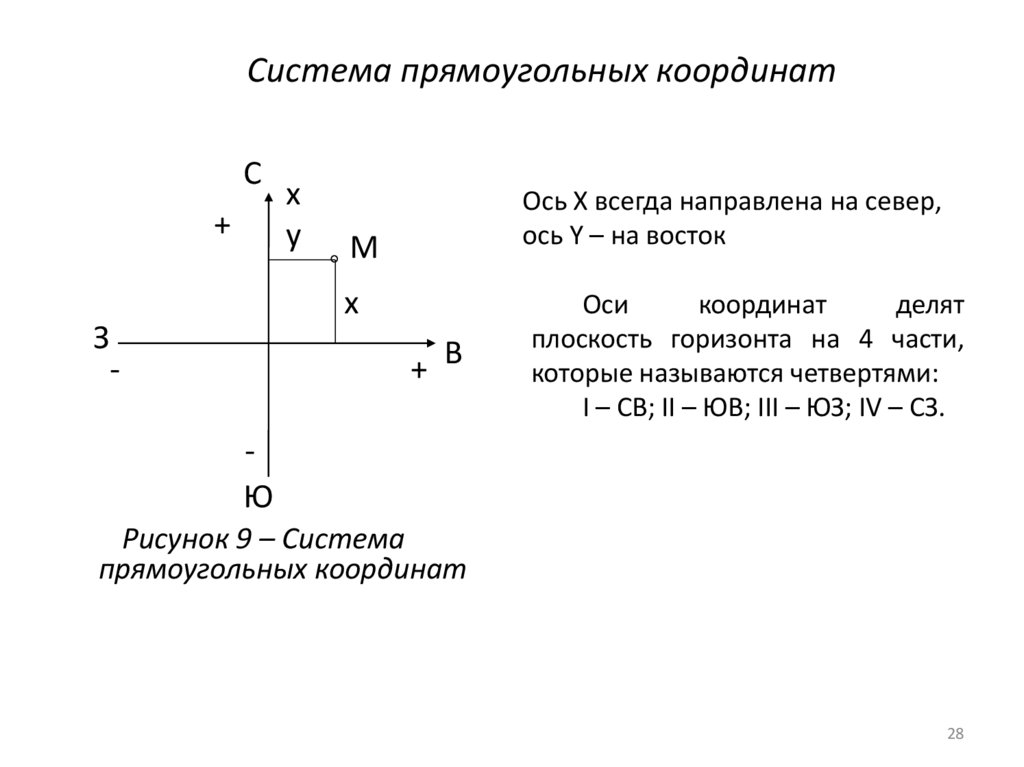


















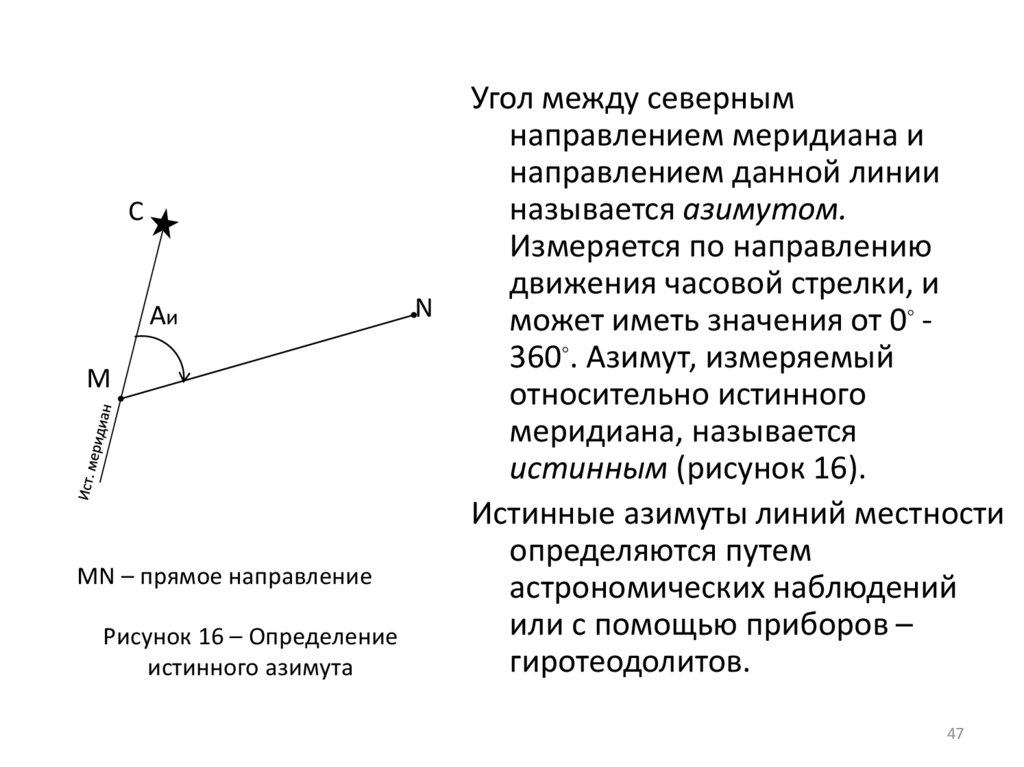







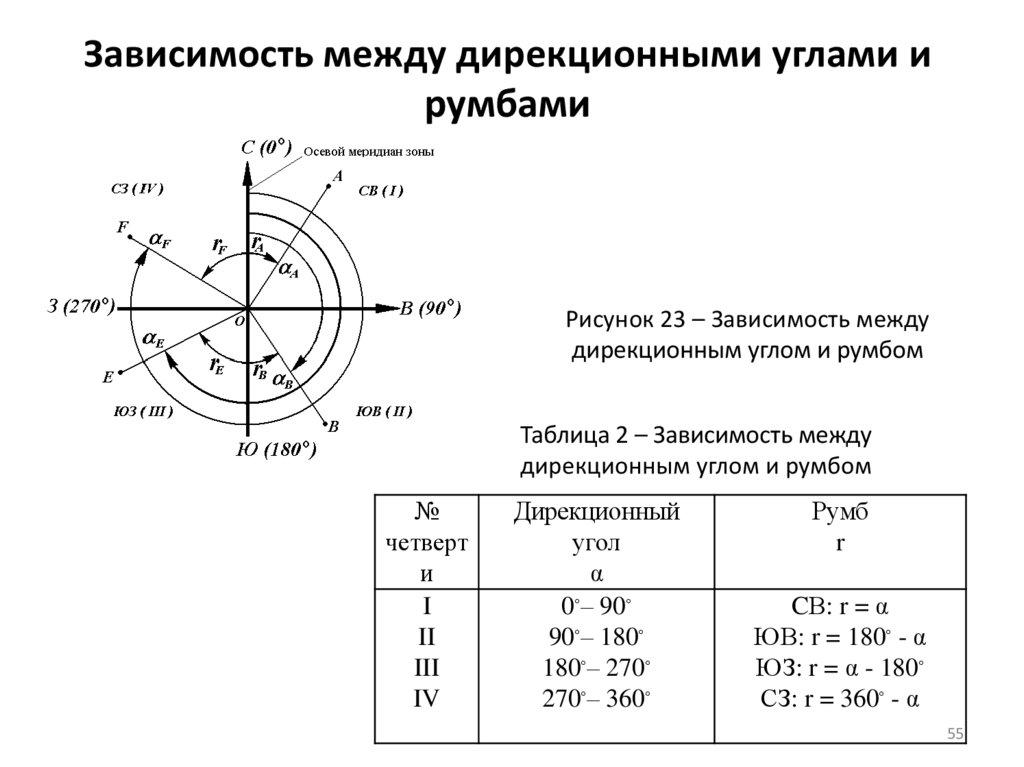

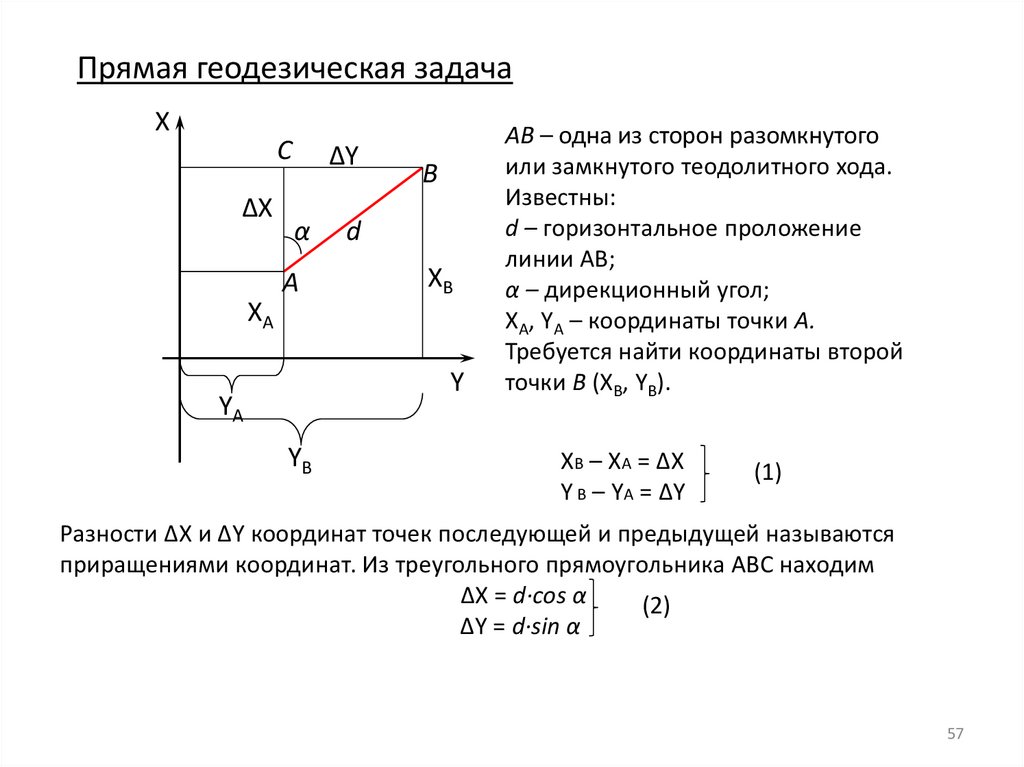
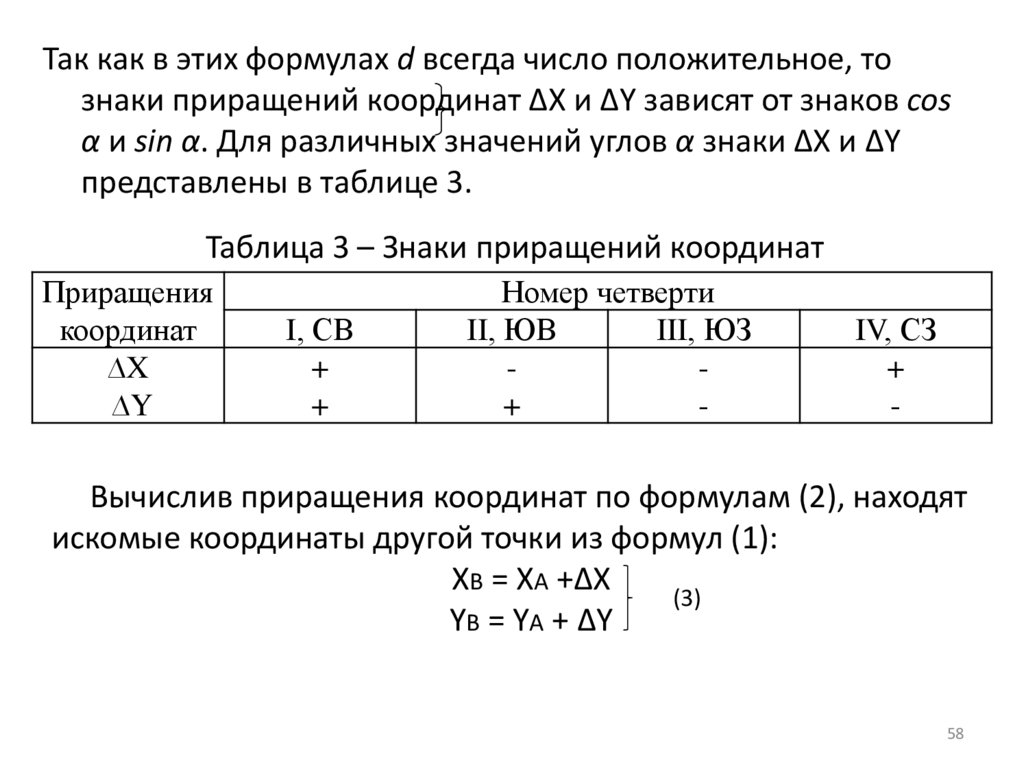


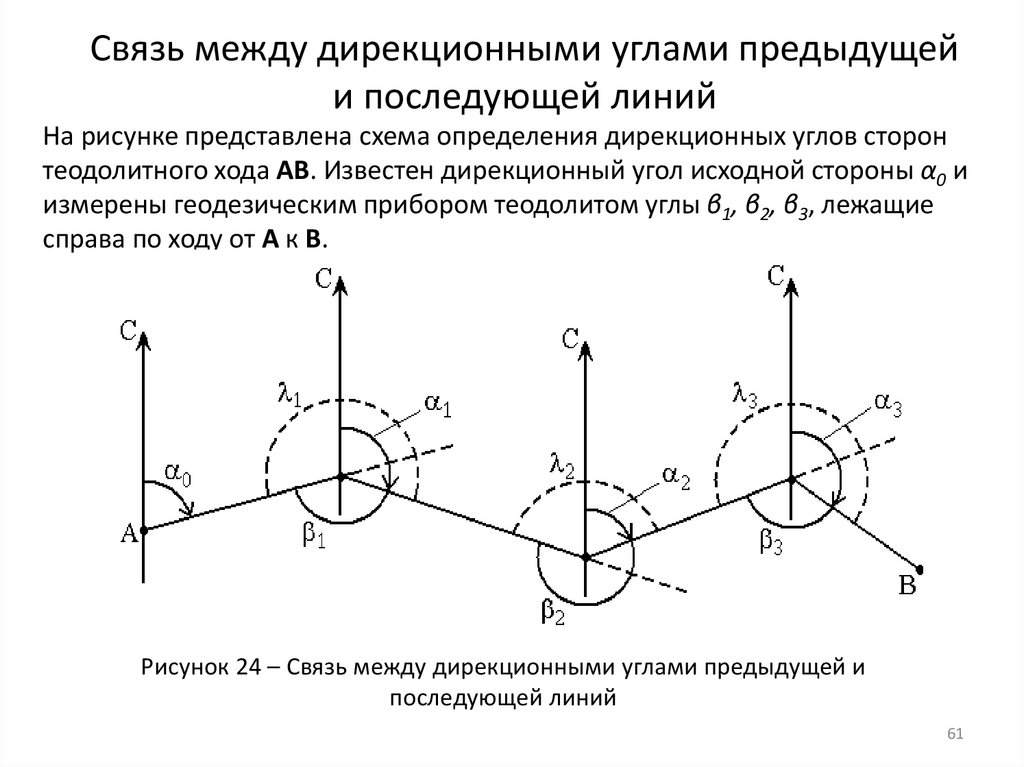









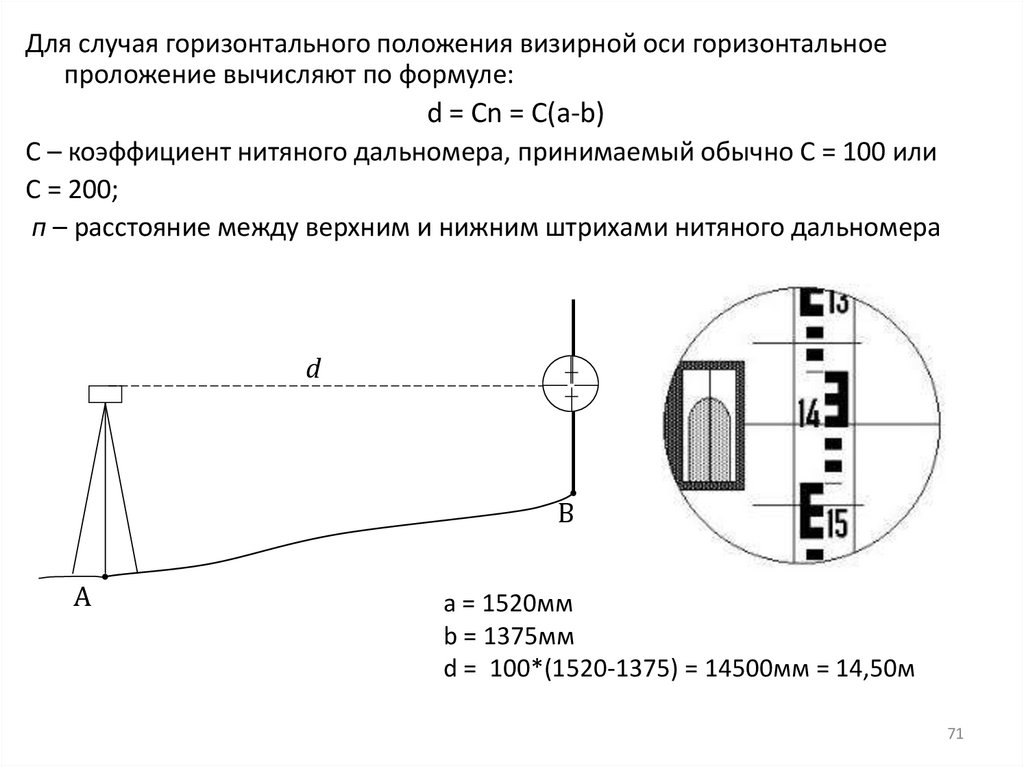
















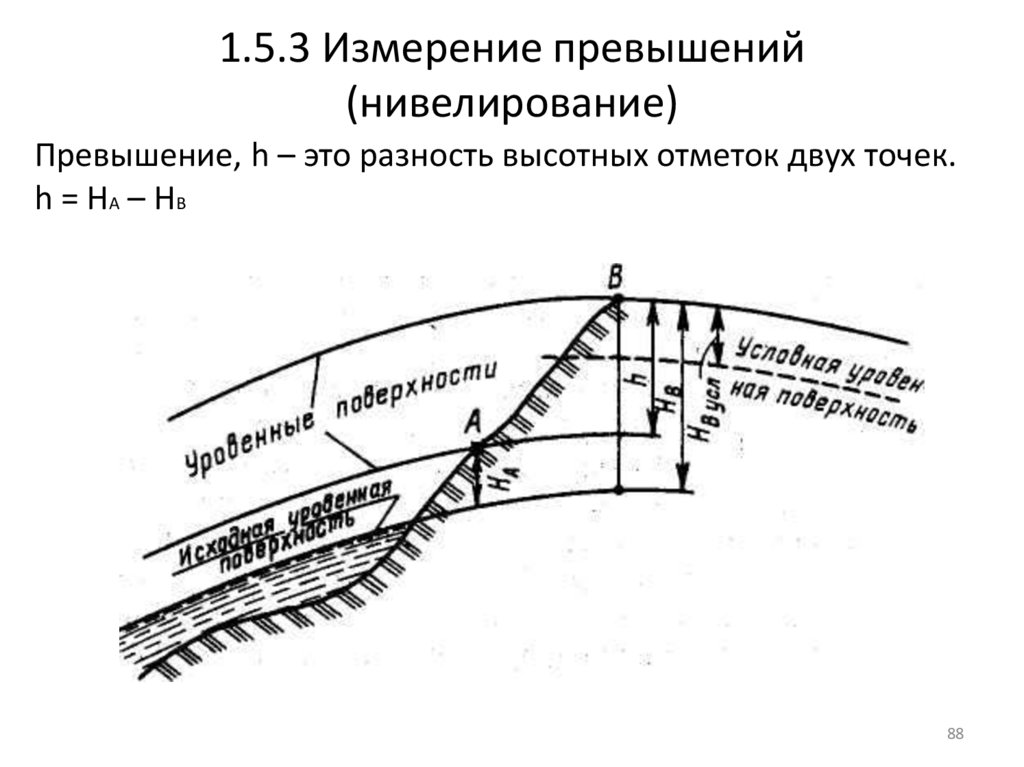


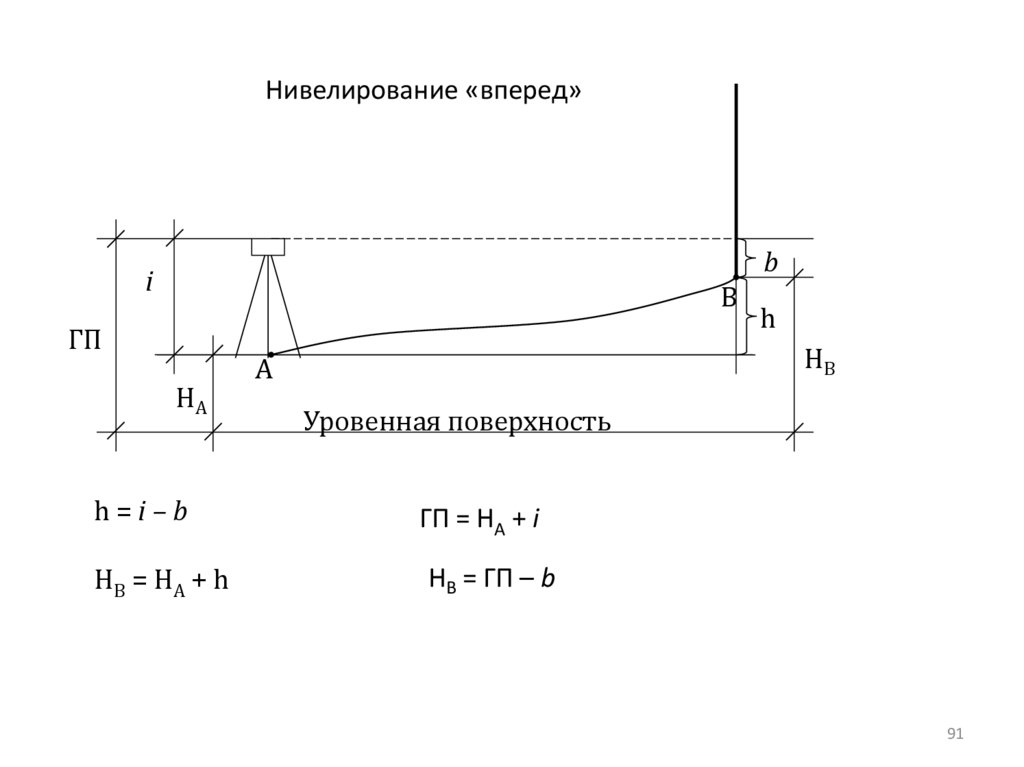




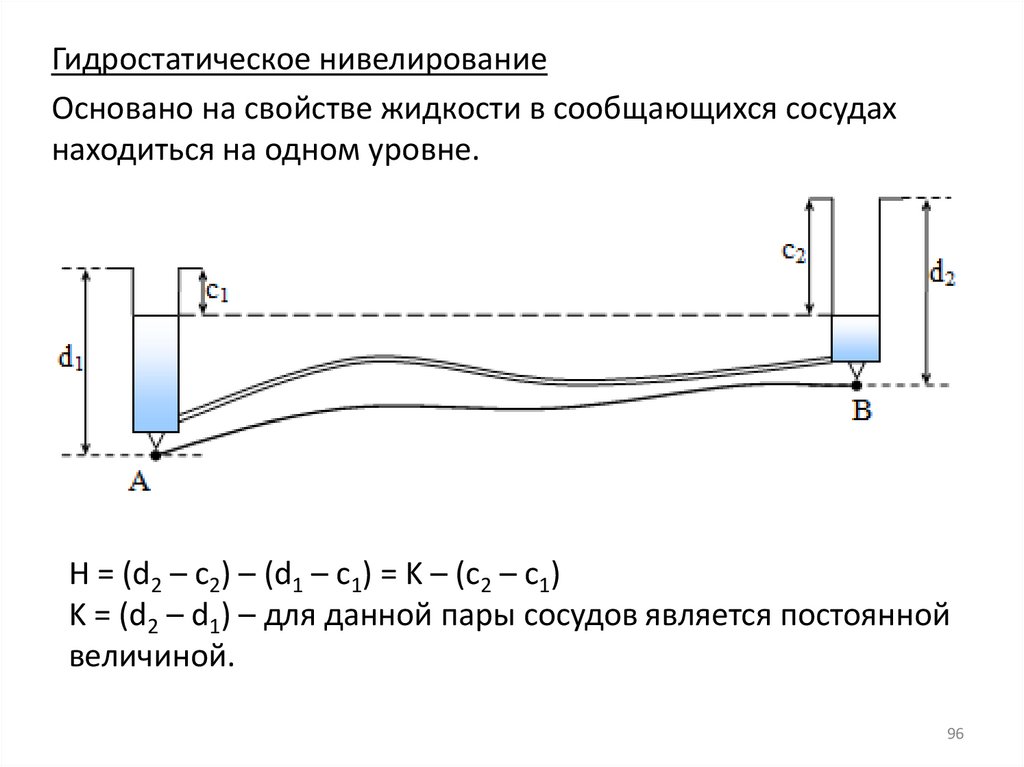








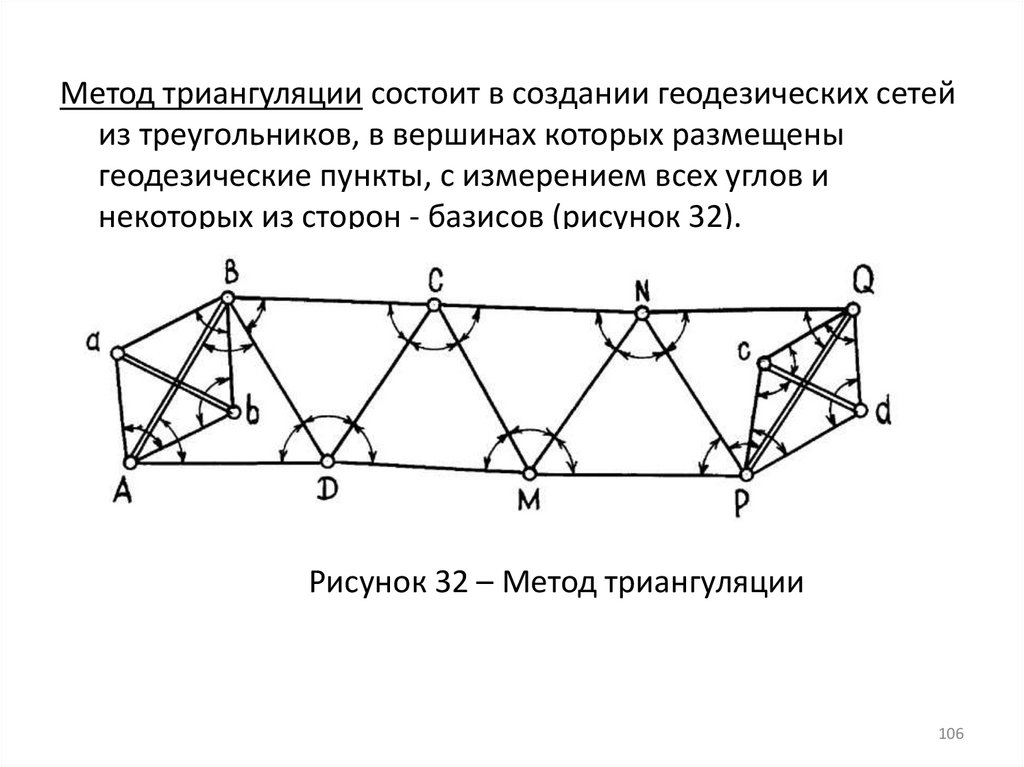

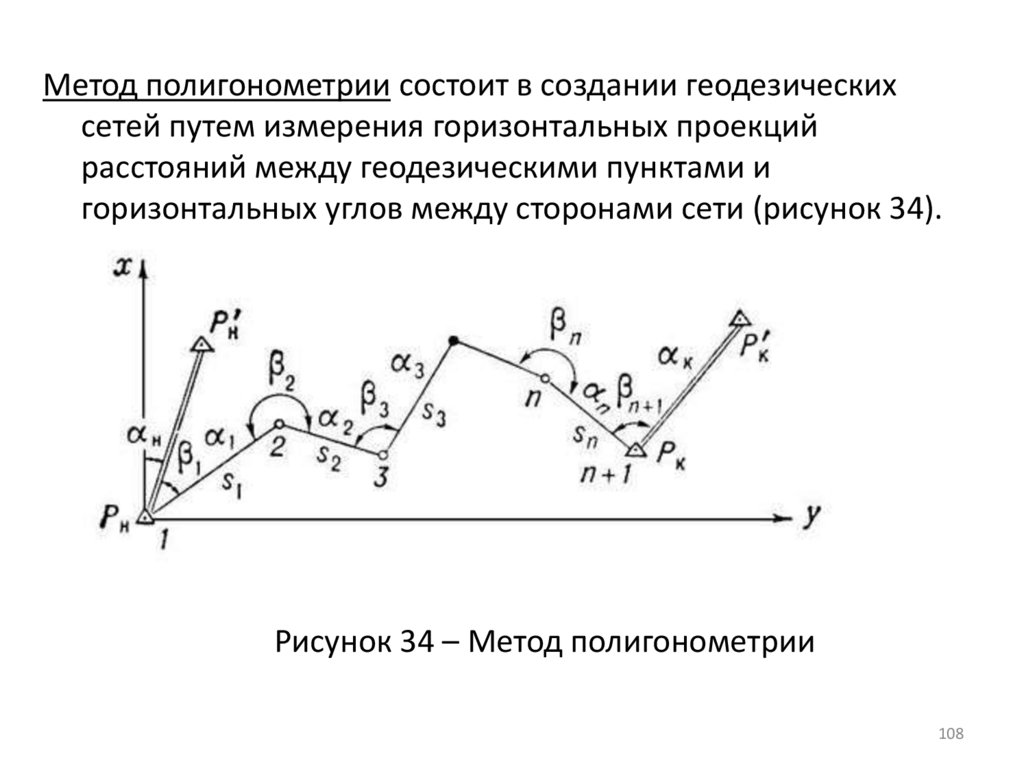

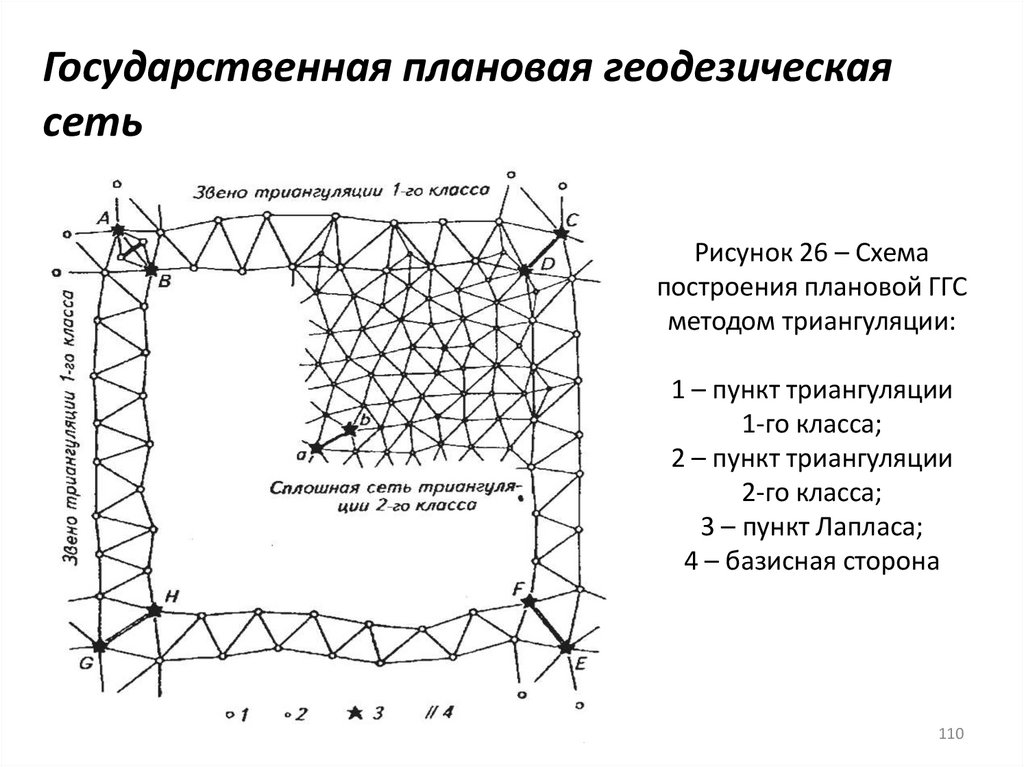
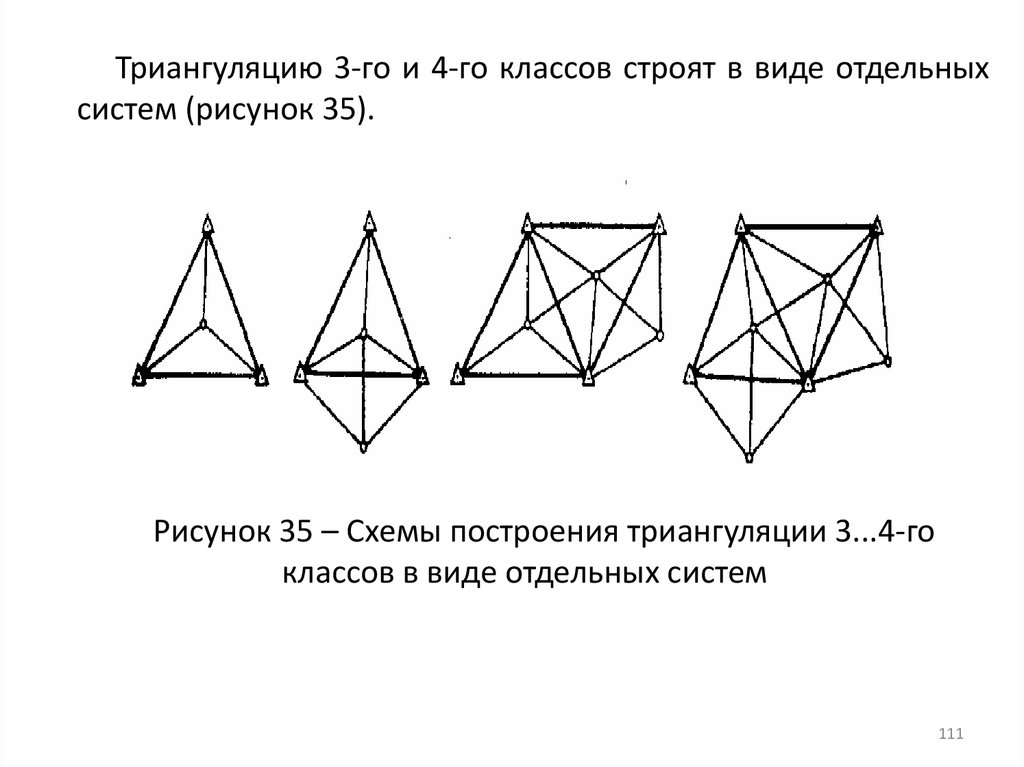
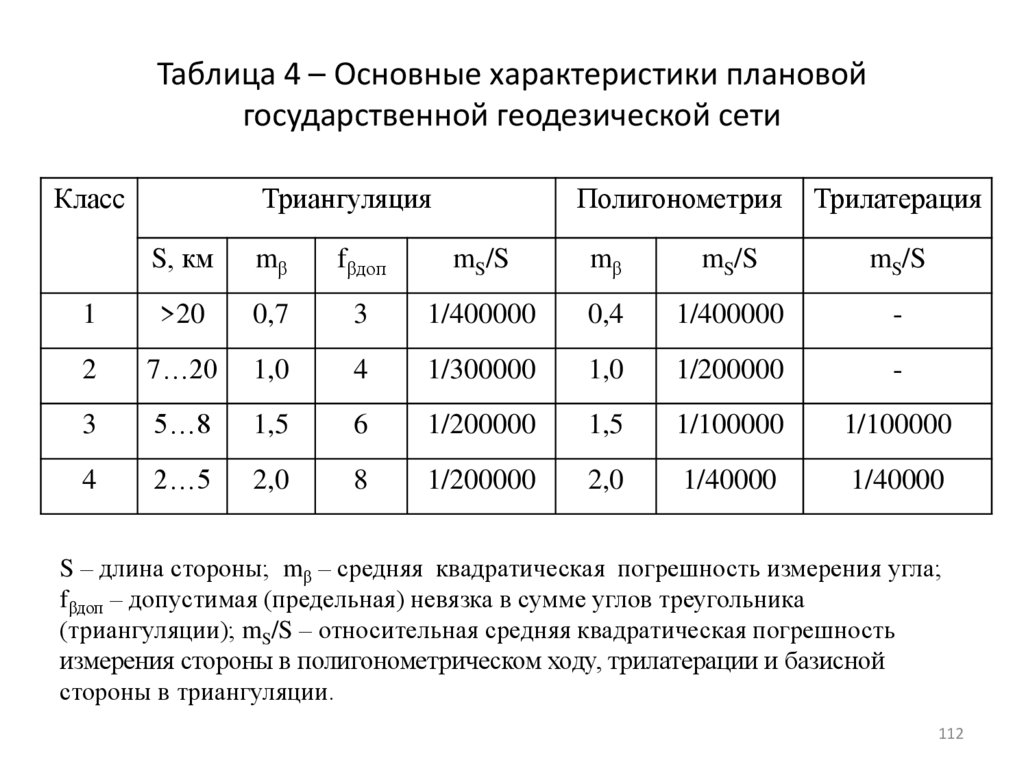







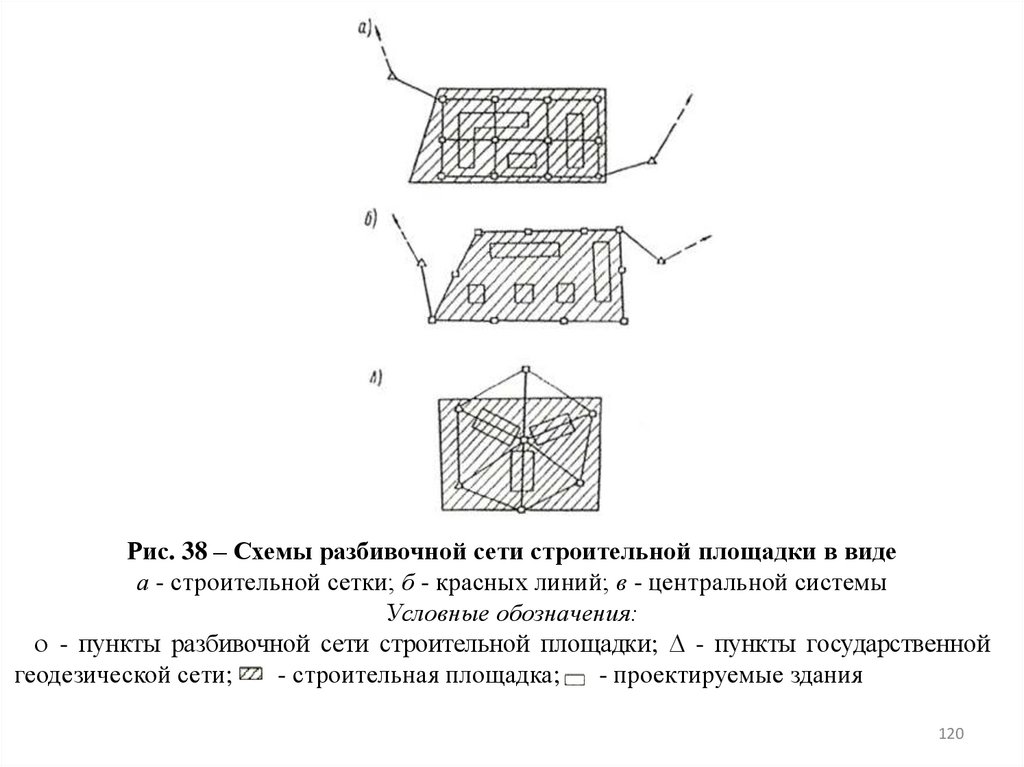









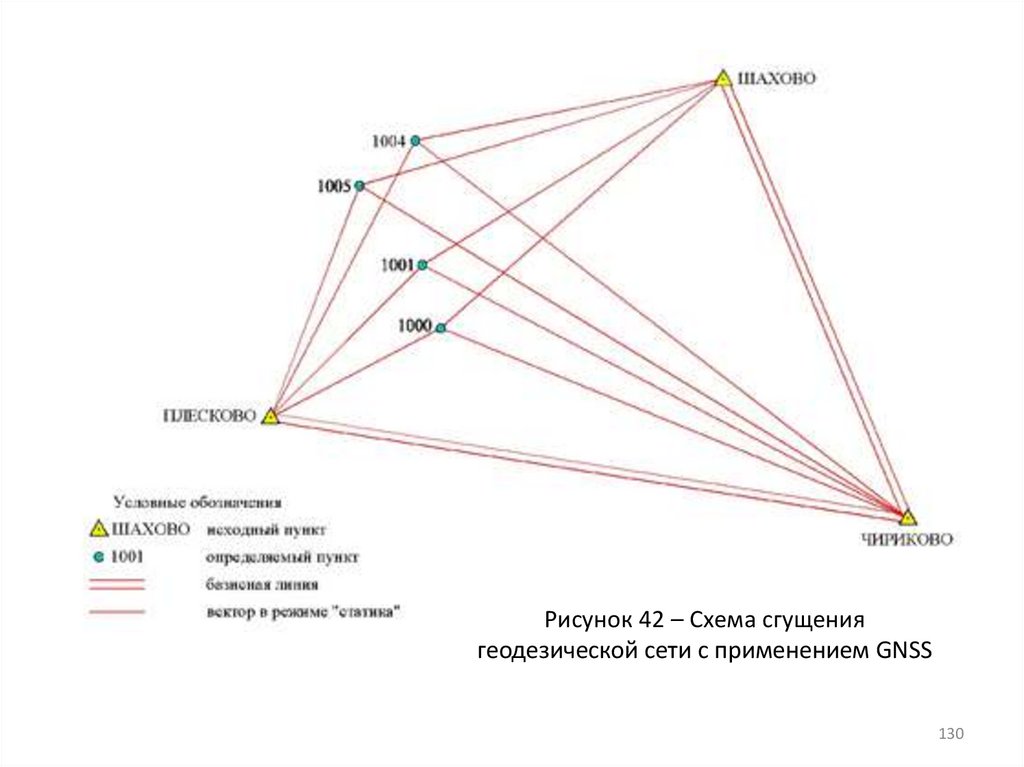






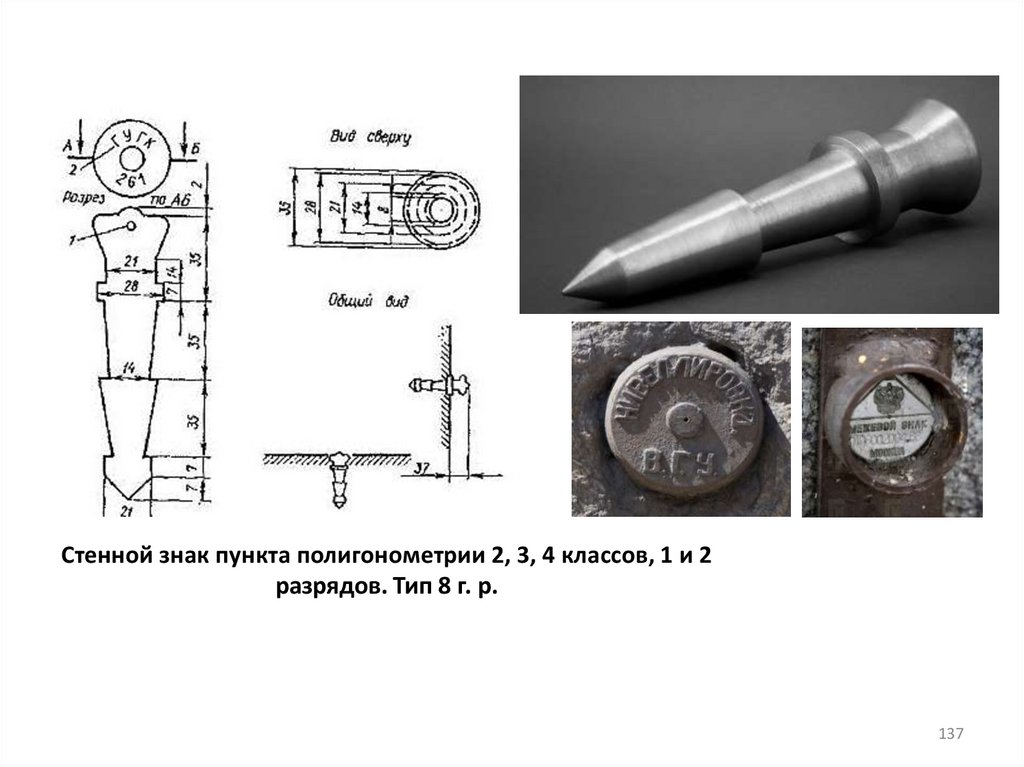


















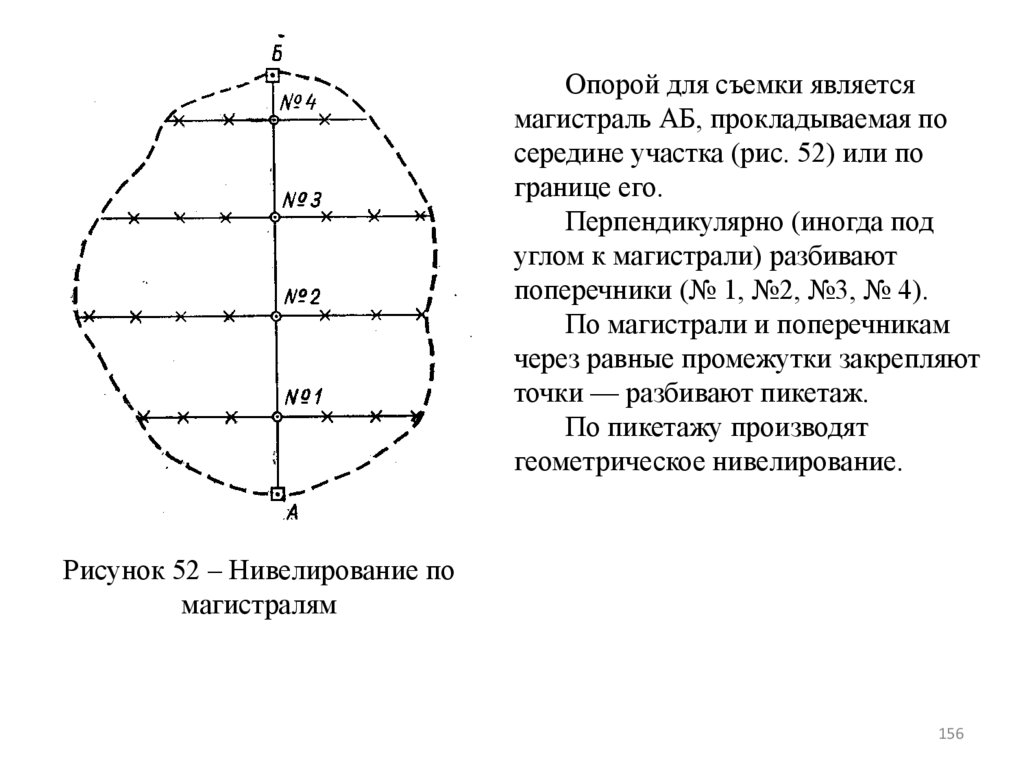












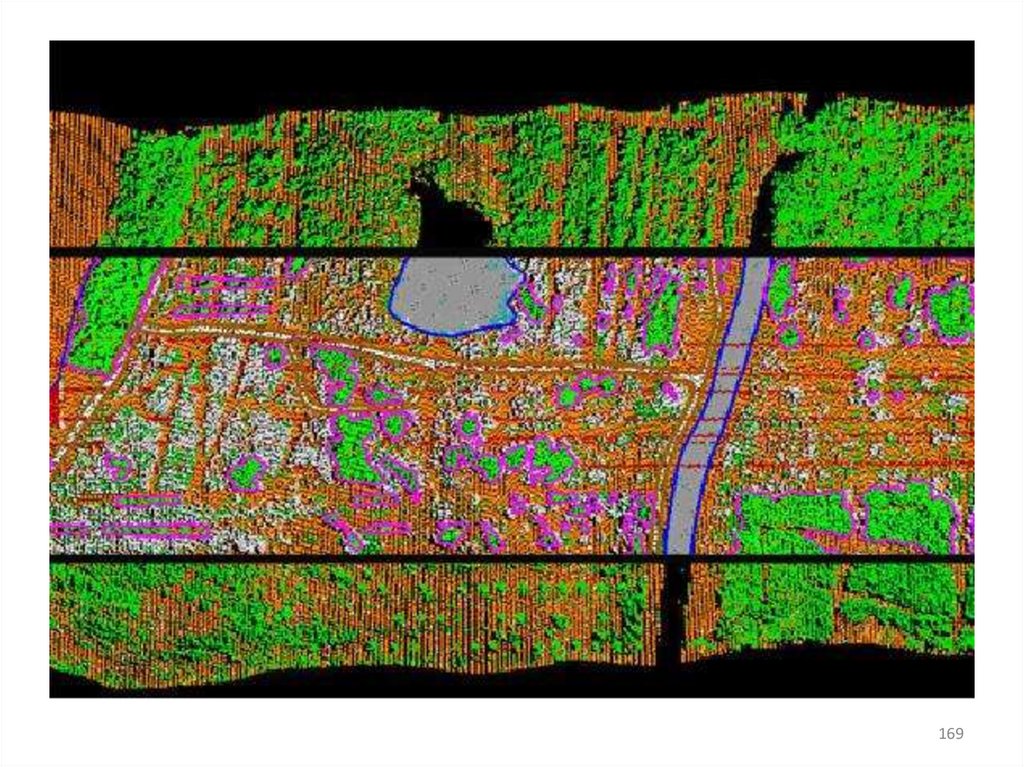


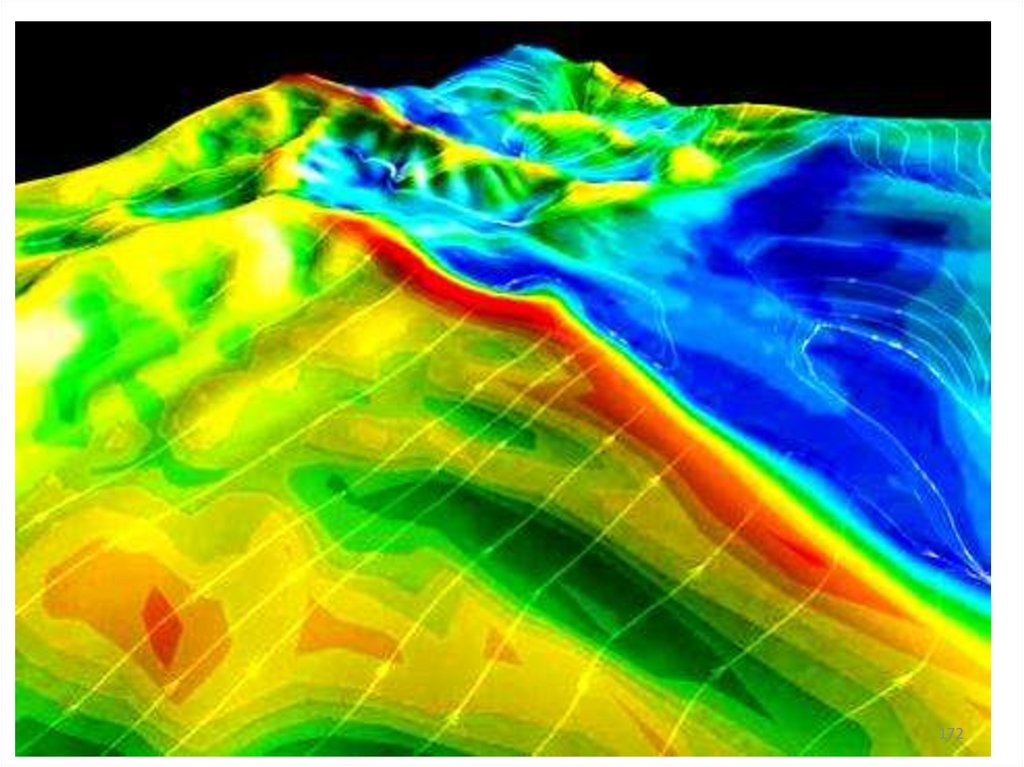













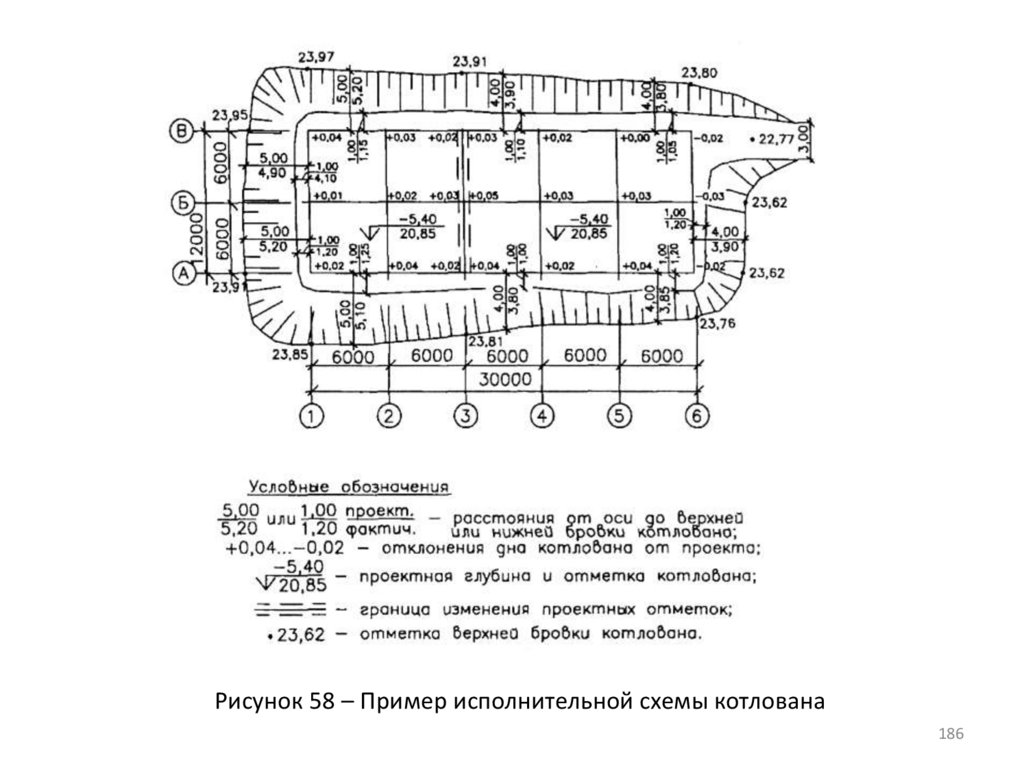
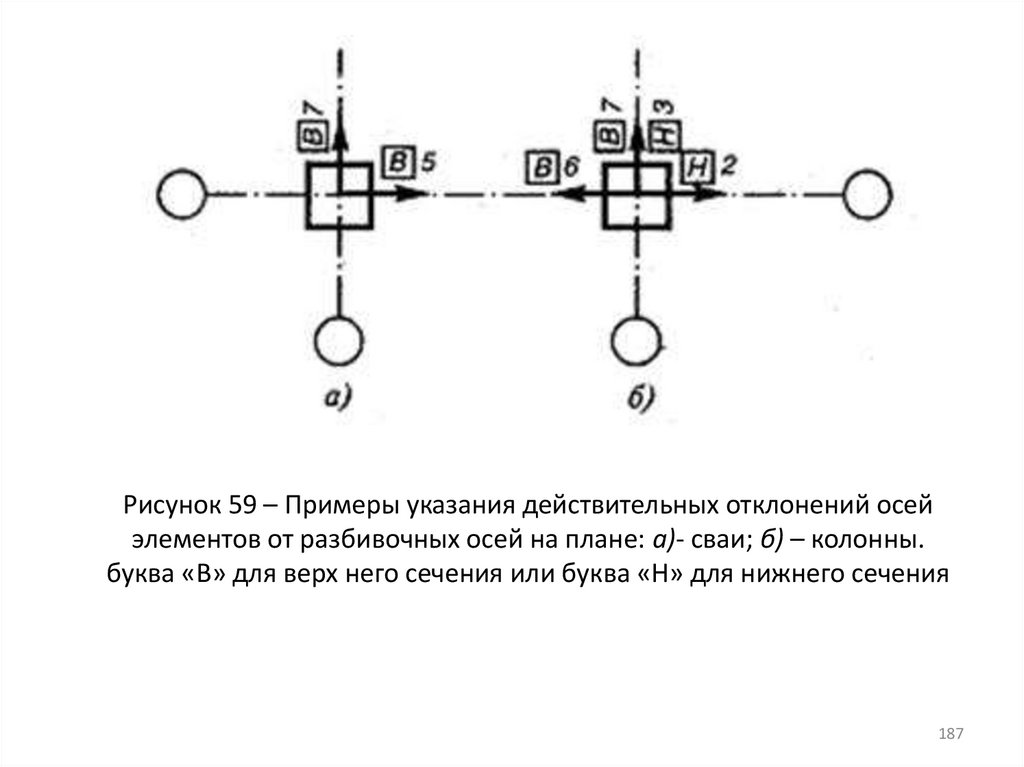







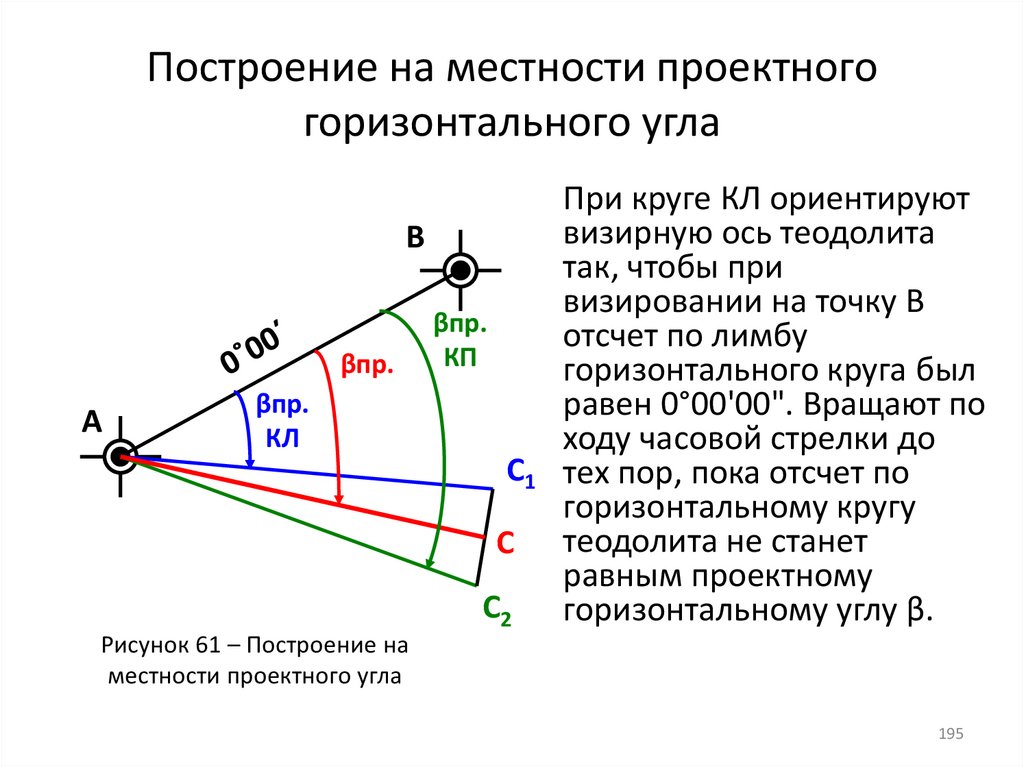





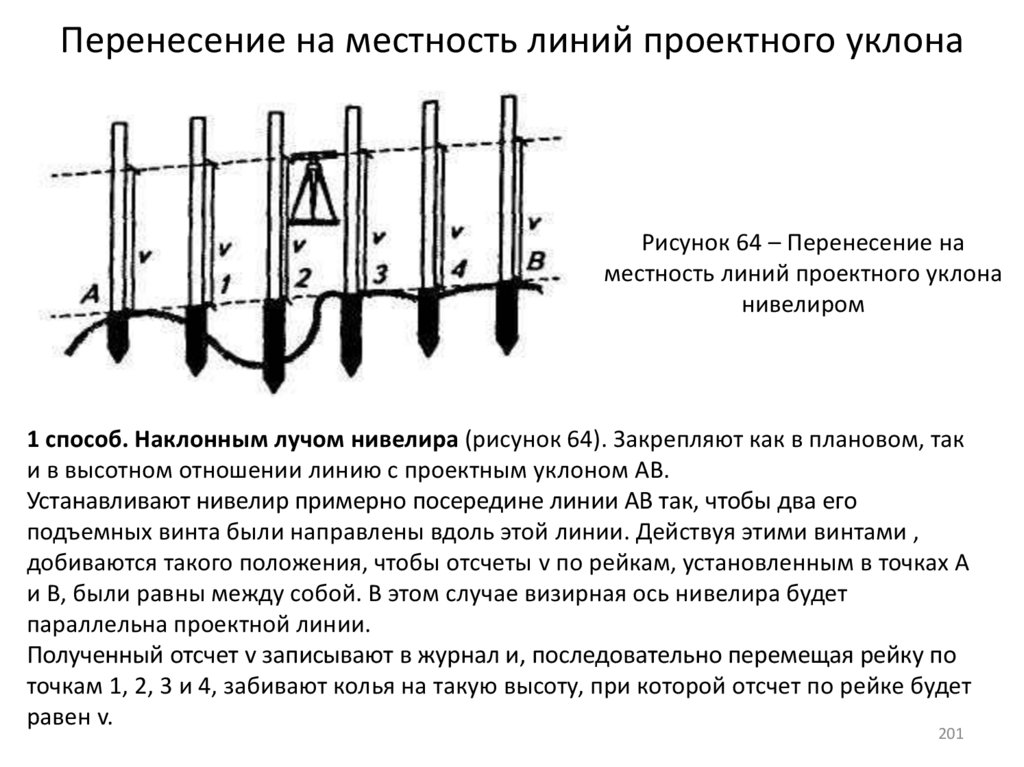


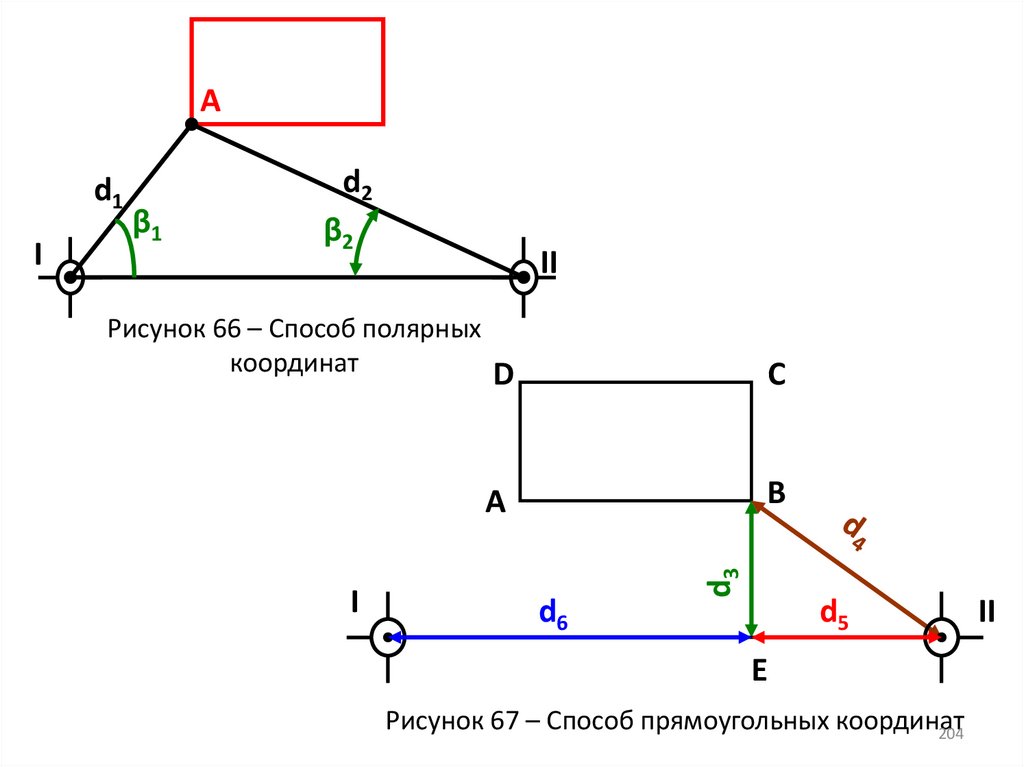
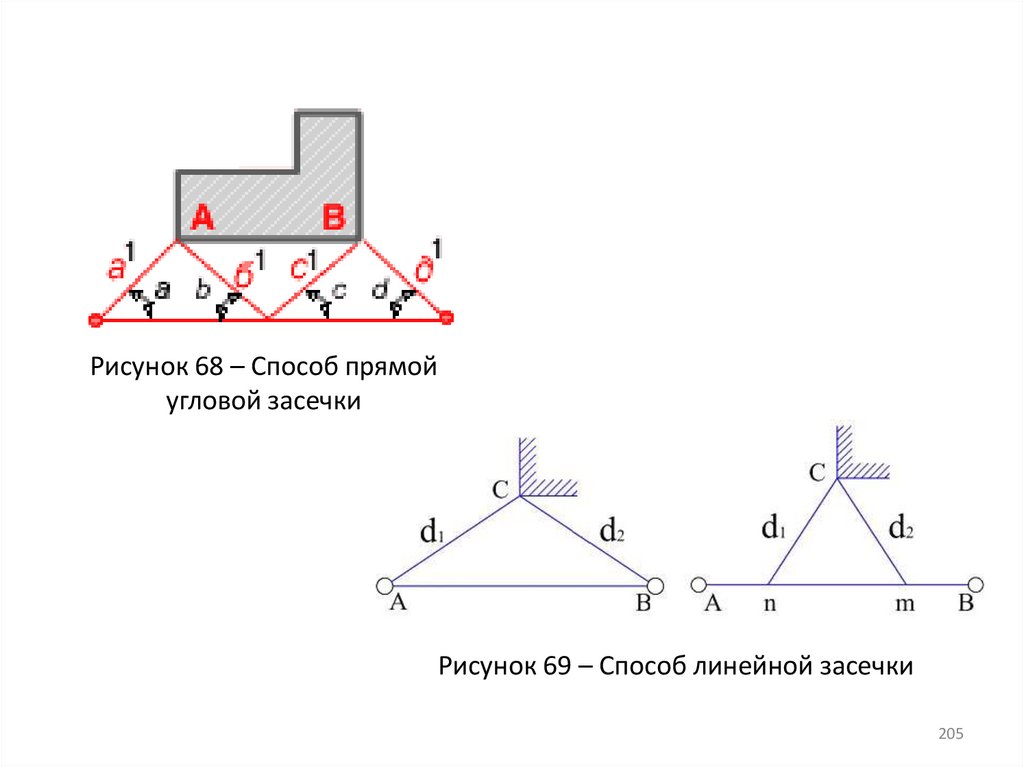

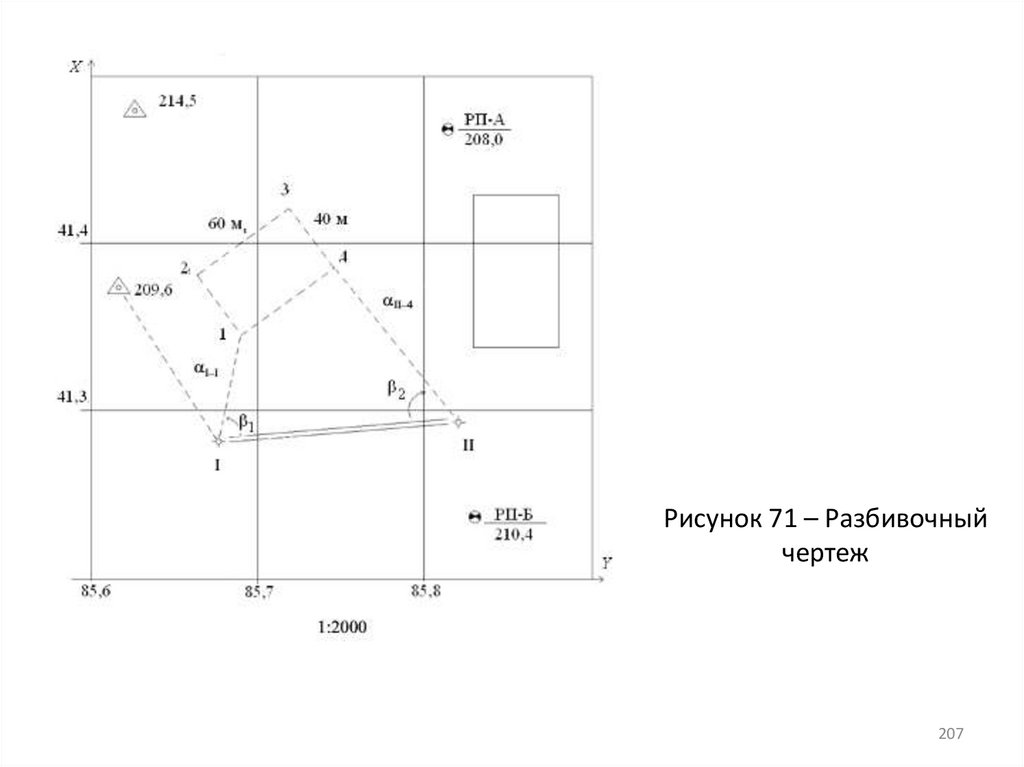




















 geography
geography








