Общие сведения по геодезии

1. Общие сведения по геодезии

2.

Геодезия – это наука об измерениях земной поверхности и ее
изображений. Геодезия (в переводе с греческого означает
«землеразделение»). В современной геодезии изучаются методы
и техника производства измерительных работ, в процессе
которых определяются фигура и размеры Земли, создаются
карты,
планы,
математические,
геометрические
и
стереоскопические модели местности, строятся вертикальные
разрезы (профили) земной поверхности.

3.

Для
проведения
любого
мероприятия,
связанного
с
использованием земли, требуется изучение земной поверхности,
ее форм рельефа, расположения объектов на ней и, прежде всего
производство специальных измерений. Поэтому в задачи геодезии
входит изучение методов:
измерений линий и углов с помощью специальных
геодезических приборов;
вычислительной обработки результатов измерений с
использованием электронно-вычислительной техники;
графических построений и оформления карт, планов и
профилей;
использование результатов измерений и графических построений
при решении задач промышленного, сельскохозяйственного,
транспортного строительства, научных исследований и др.

4.

По условиям производства работ геодезия разделяется на
наземную геодезию, где геодезические работы выполняются на
поверхности земли, на аэрофотогеодезию, предусматривающую
измерение изображений местности, полученных с воздуха, и на
космическую геодезию, где рассматриваются изображения Земли
и ее частей, полученных из космического пространства.
Специальные виды геодезических работ, проводимые под землей,
относятся к подземной геодезии – маркшейдерские работы.

5. Понятие о форме и размерах Земли

Физическая поверхность Земли представляет собой сочетание
материков и водных пространств. Материки составляют 29 %
поверхности, а моря и океаны – 71 %. Земля не является
правильным геометрическим телом. Поэтому в геодезии введено
понятие уровенной поверхности. Уровенной поверхностью
называют выпуклую поверхность, перпендикулярную к
направлению силы тяжести (отвесной линии) в каждой точке.

6.

Так как на Земле водные пространства занимают большую
площадь, то за теоретическую форму Земли принимают тело,
ограниченное поверхность океанов в спокойном состоянии,
мысленно продолженной под всеми материками.
Тело,
образованное этой поверхностью, называют геоидом.
Исследования формы Земли астрономо-геодезическими
методами показали, что Земля сплюснута у полюсов (вследствие
вращения Земли вокруг своей оси), поэтому в качестве
математической поверхности, характеризующей форму Земли,
принимают поверхность эллипсоида вращения (сфероида).

7.

Размеры эллипсоида характеризуются длинами его большой
полуоси a, малой полуоси b и сжатием , определяемым по
формуле.
a b
a

8.

Размеры Земного эллипсоида в метрах: а = 6378245,
b = 6356863, =1 / 298,3
При приближенных расчетах поверхность эллипсоида принимают
за поверхность шара с радиусом 6371,1 км, округляя это значение
до 6370 км, а в некоторых случаях до 6400 км. Для небольших
участков земной поверхности поверхность эллипсоида принимают
за плоскость.

9. Метод проекций

Для изображения земной поверхности переносят контуры или
очертания различных предметов местности и ее рельефа на сферу
или плоскость. Проектирование, главным образом, производится
ортогональным методом, т.е. отвесными линиями.

10.

Каждому контуру на физической земной поверхности
соответствует контур на уровенной поверхности. Расстояния Аа,
Bb, Cc, Dd от точек местности до уровенной поверхности
называют высотами точек. Однако сферические поверхности
неудобны для работы и поэтому прибегают к плоским
изображениям земной поверхности. Чтобы привести сферическую
поверхность вместе с изображенными объектами в плоское
изображение, прибегают к специальным картографическим
проекциям.
Чаще
всего
используется
равноугольная
картографическая проекция.

11.

Если изображаемый участок поверхности невелик, то уровенную
поверхность можно принять за горизонтальную плоскость. В
этой проекции искажаются только длины линий, а углы не
меняются, это позволяет изображать любые фигуры физической
поверхности на плоских чертежах. Проекцию линии местности
на горизонтальную плоскость называют
горизонтальным
проложением.
Задача изучения физической поверхности распадается на:
•определение положения горизонтальных проекций точек на
уровенной поверхности в определенной системе координат;
•нахождение высот точек;
•преобразование сферической уровенной поверхности в плоскую
картографическую поверхность.

12. Карта, план, профиль

Картой называют уменьшенное, построенное в картографической
проекции обобщенное изображение поверхности Земли.
Планом называется уменьшенное подобное изображение на
плоскости земной поверхности.
Профиль местности - уменьшенное изображение вертикального
разреза земной поверхности. Для усиления изображения рельефа на
профиле и большей наглядности его вертикальные отрезки (высоты,
превышения) изображают крупнее, чем горизонтальные.

13. Системы координат

Единой системой координат для точек земли является система
географических. Положение любой точки в этой системе
характеризуется широтой и долготой . Широтой называют
угол образованный отвесной линией и плоскостью экватора.
Долготой называют двугранный угол между плоскостью
начального меридиана (Гринвичский) и меридиана, проходящего
через данную точку местности.

14.

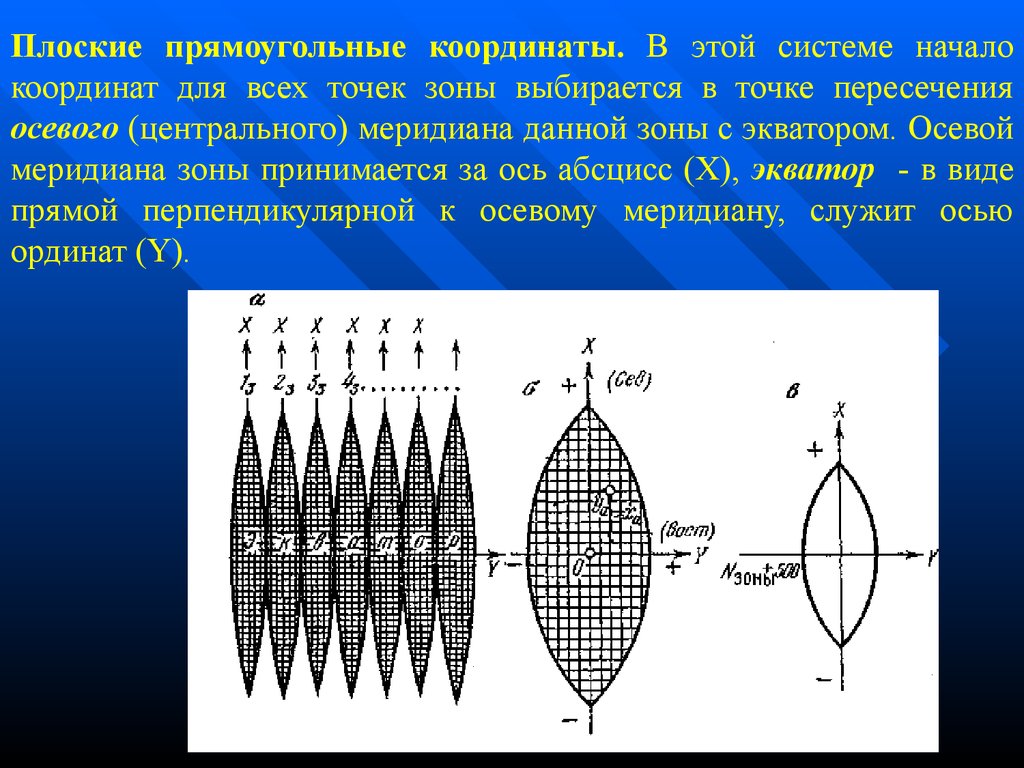
Плоские прямоугольные координаты. В этой системе начало
координат для всех точек зоны выбирается в точке пересечения
осевого (центрального) меридиана данной зоны с экватором. Осевой
меридиана зоны принимается за ось абсцисс (Х), экватор - в виде
прямой перпендикулярной к осевому меридиану, служит осью
ординат (Y).

15.

Для территории России все абсциссы положительные, чтобы не
иметь дела с различными знаками ординат, ординату точек среднего
осевого меридиана считают не за нуль, а за +500 км. Кроме того,
впереди каждой ординаты указывается еще номер зоны, в которой
расположена точка. Так как размер любой зоны вдоль оси Y всегда
меньше 1000 км, то в такой системе все ординаты положительны, а
номер зоны занимает место, соответствующее цифрам тысяч
километров. Например, запись 17 487 230 м указывает на то, что
точка находится в 17-й зоне и ее ордината Y = 487 230 – 500 000 =
-12 770 м.

16.

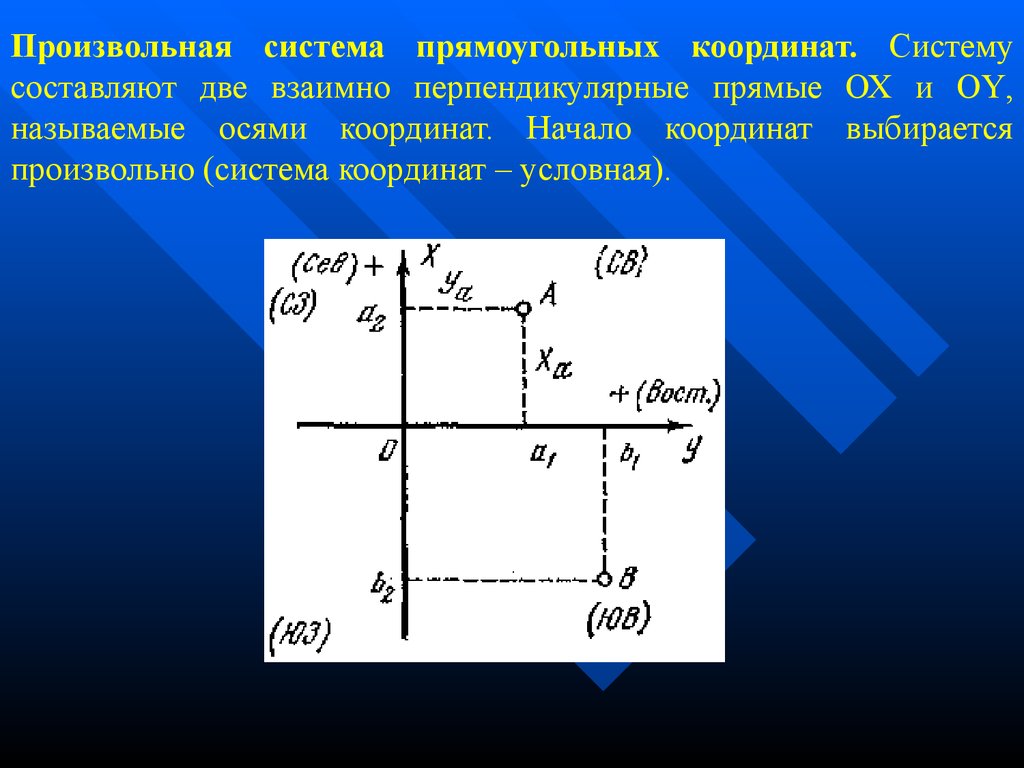
Произвольная система прямоугольных координат. Систему
составляют две взаимно перпендикулярные прямые ОХ и OY,
называемые осями координат. Начало координат выбирается
произвольно (система координат – условная).

17.

Положение любой точки характеризуется отрезками ХА и YА,
параллельными осям координат. Значения координат Х и Y
сопровождаются знаками + и - . Оси координат разделяют плоскость
чертежа на четыре части, называемые четвертями: СВ, ЮВ, СЗ, ЮЗ;
знаки координат точек, лежащих в этих четвертях показаны в
таблице.
Четверти
Координаты
I
II
III
IV
СВ
ЮВ
ЮЗ
СЗ
X
+
-
-
+
У
+
+
-
-

18. Высоты точек земной поверхности

Высотой точки называется расстояние по отвесному направлению
от нее до основной уроненной поверхности. В России она совпадает
с поверхностью воды Балтийского моря в спокойном состоянии.
Иначе их называют абсолютными высотами и обозначают через
Н, а их числовые выражения — абсолютными отметками, система
высот называется – Балтийская.
Если высоты точек определены не от основной уровенной
поверхности, а от какой-либо другой (произвольной), то такие
высоты называют условными и обозначают через H'.
Превышением, или относительной высотой точки, называется
высота ее над другой точкой земной поверхности; ее обозначают
через h.
Например, превышение точки С над точкой А будет hC = HC — HA .

19. Рельеф местности и способы его изображения

Совокупность
различных
неровностей
на
земной
поверхности
называется
рельефом. Все формы земной
поверхности подразделяют на
положительные
и
отрицательные.

20.

Рельеф местности изображают на планах и картах специальными
условными обозначениями. К ним предъявляют следующие
требования:
• должны давать представление о расположении всех форм
рельефа, о крутизне скатов;
обеспечивать определение высот отдельных точек и
превышений между ними;
• давать наглядную картину ландшафта местности.

21.

цифровой - рельеф местности на плане представляют надписями
высот характерных точек. Этот способ не дает наглядного
представления о рельефе местности.
способ штрихов - штрихи наносят параллельно скату по
принципу: чем круче скат, тем толще штрих.

22.

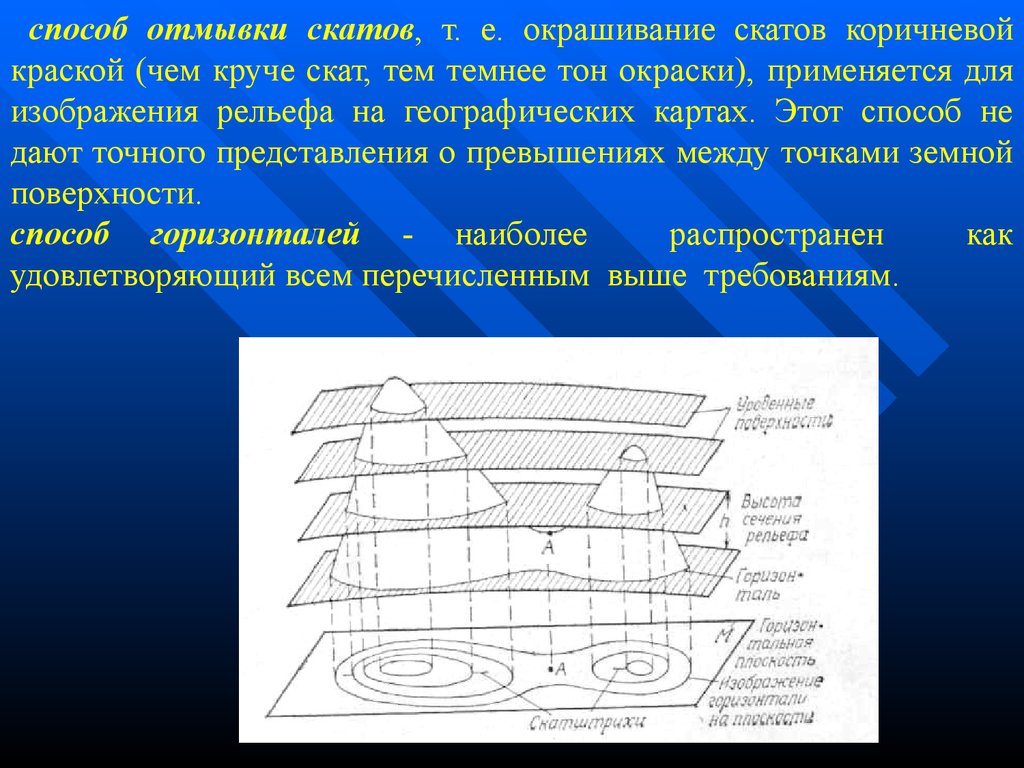
способ отмывки скатов, т. е. окрашивание скатов коричневой
краской (чем круче скат, тем темнее тон окраски), применяется для
изображения рельефа на географических картах. Этот способ не
дают точного представления о превышениях между точками земной
поверхности.
способ горизонталей - наиболее
распространен
как
удовлетворяющий всем перечисленным выше требованиям.

23.

Горизонталью называется след, от пересечения земной поверхности
плоскостями параллельными уровенной поверхности. Расстояние
между плоскостями одинаково и называется высотой сечения
рельефа.
Высоты горизонталей надписывают в разрыве горизонталей так,
чтобы нижняя часть цифр располагалась ниже по скату.
Высоты горизонталей всегда кратны высоте сечения рельефа.
Если отдельные детали рельефа, находясь между горизонталями, не
отображаются при выбранной высоте сечения рельефа, но их
положение важно отобразить, в этих местах прерывистыми линиями
проводят полугоризонтали.

24. Ориентирование линий местности

При проектных работах требуется знать расположение объектов по
отношению к странам света. В качестве основного направления при
ориентировании используется направление меридиана данной
точки. Карты и планы составляют так, что верхние их края являются
северными.
Различают меридианы: географический (истинный); магнитный;
осевой.

25.

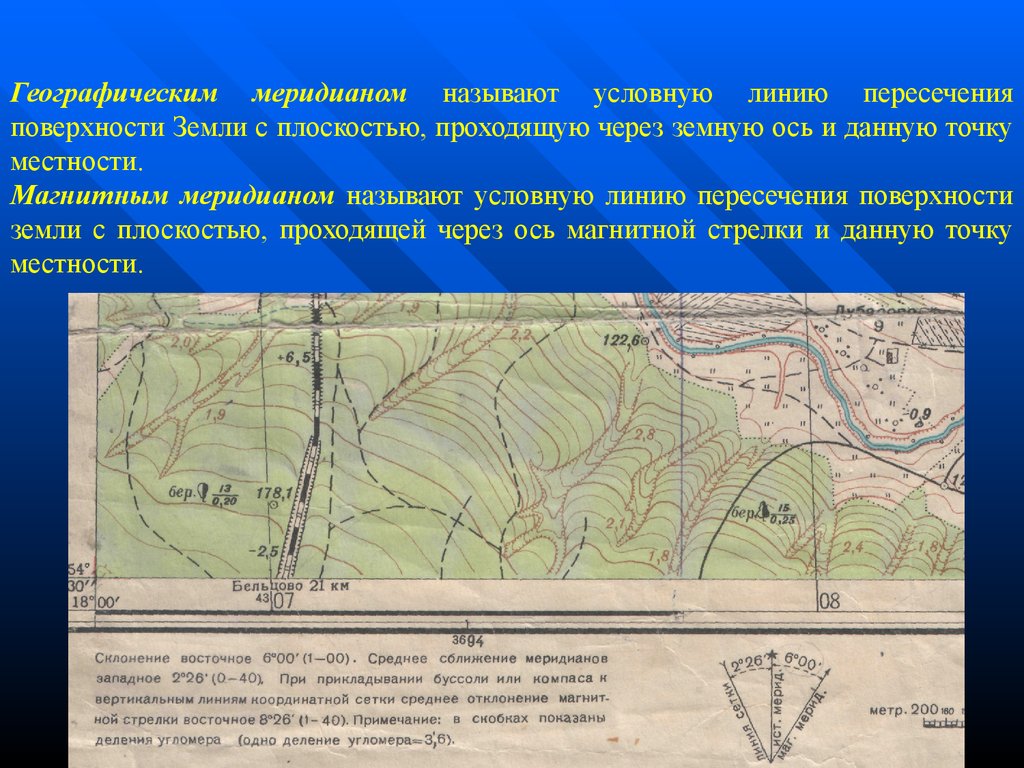
Географическим меридианом называют условную линию пересечения
поверхности Земли с плоскостью, проходящую через земную ось и данную точку
местности.
Магнитным меридианом называют условную линию пересечения поверхности
земли с плоскостью, проходящей через ось магнитной стрелки и данную точку
местности.

26.

Горизонтальный угол, образуемый направлениями географического
и магнитного меридианов, называется склонением магнитной
стрелки.
Сближение меридианов - горизонтальный угол между
направлением географического меридиана в данной точке и линией,
параллельной оси абсцисс.
Для ориентирования линий местности относительно меридиана
служат азимуты и румбы. Азимутом называется горизонтальный
угол, отсчитываемый от северного направления меридиана по ходу
часовой стрелки до направления данной линии.
Румбом называют горизонтальный угол, отсчитываемый от
ближайшего направления (северного или южного) меридиана до
направления данной линии.

27.

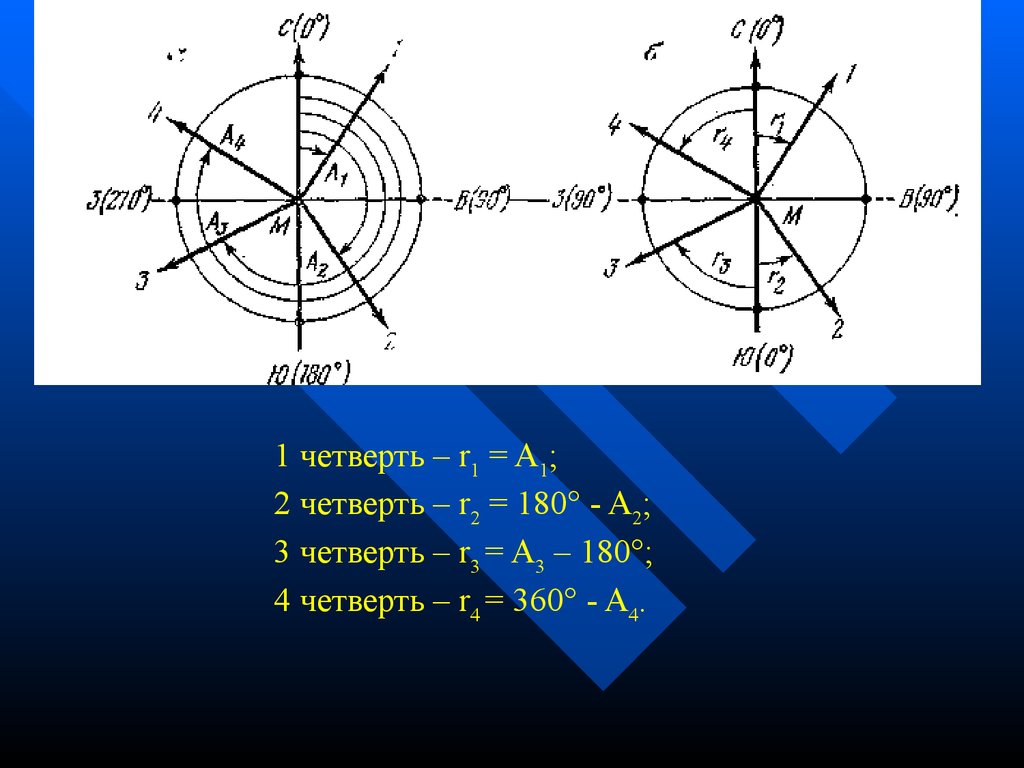
1 четверть – r1 = A1;
2 четверть – r2 = 180 - A2;
3 четверть – r3 = A3 – 180 ;
4 четверть – r4 = 360 - A4.

28.

Вычисления азимутов и румбов связаны с трудностями, так как для
прямой линии на земной поверхности в разных ее точках азимуты и
румбы изменяются из-за не параллельности меридианов. По этой
причине прямой и обратный азимуты одной и той же линии
различаются между собой не ровно на 180°.

29.

Для упрощения вычислений направлений линий пользуются
дирекционными углами.
За начальное направление принимается осевой меридиан 6-ти или
3-х градусной зоны. Все направления в пределах зоны измеряются
от осевого меридиана или линии параллельной ему.
Дирекционным углом ( ) называют горизонтальный угол,
отсчитываемый от северного направления осевого меридиана или
линии параллельной ему, по ходу часовой стрелки до направления
данной линии.

30. Элементы измерений на местности

Чтобы нанести контур на карту, план или профиль, выбирают
характерные точки, например вершины углов ломаных контуров,
определяют их взаимное положение.
Взаимное положение точек местности определяют путем измерений
линий (расстояний) между точками и углов между направлениями
линий, соединяющих точки. Для измерения линий применяют
различные линейные мерные приборы, для измерения углов —
угломерные приборы.

31.

Взаимное положение точек А и В на местности определяют
измерением расстояния АВ (рис. а), которое затем проектируют
нормалями на поверхность эллипсоида. В проекции получается
кривая А1В1, используемая для составления карты.
При выполнении геодезических работ на небольшой территории,
когда не учитывают кривизну Земли, линию местности АВ
проектируют ортогонально на горизонтальную плоскость, (рис. б).
В проекции получается прямая аb, называемая горизонтальным
проложением
линии
АВ
местности.
Таким
образом,
горизонтальным
проложением
называют
проекцию
(ортогональную) линии местности на горизонтальную плоскость.
Его используют для составления плана.

32.

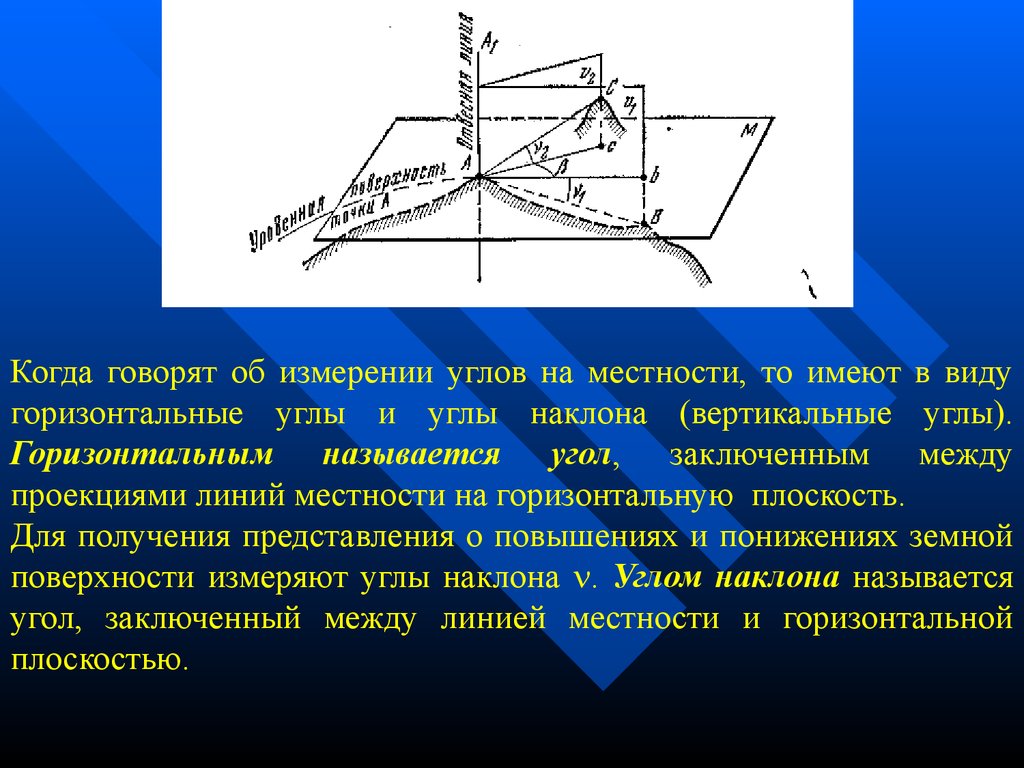
Когда говорят об измерении углов на местности, то имеют в виду
горизонтальные углы и углы наклона (вертикальные углы).
Горизонтальным называется угол, заключенным между
проекциями линий местности на горизонтальную плоскость.
Для получения представления о повышениях и понижениях земной
поверхности измеряют углы наклона . Углом наклона называется
угол, заключенный между линией местности и горизонтальной
плоскостью.

33.

Измерив длину линии на местности АВ = Д и угол наклона ,
горизонтальное проложение аb = d вычисляют по формуле
d D cos
Вместо вычисления по этой формуле можно в результат измерения
D ввести поправку ΔD за наклон линии к горизонту
ΔD = 2D sin2 (ν/2)
Поправку ΔD всегда вычитают из результата измерения D
d = D —ΔD

34. Прямая геодезическая задача

Состоит в том, что по координатам одного конца А (хА и уА) линии
АВ, по дирекционному углу этой линии αАВ и ее горизонтальному
проложению dАВ вычисляют координаты другого конца В этой
линии (хВ и уВ). То есть известно: хА, уА, αАВ, dАВ; вычислить хВ и уВ.
х В х А х АВ
у В у А у АВ
х АВ d АВ cos АВ
у АВ d AB sin AB
x B x A d AB cos AB
y B y A d AB sin AB

35. Обратная геодезическая задача

состоит в том, что по координатам концов линии АВ вычисляют
дирекционный угол и горизонтальное проложение этой линии. То
есть известно: хА, уА, хВ, уВ; надо вычислить αАВ, dАВ .
x AB x B x A
y AB y B y A
d AB
x AB
x xA
B
cos AB cos AB
d AB
y AB
y yA
B
sin AB
sin AB
tg AB
d AB
sin AB
yB y A
xB x A
xB x A
yB y A
d AB
2
yB y A
cos AB
xB x A
d AB
2

36. Передача дирекционного угла на линию

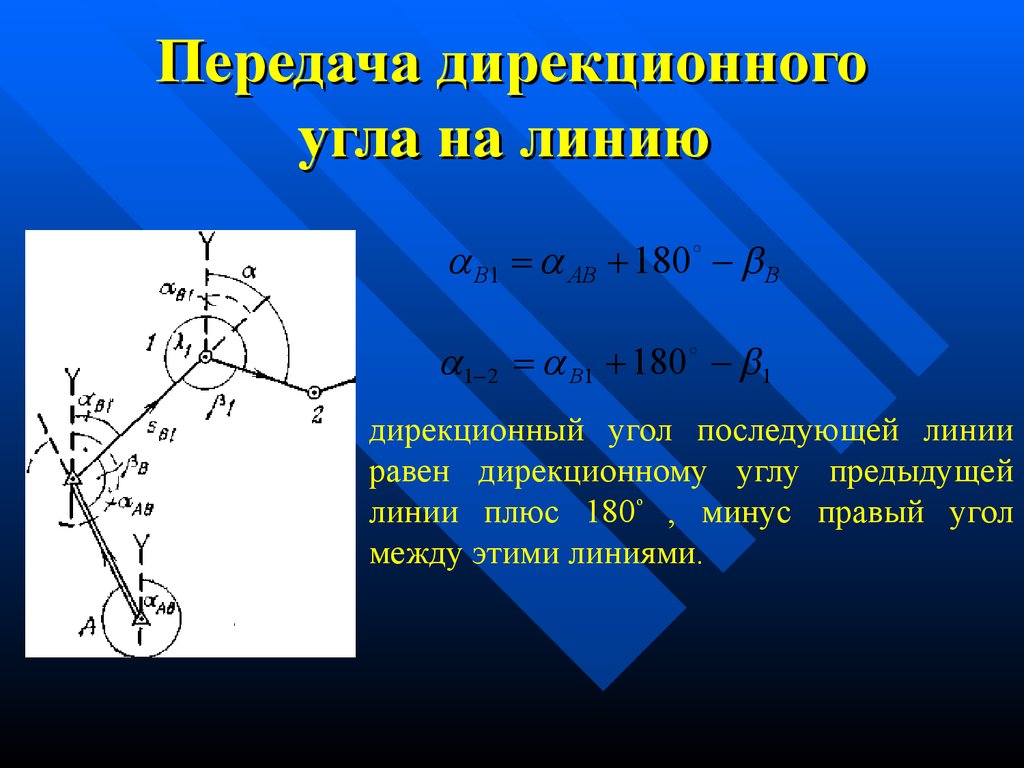
В1 АВ 180 В
1 2 В1 180 1
дирекционный угол последующей линии
равен дирекционному углу предыдущей
линии плюс 180º , минус правый угол
между этими линиями.

37.

Если на местности измерены левые углы, например вместо правого β 1 левый γ1,
то, подставив
1 360 1
1 2 В1 180 360 1
1 2 В1 2 180
т. е. дирекционный угол последующей линии равен дирекционному
углу предыдущей линии плюс левый угол между этими линиями,
минус 180º.
Так можно последовательно вычислить дирекционные углы линий,
имея измеренные углы между ними.