Similar presentations:
Химическая термодинамика. Экзаменационные вопросы
1.
Экзаменационные вопросы4. Химическая термодинамика
1. Основные понятия. Термодинамическая система, параметры и функции состояния.
Термодинамический процесс. Обратимый (равновесный) и необратимый (неравновесный)
процессы.
2. Первое начало термодинамики. Внутренняя энергия и энтальпия.
3. Тепловой эффект химической реакции. Закон Гесса и его следствия. Стандартная (молярная)
энтальпия образования вещества. Термохимические расчеты.
4. Температурная зависимость энтальпии (теплового эффекта).
5. Энтропия. Второе начало термодинамики. Связь энтропии и термодинамической вероятности
системы. Уравнение Больцмана. Формулировка второго и третьего начала термодинамики.
Факторы, влияющие на величину энтропии.
6. Энергия Гиббса. Направление протекания химического процесса. Термодинамическое условие
равновесия. Стандартная энергия Гиббса (образования) вещества.
7. Температурная зависимость величины энергии Гиббса. Энтальпийный и энтропийный
факторы. Оценка термодинамической возможности протекания химической реакции.
8. Энергия Гиббса в нестандартных условиях. Концентрационная зависимость энергии Гиббса.
Активность и фугитивность.
2.
4. Термодинамика (т/д)В своём развитии пришла к основным обобщениям – началам (законам) т/д.
Всё остальное содержание т/д – есть следствие из них. Её отличают
логичность,
последовательность,
согласованность
количественных
результатов, высокая степень формализма. Законы т/д выведены для
абстрактных систем и столь общи, что широко используются в физике,
биологии, геологии, астрономии, математике, химии.
т/д изучает
• превращения (переходы) энергии из одной формы в другую, от
одной части системы к другой
•энергетические эффекты, сопровождающие физические и
химические процессы
•возможность, направления и предел самопроизвольного
протекания процессов.
Химическая термодинамика - термодинамика хим. процессов.
Описывает статистически значимые процессы (большое число
частиц или случаев)
3.
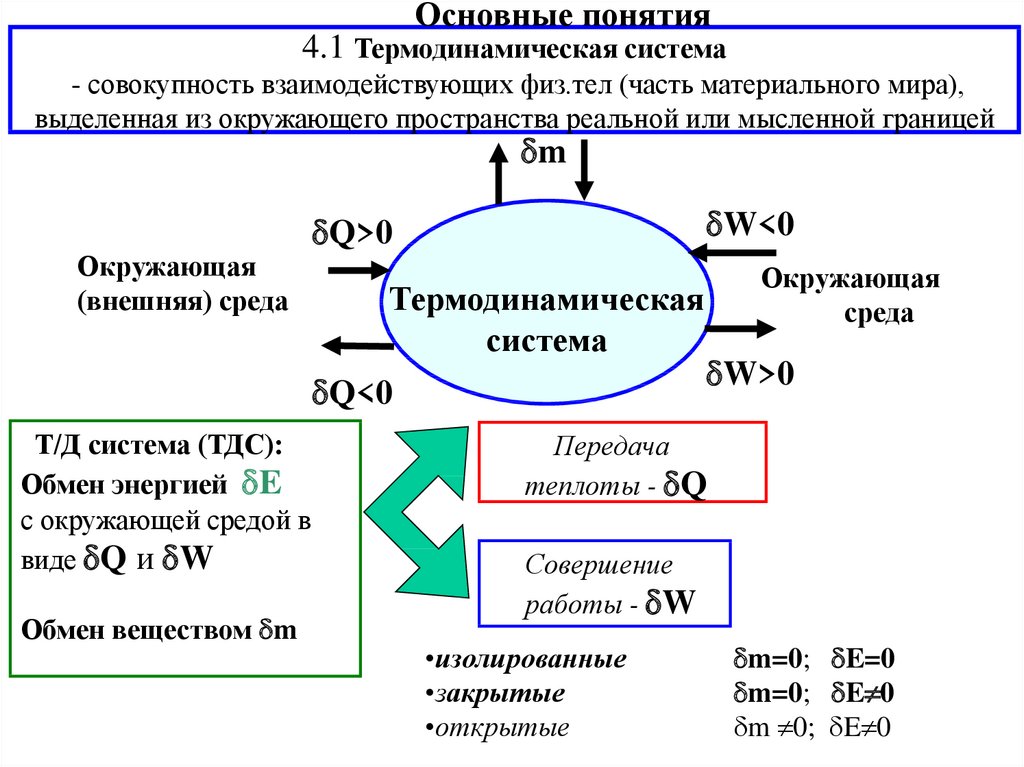
Основные понятия4.1 Термодинамическая система
- совокупность взаимодействующих физ.тел (часть материального мира),
выделенная из окружающего пространства реальной или мысленной границей
m
Окружающая
(внешняя) среда
W<0
Q>0
Термодинамическая
система
Q<0
Т/Д система (ТДС):
Обмен энергией E
с окружающей средой в
виде Q и W
Обмен веществом m
Окружающая
среда
W>0
Передача
теплоты - Q
Совершение
работы - W
•изолированные
•закрытые
•открытые
m=0; E=0
m=0; E 0
m 0; E 0
4.
Термодинамическая система.От свойств и состояния её образующих физических.тел:
Гомогенная (однофазная)
Гетерогенная (многофазная)
фаза 1
фаза 2
граница
раздела фаз
Фаза:
совокупность частей системы с одинаковыми физико- химическими
свойствами. Отделена от другой фазы поверхностью раздела (граница
раздела фаз)
5.
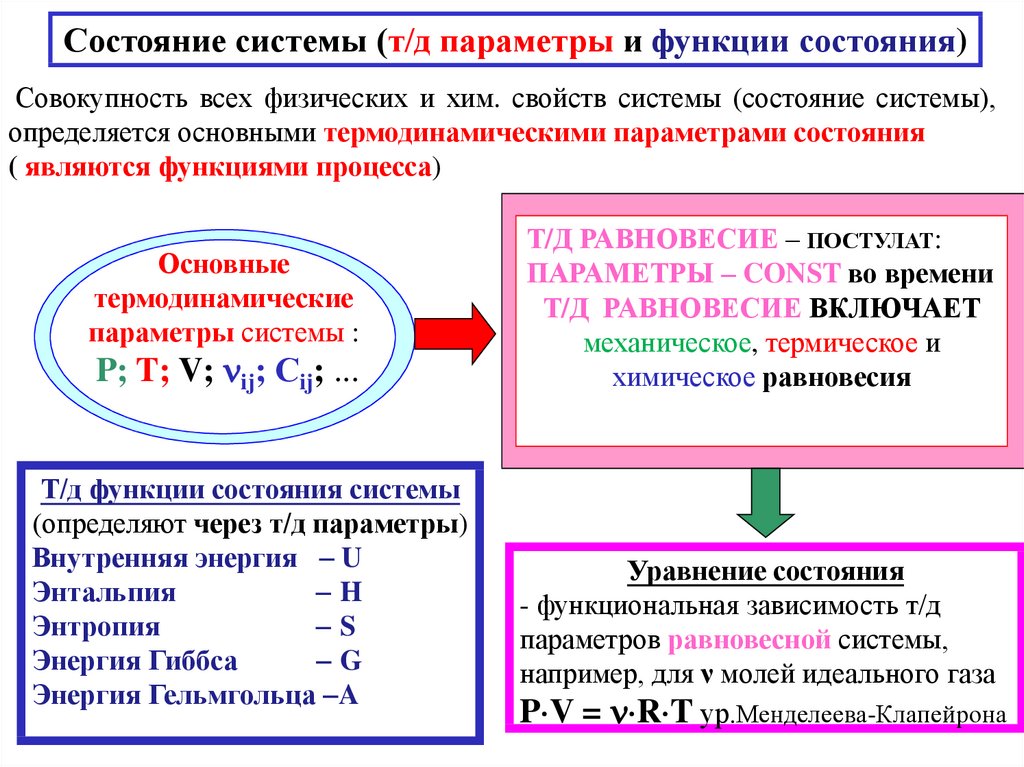
Состояние системы (т/д параметры и функции состояния)Совокупность всех физических и хим. свойств системы (состояние системы),
определяется основными термодинамическими параметрами состояния
( являются функциями процесса)
Основные
термодинамические
параметры системы :
P; T; V; ij; Сij; ...
Т/д функции состояния системы
(определяют через т/д параметры)
Внутренняя энергия U
Энтальпия
H
Энтропия
S
Энергия Гиббса
G
Энергия Гельмгольца A
Т/Д РАВНОВЕСИЕ – ПОСТУЛАТ:
ПАРАМЕТРЫ – CONST во времени
Т/Д РАВНОВЕСИЕ ВКЛЮЧАЕТ
механическое, термическое и
химическое равновесия
Уравнение состояния
- функциональная зависимость т/д
параметров равновесной системы,
например, для ν молей идеального газа
P V = R T ур.Менделеева-Клапейрона
6.
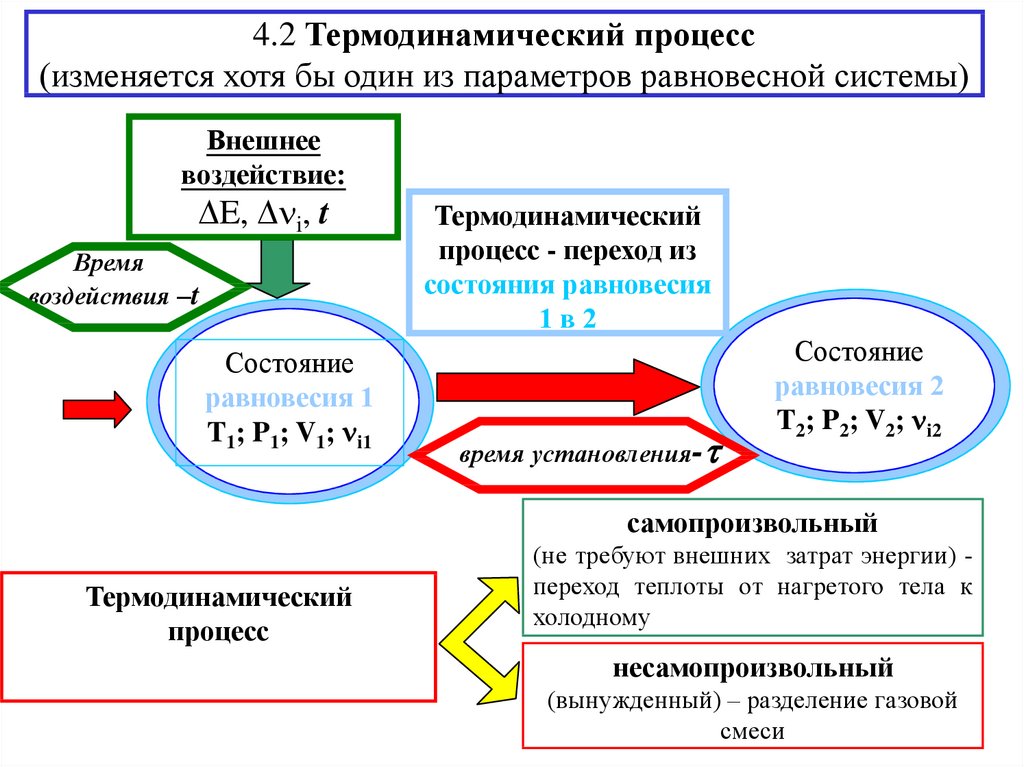
4.2 Термодинамический процесс(изменяется хотя бы один из параметров равновесной системы)
Внешнее
воздействие:
E, i, t
Время
воздействия –t
Состояние
равновесия 1
T1; P1; V1; i1
Термодинамический
процесс - переход из
состояния равновесия
1в2
время установления-
Состояние
равновесия 2
T2; P2; V2; i2
самопроизвольный
Термодинамический
процесс
(не требуют внешних затрат энергии) переход теплоты от нагретого тела к
холодному
несамопроизвольный
(вынужденный) – разделение газовой
смеси
7.
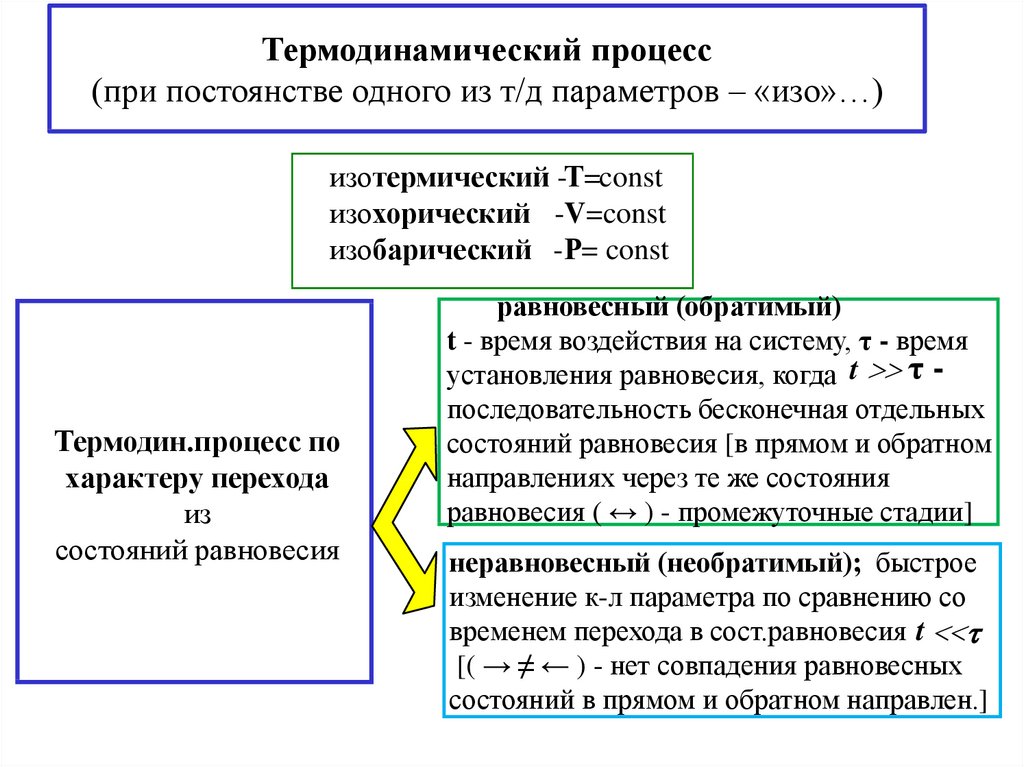
Термодинамический процесс(при постоянстве одного из т/д параметров – «изо»…)
изотермический -Т=const
изохорический -V=const
изобарический -Р= const
Термодин.процесс по
характеру перехода
из
состояний равновесия
равновесный (обратимый)
t - время воздействия на систему, τ - время
установления равновесия, когда t τ последовательность бесконечная отдельных
состояний равновесия [в прямом и обратном
направлениях через те же состояния
равновесия ( ↔ ) - промежуточные стадии]
неравновесный (необратимый); быстрое
изменение к-л параметра по сравнению со
временем перехода в сост.равновесия t
[( → ≠ ← ) - нет совпадения равновесных
состояний в прямом и обратном направлен.]
8.
Процесс изотермического расширения идеального газа(t-время воздействия на систему, τ-время перехода системы в новое
сост.равновесия)
Равновесный(обратимый) процесс
Неравновесный(необратимый) процесс
t
t
Работа W равн = W12 = W21
Р
Р1
(1)
W 12 < W равн
W 21 > W равн
T-const
Равновесие(1-2-1) P∙V = ·R·T
dW P dV R T dV
V
mg
V2
dV
W R T
V
V
P2, V2, T
1
Р2
(2)
P1, V1, T
V1
V2
V
9.
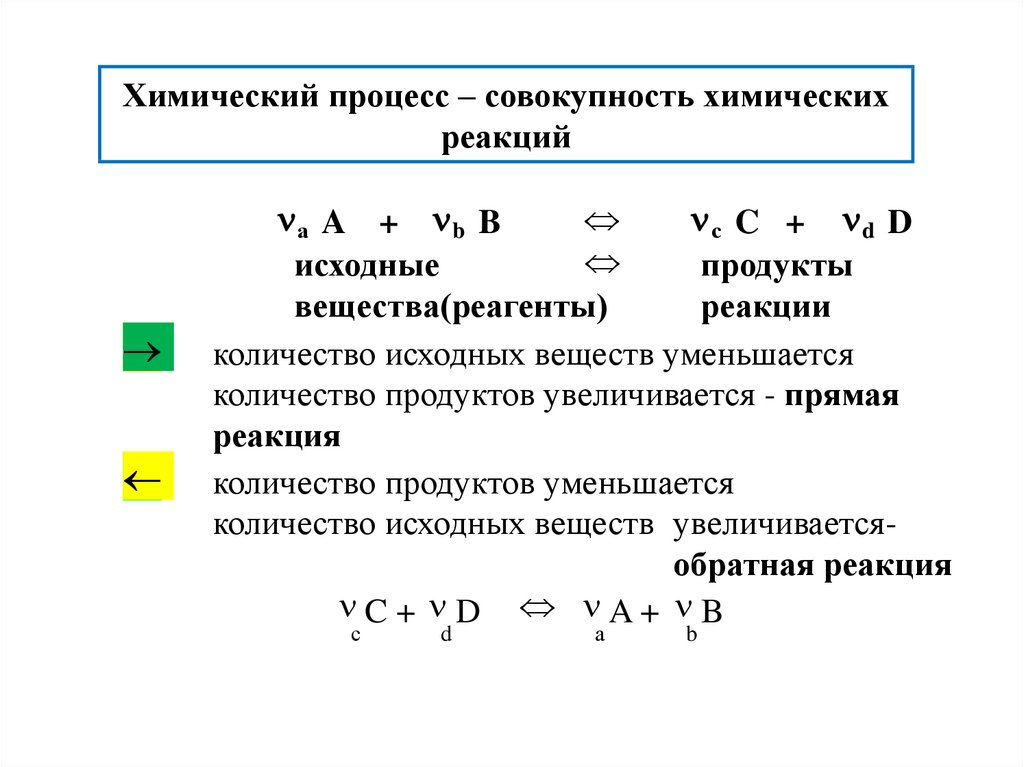
Химический процесс – совокупность химическихреакций
а A + b B
с C + d D
исходные
продукты
вещества(реагенты)
реакции
количество исходных веществ уменьшается
количество продуктов увеличивается - прямая
реакция
количество продуктов уменьшается
количество исходных веществ увеличиваетсяобратная реакция
C+ D A+ B
с
d
а
b
10.
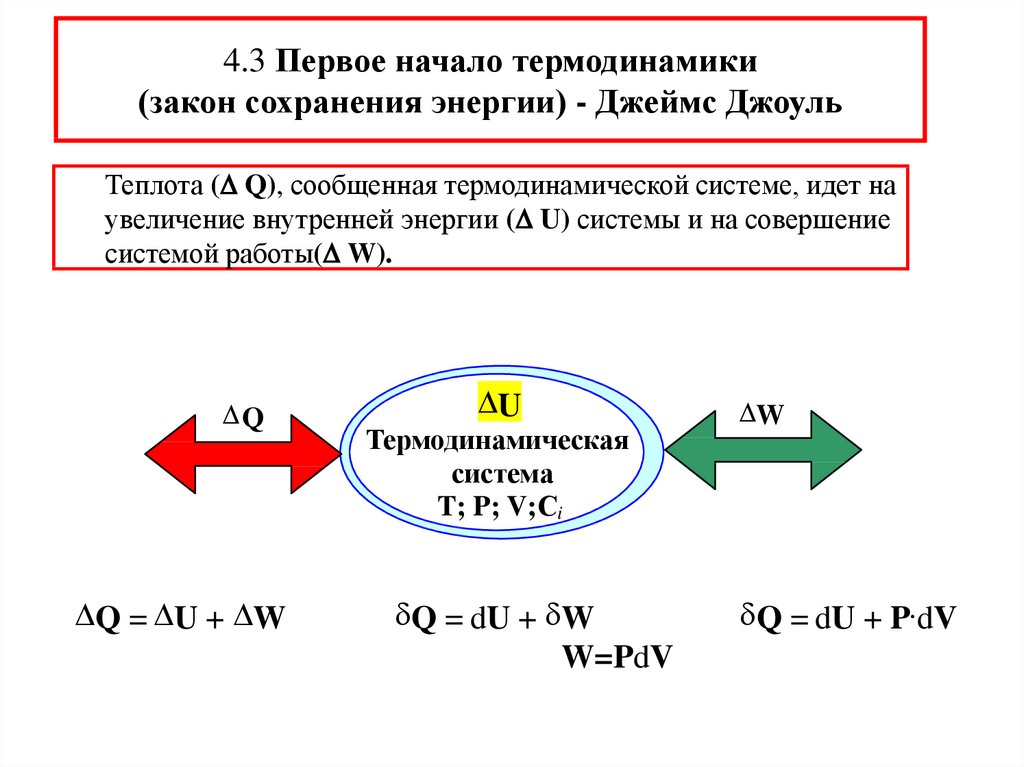
4.3 Первое начало термодинамики(закон сохранения энергии) - Джеймс Джоуль
Теплота ( Q), сообщенная термодинамической системе, идет на
увеличение внутренней энергии ( U) системы и на совершение
системой работы( W).
Q
Q = U + W
U
Термодинамическая
система
T; P; V;Сi
Q = dU + W
W=PdV
W
Q = dU + P dV
11.
Т/Д функции состоянияI. Внутренняя энергия U
U - это сумма всех видов энергии ТДС,
за исключением кинетической и потенциальной энергии системы
U [кДж]; [кДж моль], [ кДж кг]
в целом .
U функция состояния системы –не зависит
Внутренняя энергия
в химическом процессе
от пути перехода, её беск.мал. изменение –
полн. дифф-л (dU) зависит от конечн.и нач.
к
состояния
к
н
U
U
ΔU dU
U-изменение 2-х составл.
н
Химическая(Е связей)
Тепловая(кинет.Е)
для кругового процесса полное
dU 0 → изменение внутренней энергии
(как функции состояния) равно
нулю
Величину U равновесной системы характеризует Т (параметр средней
кинетич.Е частиц). Если Т2 > Т1, то UТ2 >UТ1
Термодинамическая шкала температур -Т ≥ 0 (К)
12.
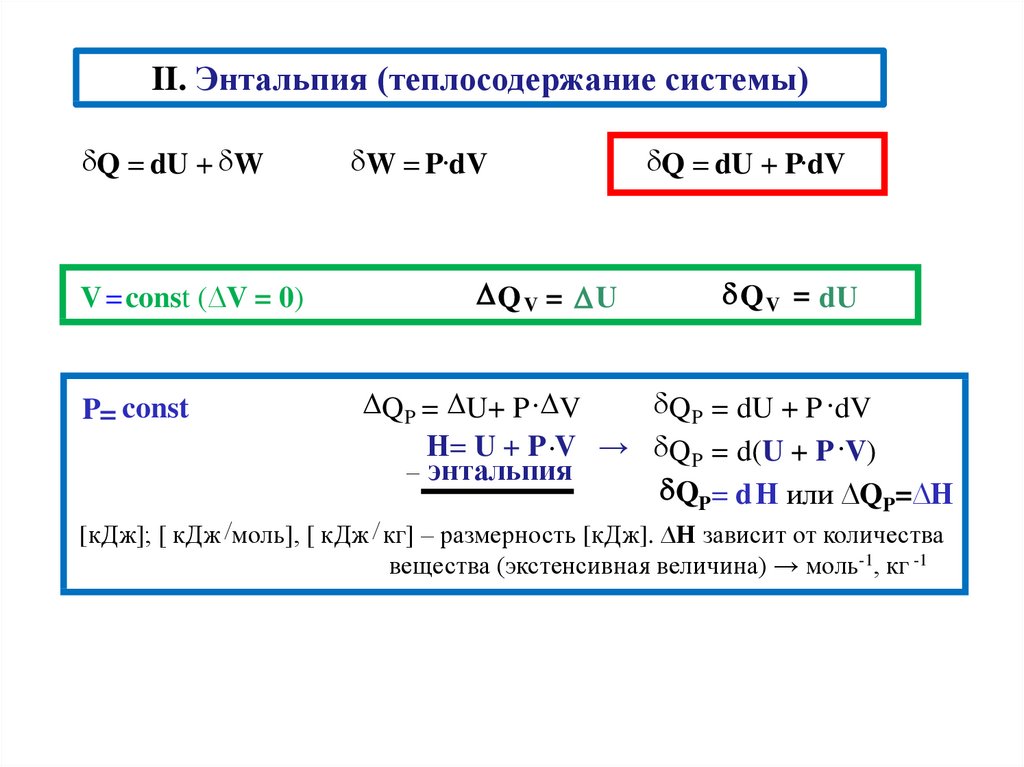
II. Энтальпия (теплосодержание системы)Q = dU + W
V =const (∆V = 0)
P= const
W = P dV
QV = U
Q = dU + P dV
Q V = dU
Q P = U+ P V
Q P = dU + P dV
Н= U + P V → Q P = d(U + P V)
– энтальпия
QP = d Н или ∆QP=∆H
[кДж]; [ кДж моль], [ кДж кг] – размерность [кДж]. ∆Н зависит от количества
вещества (экстенсивная величина) → моль-1, кг -1
13.
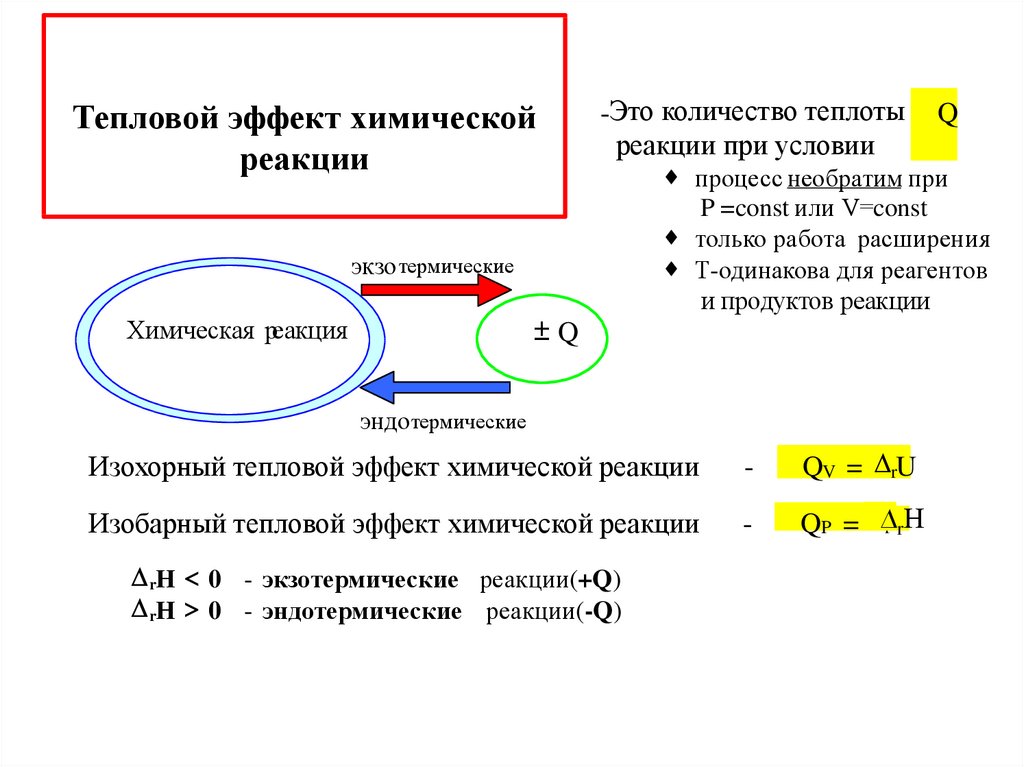
Тепловой эффект химическойреакции
-Это количество теплоты
реакции при условии
экзо термические
±Q
Химическая реакция
процесс необратим при
P =const или V=const
только работа расширения
Т-одинакова для реагентов
и продуктов реакции
эндотермические
Изохорный тепловой эффект химической реакции
-
QV = rU
Изобарный тепловой эффект химической реакции
-
QP = ∆r rН
rН 0 - экзотермические реакции(+Q)
rН 0 - эндотермические реакции(-Q)
Q
14.
Закон Гесса«тепловой эффект реакции зависит только от вида и состояния
исходных веществ и конечных продуктов и не зависит от пути
превращения одних веществ в другие (промежуточных стадий)»
rН , кДж
C; O 2
1.
2.
C + O 2 = CO 2
rН 1 = -393.51 кДж
C + 0.5O 2 = CO
rН 2 = -110.53 кДж
CO + 0.5O 2 = CO 2
rН 3 = -282.98 кДж
CO
rН 2
rН 1
rН 3
CO 2
r Н 1 = r Н 2 + rН 3
15.
Термохимические уравнения(включают тепловой эффект реакции)
4 Al + 3 O 2 = 2 Al 2O3 + r Н
rН = -3352.2 [кДж]
Превращение
одного моля
2 Al + 3 2 O2 = 1 Al 2 O3 + f Н
fН = -1676,1 [ кДж моль]
f Н - образование
одного моля в-ва
1 Al + 3 4 O2 = 1 2 Al 2O3 + cН
cН = -838,05 [кДж моль]
cН – сгорание
одного моля в-ва
16.
Стандартная (молярная) энтальпия образования(тепловой эффект образования 1 моля сложного вещества из простых в
стандартных условиях)
Термохимические расчеты (расчет тепловых эффектов реакций)
• Стандартные условия:
Р0 = 1,013 105 Па
Т0 = 298,15 К
С0 = 1моль/л
rН0298 стандартная
энтальпия(тепловой
эффект) хим.реакции
fН0298 –Стандартная энтальпия
образования веществ:
1. простые в-ва
fН0298= 0 кДж/моль
2. сложные в-ва
fН0298= - QР кДж/моль
1/2 А2 + 1/2 В2 = АВ ± fН0298
1. Газообразный водород
fН0298= 0 кДж/моль.
2. Ртуть жидкость
fН0298= 0 кДж/моль.
3.Углерод твердый
графит fН0298 = 0 кДж/моль,
алмаз fН0298 = 1,83кДж/моль
2. При сгорании сложных веществ – продукты окисления
СО2 , Н 2О, H-Hal, N2, MexOy
1.
17.
Следствие из закона Гесса:rН0298 = ( i fН0i)продукты – ( i fН0i)исходные
вещества
аA + bB = сC + dD
Для реакции
rН0298 = ( c fН0C + d fН0D ) – ( a fН0A + b fН0B)
Пример.
реакция :
fН0298, кДж/моль
CH4 (газ) + CO2 (газ) = 2 CO (газ) + 2H2 (газ)
–74,85
–393,51
–110,5
0
Расчет теплового эффекта реакции ∆Q хим.реакц :
rН0298 = [2 (–110,5) + 2 0] – [(–74,85) + (–393,51)] = 247,36 [кДж/моль]
∆Q хим.реакц. = - rН0298 ‧ υ = -247,36 [кДж], где υ=1
υ = число молей, {величина энтальпии хим.реакции rН0298 отнесена к
одному молю - [кДж/моль]}
18.
Зависимость теплового эффекта реакции от температурыcp – молярная изобарная
теплоемкость [Дж/мольК]
cр =
T
0
H
H
c
dT
298
f T
f
р
298
Q р
dT
=
dH
dT
T
0
H
H
c
dT
298
f T
f
р
298
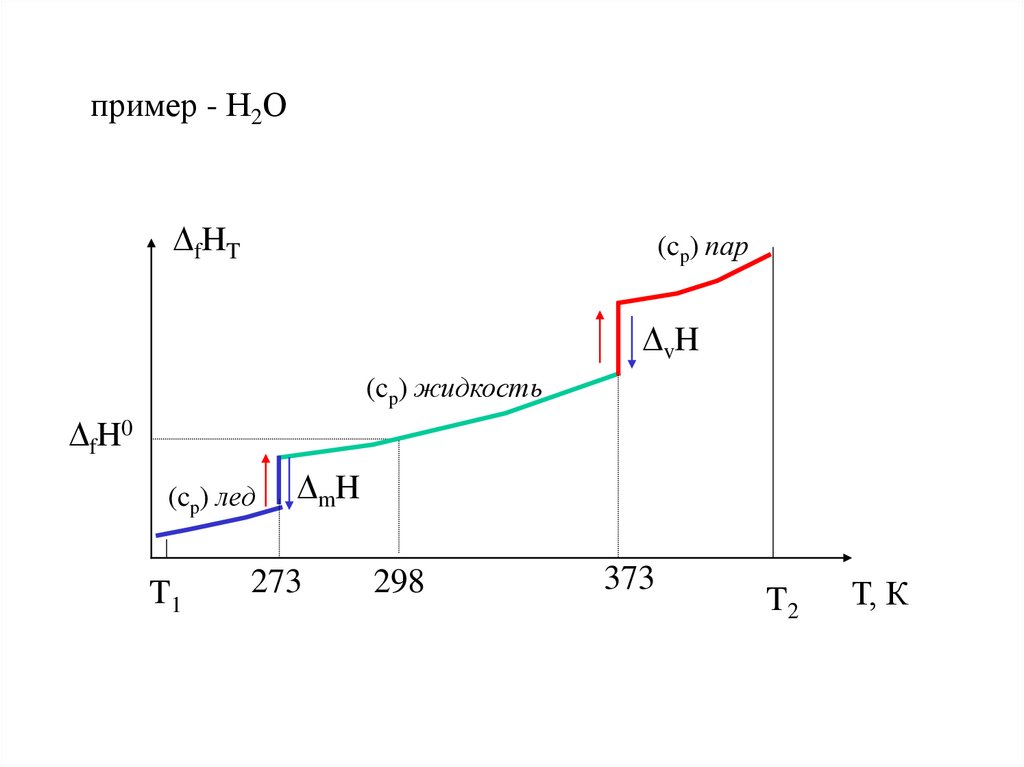
Если в интервале Т1 - Т2 фазовые переходы: плавление Тпл, кипение Ткип
Т
пл
Т
T
кип
2
0
0
T
2 T
1 рт
m
р
ж v
рп
T
Т
Т
1
пл
кип
H
H
c
dT
H
c
dT
H
c
d
mН0 [кДж/моль] – энтальпия плавления
vН0 [кДж/моль] – энтальпия испарения
ср - const
HТ2 – HТ1 = ср (T2 – T1), (∆Т - не слишком широкий интервал)
cp(Т) = а + b Т + c Т2 +…- точное значение из полиномов (справочники)
19.
пример - Н2ОfHT
(cp) пар
vH
(cp) жидкость
fH0
(cp) лед
T1
mH
273
298
373
T2
Т, К
20. Второе начало термодинамики
Q1 Q 2 T1 T2η
Q1
T1
δ Q1 δ Q 2
0 (*)
T1
T2
Q1
Q2
0, η - КПД, Q - кол-во теплоты,
T1
T2
Т - температура
Q
равн
Q
S ∆S=δQ равн/T –энтропия
0
T
T
(формула Клаузиуса,1850 г)
Если цикл Карно - сумма беск.малых циклов, в каждом из которых (*), то под
интегралом по замкнутому контуру Q/T– функция состояния, названная S
Q = dU + W
1-е начало
dS
δQравн
T
dUравн=dUнеравн Wнеравн < Wравн
dS
δQнеравн
T
dS
δQ
T
Qнеравн Qравн
T dS δQ
δQ из 1-го начала, тогда dU + p dV -TdS 0 в изолированной системе dU=dV= 0 → TdS≥0 → dS ≥ 0 (т.к.T≥0)
δQ - TdS ≤ 0;
в изолированной системе самопроизвольно протекают процессы с
увеличением энтропии (dS > 0), которые прекращаются при равновесии
(dS = 0) , когда S принимает максимальное значение – 2-ое начало т/д
21.
III. Энтропия и т/д вероятность1
W1= 1
2
W2= 4
3
W3= 6
1 – 5 варианты распределения по двум
половинам сосуда 4-х частиц(макросостояния
системы)
Wi – число способов (микросостояний)
реализации макросостояний 1-5 системы
при размещении 4-х частиц (с № 1,2,3 и 4)
ΣWi=16 - всего способов размещения в 1-5
P=6/16 математическая вероятность Max
W3=6 макс.(для выравнивания конц.)
Wi – термодинамическая вероятность
4
W4= 4
5
W5= 1
0≤P≤1
1≤W≤∞
22.
Энтропия. Уравнение БольцманаS = k lnW
k = 1,38 10-23Дж К – постоянная Больцмана (k = R/NА)
W – термодинамическая вероятность данного состояния число возможных микросостояний системы, которые обеспечивают
параметры данного макросостояния W 1
(уравнение Больцмана - связь энтропии по Клаузиусу с вероятностным
подходом, трактовкой хаотичности, как объективного качества окруж. мира)
Второе начало термодинамики. Вероятностный подход
В изолированной системе самопроизвольно идут только процессы в
которых реализуется более вероятное состояние системы, т.е. процессы
сопровождающиеся увеличением термодинамической вероятности W и
следовательно энтропии S.
Т.о. в изолированной системе для самопроизвольного процесса
изменение энтропии
ΔS>0
23.
Второе начало термодинамикиВ изолированной системе самопроизвольно будут протекать процессы с
увеличением термодинамической вероятности, а состояние равновесия
соответствует состоянию с максимальной вероятностью.
Третье начало термодинамики
(теорема В.Нернста 1906 г. и постулат М.Планка 1911 г.)
*Энтропия идеального кристалла при 0 К равна нулю. Поэтому энтропия
любого вeщества абсолютна и положительна
2-е начало т/д описывает системы:
• число частиц должно быть велико, статистически значимо(>1012-1014)
• число частиц – конечно
•не распространяется на неограниченную(бесконечную) систему [W
становится неопределенной(бесконечное число состояний)]
24.
Факторы влияющие на величину энтропииS [Дж К]
• Фазовый переход:
стандартная - S0298 [Дж моль К]
H
фп
S
S
S
ф
1
ф2
фп
T
фп
Фаза
лед
жидкая вода водяной пар
S0298, Дж моль К
39,33
69,95
188,72
• Состав, структура: O, O2, O3 - рост энтропии
• Химическая реакция:
rS0 = ( i S0i)продукты – ( i S0i)исх. вещества
• Температура: dS=δQ/T δQ=cdT dS=c dT/T
T
2
H
dT
dT
фп
S
S
(
c
)
(
c
)
Т
2
Т
1
р
1
р
2
T
T
T
фп
T
1
T
фп
T
фп
25.
IV. Энергия Гиббса (изобарно-изотермический потенциал)Направление химического процесса
T dS dU + p dV
dU + p dV -T dS 0
[см. (*) на слайде 19]
δQ - TdS ≤ 0, т.к. dS
dU + p dV - T dS < 0
- самопр. процесс
dU + p dV - T dS =0
- равновесие
δQ
T
T dS δQ
• Изобарно-изотермический процесс (p–const, Т–const)
dU + p dV - T dS 0
dH – T dS = d(H – T S) => dG 0
G H – T S - энергия Гиббса (изоб.-изотерм.пот.) [кДж; кДж моль]
rG(T) = rH(T) – T rS(T) = 0 условие термодинамического равновесия
rG(T) = rH(T) – T rS(T) < 0 условие самопроизвольного процесса
• Изохорно-изотермический процесс (V–const, Т–const)
dU - T dS = d(U – T S) = dА 0
A U – T S - энергия Гельмгольца
[кДж; кДж моль]
26.
Стандартная энергия Гиббса (образования) вещества ΔG0298Энергия Гиббса реакции
rG0298 = ( i fG0i)продукты – ( i fG0i)исходные вещества
r G r G
аA + bB = сC + dD
rG0= ( c fG0C + d fG0D) – ( a fG0A + b fG0B)
rG0298= fH0i – 298 rS0
rG0 298 = [ i ( fH0i – 298 S0i)]продукты –[ i( fH0i – 298 S0i)]исходные вещества=
= [( i fН0i)прод.–( i fН0i)исх. в.]–298 [( i S0i)прод.– ( i S0i)исх. в.] =
rG0298 = rH0 – 298 rS0
27.
Температурная зависимость rGrG(T) = rH(T) – T rS(T)
rG 0 – самопроизвольный
процесс
rG(T) rH0 – T rS0
rG(T) rH0 – T rS0 0
Вклад энтальпийного ∆Н и энтропийного
∆S факторов в зависимости от Т
Направление протекания химической реакции
rH0 0
Экзотерм.
rH0 0
Эндотерм.
rS0 0
rG 0 при любой Т
rG 0 при
rH0
T
rS0
rS0 0
rG 0 при
rH0
T
rS0
rS0 0
rG 0 при любой Т
rS0 0
28.
Энергия Гиббса реакции в нестандартных условияхреакция
аA + bB = сC + dD
rG0 = ( c fG0C + d fG0D ) – ( a fG0A + b fG0B ) С0 =1 моль/л
С С0
rGi = rG0i + R T lnCi
p
с
i
i
С
X
– безразмерная концентрация
i
i
0
0
p с
i
Xi
Сi – [ моль/л ]
i – мольная доля;
pi
– относительное парциальное давление [атм], p0 =1,013.105 Па
0
p
rG = ( c fG0C+ d fG0D ) – ( a fG0A+ b fG0B) + R T ( c lnСC+ d lnCD– a lnCA–
b lnCB)
c
d
С
С
0
C D
G
G
R
T
ln
r
r
v
v
a
b
С
С
A B
v
v
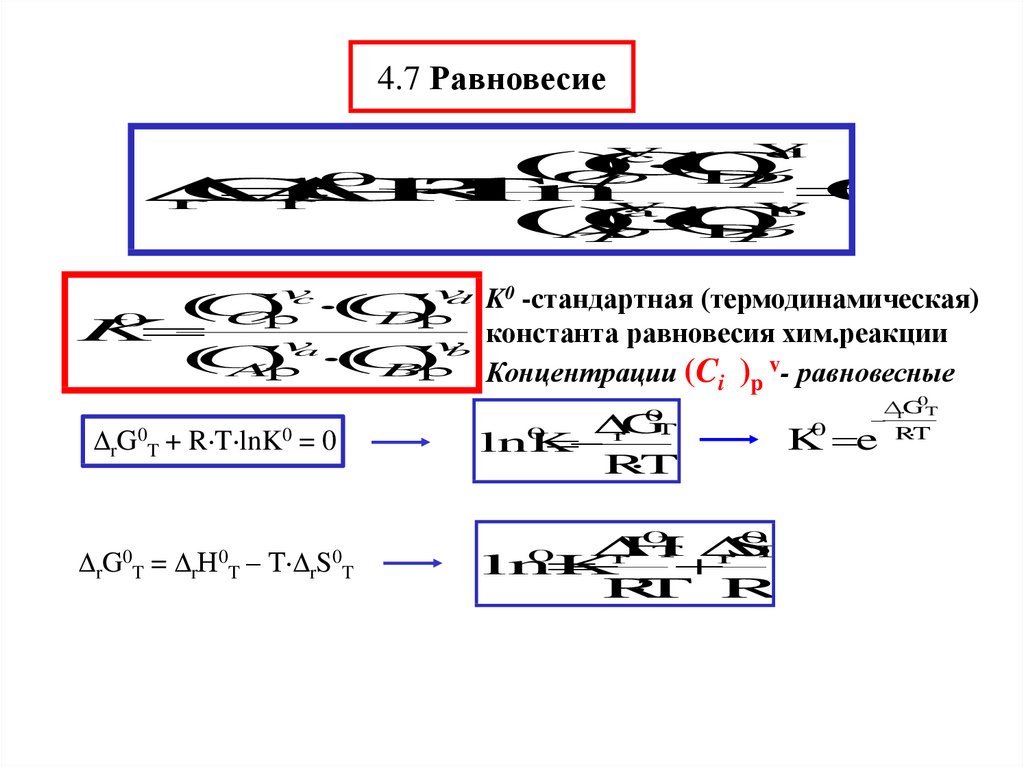
29.
4.7 Равновесиеv
d
c
(С
)
(
С
)
C
р
D
р
0
G
G
R
T
ln
0
r
r
v
v
a
b
(С
)
(
С
)
A
р
B
р
v
v
v
c
d K0 -cтандартная (термодинамическая)
(
С
)
(
С
)
Cр
D
р
0
K
константа равновесия хим.реакции
v
v
a
b
(
С
)
(
С
)
A
р
B
р
Концентрации (C ) v- равновесные
i
G
0
lnK
r
R
T
0
Т
rG0T + R T lnK0 = 0
r
G0
T
= r
Н0
T
– Т r
S0
p
0
0
H
S
Т
Т
lnK
r
r
R
T R
0
T
G0T
r
R T
K0 e
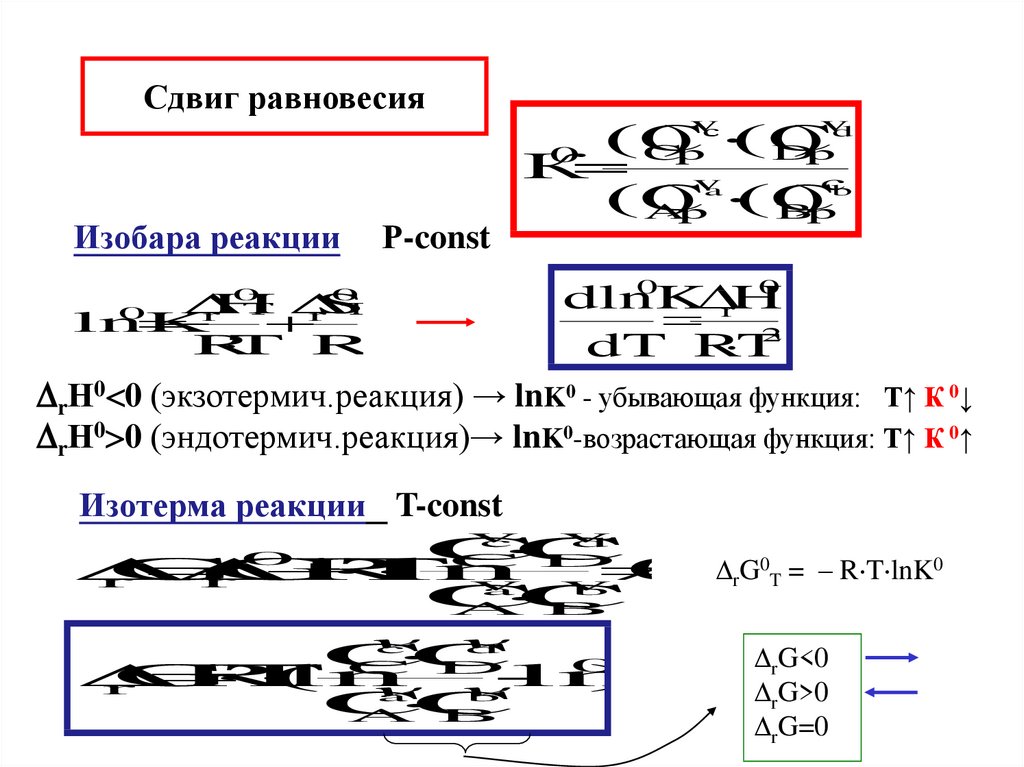
30.
Сдвиг равновесияс
d
(С
)
(С
)
Cр
Dр
0
К
v
c
a
b
(С
)
(С
)
Aр
Bр
v
Изобара реакции
Р-const
0
0
dlnK
H
r 2
dT R
T
H
S
0
lnK
R
T R
0
r Т
v
0
r Т
rН0 0 (экзотермич.реакция) → lnK0 - убывающая функция: Т↑ К 0↓
rН0 0 (эндотермич.реакция)→ lnK0-возрастающая функция: Т↑ К 0↑
Изотерма реакции T-const
c
d
С
С
0
C
D
rG0T = – R T lnK0
G
G
R
T
ln
0
r
r
v
v
a
b
С
С
A B
v
v
c
d
С
С
rG<0
0
C D
G
R
T
(
ln
lnK
)
r
rG>0
a
b
С
С
A B
rG=0



















 chemistry
chemistry








