Обобщенная линейная модель множественной регрессии с гетероскедастичными остатками. Лекция 8

1.

Обобщенная линейная модель
множественной регрессии с
гетероскедастичными остатками

2.

Слайд №1
Линейная модель множественной регрессии
Y X ,
для которой нарушено 4 условие Гаусса-Маркова называется
обобщенной линейной моделью множественной регрессии
(ОЛММР) с гетероскедастичными остатками, а именно:
1) х1,…,хк – детерминированные переменные;
2) ранг матрицы Х равен "к+1" – среди признаков нет линейно
зависимых;
3) M i 0 , i 1, n - нет систематических ошибок в измерении у;
4) D i M i2 i 2 , i 1, n
5) cov( i , j ) M ( i j ) 0 , i j , i 1, n j 1, n
T
4') M 2 0
( i2 2j , есть хотя две различные
дисперсии), т.е. на диагонали стоят неравные дисперсии, а вне
диагональные элементы равны 0.

3.

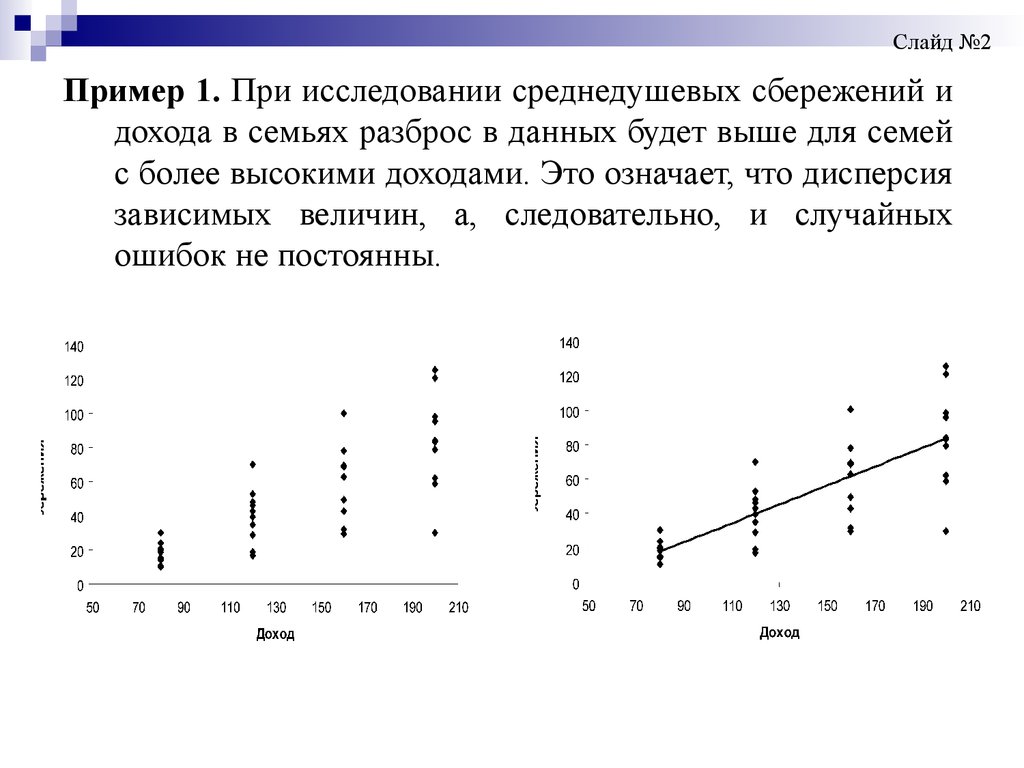
Слайд №2
Пример 1. При исследовании среднедушевых сбережений и
дохода в семьях разброс в данных будет выше для семей
с более высокими доходами. Это означает, что дисперсия
зависимых величин, а, следовательно, и случайных
ошибок не постоянны.

4.

Слайд №3
Пример 2. При изучении влияния ВВП на затраты на образование по
статистическим данным странам мира разброс значений относительно
функции регрессии выше у стран с более высокими значениями ВВП

5. Тесты для проверки гетероскедастичности Тест ранговой корреляции Спирмена

Слайд №4
Тесты для проверки гетероскедастичности
Тест ранговой корреляции Спирмена
1. Вычисляется коэффициент ранговой
корреляции Спирмена
где di — разность между рангами значений хi и ei

6.

Продолжение слайд №4
2. Выдвигается гипотеза
H 0 : xe 0
H 1 : xe 0
3. Гипотезе проверяется на основе статистика
| t |
| x ,e | n 2
1 x ,e
St n 2 / H 0

7.

Слайд №5
Тесты для проверки на гетероскедастичность
Тест Голдфелда—Квандта
1. Все n наблюдений X и Y упорядочиваются по объясняющей
переменной, влиянием которой порождается
гетероскедастичность;
2. Оцениваются коэффициенты уравнений регрессии для
первых n’ и последних n’’ наблюдений, причем
3
n' n' ' n
8
3. Выдвигаются гипотезы
H 0 : 12 22 n2 (нет гетероскедастичности)
H1 : i j : i2 2j (есть гетероскедастичность)
4. Вычисляются суммы квадратов отклонений для первых n’ и
последних n’’ наблюдений Q ' e ' T e '
T
Q ' ' e ' ' e ' '

8.

Продолжение слайд №5
Тест Голдфелда—Квандта
5. Строится статистики
6. В случае отклонения нулевой гипотезы структура матрицы
Σ0 имеет вид
Если Q2<Q1
Если Q2>Q1
x
0
0
0
0
2
1j
0
x22 j
0
0
0
0 0
... 0
0 xnj2
0
или
1
2
x1 j
0
0
0
0
0
0
1
x22 j
0
...
0
0
0
0
0
0
1
xnj2

9.

Слайд №6
Тесты для проверки гетероскедастичности
Тест Глейзера
1. Будем предполагать, что
2. Выдвигается гипотеза
H 0 :
- нет гетероскедастичности
3. Варьируя γ оценивают уравнения регрессии. Если при
оценивании значимым оказывается более одного уравнения, то
выбирают
уравнение
с
наибольшим
коэффициентом
детерминации

10.

Продолжение слайда №6
Тест Глейзера
4. В случае отклонения нулевой гипотезы структура матрицы
Σ0 имеет вид
( x1 j ) 2
0
0
0
0
0
0
0
2
( x2 j ) 0
0
0
...
0
0
0 ( xnj ) 2

11. Тесты для проверки гетероскедастичности Тест Парка (идея)

Слайд №7
Тесты для проверки гетероскедастичности
Тест Парка (идея)

12. Тест Парка (алгоритм)

Продолжение слайда №7
Тест Парка (алгоритм)

13. Тест Бройша-Пагана-Годфри (идея)

Слайд №8
Тест Бройша-Пагана-Годфри (идея)

14. Тест Бройша-Пагана-Годфри (алгоритм)

Продолжение слайд №8
Тест Бройша-Пагана-Годфри
(алгоритм)

15. Общий тест гетероскедастичности Уайта (алгоритм)

Слайд №9
Общий тест гетероскедастичности Уайта
(алгоритм)

16.

Слайд №10
1. Стандартные ошибки в форме Уайта.
Предположим, что матрица ковариаций регрессионных остатков –
диагональная. Тогда поскольку b MHK (X T X) 1 X T , то
1
ˆ b M ( X T X ) 1 X T T X ( X T X ) 1 ( X T X ) 1 X T ˆ X ( X T X ) 1 n( X T X ) 1 ( X T X )( X T X ) 1
n
Рассмотрим матрицу
через
X (1 k ) T
S
X X .
T
Имеем ( X
T
n
X )ij= x si s2 x sj2 .
Обозначим
s 1
векторы-строки Х. Тогда
n
X X = s2 x s x Ts .
T
Уайт
s 1
показал, что
ˆ b n( X T X ) 1 ( 1 e s2 x s x sT )( X T X ) 1
n
является состоятельной оценкой
ковариационной матрицы коэффициентов регрессии. Стандартные
ошибки, рассчитанные по данной формуле называются
стандартными ошибками в форме Уайта.

17.

Слайд №11
2. Стандартные ошибки в форме Невье-Веста.
Для более сложного случая, когда в ковариационной матрице
регрессионных остатков неизвестные элементы стоят не только на
главной диагонали, но и на соседних диагоналях, отстоящих от
главной не более, чем на L (т.е. ij 0, i j L . Невье и Вест показали,
что оценка
L
n
ˆ b n( X T X ) 1 ( 1 es2 x s x sT 1 j et et j ( xt x T t j xt j xt )( X T X ) 1
n
n j 1 t j 1
явяляется
состоятельной оценкой ковариационной матрицы коэффициентов
регрессии.
Существует несколько способов выбора весовых коэффициентов
j :
- наиболее простым j =1. Однако при таком выборе матрица
может оказаться неположительно-определенной.
- j =1- j (Бартлетт).
L 1
3
-
j =
L 1
j 2
j
1 6(
) 6
,1 j
L 1
2
L 1
j 2 L 1
2(1
) ,
j L
L 1
2
(Парзен).